多行程带补货时间窗的成品油多舱配送路径优化

王旭坪，詹红鑫，孙自来，李芳芳

多行程带补货时间窗的成品油多舱配送路径优化

王旭坪1,2，詹红鑫1，孙自来1，李芳芳3

（1.大连理工大学 系统工程研究所, 辽宁 大连 116023；2.大连理工大学 商学院, 辽宁 盘锦 124221； 3.长江师范学院 管理学院, 重庆 408100）

本文以多行程带补货时间窗的成品油二次配送路径规划为研究对象，以运输成本和派车成本之和最小为优化目标，研究多舱位、多行程、多车型、硬时间窗的车辆路径问题模型。基于先行程后分组的求解策略对问题进行划分，并引入行程池的概念，设计了包含内外两层循环的启发式算法。最后，通过多组仿真算例验证了上述模型和算法的有效性，并通过数据实验揭示了以下规律：（1）当加油站补货时间窗分布均匀时，车辆周转次数和时间利用率相对较高；分布集中时，车辆周转次数较低且派车量增加；有效的交通管制时间设置，不仅能降低配送成本，还可提高车辆利用率。（2）相对于舱位配载类型固定的车辆配置，配载类型不固定的车辆配置在运输成本和车载率上具有优越性；但当现有车舱配载方案接近或达到当前配送需求的最优配置时，配载类型固定的车辆配置在总成本上具有明显优势。

成品油二次配送; 补货时间窗; 多行程; 多舱位; 路径优化

0 引言

成品油二次配送（以下简称“配送”）位于油品供应链的末端，泛指通过油罐车将成品油从油库配送到各加油站和社会客户的过程，是提高油品配送效率，降低物流成本的关键环节。有别于传统的被动要油模式，近年来，国内成品油销售公司逐渐引入主动配送策略，对附属加油站的油品存储和配送进行主动管理；通过先进的物联网技术，配送中心能够实时监控并预测加油站各种油品的库存和销售情况，同时生成配送订单对加油站进行油品补给。因此，如何实现成品油配送计划的统一管理、运力资源的统一调度、降低运输成本和提高配送效率已成为成品油配送管理的核心问题。

成品油配送是车辆路径问题（Vehicle Routing Problem, VRP）在油品运输领域的典型应用，除了具有传统VRP问题的复杂性（多车型、多产品等）之外，还具有如下油品配送特性：

（1）车辆多舱：成品油配送车辆多为分舱油罐车，可同时装载不同型号的油品为多个加油站进行配送。且除非油罐车经过清洗操作（此时舱位装载类型不固定），否则每个舱位的油品装载类型固定，即不同类型油品严禁混装。

（2）满舱配载：成品油属于易燃易爆的危险品，在非满载情况下，液体与罐壁的摩擦容易引发车辆事故，且晃动的液体不利于车辆的稳定行驶，因此成品油配送需要满足满舱配载约束。同时，出于配送管理的需要，每个舱位单次配送只能满足单个加油站单种油品的需求，因此加油站的油品需求量为可用舱位载重的整数倍。

（3）补货时间窗：不同于传统VRP问题的客户服务时间窗，由于加油站的每一种油品均有独立的存储地罐和监测设备，因此即使是同一加油站，每种油品的补货时间窗也不近相同；因此，可能需要车辆在满足不同油品补货时间窗的情况下对同一加油站进行多次配送。

（4）多行程配送：由于满舱配载和加油站多油品的要求，油罐车单次配送的规模较小，同一油罐车需要执行多个行程的配送任务。当前国内成品油配送普遍存在调度不合理的现象，单周期内的平均周转次数仅为2次，车辆利用率较低。

所以成品油配送需要综合考虑舱位配载类型指派、多行程构造、多行程分配等问题，其求解难度远大于一般车辆路径问题。同时，据中石油报道，在现有的成品油物流体系中，公路配送成本占总物流成本的比重高达60%~70%。研究成品油多舱配送问题，制定经济高效的配送方案，具有重要的理论和实际意义。

针对成品油二次配送路径优化问题，国内外学者分别结合不同的配送情景和配送策略展开了研究。国内最早由宋洁蔚等对该问题进行了研究，他们根据加油站的库存情况和配送网络结构，对加油站的油品需求量和配送时间窗进行分析，设计了一种可便捷求解的启发式算法[1]；熊静进研究了非满载情况下的成品油调度问题，设计了鲁棒性较强的禁忌搜索算法和遗传算法，并结合武钢交运集团的加油站配送业务，开发了成品油配送管理的计算机系统原型[2]；孙丽君采用情景建模的方式分析了成品油配送干扰管理问题，通过决策情景的分析，获取了关键情景要素及其相互间的关系，并构建了决策情景的表示模型，为成品油调度的实时建模奠定了基础[3]。李敏等引入了订单邻域的概念，将成品油多舱配送订单的时间、空间和油品类别进行综合度量，通过聚类的方式构建订单邻域系统，并结合改进的量子遗传算法对所构建的成品油多舱配送模型进行求解[4]。近期，张源凯等建立了多车型多车舱的车辆优化调度模型，提出基于C-W节约算法的“需求拆分→合并装载”的车辆装载策略，并利用Relocate和Exchange算子进行并行邻域搜索[5]。张立峰等引入了油罐车的最远分载距离约束，研究了大规模多车场带时间窗的成品油配送问题，并提出了“期望节约里程”指标用于指导遗传算法的搜索[6]。

在国外相关研究中，成品油配送路径优化问题也被称为加油站补货问题。Fabien Cornillier等一直致力于该问题的研究，并针对带时间窗约束、多油库配送、多周期配送等情景，分别设计了高效的求解算法，并通过真实算例，验证算法的有效性[7-10]。此外，针对多周期的加油站配送问题，Vidović等提出了可以求解小规模配送问题（3个配送周期，10个待配送加油站）的整数规划算法，设计了可求解50个加油站，5个配送周期的启发式算法[11]。而Popović等在考虑多周期配送的同时，引入了库存优化变量，设计了求解的变邻域搜索算法，最终输出结果包括油品的配送类别和配送量，以及具体的配送方案[12]。

综上所述，目前国内外学者主要从多车型、多周期、库存-路径联合配送等方面对成品油多舱配送问题进行研究，较少考虑多行程、多补货时间窗以及舱位配载类型约束等实际因素的影响。本文在已有研究的基础上，对固定车辆数和补货时间窗约束下的多车型、多车舱、多行程的成品油配送路径优化问题（Multi-Compartment Multi-trips Vehicle Routing Problem with Time Windows，MCMTVRPTW）展开研究；设计了求解的启发式算法，该算法借鉴了Christian Prins等[13]提出的先行程后分组的求解策略，利用最大评价因子顺序插入法及大邻域算子分别进行行程的构建和优化，采用贪婪策略完成舱位配载类型的指派以及行程的分配。最后，根据成品油配送实际情况构造算例，验证了算法的有效性，并进一步通过数据实验分析了多种情景下成品油多舱配送的特点，为配送中心的调度提供决策建议。

1 问题描述及模型构建

1.1 问题描述

为便于模型的构建和问题的求解，本文有如下说明及假设：

（1）任意订单的油品需求量均不超过可用车型的最大舱位，且由于成品油配送具有明显时效性，本文只讨论补货时间窗为严格硬时间窗的情形，即配送时间超过时间窗要求，就会造成配送失败。

（2）忽略油罐车的装油时间，在执行多个行程的间隙，允许在油库停留，且油库无服务时间限制，初始时刻设为0；

（3）同一行程不允许重复访问相同加油站，即无加油站访问回路，因此，当任意行程包含同一加油站的多种油品订单时，上述订单必须在满足各自补货时间窗约束的前提下被连续服务。

1.2 模型构建

结合上述参数和变量定义，本文构造的成品油配送模型如下：

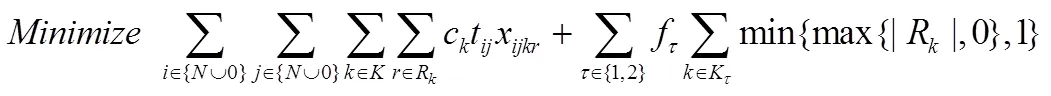
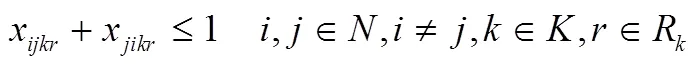
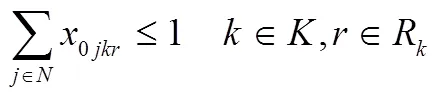
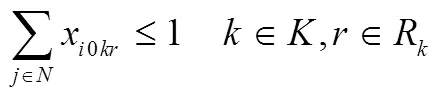
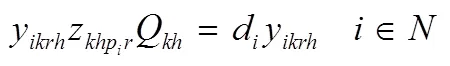
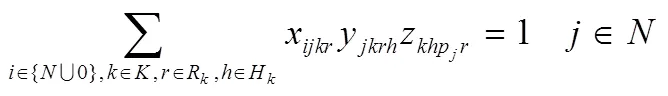
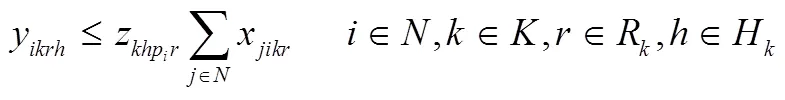
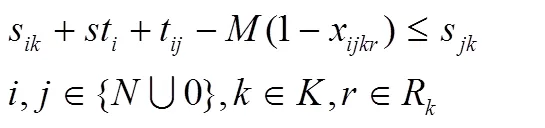
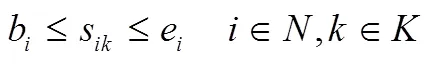
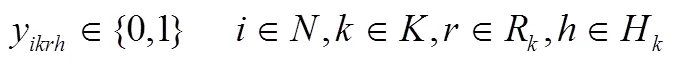
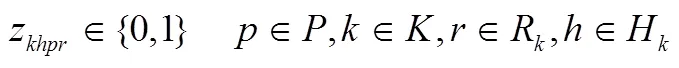
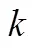
2 算法整体设计

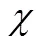
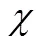
：初始化行程池AMR和其他算法参数；

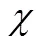
3 MCVRPTW问题可行解的构造与优化

3.1 顺序插入法

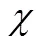
3.1.1 插入有效性检测

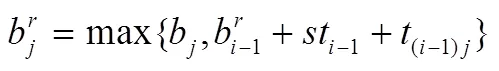
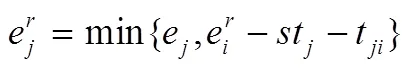
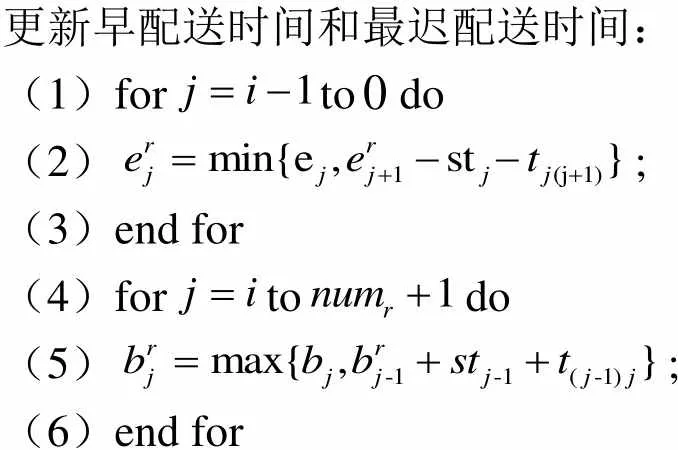
更新早配送时间和最迟配送时间： （1）fortodo（2）;（3）end for（4）fortodo（5）;（6）end for

3.1.2 评价因子

其中：

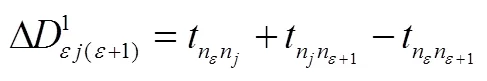
3.1.3 最大评价因子顺序插入法

结合模型特点，本文定义种子订单的选取遵循以下两条规则：

种子订单的选取兼顾了订单补货服务的紧急性以及待配送加油站的距离，并按二者的优先级得到了上述两种规则。本文采用轮换交替的方式使用这两个规则。

最大评价因子顺序插入算法的总体步骤如下：

3.2 大邻域算子

3.2.1 行程拆分

3.2.2 行程重组

（3）分别计算各行程中访问加油站节点构成的重心坐标，并按求解TSP问题的贪婪策略，将所有行程根据各自重心的位置连接成为一条完整的访问序列。

3.2.3 序列分割

4 MAPLV问题的求解与优化

4.1 MCVRPTW可行解的接受规则

4.2 行程分配算子

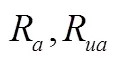
4.3 舱位配载类型指派

4.4 MAPLV问题解的评价

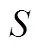
4.5 MAPLV问题解的后优化

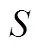
4.5.1 局部优化算子

基于尽可能不破坏原有行程结构的原则，本文以单位行程为操作对象，定义三种局部优化算子，即重定位算子、交换算子以及插入算子。

（1）重定位算子（Relocate）：任意选取一个行程，将其从当前车辆的配送计划中移除，并插入到同一配送计划的其他位置；

（2）交换算子（Swap）：随机选取两个位于不同车辆配送计划的行程，并交换对应位置；

（3）插入算子（Insert）：与重定位算子类似，仅将被选行程插入不同车辆的配送计划中。

规则2：优先选择所在配送计划包含较少行程数的行程运用插入算子，将其插入至其他配送计划中；

规则4：优先对车辆运行时间接近上限的配送计划，采用重定位算子和交换算子；

为了加强整体优化效果，上述规则与随机规则一起采用交替使用的方式进行。

4.5.2 重排序算子

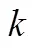
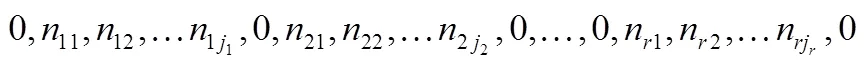
（1）上浮操作（Shift_up）：随机选择一个订单，并将其与对应的父节点交换位置；

（2）下沉操作（Shift_down）：随机选择一个订单，并随机与其左右子节点交换位置；

重排序算子中，非首尾端点处的油库节点0也参与交换操作，且当有多个0节点相连时，将其合并为一个，即进行油库节点的删除操作。因此，将油库节点引入上述交换操作中，能够起到减少行程数目的作用。

5 行程池的更新及行程选择算子

5.1 行程池的更新

5.2 行程选择算子

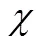
：若AMR不为空，则转Step2；否则转Step6；

6 求解算法的整体描述

综上所述，MCMTVRPTW问题求解的流程伪代码如下：

7 算例分析

7.1 算例设置

目前关于成品油多舱配送的研究较少，且实际数据获取难度较大。因此本文分别参考中石油大连市旅顺配送区（以台山油库为配送分站，负责辖区20座加油站配送），东部配送区（以庄河油库为配送分站，负责辖区26座加油站配送）以及北部配送区（以瓦房店油库为配送分站，负责辖区56座加油站配送）的配送规模和站点分布规律，仿真生成三组分别包含20，26和56个加油站的坐标数据集，定义为区域0（A0）、区域1（A1）和区域2（A2），分别如图1所示，可知油库远离市区，且所有加油站分布具有中心区域分布密集、远郊区分布稀疏的规律。

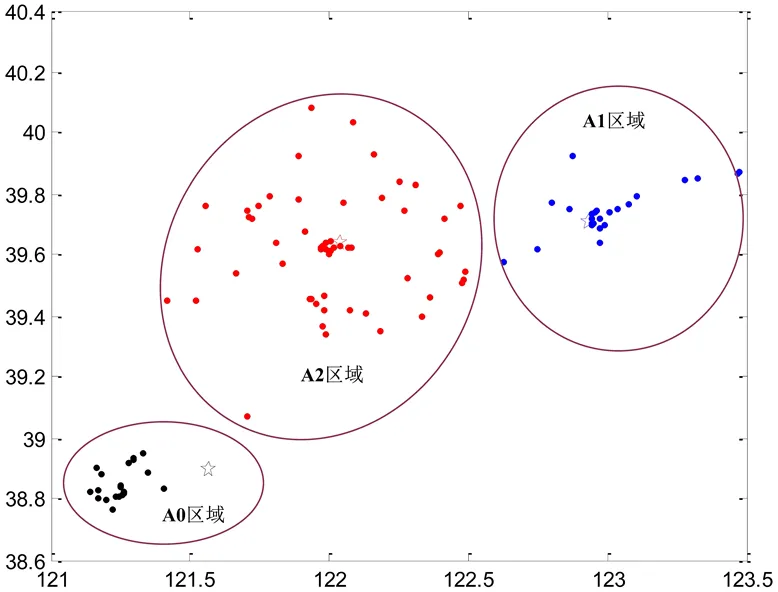
图1 加油站布局情况

Figure 1 Distribution of gas stations

本文定义4种类型的补货时间窗分布，即聚集分布（Clustered，C）、均匀分布（Uniform，U）、管制分布（Traffic Control，TC）以及随机分布（Random，R）。其中，管制分布的出现是由于成品油配送属于危险品运输，而在某些城市配送中，其补货时间窗会根据交通管制要求做出相应调整，例如沈阳市规定：青年大街昼夜禁止货车通行；而关系民生的槽罐车可以在规定时间限时进入限行区域行驶。管制分布类似于聚集分布，不同之处在于管制分布要求管制区域加油站的补货时间必须在固定时间范围内，且不同管制区域的时间要求不尽相同。本文按照算例的信息进行命名，包括坐标数据集和补货时间窗分布类型，例如算例A1-R代表在区域1执行且补货时间满足随机分布的数值算例。

此外，通过访谈加油站工作人员，获得成品油配送过程中的一些实际特征，例如国内常用油罐车最多分4个舱，加油站每次需求多为2种油品，且单种油品需求量多为5t/10t，而油罐车的固定派车成本与清舱费用均按吨位进行计算。基于上述特征，设置本文所使用车型的相关参数如表1所示，其中油罐车的固定派车成本为12元/吨，而油罐车清舱费用根据市场调研设置为125元/吨；同时，K1类车辆舱位随机对应一种油品，且使用K2类车辆时需要支付额外的清舱费用。

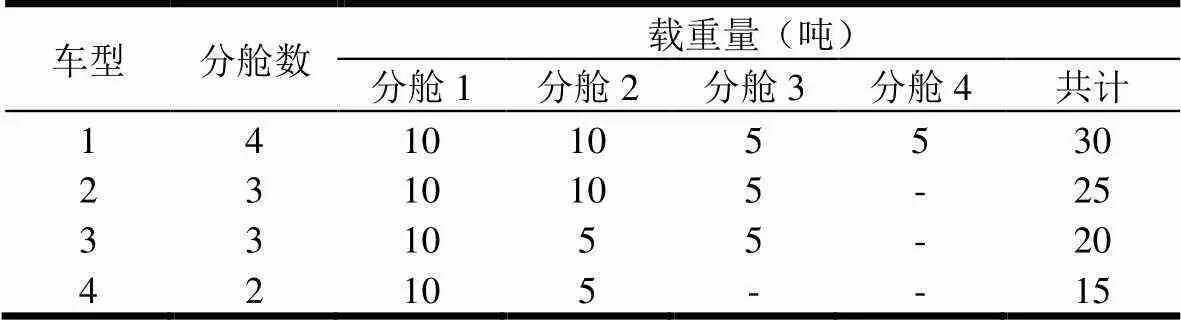
表1 油罐车车型

7.2 算法参数设置

算法通过MATALB7.0编程实现，所有程序均是在主频2.0Ghz、4GB内存、Windows7操作系统环境下运行。

下面对算法中需要预先设定的主要参数值进行说明：

图2 门槛值与目标值关系

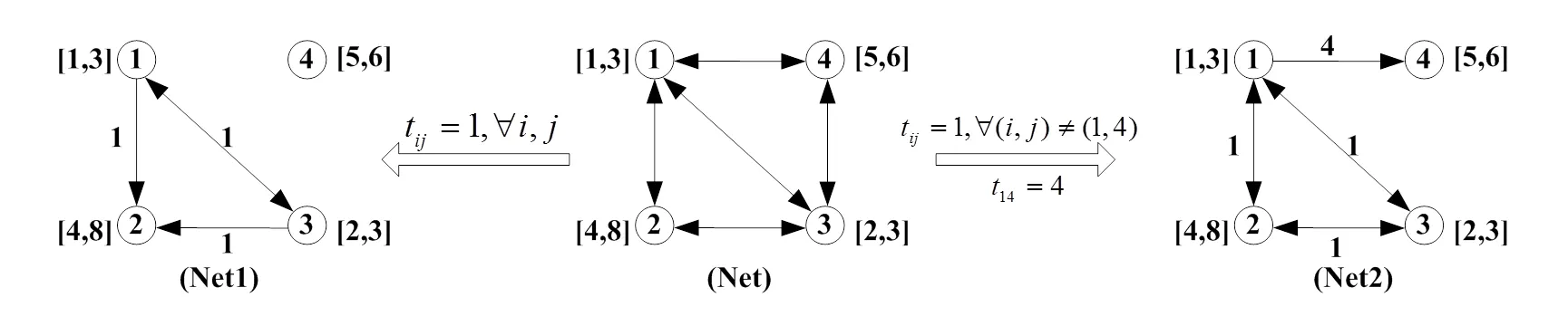
图3 运行时间对最优解的影响

Figure 3 Traveling time influences on optimal solution

7.3 算法有效性分析

为验证算法设计的有效性，我们将本文算法与另外两种算法作了对比，所有对比算法均采用相同运行参数和环境，不同之处在于，算法1采用随机插入的方式构造MCVRPTW问题的初始解；而算法2忽略了后优化过程，在调用行程分配算子对行程进行分配后，直接将其用于行程池的更新；针对每个算例和算法，重复20次独立运算，分别记录得到的MCMTVRPTW初始解目标值、优化解目标值，并计算20次运算结果的均值、标准差、最优值以及搜索到最优值的耗时。

表2为采用三种算法对算例进行求解得到的初始解和优化解的最优值，在初始解取值方面，算法1明显劣于其他两种算法，其构造的初始解取值相对于最优取值来说平均高出43.83%（最高为110.45%，最低为15.31%），表明本文设计的最大评价因子顺序插入法能够产生较为优秀的初始解；同时，12组算例中，算法2和本文算法所得的最优初始解取值接近，平均相对差仅为3.87%，且两种算法获得初始解最优取值的次数比为1:1.4，在一定程度上说明了本文算法求解结果的稳定性。在优化解取值方面，本文算法具有明显优势，相对算法1，其平均优化比率达到5.67%（最高为9.98%，最低为0.27%），说明了优秀的初始解有利于优化解的搜索；而相对算法2，其平均优化比率为6.06%（最高为11.59%，最低为2.21%），表明了本文设计的后优化算法能够有效的对可行解进行再优化，有助于优秀解的发现；此外，对比算法1和2的求解结果可发现，尽管算法2产生的初始解均优于算法1，但其部分优化解却相对较差，这一现象进一步说明了后优化过程的有效性。

表2 最优值取值情况

表3为采用三种算法对算例进行求解得到初始解和优化解最优值所对应的计算时间，在初始解运算时间方面，可以发现，算法1初始解构造所需的时间要高于其余两种算法，这主要是由于本文时间窗为硬时间窗，采用随机插入方式构造初始解时，需要进行更多的时间窗检测和装载方案检测；同时，算法2和本文算法初始解构造所花费时间的平均相对差为3.72%，且获得最优耗时的次数比为1:1.5，表明了本文算法求解时间的稳定性。而在优化解的运算耗时方面，本文算法搜索到最优解所需的时间整体高于其他两种算法，并且差距随着实例规模的扩大而增加，结合表2结果分析可知，在采用启发式方法构造初始解，并增加后优化算子之后，本文提出的求解算法能够在牺牲一定求解时间的前提下，获取到更为优秀的解。

表3 搜索到最优值的耗时

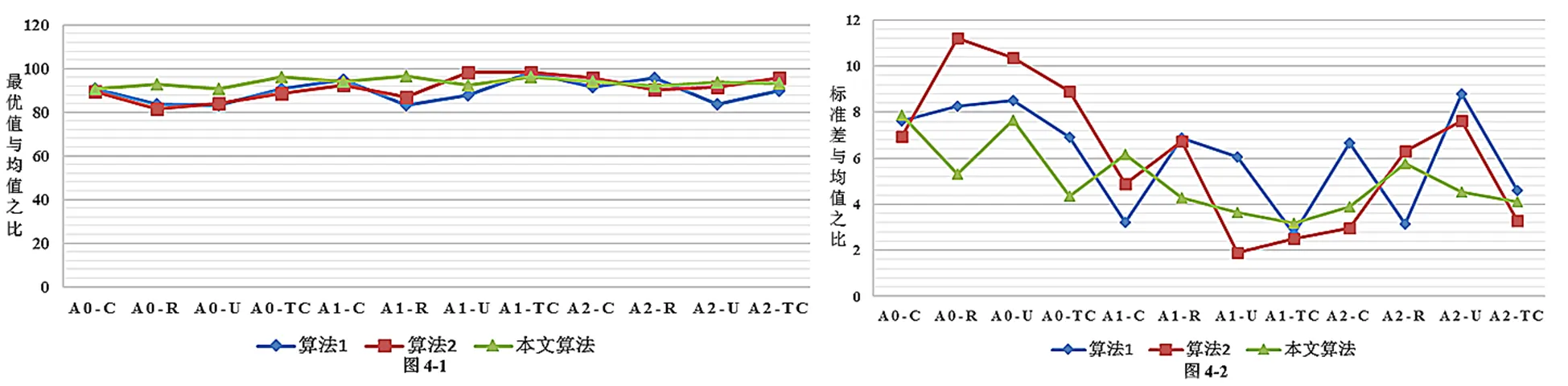
图4 相关结果取值关系

Figure 4 A series of relevant statistical indicators

为进一步证明本文算法求解的稳定性，分别记录每种算法对每个算例进行20次独立运算后所得优化解的均值和标准差，并分别计算每个算例最优值与均值的比值、标准差与均值的比值，得到结果如图4所示。由图4-1可知，相较于算法1和2，本文算法所得最优值与均值的平均差距较小（曲线较为平滑），12组算例中最优值与均值的比值控制在范围[90.62%, 96.65%]内，表明算法每次计算均能收敛到固定范围；此外，由图4-2可知，本文算法对应的曲线抖动程度相对较弱，12组算例中所得标准差与均值的比值在范围[3.19%, 7.86%]内，说明每个算例的标准差相较于平均值来说较小，即多次运算结果的离散程度不高，因此，对涉及的成品油多行程配送问题来说，本文设计的算法具有较强稳定性。

7.4 时间窗分布对调度结果的影响

为了分析时间窗分布对成品油调度结果的影响，这一节调用本文算法计算各算例在四种时间窗分布情况下的优化解，并分别记录对应的总派车数、车辆平均执行行程数（平均车辆周转率）、车辆平均执行订单数、车辆平均工作时长以及车辆平均时间利用率，其中时间利用率定义为车辆运行时长与最小时间跨度（车辆执行最后一个行程的最早完成时间与执行第一个行程的最晚发车时间之差）的比值。由于本文模型允许车辆在两个配送行程间隙在油库等待，因此车辆时间利用率取值越大，说明车辆在油库的等待时间越短，配送方案的时间利用效率就越高。

图5给出了各算例中总派车数、车辆平均执行行程数、车辆平均执行订单数三类指标的变化趋势。可以发现，在不同时间窗分布情况下，各算例指标的变化趋势大体相同；相较于其他分布类型来说，时间窗聚集分布的情况类似于油品销售旺季的配送情景，要求必须在较集中的时间范围内满足辖区加油站的所有需求，因此当时间窗跨度较小时，需要同时派出更多的车辆，并且每辆车能够执行的行程数和订单数相对较少，油罐车的周转次数较低。而对于具有管制特点的时间窗分布，其反应了现实中城市物流的管制要求，由于本文仅考虑多区域管制分布（配送区域按行政划分为多个管制区域，各区域的管制时间服从均匀分布）的情景，因此相较于其他类型，其不仅所需的车辆数较少，且每辆车所执行的行程数和订单数较高，提高了油罐车的周转次数。此外，时间窗聚集分布也可视为一类交通管制情景，即配送区域均属于同一管制区域的情景；此时需要对固定区域进行集中配送，当油罐车数量不足时，会引发加油站断油现象，对比两种管制情景下的配送方案可发现，针对不同配送区域，采用合适的管制策略，不仅能够有效的缓解城市交通压力，更能降低油品的配送成本，提高车辆周转率。

图6给出了各算例中车辆平均工作时长以及车辆平均时间利用率的变化趋势。结合图5内容可知，由于每辆车所执行的行程数和订单数较少，时间窗聚集分布算例的单车平均工作时间最短，且时间利用率最高（本文算例中均达到100%）；而针对时间窗为多区域管制分布的算例，油罐车需要在多个时间范围内执行多区域的配送任务，其单车平均工作时间会相对增加，但由于不同配送区域所在位置和管制时间存在差异，同一车辆的多个行程不一定连续，因此，其时间利用率反而较低。此外，对于需求时间分布均匀的算例来说，由于配送时间具有较高的连续性，其单车平均工作时间和车辆平均时间利用率均处于较高水平，车辆利用率较高。

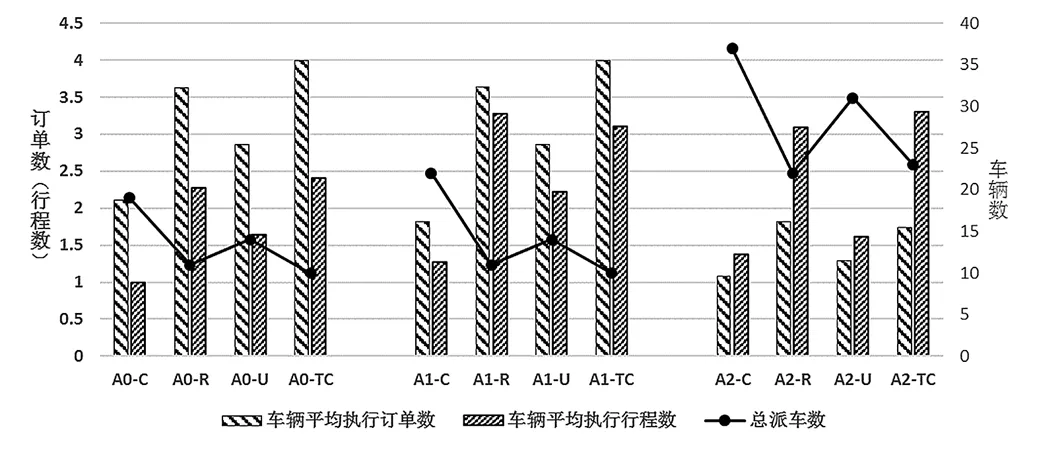
图5 三类指标的变化趋势

Figure 5 Change trend of those three indexes

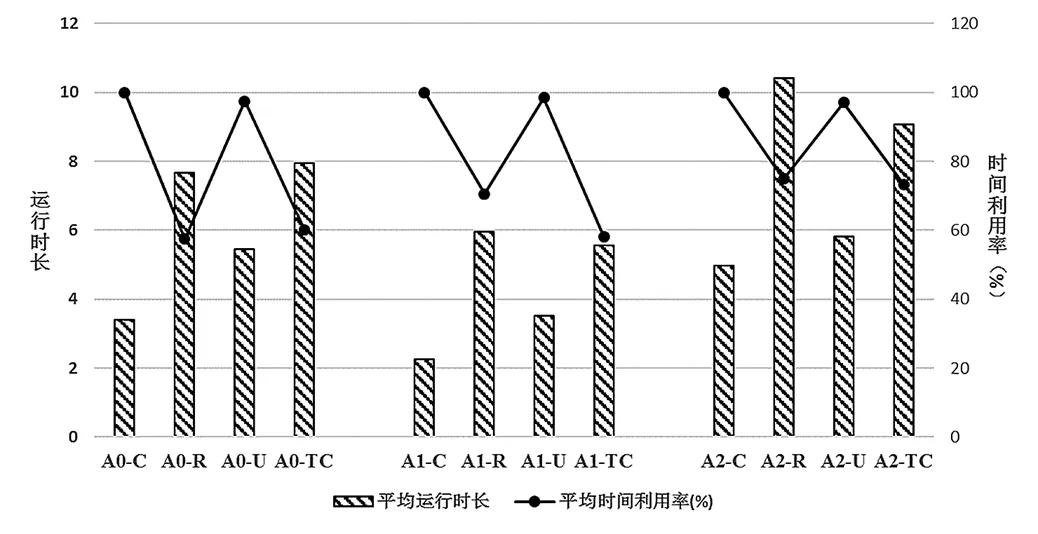
图6 两类指标的变化趋势

Figure 6 Change trend of those two indexes

7.5 车辆配置对调度结果的影响

为了分析不同车辆配置对调度结果的影响，本节将车辆配置情况分为3类，包括所有车辆均为K1类型（即舱位配载类型固定）、K2类型（即舱位配载类型不固定）以及混合类型（即同时存在K1和K2类型的油罐车，本节中令二者比例为1:1）。由于实际运营中，K2类车辆需要支付额外的清洗费用，其固定派车成本远高于K1类车辆，因此本节仅讨论车辆配置对运输成本以及车载率的影响，表4展示了针对算例A0-R，A1-R，A2-R，在不同车辆配置情况下各执行参数的取值。

表4 运行结果中各执行参数的取值

从表4可以看出，不同车辆配置下，同一算例对应的派车数均相等，这在一定程度上说明了求解结果的有效性和稳定性。此外，得益于K2类型车辆舱位配载类型不固定的特点，与其他类型的车辆配置相比，采用K2类型的车辆配置能够扩大搜索空间，并有效的适应当前配送需求，能够得到运输成本最小且车载率较高的配送方案。但同时，由于K2类型车辆的固定派车成本较高，因此尽管其运输成本较小，但其总成本却远高于其他类型，算例中，其运输成本占总成本的比重远低于其他车辆配置类型。

表5 两种车辆配置下的优化解及车舱配载方案

此外，分析可知，若K1类车辆的车舱配载类型接近或达到当前配送需求的最优配载方案，此时采用K1类车辆执行配送方案既能有效降低配送成本，同时也能提高平均车载率。为了验证上述结论，针对算例A0-R，分别扩大K1和K2类车辆的规模（其中K1类在增加车辆数目的同时，尽可能多样化每个舱位的装载类型），并调用本文算法进行求解，最终对比两种车辆配置下的优化解及车舱配载方案结果如表5所示。同时，为直观的反应两种配送方案的差异，图7展示了上述两种配置下的车辆行驶路径。可知，两种车辆配置情况下所得的配送路径具有相似性，并且除了由于K2类车辆的单位固定派车成本较高，导致固定派车成本差异较大以外，其他执行参数（包括执行车辆数、车型选择、车舱配载方案、运输成本以及平均车载率）均相等或小范围变化。综上所述，当K1类车辆的舱位配载方案达到或接近当前配送需求的最优配置时，能够有效的降低总成本并提高车辆利用率；对于成品油多舱配送来说，K2类车辆配置的情况，类似于油品换季时，配送中心对油罐车进行统一清罐后的情况，因此，配送中心需要提前预估下个季度每个加油站每种油品的需求情况，并以此为依据对清罐后的车辆进行配载指派；并且，在配送期间，若当前的舱位配载方案不能满足配送需求，需要及时对部分车辆进行清罐处理并调整配载方案。

进一步的分析可知，相较于K1类型和混合类型的车辆配置，尽管K2类型车辆配置能够获得更优的平均车载率，但由于满舱配载、硬时间窗、以及车型限制等约束的存在，使得优化方案不可避免的出现了舱位空载的现象。尤其是当时间窗较窄时，需要以牺牲车载率为代价满足上述配送约束。为体现硬时间窗的特点，本文算例的时间窗宽度均设置较窄，而在实际配送中，加油站补货时间窗的设置并不一定严格（均为窄时间窗），因此，平均车载率可达到更高值。为验证时间窗对车辆装载率的影响，针对算例A0-R，将所有订单的时间窗宽度扩大5倍（即尽可能保证在任意情况下，配送方案均满足时间窗需求），调用本文算法可知在K1类、K2类、混合类车辆配置情况下，配送方案的车辆使用数平均减小了21%，同时平均车载率可分别达到78.16%，94.21%，86.38%。上述分析也说明了有效的补货时间窗设定，能进一步提高车辆利用率。

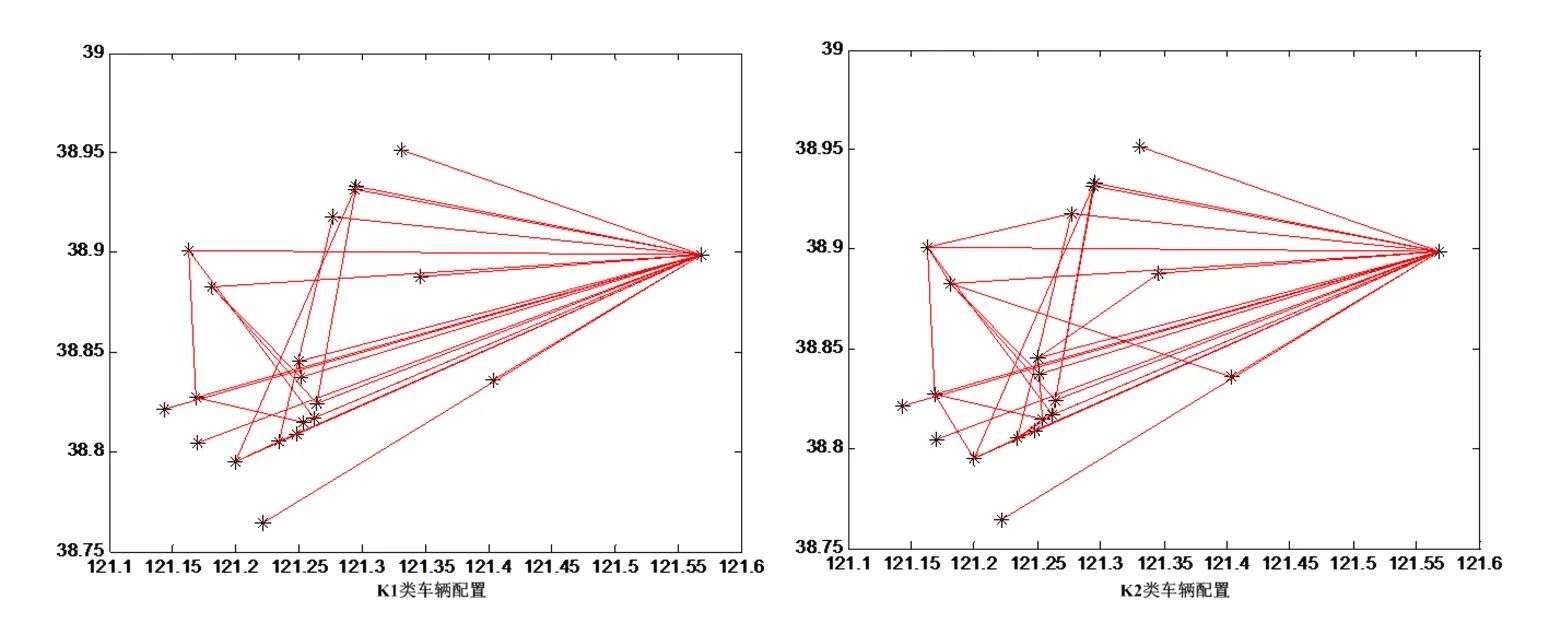
图7 两种车辆配置下的车辆行驶路

Figure 7 Driving route under two kind of truck configurations

8 结论

文中针对带补货时间的成品油二次配送问题建立了多舱位、多行程、多车型、硬时间窗的车辆路径问题模型，将原问题（MCMTVRPTW）分解为带时间窗的多舱位车辆路径问题（MCVRPTW）和有车辆数量限制的多行程指派问题（MAPLV），通过引入行程池的概念，按先行程后分组的求解策略设计了包含内外两层循环的启发式算法。其中，外循环通过最大评价因子顺序插入法及行程选择算法构造MCVRPTW问题的初始解和可行解，而内循环采用行程分配算子用于行程的指派并对部分车辆的舱位配载类型进行安排；同时，还调用多种局部搜索算子对原问题可行解进行再优化。本文结合大连市中石化加油站的分布情况，构造多组算例验证了上述模型和算法的有效性，算例结果表明：（1）本文设计的求解算法性能稳定且有效，其中，最大评价因子顺序插入法能够快速生成较优的MCVRPTW问题初始解，而后优化算子能够以牺牲部分求解时间为代价搜寻到更优秀的可行解。（2）针对同一配送区域，不同补货时间窗分布会对调度结果产生不同的影响，其中，聚集分布的时间窗会增加派车量，其车辆周转次数较低，但时间利用率最高；分布均匀的时间窗，其车辆周转次数和时间利用率均处在较高水平；此外，有效的交通管制措施，能在降低配送成本的同时，提高车辆利用率。（3）尽管派车成本较高，但由于舱位装载的灵活性，舱位配载类型不固定的车辆配置能够在降低运输成本的同时提高车载率；而当现有车舱配载类型接近或达到当前配送需求的最优配置时，总成本将得到极大降低，同时车载率也能得到有效提升。

[1] 宋洁蔚,荣冈.成品油配送中时间窗的确定及运输的安排[J]. 系统工程理论与实践,2003,(04):63-69+81.

Song J W, Rong G. Time Window Confirmation and Transportation Arrangement of Oil Distribution [J]. Systems Engineering-Theory Practice, 2003,(04):63-69+81.

[2] 熊静进.成品油配送中车辆优化调度问题的研究与应用[D].武汉大学,2005.

Xiong J J. The Research of Vehicle Routing Problem in oil distribution [D].Wuhan University, 2005.

[3] 孙丽君.成品油配送干扰管理问题决策情境的表示方法研究[A]. 中国系统工程学会.中国系统工程学会第十八届学术年会论文集——A01系统工程[C].中国系统工程学会:2014:3.

Sun L J.Representation of decision scenario for disruption management of petroleum products distribution. Systems Engineering Society of China. Proceeding of 18th Annual Conference of Systems Engineering Society of China-A01 Systems Engineering [C]. Systems Engineering Society of China: 2014: 3.

[4] 李敏,倪少权,周凌,等.基于订单邻域的成品油二次配送中带时间窗车辆路径规划问题[J].计算机集成制造系统,2015,21(8):2158-2169.

Li M, Ni S Q, Zhou L, et al. Vehicle routing problem with time windows of petroleum products distribution based on order neighborhood system[J]. Computer Integrated Manufacturing Systems, 2015, 21(8): 2158-2169.

[5] 张源凯,孙丽君,胡祥培.成品油配送多车舱车辆指派及路径优化问题研究[J].运筹与管理,2017,26(07):1-9.

Zhang Y K，Sun L J，Hu X P, Multi-compartment Vehicle Dispatching and Routing for Product Oil Distribution[J].Operations Research and Management Science,2017,26(07):1-9.

[6] 张立峰,易万里,刘晓兰.基于两阶段算法的大规模成品油二次配送优化[J].系统工程理论与实践,2016,36(11):2951-2963.

Zhang L F, Yi W L, Liu X L. Two-stage optimization algorithm for large scale secondary petroleum product delivery planning[J]. Systems Engineering-Theory Practice, 2016, (11): 2951-2963.

[7] Cornillier F, Boctor F, Laporte G, et al. A heuristic for the multi-period petrol station replenishment problem [J]. European Journal of Operational Research, 2008, 191(2): 295-305.

[8] Cornillier F, Boctor F, Renaud J. Heuristics for the multi-depot petrol station replenishment problem with time windows [J]. European Journal of Operational Research, 2012, 220(2): 361-369.

[9] Boctor F, Renaud J, Cornillier F. Trip packing in petrol stations replenishment [J]. Omega, 2011, 39(1): 86-98.

[10] Cornillier F, Laporte G, Boctor F, et al. The petrol station replenishment problem with time windows [J]. Computers & Operations Research, 2009, 36(3): 919-935.

[11] Vidović M, Popović D, Ratković B. Mixed integer and heuristics model for the inventory routing problem in fuel delivery [J]. International Journal of Production Economics, 2014, 147(147): 593-604.

[12] Popović D, Vidović M, Radivojević G. Variable neighborhood search heuristic for the inventory routing problem in fuel delivery [J]. Expert Systems with Applications, 2012, 39(18): 13390-13398.

[13] Prins C, Lacomme P, Prodhon C. Order-first split-second methods for vehicle routing problems: A review[J]. Transportation Research Part C, 2014, 40(1):179-200.

[14] Beasley J E. Route first—Cluster second methods for vehicle routing[J]. Omega, 1983, 11(4):403-408.

[15] 吕圣杰.我国成品油二次配送路径优化分析[J].中国储运,2016(2):118-120.

Lv S J.Optimization analysis of secondary petroleum product delivery in China.China Storage and Transport,2016(2):118-120.

[16] 余国印.成品油二次物流配送车辆调度问题研究[D].重庆交通大学,2016.

Yu G Y, Research on Vehicle Scheduling Problem Of the Refined Oil Secondary Logistics Distribution[D].Chongqing Jiaotong University, 2016.

[17] 程少雄.基于C-W节约算法成品油二次配送车辆路线优化研究[D].长安大学,2015.

Chen S X. The Research of Refined Oil Secondary Distribution Vehicle Route Optimization Problem Based on the C-W Saving Algorithm[D].Chang’an University.2015.

[18] 李敏,黄强,周凌,等.面向对象Petri网的成品油配送模型构建研究[J].计算机工程与应用, 2015, 51(20):55-61.

Li M, Hung Q, Zhou L. et al. Research on modeling of petroleum products distribution system based on object-oriented Petri nets[J]. CEA, 2015, 51(20): 55-61.

[19] 林宇肖.考虑油品隔离的成品油城市配送路径优化[D].大连海事大学,2015.

Lin Y X, Vecicle Routing Optimization of the Refined Oil Product Redistribution Considering the Isolation[D].Dalian Maritime University,2015.

[20] Villegas P A, Albornoz V M. Large Scale Petrol Station Replenishment Problem with Time Windows: A Real Case Study[C]// International Conference on Operations Research and Enterprise Systems. 2016:408-415.

[21] Benantar A, Ouafi R, Boukachour J. A Petrol Station Replenishment Problem: New Variant and Formulation[C]// IEEE International Conference on Logistics Operations Management. IEEE, 2014.

[22] Carotenuto P, Giordani S, Massari S, et al. A Multi-depot Periodic Vehicle Routing Model for Petrol Station Replenishment [J]. 2016.

[23] Triki C, Al-Hinai N. The Periodic Petrol Station Replenishment Problem: An Overview[C]// Biennial Conference of the Indian Society of Industrial and Applied Mathematics. 2015.

[24] Wassan N, Wassan N. The Multiple Trip Vehicle Routing Problem with Backhauls[J]. Computers & Operations Research, 2017, 78(C):454-467.

[25] Braga N, Alves C, Macedo R. Exact Solution of the Multi-trip Inventory Routing Problem using a Pseudo-polynomial Model[C]// International Conference on Operations Research and Enterprise Systems. 2017:250-257.

[26] Grangier P, Gendreau M, Lehuédé F, et al. An adaptive large neighborhood search for the two-echelon multiple-trip vehicle routing problem with satellite synchronization[J]. European Journal of Operational Research, 2016, 254(1):80-91.

[27] Coelho V N, Grasas A, Ramalhinho H, et al. An ILS-based algorithm to solve a large-scale real heterogeneous fleet VRP with multi-trips and docking constraints[J]. European Journal of Operational Research, 2016, 250(2):367-376.

[28] 宋强. 多行程车辆路径问题中变邻域搜索算法的应用[J]. 数学的实践与认识, 2017(19).

Song Q. The Application of Variable Neighborhood Search Algorithm for MTVRP.Journal of Mathematics in Practice and Theory, 2017(19).

[29] 梁文博. 多车程带时间窗车辆路径问题的模型和算法[D]. 大连理工大学, 2011.

Liang W B. Model and Algorithm of the Vehicle Routing Problem with Multiple Trips and Time Windows[D].Dalian University of Technology,2011.

[30] 许争争, 唐加福. 基于协作的三阶段启发式算法求解多行程车辆行程问题[J]. 南开大学学报(自然科学版), 2015(5):51-59.

Xu Z Z, Tang J F. Three-stage Algorithm to Multi-trip Vehicle Routing Problem Based on Coordination[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis(Natural Science Edition) 2015(5):51-59.

Optimization of routes for multi-compartment, multi-trip refined oil distribution with replenishment time

WANG Xuping1,2, ZHAN Hongxin1, SUN Zilai1, LI Fangfang3

(1. Institute of Systems Engineering, Dalian University of Technology, Dalian 116023, China; 2. School of Business, Dalian University of Technology, Panjin 124221, China;3. School of Management, Yangtze Normal University, Chongqing 408100, China)

Oil refining logistics integrate the functions of transportation, warehousing, distribution, information processing, and so on. They are embedded throughout the entire petrochemical industry chain and connect refineries, oil depots, and gas stations to form the complete sales network. At present, China's refined oil consumption ranks third in the world, and its refined oil industry has become important to national economic development. Domestic refined oil distribution mainly refers to the process of distributing oil products from oil depots to gas stations and consumers in society. In recent years, domestic petroleum companies have gradually introduced active oil distribution strategies to affiliated gas stations, and product storage and distribution are being actively managed, a change from the traditional passive oil model. Using advanced logistics network technology, distribution centers can monitor and predict inventory and sales of various oil products in gas stations in real time, then generate distribution orders to these stations. Therefore, achieving unified management of refined oil distribution and scheduling of transportation resources, reducing transportation costs, and improving distribution efficiency have become core issues of refined oil distribution management.

Multi-compartment Vehicle Routing Problem (MCVRP) is widely used in all aspects of social production including livestock transportation, chemical recycling, and cold chain distribution. However, unlike other applications, multi-cabin distribution of refined oil products has the following characteristics:

(1) Unless the tanker has been cleaned, the oil loading type of each compartment is fixed, that is, different types of oil are strictly prohibited to be mixed.

(2) The refined oil is a dangerously flammable and explosive product. Under the condition of non-full load, the friction between the liquid and the tank wall is likely to cause a vehicle accident, and the sloshing liquid is not conducive to the stable running of the vehicle, so the oil product distribution needs to meet the full tank load constraint.

(3) Since each oil product of the gas station has an independent storage tank, monitoring equipment and replenishment time window, the vehicle must make multiple deliveries to the same gas station to satisfy the different oil replenishment time windows. In addition, due to the requirements of full tank load and multi-type at the gas station, the single distribution of a tank truck is small, and the same tank truck needs to perform multiple distribution tasks. The average vehicle in a single cycle turns over twice, and the vehicle utilization rate is low.

In conclusion, the distribution of refined oil products needs to comprehensively consider a series of decisions, such as cabin load type assignment, multi-trip construction, multi-trip distribution, etc., and the difficulty of solving is much larger than the general vehicle routing problem. At present, domestic and foreign scholars mainly study the multi-cabin distribution problem of refined oil products from the perspective of multi-type, multi-cycle, inventory-path joint distribution, etc., and few consider the impact of practical factors such as multi-trip, multiple replenishment time windows, and multi-compartment load type. Based on the above background, this paper takes multi-trip with replenishment time window for secondary distribution route planning of refined oil products as the research object, and builds the vehicle path problem model for hard time windows, multi-compartment, multi-trip, and multi-vehicle with the combined minimum of transportation and dispatching costs.

In order to solve this problem, this paper introduces the concept of Adaptive Memory of Routes (AMR) and designs a heuristic algorithm with two layers of iterative algorithm. The algorithm divides the original problem into a Multi-compartment Vehicle Routing Problem with Time Windows (MCVRPTW) and a multi-trip distribution problem with limited vehicles (Multi-trip Assigning Problem with Limited Vehicles, MAPLV), based on the solution strategy of route-first grouping-second, wherein MCVRPTW is used for the construction of feasible trips - ignoring multi-trip in the original problem and limited vehicle constraints - to minimize the total transportation time of the vehicles, and MAPLV is used to assign limited vehicles and designate the load type of each compartment, based on the above-mentioned itinerary. Meanwhile, heuristic methods such as the sequential insertion algorithm, large neighborhood operator, trip assignment operator, and re-optimization operator are designed to solve the above two kinds of problems independently, and the original problem is continuously searched through the interactive iteration of the above two problems to reach the optimal feasible solution.

In this paper, the effectiveness of the above models and algorithms is verified by multiple simulation examples, and the following patterns are revealed through data experiments: (1) When the refueling time window of the gas station is evenly distributed, the vehicle turnover and time utilization rate are relatively high. When the distribution is concentrated, the vehicle turnover is lower and the number of dispatched vehicles is higher; the effective traffic control time setting can not only reduce the distribution cost, but also improve the vehicle utilization rate. (2) Compared with the fixed vehicle load type configuration, the non-fixed vehicle configuration is superior in terms of transportation cost and loading rate; however, when the existing compartment load type is close to or meets the current distribution requirements in an optimal configuration, a fixed load type configuration has significant advantages in terms of total cost.

Refined oil distribution; Replenishment time windows; Multi-trip; Multi-compartment; Route optimization

2017-12-10

2018-06-04

National Natural Science Foundation of China (71471025, 71531002)

TP301.6

A

1004-6062(2020)04-0182-014

10.13587/j.cnki.jieem.2020.04.020

2017-12-10

2018-06-04

国家自然科学基金资助项目（71471025、71531002）

王旭坪（1962—），男，辽宁锦州人；大连理工大学系统工程研究所教授，博士，博士生导师；研究方向：电子商务与物流管理、突发事件应急管理。

中文编辑：杜 健；英文编辑：Boping Yan