拍卖行中介下的供应链协调机制设计

秦开大，耿心宇，代建生

拍卖行中介下的供应链协调机制设计

秦开大，耿心宇，代建生

（昆明理工大学 管理与经济学院，云南 昆明 650093）

从供应链中介理论和拍卖理论相结合的角度，将拍卖机制应用于商品分销环节，考察了多零售商参与竞争下的制造商和交易中介拍卖行的协调问题。文章首先分析了零售商的均衡竞价策略，在此基础上提出了拍卖收益共享契约并证明了以下结论：存在最优的拍卖行保留价和拍卖收益分成比例能够诱导制造商的商品供应量和拍卖行的最优商品拍卖量保持一致，且能确保制造商和拍卖行整体实现利润的最大化，从而完成渠道协调。在文章的最后以一个数值算例说明了上述协调契约的可实施性和有效性，并给出了一些系统敏感度分析的结果。

供应链协调；交易中介；拍卖行；拍卖收益共享契约

0 引言

不同于传统意义上的“报童模型”，供应链中介理论（The Theory of Supply Chain Intermediation）在制造商和零售商之间引入第三方经济行为主体来协调和仲裁各供应链参与成员之间的交易行为，其常以“市场组织者”或“交易代理人”的身份出现在各种供应链网络中。有许多原因会促使制造商和零售商去选择一个第三方中介来辅助完成交易，在这里简单列举如下：其一，供应链中介往往掌握着丰富的商品供给和需求信息，能够在降低供需匹配成本，减少无效率交易，分担交易风险，降低交易成本等方面发挥出举足轻重的作用[1]。其二，在全球贸易的环境下一些制造商的商品会远销海外，对当地市场的不熟悉会给商品的销售带来种种障碍。比如，终端消费者往往要求制造商能够为其购买的商品提供一定时间的维护和维修服务，离开了本地企业的参与这样的售后服务很难进行。当制造商预计在某地直接进行商品销售的成本很高或是风险很大时，跟一个当地的中介开展合作就是一个比较合理的选择了[2]。数据显示，60%的美国制造商和70%的欧洲制造商都是借由中介将自己的商品推向海外市场的[3]。其三，由于信息不对称的存在，制造商和零售商之间的相互信任很难达成，主要表现在零售商对制造商商品质量的不信任以及制造商对零售商再销售商品内容的不信任（商品掺假、商品改装）等方面，而这又会直接影响到整个供应链的运作效率和运营成本。通过引入第三方中介来监督和规范供应链各参与成员的交易行为，承担起第三方信任机构的角色，可以有效改善供应链的运作效率，对于降低供需双方的运营成本也将大有裨益。简单来说，制造商和零售商会选择一个第三方中介来协助完成交易通常是因为这个第三方中介在商品推广、销售和技术支持等方面拥有更加专业的知识和经验，Sarker, Butler和Steinfeld指出供应链中介可以提供诸多专业服务（如商品估价、商品匹配、商品分销、风险评估、信息传播等）来改善制造商和零售商的运营绩效[4]。

对供应链中介理论的研究起源于一些经济学类文献，基于Myerson和Satterthwaite所提出的谈判理论（Bargaining Theory）[5]，Wu系统性地研究了供应链中介为什么会存在，其运作的方式以及对供应链整体效率的影响等问题[6]。Belavina和Girotra在同级供应链各参与成员间不存在直接竞争的假定条件下，比较了有中介参与和无中介参与情形下的供应链运作效率的差异。他们发现在多阶段的采购环境下，有中介参与的供应链运作效率要高于无中介参与的供应链，这是因为供应链中介手中汇聚了多个零售商的需求信息，能够对每个制造商作出一个长期的采购承诺[7]。Hingley, Lindgreen和Grant认为在竞争激烈、环境复杂的零售百货业采购供应链中引入一个第四方物流公司（4PL）作为供应链中介以促进和协调制造商和零售商之间的合作关系对于增强供应链整体的竞争实力是至关重要的[8]。Yang和Babich探讨了在由两个制造商和一个零售商组成的供应链中零售商雇佣供应链中介来辅助交易是否利大于弊的问题。他们认为由于供应链中介的参与而带来的与制造商之间的隐性共谋可在某些情形下（如在其中的一个制造商的可靠性较高，而另一个较低的情形下）降低零售商的信息收集成本[9]。Adida, Bakshi和Demiguel则考察了在什么样的市场环境下中介参与到由零售商主导下的供应链中能够有利可图，他们发现在市场供给量不是很大的情形下供应链中介反倒能够获得较多的利润[10]。Qu，Raff和Schmitt从库存管理的角度考察了供应链中介的作用，他们发现在市场需求变动性很大的情形下将商品库存分配至中介处可有效提高供应链整体绩效[11]。Wu依照中介在供应链中所发挥的主要职能的不同将供应链中介分为两大类：一类是交易中介，他们借由持有库存、汇聚需求等服务来提高买卖双方的交易效率；另一类是信息中介，他们借由建立起第三方信任机构等方式来降低制造商和零售商之间信息不对称的风险[6]。考察以上文献，其中的中介多是作为信息中介而发挥作用，而鲜有文献考虑交易中介在供应链中联系买卖双方的运作方式和均衡行为（Qu，Raff和Schmitt的研究是有关交易中介的不多见的一例[11]），本文将在这一方面对现有文献作出补充。本文将考虑有拍卖行参与的供应链的协调机制的设计，其中的拍卖行作为交易中介借助拍卖的形式将制造商生产的商品分销给各个零售商，并从中获取拍卖收益分成，而未售出商品的残值将在拍卖行处得以实现。

拍卖作为一种流行的交易机制，其主要的特点是具有价格发现功能，能够有效降低搜寻与谈判的成本，使交易结果更趋公平与公正，争议少，效率高。由于其具有简单而稳健的需求分配机能，拍卖不仅在理论上得到了很好的研究[12-14]，也在实践中被广泛应用于诸如农产品、艺术品、珠宝、无形资产以及各种使用权的销售中[15]。将拍卖这样一种相对成熟的交易机制引入到供应链的管理中来，无疑将有效解决商品分配的难题，提高供需匹配的效率，进而改善整个供应链运营的绩效。近几年，已有不少学者尝试将拍卖与供应链结合起来研究，Jin和Wu在采购环境下探讨了如何使用二部制契约拍卖（Two-Part Contract Auction）来协调供应链的问题[16]。马俊和张杰等则拓展了Jin和Wu的研究模型，得到了更为一般性的结论[17-19]。Chen和Vulcano考察了在供应链中仅存在一个制造商和两个零售商并允许二次销售的情形下信息公开对于零售商在第一以及第二价格拍卖机制下的均衡收益的影响[20]。Tunca和Wu分析比较了拍卖机制在多种不同投标环境下的应用，并提出了一种全新的两阶段采购方案：零售商在第一阶段运用拍卖机制粗选出最富有竞争力的若干制造商，而把向每个制造商采购的商品数量和所需支付的采购价格的决策放在第二阶段[21]。周学广, 张坚和梅强等对在多个制造商和一个零售商之间进行的单轮多属性逆向拍卖建立起了一个非合作博弈模型，结果表明零售商并不会根据最低的投标价格而是根据投标质量和交货期的最优组合来选择制造商[22]。Rao, Zhao和Ma设计了一种满足激励相容（Incentive Compatible）和个体理性（Individual Rationality）条件的多属性拍卖机制用来帮助零售商筛选优质的制造商[23]。Wang设计了一种或有支付拍卖机制（CPAM）用于多属性采购过程[24]。陈树广和刘小冬证明了在市场中存在多个制造商、一个零售商和一个第三方回收商的情形下，满足一定条件的目录拍卖-双重奖惩契约机制能够协调闭环供应链[25]。纵观以上文献可以发现几乎所有的文献都把研究的重点放在商品的采购环节，对于拍卖机制在商品分销环节的应用鲜有文献涉及。本文将填补上这一研究空缺，将拍卖机制应用于商品分销环节，交易中介拍卖行将采用第一价格密封拍卖把制造商生产的商品分销给各个零售商。

如前文所述，在供应链中介理论研究和利用拍卖机制来改善供应链运营绩效等两方面都已有学者作出了一些卓越的研究成果。然而，将这两方面加以结合，即如何运用拍卖机制来改善有中介参与的供应链的运营绩效的问题还几乎没有学者研究探讨过。据我们所知，唯一一篇有参考价值的文献是Lorentziadis所做的研究。在他的文章中，制造商采用低价密封拍卖机制来选择最优的供应链中介。Lorentziadis考察了各个供应链中介的均衡竞价行为以及制造商的均衡收益，并探讨了信息不对称对供应链运营绩效的影响[26]。本文的研究与Lorentziadis的又有所不同，制造商将自己的商品委托交易中介拍卖行代为销售，而拍卖行采用第一价格密封拍卖将商品分销给相应的零售商，并与制造商共享拍卖收益。本文以制造商移交给拍卖行的商品供应量为调整对象，提出了拍卖收益共享契约并证明了以下结论：存在最优的拍卖保留价和拍卖收益分成比例能够诱导制造商的商品供应量和拍卖行的最优商品拍卖量保持一致，且能确保制造商和拍卖行整体实现利润的最大化，从而完成渠道协调。

1 问题描述

2 零售商的竞价策略

等价地有

3 最优拍卖收益共享契约

下面考虑制造商与拍卖行之间的拍卖收益共享契约的设计问题。为了行文方便，后文用“供应链子系统”一词特指原供应链的商品供给环节，即制造商和拍卖行组建的供应链系统。作为比较的标准，先讨论供应链子系统在集中决策模式下的最优决策问题，再考察分散决策模式下的决策问题，并通过比较的方式确定供应链子系统的最优拍卖收益共享契约。

3.1 供应链子系统集中决策

由于供应链经营的商品具有报童属性，供应链子系统面临以下决策问题：在考虑到零售商的策略反映基础上，确定商品供给量用于拍卖，以最大化供应链子系统的利润。

首先注意到单件商品经过拍卖途径可实现的期望收益为

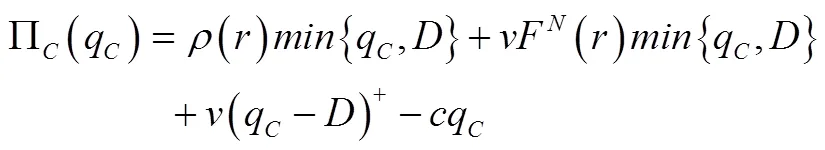
其期望利润函数为

3.2 供应链子系统分散决策

期望利润函数为

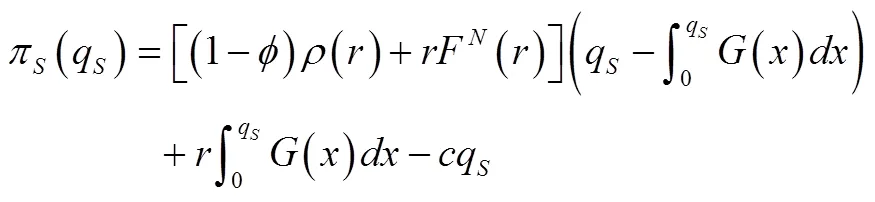
证明：首先注意到

3.3 供应链子系统的最优拍卖收益共享契约

下面对定理2的后一部分结论进行证明。

定理2不仅证明了供应链子系统最优拍卖收益共享契约的存在性，还刻画了最优拍卖收益共享契约参数之间的函数关系。

4 数值算例

本节将结合一个具体的数值算例，详细阐述如何运用以上的结论来确定最优的拍卖收益共享契约参数，在表明该协调契约的可实施性的同时还将验证其有效性。在阐明了最优拍卖收益共享契约的计算方法后，本文还将调整上述算例中的输入变量值，通过重新计算最优的契约参数和相应的系统绩效来分析该供应链子系统对于环境变化的敏感度，并据此给出一些实验性的管理启示。

4.1 最优拍卖收益共享契约参数的确定

图1 最优拍卖收益共享契约参数的确定

Figure 1 Deriving the optimal parameters for the auction revenue sharing contract

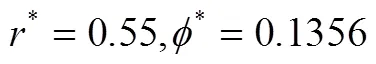
4.2 供应链子系统的敏感度分析

图2 拍卖收益共享契约参数对供应链利润分布的影响

Figure 2 The effect of the auction revenue sharing contract parameters on the supply chain profit distribution

表1 参与竞拍的零售商数量对供应链子系统运营绩效的影响

表2 零售商对单位商品的估价分布对供应链子系统运营绩效的影响

表3 市场对商品需求量的均值对供应链子系统运营绩效的影响

表4 市场对商品需求量的方差对供应链子系统运营绩效的影响

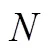
5 结束语

本文从供应链中介理论和拍卖理论相结合的角度研究了拍卖行中介下的供应链协调机制的设计问题。文章将拍卖机制应用于商品分销环节，提出并证实了以拍卖行保留价和拍卖收益分成比例为契约参数的拍卖收益共享契约能够在个体理性的约束条件下诱导制造商的商品供应量与拍卖行的最优商品拍卖量保持一致，并且使得制造商和拍卖行的整体利润实现最大化，从而完成渠道协调。在文章的最后给出了一个数值算例，在说明最优拍卖收益共享契约的可实施性和有效性的同时，还对模型的部分参数作出了敏感度分析。

本文虽在一定程度上弥补了现有文献对交易中介和拍卖机制在商品分销环节研究的不足，但是文中所建立的模型尚需进一步地加以拓展以适用于更为广泛的情形。其拓展的方向可从以下两方面入手：其一，本文仅讨论了在市场中只存在一个制造商的情形下的渠道协调问题，对于有多个制造商参与市场竞争的情形还需要进一步的研究和讨论，这可能需要构建一个以拍卖行为交易中介的双边拍卖模型。其二，本文假设制造商的生产成本信息是公开的，而实际上制造商为了获得较大的收益分成比例可能会谎报自己的生产成本信息。在这种信息不对称的情形下，需要重新审视制造商和拍卖行各自的均衡策略，并调整相应的拍卖收益共享契约来优化整个供应链的运作效率。

[1] Spulber D F. Market microstructure[M]. Cambridge: Cambridge University Press, 1999.

[2] Arnold D. Seven rules of international distribution[J]. Harvard Business Review, 2000, 78(6): 131-137.

[3] Jobber D. Principles and practice of marketing[M]. New York: McGraw Hill, 2010.

[4] Sarker M, Butler B, Steinfeld C. Intermediaries and cybermediairies: a continuing role for mediating players in the electronic marketplace[J]. Journal of Computer-Mediated Communication, 1995, 1(3).

[5] Myerson R B, Satterthwaite MA. Efficient Mechanisms for Bilateral Trading[J]. Journal Of Economic Theory, 1983, 29: 265-281.

[6] Wu S D. Supply chain intermediation: a bargaining theoretic framework[A]. In: Simchi-Levi D, Wu SD, Shen Z-J. Handbook of Quantitative Supply Chain Analysis[M]. Boston: Springer US, 2004: 67-115.

[7] Belavina E, Girotra K. The Relational Advantages of Intermediation[J]. Management Science, 2012, 58(9): 1614-1631.

[8] Hingley M, Lindgreen A, Grant DB. Intermediaries in power-laden retail supply chains: An opportunity to improve buyer-supplier relationships and collaboration[J]. Industrial Marketing Management, 2015, 50: 78-84.

[9] Yang Z B, Babich V. Does a Procurement Service Provider Generate Value for the Buyer Through Information About Supply Risks?[J]. Management Science, 2015, 61(5): 979-998.

[10] Adida E, Bakshi N, Demiguel V. Supplier Capacity and Intermediary Profits: Can Less Be More?[J]. Production and Operations Management, 2015, 25(4): 630-646.

[11] Qu Z, Raff H, Schmitt N. A Theory of Intermediation in Supply Chains Based on Inventory Control[R]. Dresden: Technische Universität Dresden, CEPIE Working Papers, 2016.

[12] Vickrey W. Counterspeculation, Auctions, and Competitive Sealed Tenders[J]. Journal of Finance, 1961, 16(1): 8-37.

[13] Milgrom P R, Weber R J. A Theory of Auction and Competitive Bidding[J]. Econometrica, 1982, 50(5): 1089-1122.

[14] Greenleaf E A, Rao A G, Sinha A R. Guarantees in Auctions: The Auction House as Negotiator and Managerial Decision Maker[J]. Management Science, 1993, 39(9): 1130-1145.

[15] Milgrom P. Putting Auction Theory to Work[M]. Cambridge: Cambridge University Press, 2003.

[16] Jin M, Wu S D. Coordinating Supplier Competition via Auctions[R]. Pennsylvania: Lehigh University, 2004: 123-129.

[17] 马俊, 张杰, 汪寿阳. 应用拍卖机制协调供应链[J]. 管理科学学报, 2009, 12(5): 1-9.

Ma J, Zhang J, Wang S-Y. Coordinate supply chain via auction mechanisms[J]. Journal of Management Sciences in China, 2009, 12(5): 1-9.

[18] 马俊, 张杰, 张芳. 完全信息采购环境下应用拍卖机制协调供应链[J]. 管理学报, 2009, 6(10): 1291-1295.

Ma J, Zhang J, Zhang F. Coordinate Supply Chain Via Auction Mechanisms under Procurement Environment with Complete Information[J]. Chinese Journal of Management, 2009, 6(10): 1291- 1295.

[19] 马俊, 张杰. 不完全信息采购环境下的供应链协调问题：拍卖机制的应用[J]. 中国管理科学, 2009, 17(6): 70-77.

Ma J, Zhang J. Coordinate Supply Chain via Auction Mechanisms under Procurement with Incomplete Information[J]. Chinese Journal of Management Science, 2009, 17(6): 70-77.

[20] Chen Y-J, Vulcano G. Effects of Information Disclosure under First- and Second-Price Auctions in a Supply Chain Setting[J]. Manufacturing & Service Operations Management, 2009, 11(2): 299-316.

[21] Tunca T I, Wu Q. Multiple sourcing and procurement process selection with bidding events[J]. Management Science, 2009, 55(5): 763-780.

[22] 周学广, 张坚, 梅强, 等. 基于多属性逆向拍卖的博弈分析[J]. 管理工程学报, 2011, 25(2): 200-205.

Zhou X G, Zhang J, Mei Q,. A Game Analysis on Multi-attribute Reverse Auctions[J]. Journal of Industrial Engineering/Engineering Management, 2011, 25(2): 200-205.

[23] Rao C, Zhao Y, Ma S. Procurement decision making mechanism of divisible goods based on multi-attribute auction[J]. Electronic Commerce Research and Applications, 2012, 11(4): 397-406.

[24] Wang H. Contingent payment auction mechanism in multidimensional procurement auctions[J]. European Journal of Operational Research, 2013, 224(2): 404-413.

[25] 陈树广, 刘小冬. 采购拍卖下混合回收渠道的闭环供应链奖惩契约协调研究[J]. 统计与信息论坛, 2014, 29(5): 72-77.

Chen S G, Liu X D. Research on Coordination of Closed-loop Supply Chain with Hybrid Recycling Channels Via Procurement Auction and Dual Reward and Punishment Contract[J]. Statistics & Information Forum, 2014, 29(5): 72-77.

[26] Lorentziadis P L. Pricing in a supply chain for auction bidding under information asymmetry[J]. European Journal of Operational Research, 2014, 237: 871-886.

[27] Greenleaf E A, Ma J, Qiu W,. Note on “Guarantees in Auctions: The Auction House as Negotiator and Managerial Decision Maker”[J]. Management Science, 2002, 48(12): 1640-1644.

[28] 刘树林. 担保拍卖理论研究[J]. 数量经济技术经济研究, 2004, (12): 44-53.

Liu S L. A Theoretical Study on Guaranteed Auctions[J]. The Journal of Quantitative & Technical Economics, 2004, (12): 44-53.

[29] Riley J G, Samuelson W F. Optimal Auctions[J]. American Economic Review, 1981, 71(3): 381-392.

[30] Myerson R. Optimal Auction Design[J]. Mathematics of Operations Research, 1981, 6(1): 58-73.

Coordination mechanism design for a supply chain intermediated by an auction house

QIN Kaida, GENG Xinyu, DAI Jiansheng

(Faculty of Management and Economics, Kunming University of Science and Technology, Kunming 650093, China)

Considering the important role of supply chain intermediaries in improving transaction efficiency, reducing transaction risks, and improving the overall operating performance of the supply chain, many manufacturers and retailers tend to choose a third-party intermediary to complete their transaction. This article discusses a supply chain coordination model in which third-party intermediaries are involved - that is, manufacturers distribute goods to retailers through auction houses, and auction houses obtain a share of auction revenue from them.

Compared to the existing literature, the research in this paper has the following three distinguishing characteristics: First, the auction house is used as a transaction intermediary instead of an information intermediary, to improve the transaction efficiency of buyers and sellers; second, the auction mechanism applies to the distribution of goods rather than the procurement of commodities; third, combining the theory of supply chain intermediation and auction, this paper evaluates how to use the auction mechanism to improve the performance of the supply chain with the participation of intermediaries.

Consider a supply chain consisting of a manufacturer, N retailers, and a transaction intermediary - that is, the auction house in the supply chain. Commodities are distributed according to the following steps: First, before the auction begins, the manufacturer and the auction house sign a revenue sharing contract that includes the parameters of the reserve price and the revenue share ratio; then, the manufacturer delivers a certain number of commodities to the auction house, and the auction house determines the number of commodities to put up for auction; finally, the auction house auctions the commodities in the format of a first-price sealed-bid auction with a reserve price for the retailers, and shares the revenue with the manufacturer according to the ratio specified in the revenue sharing contract. In order to determine the optimal contract parameters to coordinate the supply chain, we take the following three steps.

First, under the assumption that all retailers follow a symmetrical, incremental, and differentiable equilibrium bidding strategy, the retailers’ optimal bidding strategy is solved. In the first-price sealed-bid auction format with a reserve price, the retailers’ equilibrium bidding strategy is as follows: if the commodity’s true valuation is lower than the reserve price, its bid quote will not be higher than the reserve price and will not affect the auction result; otherwise, if the commodity’s valuation is higher than the reserve price, its bid quote is a strictly increasing function of both its valuation and reserve price, and will not be higher than its valuation.

Second, the manufacturers and auction houses are regarded as a "subsystem of the supply chain", and the optimal strategic responses of their participating members in the case of centralized and decentralized decisions are discussed. In the case of centralized decision-making, manufacturers and auction houses have an incentive to engage in the business activities of the commodity only when the expected realizable benefits of the commodity are greater than its production costs; in the case of decentralized decision-making, regardless of the quantity of the commodity supplied by the manufacturer, the auction house will auction all the supplied goods, and the manufacturer’s willingness to supply a certain quantity of goods to the auction house depends on the size of its portion of the revenue share ratio.

Finally, by comparing and analyzing the optimal response functions of manufacturers and auction houses in the case of centralized and decentralized decisions, this paper not only proves the existence of optimal parameters for auction revenue sharing contracts, but also provides an approach to derive them. The quantity of goods supplied by the manufacturer, influenced by this optimal revenue sharing contract, can facilitate channel coordination throughout the supply chain. At the end of this paper, a numerical example is provided to illustrate the feasibility and effectiveness of the optimal contract. Simultaneously, a sensitivity analysis is also performed for exogenous variables in the model.

Supply chain coordination; Transaction intermediary; Auction house; Auction revenue sharing contract

2018-01-04

2018-06-15

Supported by the Natural Science Foundation of China (71362025, 71162019)

F724.59

A

1004-6062(2020)04-0135-009

10.13587/j.cnki.jieem.2020.04.015

2018-01-04

2018-06-15

国家自然科学基金资助项目（71362025、71162019）

秦开大（1971—），男，湖北潜江人；昆明理工大学管理与经济学院院长、教授；主要从事运营管理、拍卖理论的研究。

中文编辑：杜 健；英文编辑：Boping Yan