如何正确运用t检验——线性回归模型中参数与0比较t检验及SAS实现

2020-09-09黄慧杰刘媛媛李长平胡良平

四川精神卫生 2020年4期

黄慧杰，刘媛媛 *，李长平，2，胡良平

（1.天津医科大学公共卫生学院，天津 300070；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3.军事科学院研究生院，北京 100850*通信作者：刘媛媛，E-mail：ivyuan10@126.com）

回归分析是医学研究中常用的分析方法，其中，线性回归分析是最常用、最简单的一种。线性回归分析是通过建立因变量随单个或多个自变量按线性关系变化的方程式并检验整个方程式和参数是否具有统计学意义。严格地说，线性回归分析的自变量应该是定量的，但在实际应用中，自变量的范围被拓展了，包括二分类变量、进行哑变量变换后的多分类变量及多值有序变量，而因变量必须是定量变量。含单个因变量和单个自变量的线性回归模型被称为简单线性回归模型；含单个因变量和多个自变量的线性回归模型被称为多重线性回归模型［1］。在线性回归分析中，需要对整个回归模型和模型中的各参数进行假设检验，对回归模型整体检验采用的是方差分析；对参数检验采用的是t检验。本文着重探讨t检验对简单线性回归模型和多重线性回归模型的参数与0之间差异进行假设检验的原理与应用。

1 基本概念

1.1 参数和统计量

参数是用来描述总体特征的概括性数字度量，是研究者想要了解的总体的某些特征值。依据经典统计学的观点，由于总体数据通常是未知的，所以参数是一个未知的常数［2］。设x1，x2，…，xn为取自某总体的样本，若样本函数T（x1，x2，…，xn）中不含有任何未知参数，则称T为样本统计量［3］。由于样本是已经抽取出来的，所以样本统计量是已知的，抽样的目的就是用样本统计量去估计总体参数。也就是说，一旦选定了一个参数，就必然有一个统计量与之对应。

常用一元一重线性回归模型为：

上式中，β0是直线在y轴上的截距，β1是直线的斜率，而ε是y轴方向上的随机误差。一般假定：ε服从均值为0、方差为σ2的正态分布。由于β0和β1是未知参数，一般采用最小二乘法对β0和β1进行估计。β0的估计值为的估计值为：

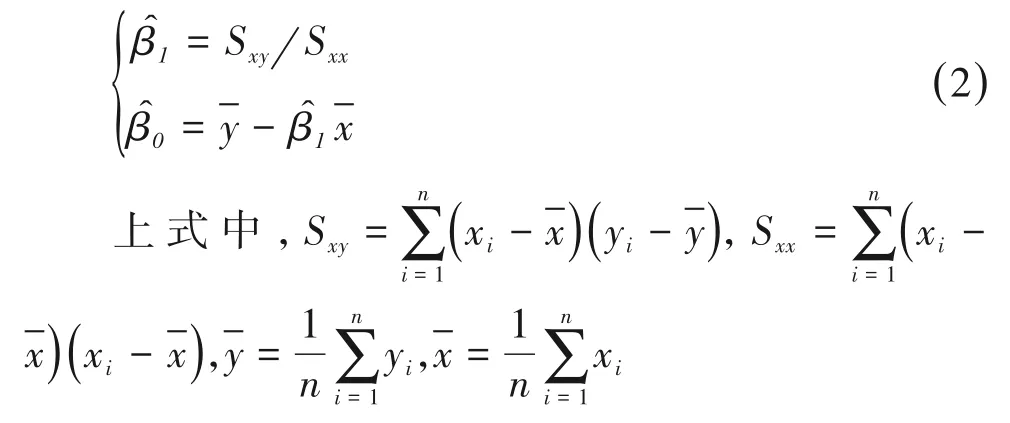
β0和β1都叫做参数，而就是两个参数的估计值，都叫做样本统计量。在多重线性回归分析中也具有类似的参数和样本统计量，只是被称为“斜率”的参数和样本统计量的数目≥2。

具有k个自变量的多重线性回归模型可表示如下：

上式中，β0，β1，β2，…，βk均是多重线性回归模型的参数，ε是y轴方向上的随机误差。一般假定：ε服从均值为0、方差为σ2的正态分布。同样也采用最小二乘法来估计多重线性回归模型中的各个参数。对于n组数据，可得到以下由多重线性回归模型中参数的估计值组成的向量：

上式中，XT是X（被称为设计矩阵）的转置矩阵，都是列向量。

1.2 简单线性回归模型中截距与0之间差异的t检验

在简单线性回归分析中对截距进行假设检验的原假设和备择假设分别为：

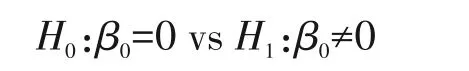
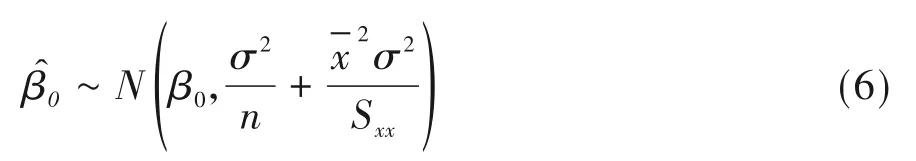
通过转换为标准正态分布可得：

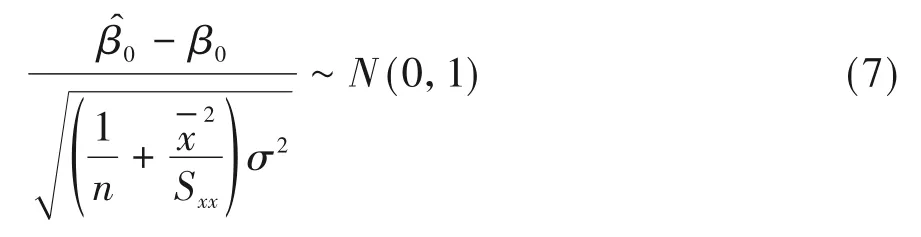
根据以上公式可得如下检验统计量：

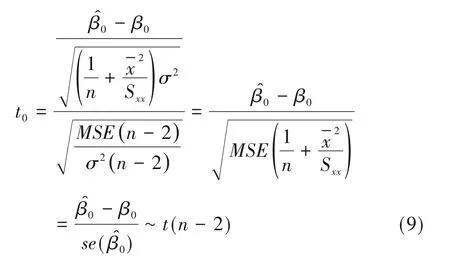
当原假设为真，即β0=0时，服从自由度为n-2的t分布。当|t0|＞t0.025(n-2)或t0对应的P值小于0.05时，可认为β0与0之间差异有统计学意义。

1.3 简单线性回归模型中斜率与0之间差异的t检验

在简单线性回归分析中对斜率进行假设检验的原假设和备择假设分别为：

转换为标准正态分布得：

由此可得检验统计量：

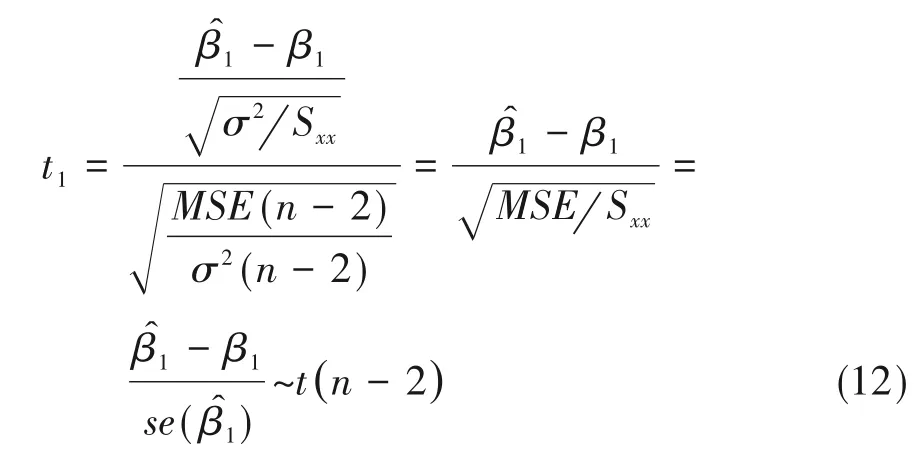
当原假设为真时，即β1=0 时，有服从自由度为n-2的t分布。当|t1|＞t0.025(n-2)或者t1对应的P值小于0.05时，可认为β1与0之间的差异有统计学意义。

1.4 多重线性回归模型中参数与0之间差异的t检验

在多重线性回归模型中对参数βj（0≤j≤k）进行假设检验的原假设和备择假设分别为：

多重线性回归模型中的参数βj的检验统计量tj服从自由度为n-k-1的t分布［4］：

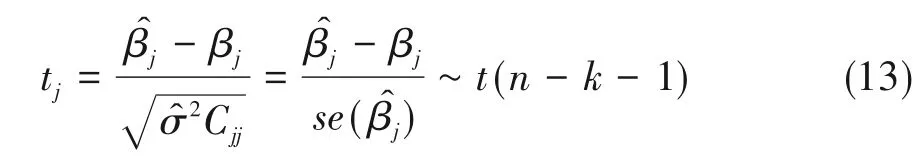
上式中，Cjj是k阶矩阵（XTX）-1中第j行第j列位置上的元素。

当原假设为真时，即βj=0时，有服从自由度为n-k-1的t分布。当|tj|＞t0.025(n-k-1)或者tj对应的P值小于0.05时，可认为βj与0之间的差异有统计学意义。

2 简单线性回归模型中参数与0之间差异t检验的实例

2.1 简单线性回归分析的数据结构

【例1】研究20名儿童血红蛋白（y）与血铁（x）之间的关系［5］。数据见表1。

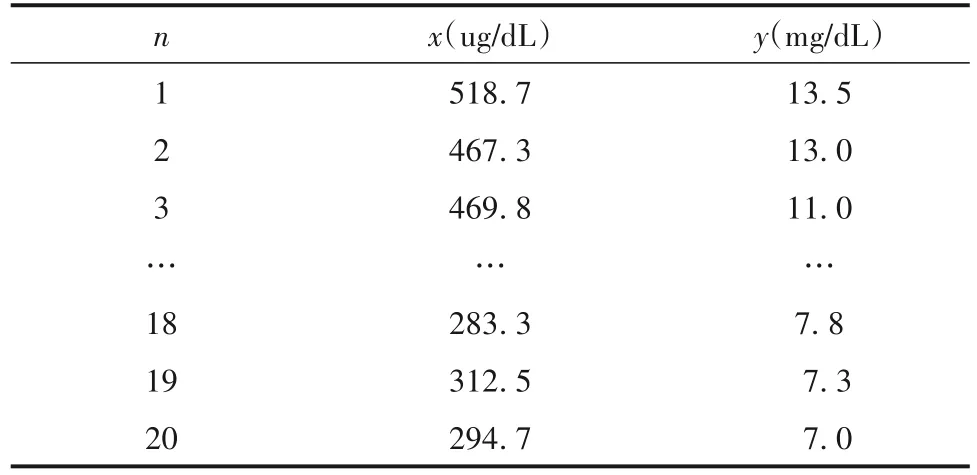
表1 20名儿童血红蛋白（y）与血铁（x）的测定资料

通过t检验来判断简单线性回归模型中的截距（β0）和斜率（β1）与0之间差异是否有统计学意义，若斜率与0之间差异有统计学意义，则说明血红蛋白与血铁之间存在着线性依赖关系，即血红蛋白会随着血铁的变化呈线性变化趋势。

2.2 构建与求解简单线性回归模型的SAS程序

根据例1中数据进行简单线性回归分析，并对回归方程的截距和斜率进行t检验。

SAS程序如下：

【程序说明】以上SAS程序由1个数据步和3个过程步构成。数据步建立例1中的数据集test1，输入20例儿童的血铁（x）和血红蛋白（y）数据。第一个过程步调用REG过程，建立简单线性回归方程，并对总体和参数进行检验。第二个过程步也调用REG过程，但通过noint语句删除了方程的截距项，是对第一个过程步的调整。第三个过程步调用SGPLOT过程，通过scatter语句绘制散点图，通过reg语句绘制回归直线。

2.3 简单线性回归分析中与t检验有关的结果

【SAS主要输出结果及解释】

以上是例1中数据的简单线性回归模型参数检验的结果，采用t检验。例1共20例数据，所以截距β0的检验统计量t0和斜率β1的检验统计量t1均服从自由度为18的t分布。β0的最小二乘估计值=-2.06406，的标准误差，β0的检验统计量t0=-1.63，t0对应的P值为0.1196，所以截距β0与0之间差异无统计学意义。β1的最小二乘估计值，的标准误差，β1的检验统计量t1=9.9，t1对应的P值小于0.0001，故斜率β1与0之间差异有统计学意义。由于截距β0与0之间差异无统计学意义，所以回归方程的截距项β0为0，从而应重新拟合下面的回归方程：

【SAS主要输出结果及解释】

以上是根据调整后的过程步可以得到的简单线性回归参数检验的结果（删除截距项），t1=47.68，P＜0.0001，所以斜率β1与0之间差异有统计学意义，故由例1中数据得到的线性回归方程为y^=0.02626x。图1是用该数据生成的散点图以及根据回归方程拟合的回归直线。

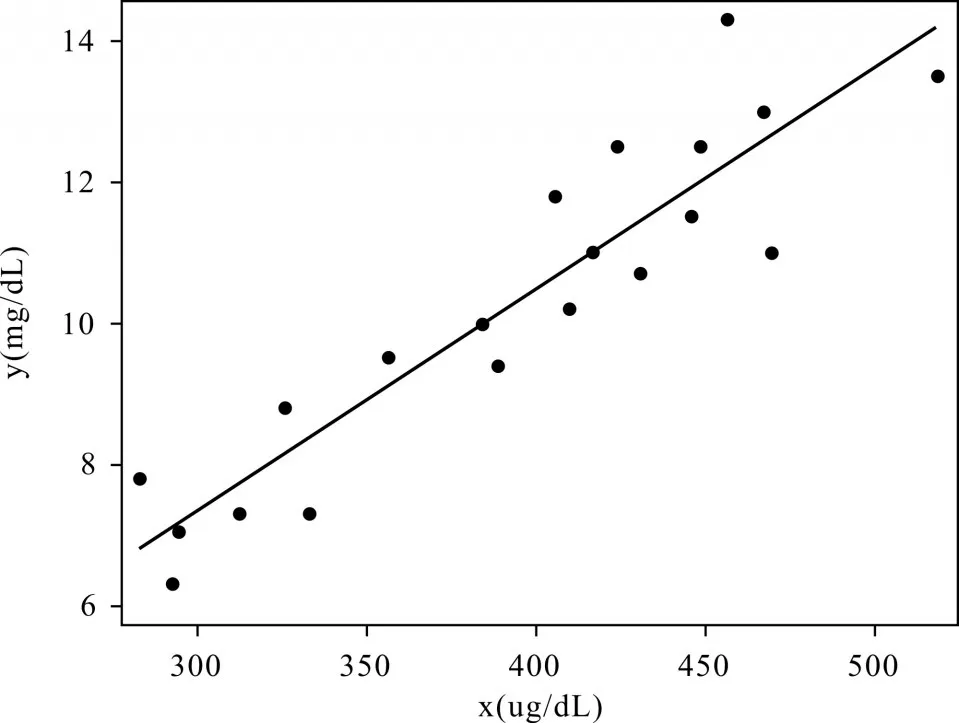
图1 （x，y）散点图及拟合的回归直线

3 多重线性回归模型的参数与0之间差异t检验的实例

3.1 多重线性回归分析的数据结构

【例2】研究26例糖尿病患者的血清总胆固醇（x1）、甘油三酯（x2）、空腹胰岛素（x3）、糖化血红蛋白（x4）与空腹血糖（y）之间的关系［6］。数据见表2。

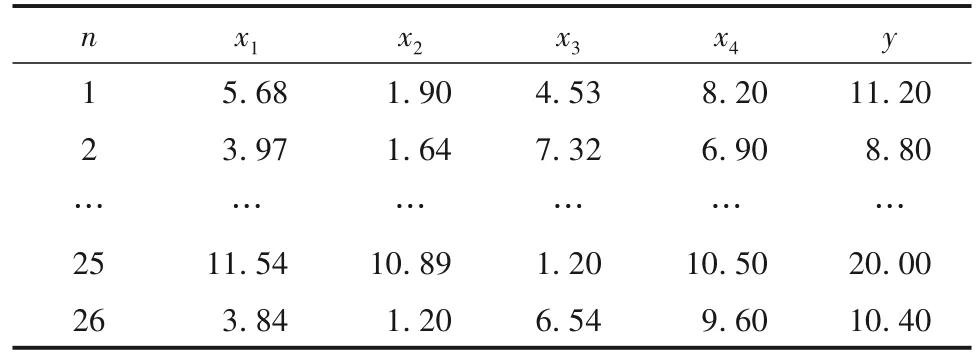
表2 26例糖尿病患者血样中相关指标测定结果

通过t检验来判断多重线性回归模型中的总体截距和各个自变量对应的系数与0比较是否存在统计学差异，从而判断各个自变量是否有意义。本研究中，将空腹血糖设为因变量，将血清总胆固醇、甘油三酯、空腹胰岛素和糖化血红蛋白设为自变量。

3.2 构建与求解多重线性回归模型的SAS程序

根据例2的数据进行多重线性回归分析，并对回归方程的各参数进行t检验。

SAS程序如下：

【程序说明】以上SAS程序由3步构成（实际使用只需要第1步和第3步），包含1个数据步和2个过程步。数据步建立例2中的数据集test2，输入26例糖尿病患者血清总胆固醇（x1）、甘油三酯（x2）、空腹胰岛素（x3）、糖化血红蛋白（x4）和空腹血糖（y）的数据。第一个过程步调用REG过程，但本过程没有采用变量筛选，因此即使某个变量不具有统计学意义也会被纳入多重线性回归模型。第二个过程步也调用了REG过程对回归方程进行总体检验和参数检验，但为了避免多重共线性，该过程步采用逐步回归法（stepwise）进行变量筛选，只有具有统计学意义的变量会被纳入多重线性回归模型。

3.3 多重线性回归分析中与t检验有关的结果

【SAS主要输出结果及解释】

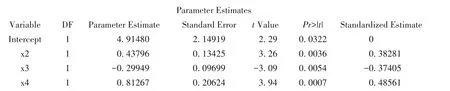
以上是例2中数据进行多重线性回归分析的参数检验的结果（采用变量筛选），采用的是t检验。例2包括26例数据，经变量筛选后只留下3个自变量，故βj的检验统计量tj均服从自由度为22的t分布。自变量血清总胆固醇（x1）在变量筛选过程中被剔除。总体截距β0对应的检验统计量t0=2.29，P=0.0322，说明β0与0之间差异有统计学意义；甘油三酯（x2）的系数β2对应的检验统计量t2=3.26，P=0.0036，说明β2与0之间差异有统计学意义；空腹胰岛素（x3）的系数β3对应的检验统计量t3=-3.09，P=0.0054，说明β3与0之间差异有统计学意义；糖化血红蛋白（x4）的系数β4对应的检验统计量t4=3.94，P=0.0007，说明β4与0之间差异有统计学意义。总体截距和三个自变量的回归系数与0之间差异都有统计学意义，多重线性回归方程如下：

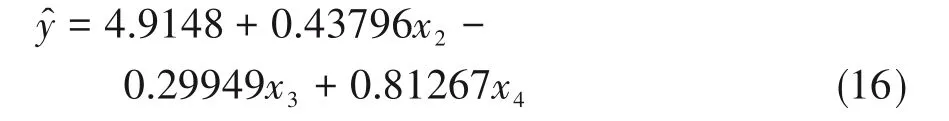
4 讨论与小结

4.1 讨论

常规t检验（定量资料均值比较）在SAS中是用TTEST过程步实现。而本文是通过SAS中的REG过程对简单线性回归模型和多重线性回归模型中参数与0之间的差异进行t检验。若自变量的回归系数与0之间差异无统计学意义，则说明该自变量对因变量的影响可忽略不计；反之，则说明该自变量对因变量的影响有统计学意义。此外，还需对截距项与0之间的差异进行t检验，若检验结果为差异无统计学意义，则构建的回归方程中截距项为0。进行线性回归分析时应注意：①数据应满足使用线性回归分析的前提条件；②与0之间差异无统计学意义的参数可以在SAS程序中使用相应的语句进行调整，使其不出现在最终构建的线性回归方程中。