如何正确运用t检验——相关系数与0比较t检验及SAS实现

2020-09-09宋德胜刘媛媛李长平胡良平

四川精神卫生 2020年4期

宋德胜，刘媛媛，李长平，2，崔壮，胡良平

（1.天津医科大学公共卫生学院，天津 300070；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3.军事科学院研究生院，北京 100850*通信作者：胡良平，E-mail：lphu927@163.com）

相关分析的目的是揭示两个变量之间是否存在线性相关性。目前较常见的两个随机变量之间的相关性度量指标是Pearson乘积矩相关系数，简称Pearson相关系数，其公式表示的是实际数据与期望数据的偏离程度［1］。与Pearson相关系数不同，Spearman秩相关系数和Kendall's tau-b秩相关系数利用了秩。这两种秩相关系数一般是当资料不满足Pearson相关系数时的替代方法。从几何学角度看，Pearson相关系数测量的是两个定量变量之间呈线性相关的程度；而两种秩相关系数则不限于线性相关。但三者具有类似的性质：①相关系数的范围都是［-1，1］；②都具有对称性。值得注意的是，不管是正相关还是负相关，都不涉及“因果关系”。本文对这三种相关系数的概念、作用以及应用进行介绍。

1 基本原理

1.1 Pearson相关系数与0比较t检验

Pearson乘积矩相关系数由Karl Pearson提出［2］。它是两个定量变量相关的一种参数化测量，既可计算相关强度，也可得出相关方向。若两个定量变量呈完全正线性相关，则Pearson相关系数为1；若两个定量变量呈完全负线性相关，则Pearson相关系数为-1；若两个定量变量不呈线性相关，则Pearson相关系数为0。因此，Pearson相关系数的取值范围为［-1，1］。此外，Pearson相关系数要求两个定量变量服从二元正态分布、两个定量变量每一对取值应来自同一个个体，且所有受试对象应抽自满足“同质性”的同一个总体。若不满足这些前提条件，则不适合计算任何相关系数；仅当不满足“双变量正态分布”时，可考虑进行秩相关分析。Pearson相关系数计算公式如下：

一般来说，上述统计量来自于样本，若需推论到总体，则需要进行假设检验。经统计学家证明，Pearson相关系数服从自由度为n-2的t分布。检验统计量t的计算公式如下：

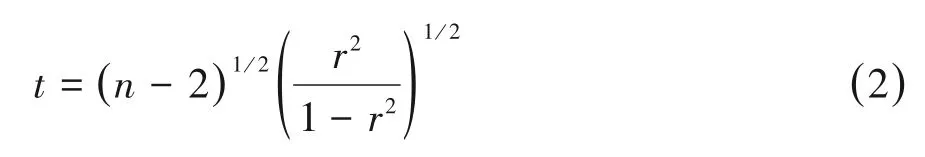
上式中，r是来自样本的Pearson相关系数。

1.2 Spearman秩相关系数与0比较t检验

Spearman秩相关系数是Charles Spearman提出的一个一般非参数统计量，通常用rs表示［3］。它使用单调函数度量两个变量的关系。与Pearson相关系数类似，Spearman秩相关系数的取值范围也为［-1，1］。实际上，Spearman秩相关系数等同于两个变量秩次值的Pearson相关系数，既可以用于连续型随机变量，也可用于离散有序随机变量。计算公式如下：

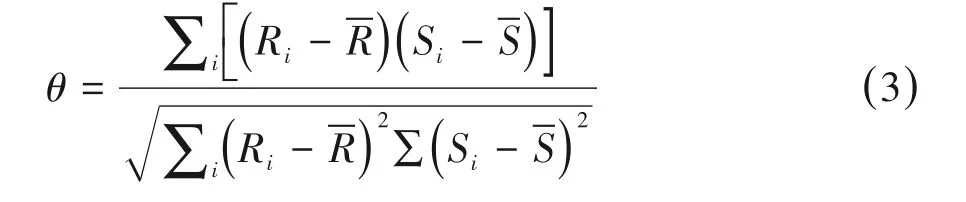
上式中，Ri是xi的秩次，Si是yi的秩次，是Ri的均值，是Si的均值。若存在结（即同一个变量的原始数据中存在2个或2个以上相同的数据），则使用平均秩。

对来自于样本的Spearman秩相关系数仍需假设检验才可以推广到总体。Spearman秩相关系数仍服从自由度为n-2的t分布。检验统计量t的计算公式如下：

1.3 Kendall's tau-b秩相关系数与0比较Z检验

Kendall's tau-b秩相关系数也称为Kendall'sτ系数，是用于测量两个观测指标之间秩相关的指标，由Maurice Kendall提出，可用于衡量配对设计扩大条件下两属性变量等级之间的相关程度［4］。本质上，两个变量之间秩的分布越相似，则Kendall's tau-b秩相关系数越大，它也是一种一般的非参数统计量，因为它不依赖于两个变量的分布。由于Kendall's tau-b秩相关系数对结进行了处理，因此，其取值范围为［-1，1］。Kendall's tau-b秩相关系数计算公式［5］如下：

Z服从标准正态分布。其中，

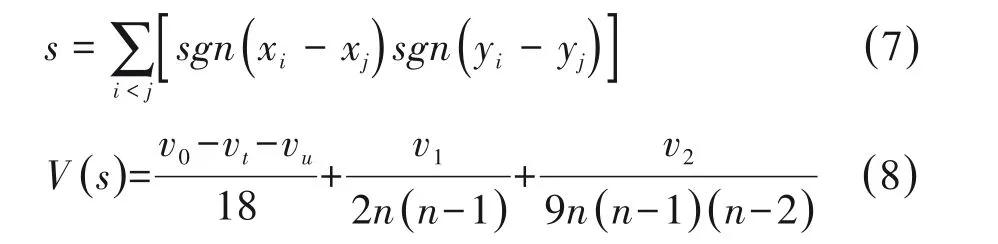
在这里，

2 实例

2.1 Pearson相关系数r与0比较t检验

【例1】本例数据为N.C.State University关于男性身体健康课程的调查数据。数据集变量包括年龄（岁）、体重（kg）、跑步时长（跑步1.5英里所需时间，按分钟计）以及氧摄入量［mL/（kg·min）］。试分析氧摄入量与跑步时长之间的关系。资料见表1。

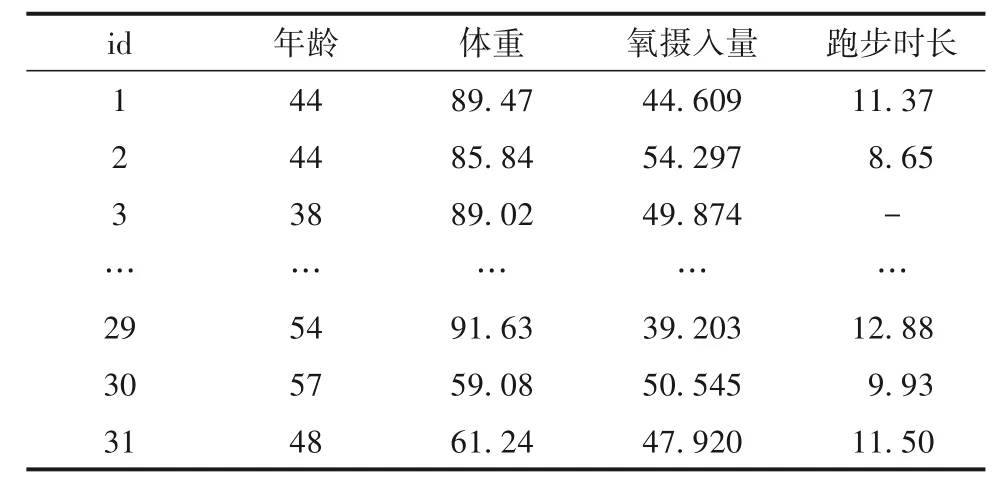
表1 男性身体健康调查数据

2.1.1 创建数据集

2.1.2 绘制氧摄入量与跑步时长的散点图

【程序说明】SGPLOT过程是SAS软件中的绘图过程。Scatter语句表示绘制散点图。之后的“x=”和“y=”分别指定需要绘制散点图的两个变量。运行结果见图1。

图1 Oxygen（氧摄入量）和Runtime（跑步时长）的散点图

由图1的散点图可知，Oxygen和Runtime之间大致呈线性负相关。也就是说，随着氧摄入量的增加，跑步到1.5英里所需时间逐步减少。因此，可以进行相关分析。

2.1.3 相关分析

【程序说明】本例调用SAS软件中的CORR过程进行相关性分析。CORR过程语句后的data选项指定包含相关分析变量的数据集，pearson表示计算Pearson相关系数（若此处不指定任何相关系数，默认显示Pearson相关系数）。VAR语句指定需要进行相关分析的变量。

【SAS主要输出结果及解释】

输出结果中，首先给出了两个变量的一些简单统计描述结果，接着给出了Pearson相关系数及其假设检验结果。Pearson相关系数分析结果的右上方由上到下分别是样本Pearson相关系数、对Pearson相关系数进行假设检验对应的P值以及排除缺失值后用于分析的样本例数。可以看到，在本例中，氧摄入量和跑步至1.5英里所需时间呈负相关（相关系数为-0.86843），且t检验的P值小于0.0001，因此可认为随着氧摄入量的增加，跑步至1.5英里所需时间呈线性下降趋势。说明：输出结果中未给出检验统计量t的数值。

2.2 Spearman秩相关系数rs及与0比较t检验

【例2】某研究机构收集了成年人年龄和身体脂肪百分比的数据，本例选取了其中18例数据。分析年龄与身体脂肪百分比的关系。见表2。

表2 18名成年人年龄和身体脂肪百分比数据

2.2.1 创建数据集

2.2.2 绘制散点图

【程序说明】与例1类似，绘制年龄与身体脂肪百分比的散点图见图2。

图2 年龄（Age）与身体脂肪百分比（Bodyfat_perc）散点图

由图2可知，年龄与身体脂肪百分比线性趋势不明显，因此，本例将使用Spearman秩相关分析。

2.2.3 秩相关分析

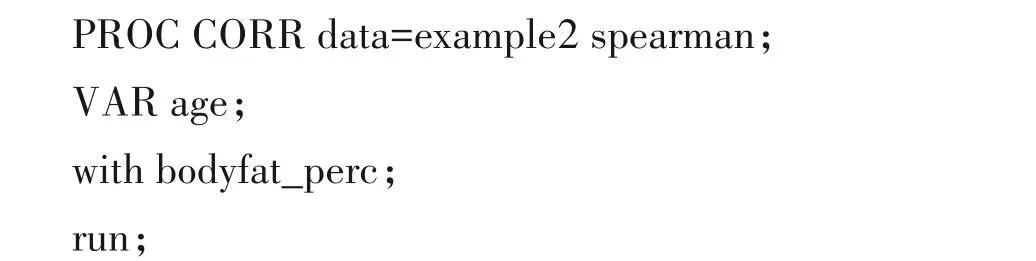
【程序说明】本例也使用PROC CORR调用SAS软件的CORR相关分析过程。过程语句后的Spearman选项表示进行Spearman秩相关分析。VAR语句指定要分析的变量，with指定另一个需要分析的变量。

【SAS主要输出结果及解释】

由结果可知，年龄和身体脂肪百分比的Spearman秩相关系数为0.75388，P值为0.0003，由此可认为，随着年龄的增加，身体脂肪百分比也在上升。

说明：由于对Kendall's tau-b秩相关系数的假设检验是Z检验（即以正态分布为理论依据的检验），不是t检验，超出了本文的范围，故从略。值得一提的是：适合采用Kendall's tau-b秩相关分析的数据结构为“配对设计扩大形式的定性资料”，可参阅文献［6］了解其方法及应用，此处从略。

3 讨论与小结

3.1 讨论

Spearman秩相关系数通常适用于单组设计双变量且资料不符合Pearson相关分析的前提条件的场合，由于它是基于“秩次”计算得到的秩相关系数，故其精确度会有所降低。

Pearson相关分析对资料的要求很高，通常要求资料为单组设计二元定量资料且两变量呈线性变化趋势。但在实际使用中，前提条件可能会略有偏移，但应注意不能偏离过大。如张美燕等［7］利用其分析了精神科门诊患者使用四种量表评定之间的关系。

Kendall秩相关系数有三种，分别是Kendall's tau-a［8］、Kendall's tau-b 和 Kendall's tau-c［9］秩相关系数。本文主要探讨的是Kendall's tau-b秩相关系数，它与其他两类Kendall秩相关系数的主要区别在于对结的处理方法不同。因篇幅所限，详情从略。