如何正确运用t检验——两算术均值比较优效性t检验及SAS实现

2020-09-09姚婷婷李长平胡良平刘媛媛

四川精神卫生 2020年4期

姚婷婷，李长平，2，胡良平，马骏，刘媛媛 *

（1.天津医科大学公共卫生学院，天津 300070；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029；3.军事科学院研究生院，北京 100850*通信作者：刘媛媛，E-mail：ivyuan10@126.com）

在进行成组设计一元定量资料两总体均值之间的比较时，传统差异性检验的零假设为两个总体均值相等，其统计推断往往仅限于两者的差异是否有统计学意义。基于给定的显著性水平α，若P＞α，意味着统计上“不能拒绝零假设”，但并非说明零假设（两均值相等）一定成立；若P≤α，虽然可“拒绝零假设”，但也只能推断两者之间的差异在统计学上是认可的，而不能评价其差异的大小。在临床上，新药临床试验的开展越来越多，由于差异性检验不能准确区分两种药物疗效差异的方向性并体现差异大小所代表的临床实际意义，于是，优效性检验、等效性检验和非劣效性检验被提出并广泛应用［1-2］。本文主要介绍临床试验中优效性检验的相关内容，包括优效性检验的概念、假设检验的原理、样本量的估计和界值的确定，再结合临床实例，介绍两算术均值比较优效性t检验及SAS实现。

1 概述

1.1 优效性检验简介

优效性检验的主要目的是检验试验药的治疗效果是否优于对照药（安慰剂对照或阳性对照）。对于尚未上市的药品，无论是创新药还是仿制药，以安慰剂作为对照时，应证实其优效性［2］；选择已上市的同一治疗领域的药物作为阳性对照药时（阳性药物的选择应考虑阳性对照药有效性的既有证据和阳性对照药物效应的稳定性［3］），当预试验的结果表明试验药的效果不仅比对照药效果好，而且两者之间效应指标的差量在数量上相当可观，结合临床专业知识可知，此差量具有临床上的实际意义，此时为了通过正式临床试验，显示试验药的治疗效果优于对照药，可选用优效性检验［4］。在试验设计阶段需要设定一个界值δU来界定试验药的优效性。δU取正值，表示“方向”，即当疗效指标为高优指标时，试验药的效应指标的取值大于阳性药的效应指标的取值，这是一个单侧检验。

1.2 优效性设计下两均值比较的假设检验

对两均值比较的优效性试验，若评价指标为高优指标，如生存时间，即均值越大表明疗效越好，其相应的检验假设如下。

无效假设H0：μT-μR≤δU（两种药物疗效相等或试验药劣于对照药）

备择假设H1：μT-μR＞δU（试验药优于对照药）

对两均值比较的优效性试验，若评价指标为低优指标，如疾病持续时间，即均值越小表明疗效越好，其相应的检验假设为：

无效假设H0：μR-μT≤δU（两种药物疗效相等或试验药劣于对照药）

备择假设H1：μR-μT＞δU（试验药优于对照药）

其中，μT为试验组总体均值，μR为对照组总体均值，δU为优效性界值，当δU为0时，分析方法与差异性检验相同。

以下基于“高优指标”的前提，给出成组设计一元定量资料两均值比较时优效性检验所需要的t检验统计量：

在实际应用中，还可采用置信区间法检验，它是分析时最直接的方法，且相比于假设检验可提供更多的信息。对于两个均值比较的优效性检验，按单侧（1-α）%的置信度，计算单侧置信区间下限CL，公式如下：

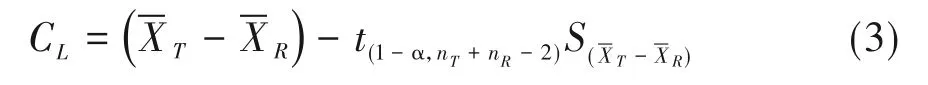
若（CL，∞）不包括δU，即CL＞δU，可以得出试验组疗效优于对照组的结论［5］。

1.3 优效性界值δU的设定

从临床意义上确认药物的疗效，界值的确定不可缺少。在优效性试验中，界值是指试验药与对照药之间相差的临床上认可的最小值［6］。优效性试验中仅用一个界值，界值的确定必须在试验设计阶段完成并在试验方案中阐明，若有修订，必须在揭盲之前进行并陈述理由。

在确定界值时，若δU太小，将可能把疗效远不如对照药的药物判断为优效或等效；若δU太大，则可能将本来可推广应用的比对照药更有效的药物误判为无效而得不到及时上市。但在实践中界值的确定往往较复杂，需根据已有的文献资料、设计类型及数据的分布类型，从临床认识水平及成本效益等多方面综合考虑，将统计学推理和临床判断相结合［2］。

1.4 优效性检验样本含量的估计

两均值比较的优效性临床试验样本量大小与两组均值、标准差、优效性界值、I类错误和II类错误大小以及两组例数分配比例有关。两组均值相差越小，所需样本量越大；优效性界值越大，所需样本量越大；所设定的允许犯的I类错误和II类错误越小，所需样本量越大［7］。对于两均值比较的优效性试验，对照组样本量估计公式如下：

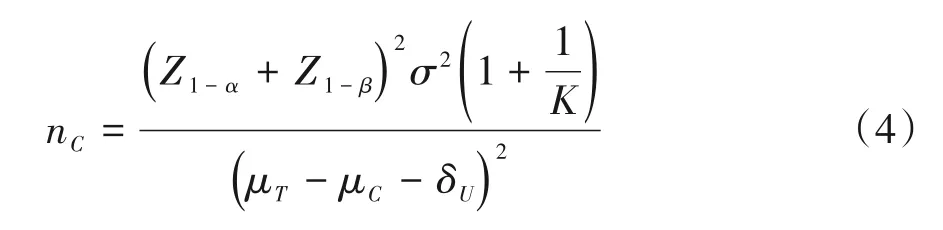
上式中，μT和μC分别为试验组和对照组均值，σ为标准差（假设两组标准差相同）；α和β分别为犯I类错误和II类错误的概率；K为试验组与对照组例数分配比，可根据估计的对照组样本量和分配比例K获得试验组样本量。

试验中，还应考虑资料质量、患者依从性等问题，若受试者脱落，应在实际临床试验操作中扩充一定的病例数来校正估计实际的样本含量。

2 实例分析

2.1 基于“样本含量、均值和标准差”进行优效性检验

【例1】比较泮托拉唑与奥美拉唑对消化性溃疡出血患者止血的效果［8］。将80例消化性溃疡出血患者随机分为泮托拉唑组和奥美拉唑组，记录两组患者的出血停止时间，评价泮托拉唑对消化性溃疡出血患者止血的效果是否优于奥美拉唑（假定：经临床专家商定，优效性界值取0.6 d）。数据见表1。

表1 泮托拉唑组与奥美拉唑组的出血停止时间（d）

该资料为成组设计一元定量资料，目的是评价泮托拉唑对消化性溃疡出血患者止血的效果是否优于奥美拉唑，并设定了优效性界值，这时采用优效性检验。本例中，评价指标为出血停止时间，数值越小表明疗效越好，故评价指标为低优指标。

SAS程序如下［9］：

【程序说明】在以上SAS程序中，下标为“2”的代表对照组；由于评价指标为低优指标，故在计算t检验统计量时，公式（1）的分子上两算术均值的顺序要互换一下。第1步定义样本含量、两组样本均值、样本标准差和优效性界值；第2步计算两组样本均值的离均差平方和；第3步计算两组的合并方差和两样本平均值之差的标准误；第4步进行假设检验，计算检验统计量t值、P值；第5步计算均值差值单侧置信区间下限CL；PRINT过程步输出计算结果。

【SAS主要输出结果及解释】

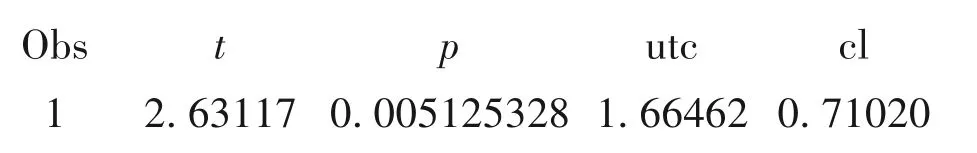
统计与专业结论：t=2.63117，P=0.005125328，按照α=0.05（单侧检验），拒绝H0，接受H1，可以认为泮托拉唑对消化性溃疡出血患者止血的效果优于奥美拉唑。从95%置信区间下限来看，CL=0.71020＞0.6，可以认为泮托拉唑对消化性溃疡出血患者止血的效果优于奥美拉唑，该结论与假设检验结果一致。

2.2 基于原始定量数据

【例2】沿用例1中的信息，根据样本均值、标准差模拟出与例1中样本含量相同的随机数。评价泮托拉唑对消化性溃疡出血患者止血的效果是否优于奥美拉唑（假定：经临床专家商定，优效性界值取0.6 d）。

SAS程序如下：

【程序说明】第一步，根据例1中的样本均值、标准差产生两组服从各组对应样本均值、标准差的正态分布的随机数，通过seed设置种子数，使模拟数据具有重现性；第二步，在TTEST过程中，“sides=u”表示采用上单侧检验，“h0=0.6”为设定的优效性界值；“alpha=0.10”代表求均值之差的双侧90.0%置信区间，相当于单侧95.0%置信区间。由于评价指标为低优指标，故将试验组设为第二组（group2），对照组设为第一组（group1）。

【SAS主要输出结果及解释】

以上结果分别为两组出血停止时间的均值以及它们差值的均值、标准差、标准误、双侧90.0%（相当于单侧95.0%）置信区间等信息。

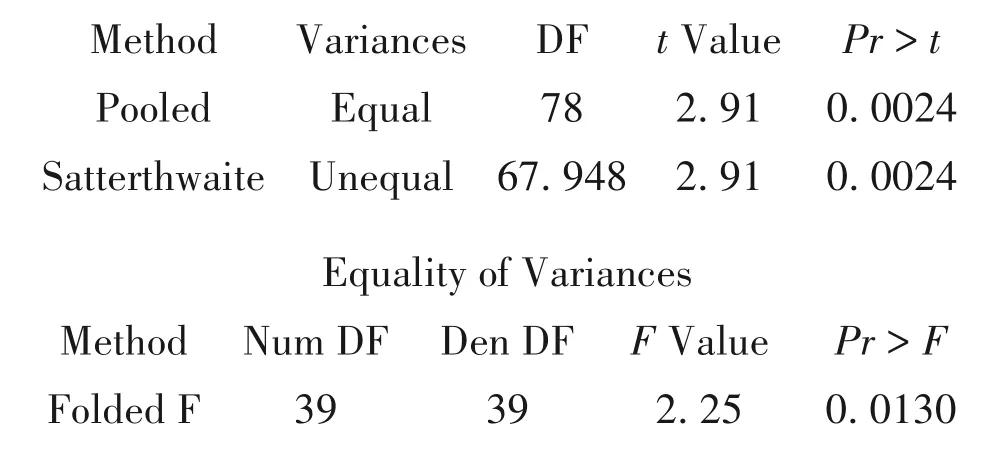
根据方差齐性检验的结果（EqualityofVariances），F=2.25，P＜0.05，认为两总体方差不等。对应的t检验结果中，应该参照Satterthwaite方法。

统计与专业结论：t=2.91，P=0.0024，按照α=0.05（单侧检验），拒绝H0，接受H1，可以认为泮托拉唑对消化性溃疡出血患者止血的效果优于奥美拉唑。从95%置信区间下限来看，CL=0.7612＞0.6，可以认为泮托拉唑的效果优于奥美拉唑，该结论与假设检验结果一致，即可以认为泮托拉唑对消化性溃疡出血患者止血的效果优于奥美拉唑。

3 讨论与小结

3.1 讨论

基于不同的研究目的，临床试验有不同的类型，而且试验类型必须在试验设计阶段确定。然而，实际工作中有些情况完全确定下来并不容易，例如对新产品的研发定位如果在疗效上有足够的信心认为试验药优于阳性对照药，则可直接采用优效性试验；如果新产品的疗效与阳性对照药比较并无明显优势，但有足够的信心认为疗效相差处于临床可接受范围，关键是有其他方面的明显优势，这时可选择非劣效性试验。如果对试验药疗效的优势把握不大，一般不适合贸然设计为优效性试验，可考虑先设计成非劣效性试验，如果试验结果经过统计分析（前提是基于临床认可的优效性界值）能显示出优效性，则可按优效性下结论，具体见文献［10-11］。若按照优效性试验设计，而没有得出优效性结论，则通常不再考虑进行非劣效推断，毕竟在优效性试验设计时一般不会考虑非劣效界值的问题，如果事后确定非劣效界值将会引入偏倚，导致I类错误膨胀［11］。