适应性FCM聚类分析对导轨温度特征的改进研究

李志伟

（四川建筑职业技术学院，四川 德阳618000）

关键字：适应性FCM聚类算法；导轨；温度测点；改进研究

0 引 言

机床导轨热特性研究的关键是其温度测点改进设计，通常在进行导轨热变形补偿分析前，要对其进行环境温度与变形检验，并以此为依据建立相应的热变形误差模型[1-2]。由于导轨工作时易受到外部环境及参数变化的影响，其温度场具有时变性。为了解导轨温升和热变形情况，需在导轨相应位置设置温度传感器，但考虑成本和导轨的工况，以及相应建模时处理数据量较多等情况，同时在导轨上安装过多温度测点会使各测点产生干涉现象降低预测精度，所以必须先对导轨的温度测点进行合理分组分析，以增强模型预测的准确性[3]。

采用适应性FCM聚类算法改进温度测点时，需保证选择关键参数的真实性，选取样本分类数c及加权指数m作为关键参数[4-5]。在分析中要确保c的准确，以至于确定聚类数有效性，m对分析模型目标函数的敛散性及一致性有关键联系。加权指数m取3具有较好的收敛性，但聚类数C在不同情况下存在一定的随意性，为了保证分析结果的准确性，需对聚类数C的选取进行改进优化[6]。

1 适应性FCM算法分析与建模

普通的FCM聚类算法对机床温度测点优化，一般算法中的设置分类数需人为设定，由于经验及其他因素的影响，将导致分析结果出现较大的偏差，同时分析结果的有效性需依赖有相关工程经验的专业人员进行判断，耗时耗力[7]。

进行分类的目的是将数据集合进行分组，同时需保证各组间的间距要大，而每组数据个体间的间隔尽可能小。按照该方法，为保障分析结果的准确性，需对FCM聚类算法进行适应性改进，调整后的聚类数C的自适应函数为

分析得出，改进后的适应性函数L（c）的分母为组间距，分子为各组内数据点间的间距，由此得出结论：L（c）的值越大，则分类越准确，相应的分类数也越有效。由于导轨的运行参数为常规空载条件运行，其他系统保持不变，当导轨在工作状态时，设置X向移动速度为2 mm/min，工作时间为1 h, 再梯级递进移动的试验方案，相应每隔300 s采集一次数据。其他条件保持不变，当加权指数m取值为3，即可保持良好的一致性。以传统算法为理论基础，得到聚类数C的自适应函数如下：

1）理论初始计算条件：设置迭代收敛条件ε≥0，原始分类数目c=1，当分类数c为1时,自适应值L（c）=1，相应原始分类矩阵v（0）,同时计数器b归零。

4）用一个矩阵范数||·||比较vk和v（k+1），若｜|v（k+1）－vk||≤ε，则迭代终止，否则，设b=b+1，转向步骤1）继续迭代，直至满足要求。

5）计算L（c），若自适应函数满足L（c-1）≤L（c-2）且L（c-1）≥L（c），即自适应分类结束，否则，设c=c+1，转向步骤1）继续迭代，直至满足要求。

2 适应性FCM聚类算法在导轨温度测点改进分析实例

适应性FCM聚类算法，能自动对机床导轨温度测点进行建模仿真并合理优化分组，且分类结果准确，在实际的应用中具有一定的前景。

为了能够对导轨的温度测点进行准确分析，在实际研究中将该算法应用于导轨的温度测点优化。通过ANSYS对导轨瞬态热变形仿真建模分析基础上，根据研究的具体情况调整分析过程，以导轨在工况空载条件下的瞬态温度场及热变形状况为研究对象，并布置若干测点以实时监测温度，方便准确获取监测点的温升与热变形状况，测点分布位置导轨上端1、左端2、右端3、前端4、后端5，如图1所示。

为确保试验有效，导轨采用移动速率递进方式进行工作，前1 h内移动速率为2 mm/min，然后在速率为2.5 mm/min 继续工作1 h，同时每间隔300 s采集一次测点的试验数据，当前温度为室温20 ℃。为了保证各测点的时效性及准确性，对各测点的状态进行分析得到相应的时频图，如图2 所示。

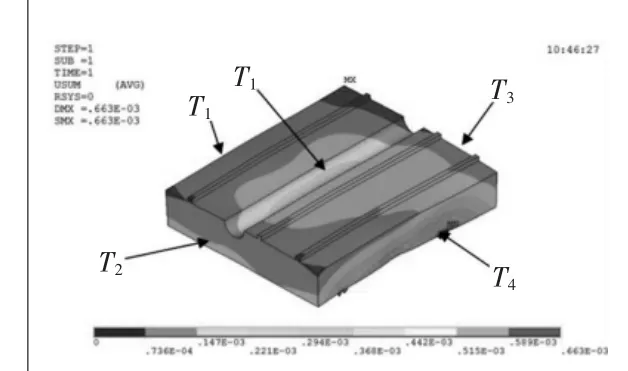
图1 测点分布位置图

图2 自适应函数的时频图

通过时频图分析，各测点温度能量值响应灵敏（测点能量值单位为℃），监测的温度准确有效，能够反映真实加工状态，基于适应性FCM聚类改进算法对导轨温度测点实施分组优化，m取3，当C取3类时，试验终止，L（c）计算值如下：L（2）=331.437，L（3）=398.385，L（4）=353.012，L（5）=326.253。L（c）的变化过程如图3所示。满足理论设定条件，经分析分组为3类时分析结果最佳，结果越准确。同时得到各测点的实时监测温度，如表1所示。

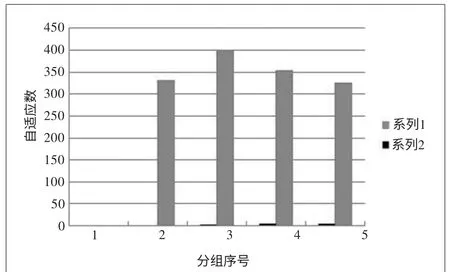
图3 适应性分组数分布柱状图

为了保证导轨测点分组的准确性，需计算各测点的可靠性，通过建立测点的可靠性计算模型，设传递变量为对数函数，将测点温度作为学习样本，利用高斯函数，设k为迭代步数，当k次迭代的阈值中心为u1（k）、u2（k）、…、un（k），对应的域为φ1（k），φ2（k）、…、φn（k）。计算步骤为：

1）计算参数输入和阈值中心的间距‖yj－Ui（k）‖。其中：i=1，2，…，n；j=1，2，…，m。

2）参数样本yj，以最小间距法则对应分组。

3）重置新的阈值中心：

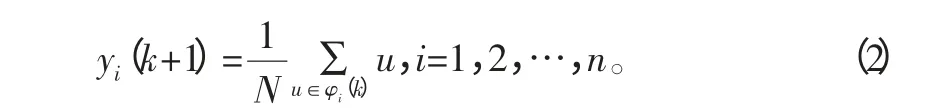
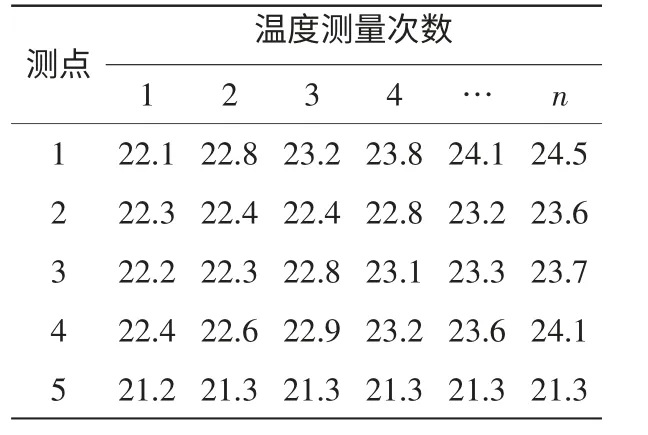
表1 测点温度数据 ℃

其中：N为第i个阈值范围φi（k）中含有的参数。

4）当yi（k+1）≠yi（k），重回步骤1），否则计算终止。

6）用Matlab语言对温度测点进行关联度模拟。

由上述过程，建立了导轨温度测点的可靠性模型，通过步骤1）～6）计算得到对应测点的可靠度R（i,j）。温度测点的可靠性模糊分组矩阵如表2所示。

根据之前的分析结果，确定将所有测点分成3组。通过对比有用测点的数据，确定选择第3类测点的可靠性数据，并按照数据关联度重新对各测点进行分组归类。第一组：1#；第二组：2#、3#；第三组：4#、5#。

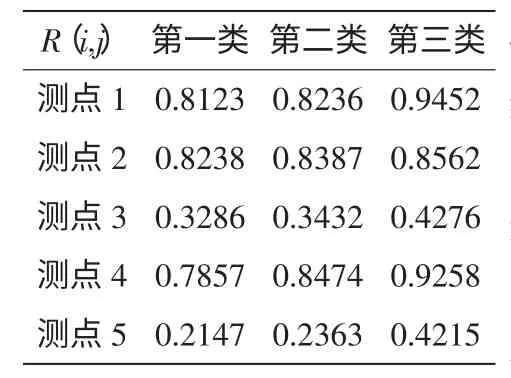
表2 温度测点的可靠性模糊分组矩阵

同时利用相关系数法挑选每组中一个重要测温点作为温度测点研究，由表2按测点的可靠性系数，得到各测点间的关联系数如表3所示，最终取1#、2#、4#测点为导轨的关键测点。

3 结 论

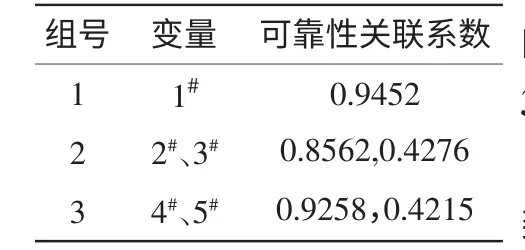
表3 导轨温度测点的相关系数表

本文采用适应性FCM聚类分析算法对导轨测点进行改进分析，其原理为依据导轨温度及热变形量，增设聚类数C的适应性目标函数，建立相应的适应性FCM聚类分析算法可靠性模型，通过建模得到多元回归关键测点热误差分析数据。为了得到准确的温度测点，将聚类数自适应算法施加到导轨的测温点改进上，将导轨的关键测点由5个减少到3个。实践证明，该算法不仅能给出最佳聚类数，还能对测点进行分组优化，其测点分类情况与实际情况更加吻合。该方法为机床温度测点可靠性分析研究开辟了新的途径，具有广阔的应用前景。