基于响应曲面的悬臂支架设计优化

2020-09-08吉海云李艳军曹庆宇秦峥嵘刘元周

机械工程师 2020年8期

吉海云，李艳军，曹庆宇，秦峥嵘，刘元周

（中国航发沈阳发动机研究所，沈阳110015）

0 引言

悬臂支架是露天试车台的框架及基础，是整个试车台的硬件基础，也是试车台重要的组成部分之一。

悬臂支架不但要承受发动机的推力和发动机的重力，还要承受安装在其下的测量台架、预安装架、发动机吊装系统等的重力。因此悬臂支架设计的优劣直接关系到整个台架推力测量的准确性。本文采用实验设计方法（DOE设计）中的响应曲面对悬臂支架的各参数进行优化，从而得到各参数最优解。本文利用ANSYS软件对悬臂支架进行仿真计算，结合实验设计方法对影响悬臂支架变形量的影响因子进行敏感度分析和设计方案优化[1]。

1 悬臂支架结构

悬臂支架主要包括立柱、横梁、水平焊接架、转接架及其配套的钢座基础、楼梯、钢平台等，发动机的推力和重力通过预装架传递给测量台架，测量台架传递给转接架、水平焊接架，再通过水平焊接架传递给横梁、立柱，最后传递给钢座基础再传给土建。悬臂支架的组成如图1所示。

2 实验设计（DOE设计）简介

实验设计（DOE设计）是对实验进行合理安排，以较小的实验次数、较短的实验周期和实验成本，获得理想的实验结果[2]。实验设计考虑了各个因子对响应的影响，基于现有数据通过统计分析方法找出恰当的数学表达式来拟合响应，从而建立起各因子与响应之间系统模型，并对各参数的未知输入值进行预测和择优。

响应曲面（RSM）是以实验设计为基础的用于多变量建模与分析的一套统计处理技术[3]。利用已知的实验数据拟合出响应与各参数之间的函数关系，通常采用简单的二阶多项式响应曲面（PRS），表述为

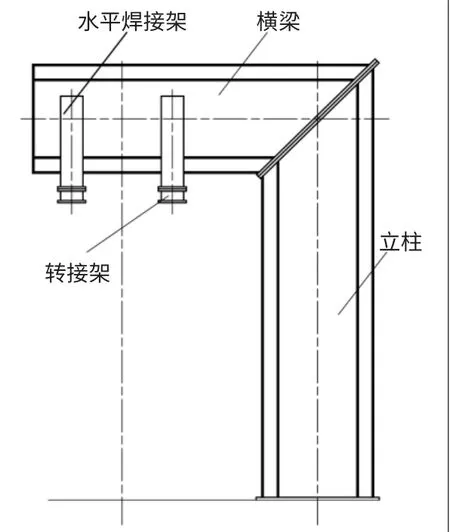
图1 悬臂支架组成

式中：y为响应；x为因子；C为多项式系数；ε为随机误差；n为因子的维数。

工程上使用上述多项式即可满足精度的要求，因此该次优化也采用这种形式的二阶多项式。

3 实验方案确定

3.1 实验指标

因悬臂支架对变形量控制要求非常严格，而支柱和横梁对整个悬臂支架变形量贡献最大，因此本文主要针对这两部分进行优化从而确定最佳的设计参数。以立柱和横梁的变形量为主要响应，应力为次要响应。

3.2 实验因子

立柱与横梁采用相同的双层盒式结构，同时在两层中间增加加强筋来控制变形量，因此选择外筒直径、外筒壁厚、内外筒间距、内筒壁厚、加强筋数量和加强筋壁厚6个参数为实验设计因子，每个因子两水平，如表1所示。

表1 因子水平表

3.3 实验设计

采用正交实验能够显著减少实验次数，利用Minitab建立六因子全因子响应曲面的实验设计，其中立方区组数1，选择表面中心点，共有77组需要计算的数据。

3.4 仿真模拟实验

3.4.1 计算参数确定

以发动机排气方向为-X方向，以立柱向横梁方向为-Y方向，重力方向为-Z方向，+X方向受力为600 kN，-Z受力650 kN，-Y方向的弯矩为2623.5 kN·m。

3.4.2 仿真模型建立

对悬臂支架进行简化，只建立包含立柱、横梁及水平焊接架的模型，水平焊接架采用相同的结构形式及参数，立柱与横梁各参数按照实验计划使用UG建立简化模型。

3.4.3 网格划分与边界条件

使用ANSYS Workbench中的Static Structural模块中集成的网格划分软件划分网格，网格采用非结构化网格，网格单元总数约50万个。

以立柱底面法兰为固定约束，所受力及弯矩加载在水平焊接架底面的两个法兰处。

3.5 仿真结果

经过仿真计算得到77组变形量和应力，部分计算数值如表2所示。

表2 部分计算结果

4 变形量分析与优化

4.1 响应影响分析

将仿真计算得到的每个模型的最大变形量和最大应力输入到Minitab软件中的工作表中。

4.1.1 主效应分析

外筒直径在高水平时各响应的平均值为Ah=4.695 mm，外筒直径在低水平时各响应的平均值为Al=7.377 mm，外筒直径的主效应为Am=Ah-Al=-2.682 mm。

外筒壁厚在高水平时各响应的平均值为Bh=4.286 mm，外筒壁厚在低水平时各响应的平均值为Bl=7.799 mm，外筒壁厚的主效应为Bm=Bh-Bl=-3.513 mm。

内外筒间距在高水平时各响应的平均值为Ch=6.504 mm，内外筒间距在低水平时各响应的平均值为Cl=5.556 mm，内外筒间距的主效应为Cm=Ch-Cl=0.948 mm。

内筒壁厚在高水平时各响应的平均值为Dh=5.220 mm，内筒壁厚在低水平时各响应的平均值为Dl=6.844 mm，内筒壁厚的主效应为Dm=Dh-Dl=-1.624 mm。

加强筋数量在高水平时各响应的平均值为Eh=5.585 mm，加强筋数量在低水平时各响应的平均值为El=6.445 mm，加强筋数量的主效应为Em=Eh-El=-0.86 mm。

加强筋壁厚在高水平时各响应的平均值为Fh=5.844 mm，加强筋壁厚在低水平时各响应的平均值为Fl=6.216 mm，加强筋壁厚的主效应为Fm=Fh-Fl=-0.372 mm。

通过上述分析可以看出，外筒壁厚的主效应对响应的影响最大，加强筋壁厚的主效应对响应的影响最小，各因子的主效应如图2所示。

图2 各因子主效应图

4.1.2 交互效应

外筒直径与外筒壁厚的交互效应为Am×Bm=9.422 ；外筒直径与内外筒间距的交互效应为Am×Cm=-2.492；外筒直径与内筒壁厚的交互效应为Am×Dm=4.268；外筒直径与加强筋数量的交互效应为Am×Em=2.260；外筒直径与加强筋壁厚的交互效应为Am×Fm=0.978；外筒壁厚与内外筒间距的交互效应为Bm×Cm=-3.330；外筒壁厚与内筒壁厚的交互效应为Bm×Dm=5.705；外筒壁厚与加强筋数量的交互效应为Bm×Em=3.021；外筒壁厚与加强筋壁厚的交互效应为Bm×Fm=1.307；内外筒间距与内筒壁厚的交互效应为Cm×Dm=-1.540；内外筒间距与加强筋数量的交互效应为Cm×Em=-0.815；内外筒间距与加强筋壁厚的交互效应为Cm×Fm=-0.3527；内筒壁厚与加强筋数量的交互效应为Dm×Em=1.397；内筒壁厚与加强筋数量的交互效应为Dm×Fm=0.604；加强筋数量与加强筋壁厚的交互效应为Em×Fm=0.32。

通过上述分析可以看出，外筒壁厚与外筒壁厚的交互效应对响应的影响最大，加强筋数量与加强筋壁厚的交互效应对响应的影响最小，各因子之间的交互效应如图3所示。

4.2 优化

图3 各因子之间的交互效应图

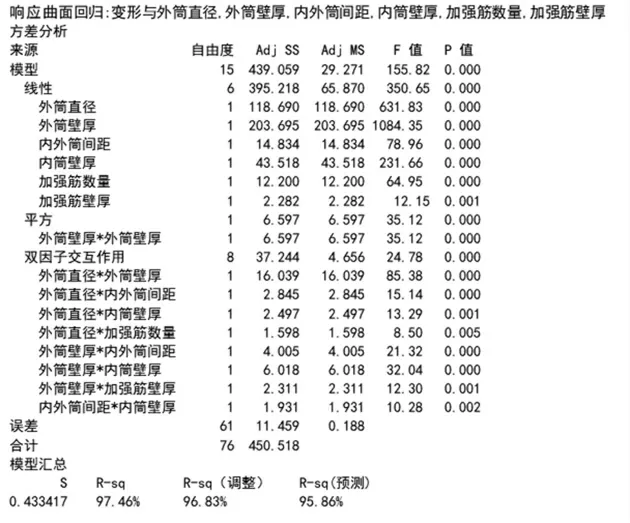
图4 变形量优化

利用Minitab软件针对仿真结果进行分析，响应为变形量的优化，如图4所示，从中可以看出，变形量和外筒直径、外筒壁厚、内外筒间距、内筒壁厚、加强筋数量、加强筋壁厚强相关（P值<0.05），和外筒壁厚的平方强相关（P值<0.05），和外筒直径与外筒壁厚、外筒直径与内外筒间距、外筒直径与内筒壁厚、外筒直径与加强筋数量、外筒壁厚与内外筒间距、外筒壁厚与内筒壁厚、外筒壁厚与加强筋数量、内外筒间距与内筒壁厚交互作用强相关（P值<0.05）。

经过上述优化得到变形量的传递函数为y=53.95-0.009196A -0.8468B +0.01812C -0.3174D-0.414E-0.0409F +0.003718B2+0.000111AB -0.00004AC +0.000044AD+0.000088AE-0.000083BC+0.001363BD+0.000845BF+0.000058CD-0.000033CF+0.000439DF。

利用Minitab软件针对仿真结果进行分析，响应为应力的优化，如图5所示，从中可以看出，变形量和外筒直径、外筒壁厚、内外筒间距、内筒壁厚、加强筋数量、加强筋壁厚强相关（P值<0.05），和外筒壁厚的平方强相关（P值<0.05），和外筒直径与外筒壁厚、外筒壁厚与内外筒间距、内外筒间距与内筒壁厚交互作用强相关（P值<0.05）。

经过上述优化得到应力的传递函数为y=119.2-0.01698A-2.369B+0.01606C-0.2362D-0.1176E-0.0402F+0.01756B2+0.000243AB-0.0005BC+0.000256CD。

悬臂支架对变形量的要求更严，对应力的要求是不产生破坏、不产生永久的变形即可，因此针对变形量使用响应优化器进行优化，变形量为5 mm，参数优化如图6所示，再将产生的各参数代入到应力的传递函数中进行验证，不超过许用应力即可。

图5 应力优化

图6 参数优化图

针对变形量进行优化从而得到各参数的最佳参数，外筒直径为3900 mm，外筒壁厚为35 mm，内外筒间距为500 mm，内筒壁厚为35 mm，加强筋数量为12根，加强筋壁厚为50 mm,变形量为5.07 mm。将这些参数代入到应力的传递函数中，得到应力的最大数值为16.815 MPa，小于所用材料Q345的许用应力230 MPa，满足强度要求。