基于推广的Fu-Shu坏单元指示子的h自适应RKDG方法

韩文秀, 王海云, 朱洪强

(南京邮电大学理学院, 南京 210023)

求解双曲守恒律方程的Runge-Kutta间断Galerkin方法(the Runge-Kutta discontinuous Galerkin method, RKDG)[1]具有精度高、易于处理复杂计算区域和边界条件、求解高效、并行效率高、易于进行hp自适应等优点, 它已成为当今科学计算领域高分辨方法的研究前沿和热点,也是计算流体力学的主流方法之一．非线性双曲守恒律方程的解经常含有间断,如果使用固定网格来求解,为了提高间断的求解效果,只能在全部计算区域上使用密网格,从而导致计算量大幅增加．自适应方法是解决这个问题的一种有效策略,它能根据解的情况按一定要求以自适应的方式重新生成网格,从而节约计算成本．h自适应RKDG方法目前已有不少研究工作, 如Remacle[2]、Hartmann[3]和Dedner[4]等人分别基于误差估计生成自适应网格．另一种h自适应策略基于所谓的坏单元指示子, 包括Devine[5]、Zhu[6-7]等人的研究工作, 这种方法因为不需要使用较难得到的误差估计而相对简单, 同时也能实现良好的自适应效果,故近些年仍不断出现新的研究成果[8-11]．

RKDG方法需要限制器[1]来控制间断附近的数值伪振荡, 以保持格式稳定．坏单元指可能含有间断,需要限制器发挥作用的单元,而坏单元指示子通常来自各种限制器或激波探测技术．Zhu等[6]利用坏单元指示子将每个单元标记为坏单元或好单元,采用加密坏单元、合并好单元的策略,实现了在间断区域使用密网格、连续区域使用粗网格的自适应效果,有效提高了数值解的质量．区别于普通无悬点的网格,基于单元加密和合并的二维h自适应网格将不可避免地出现悬点,而且不同单元可能会有不同数量和大小的直接邻居单元, 这种几何复杂性导致绝大多数坏单元指示子无法直接用于h自适应网格．常用的KXRCF坏单元指示子[12]是少数能直接应用的指示子, 但文献[6]中的数值结果表明,随着逼近空间次数的增加, KXRCF指示子倾向于标记越来越多的坏单元,导致连续区域也会使用密网格,显著影响自适应的效果．Fu等[13]提出1个新的坏单元指示子,该指示子做法简单,模板紧凑,不含有依赖于问题的敏感参数且数值表现良好; Zhu等[14]将它推广到二维h自适应网格,同时保持了原来的优点．本文拟将这个推广的Fu-Shu坏单元指示子用于h自适应RKDG方法, 从而进一步提高数值解的质量,节约计算成本．

1 二维RKDG方法及h自适应方法

RKDG方法对时间使用非线性稳定的显式RK方法离散, 对空间使用DG离散, 采用分片多项式空间作为近似解和测试函数空间．考虑二维标量双曲守恒律方程

(1)

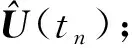
该方法中限制器的坏单元指示子采用推广的Fu-Shu坏单元指示子, 限制器的数值解重构采用WENO重构方法[6]．

2 推广的Fu-Shu坏单元指示子

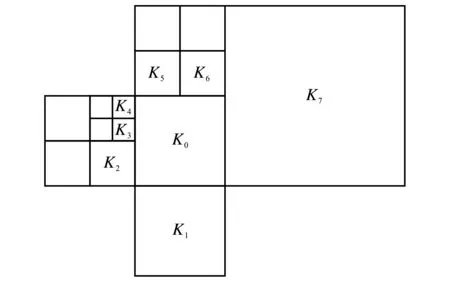
图1 目标单元K0有7个直接邻居单元的示例图Fig.1 An example of the target cell K0 with 7 immediate neighbors

3 数值结果

为了研究推广的Fu-Shu坏单元指示子用于生成h自适应网格, 本文对二维可压Euler方程组

(2)

进行广泛的数值试验, 其中ρ表示密度,u和v分别为x方向和y方向的速度,E是总能量,p是压力, 满足p=(γ-1)[E-0.5ρ(u2+v2)], 式中γ=1.4．文献[6]中使用KXRCF坏单元指示子生成h自适应网格, 在k=1时得到了质量较高的网格, 但在k=2时因为坏单元判断过多导致加密太多,自适应效果仍有改进的空间．在本文的数值试验中,k=1时推广的Fu-Shu坏单元指示子得到了与KXRCF指示子效果相当的自适应网格, 故下面仅讨论k=2时的数值解和自适应网格图,以展示推广的Fu-Shu指示子在高阶时的优势．在所有的数值试验中均取Lmax=4．

例1黎曼问题．求解带有以下初值条件的方程(2):

图2给出了初始单元尺寸Δx0=Δy0=1/80,t=0.25时的密度等高线图和网格图．从图2中可以看出, 推广的Fu-Shu坏单元指示子精准捕捉到了间断, 并在间断区域使用了最密网格,而其他区域使用了粗网格, 达到了预期的自适应效果．对比文献[6]图6中k=2时的密度等高线图和网格图, 推广的Fu-Shu指示子得到的结果在间断处的加密区域更窄, 也没有连续区域被误加密的问题．

图2 黎曼问题在t=0.25时的密度等高线图(a)和网格图(b)Fig.2 Density contours (a) and mesh (b) at t=0.25 for the Riemann problem

例2双马赫反射问题．取计算区域[0,4]×[0,1], 底边1/6≤x≤4区域为固壁, 初始时与底边交于(1/6,0)并与底边成60°夹角的激波以10马赫的速度撞击固壁．波前未受干扰的空气密度为1.4, 压力为1．底边0≤x≤1/6区域使用精确波后边界条件, 其余区域使用反射边界条件．顶部的边界条件使用描述10马赫激波的精确边界条件, 左右边界分别使用入流和出流边界条件．图3给出了Δx0=Δy0=1/60,t=0.2时的密度等高线图和网格图．图3显示,最终网格和间断线相吻合, 自适应方法在光滑区域生成了初始粗网格,而在间断附近生成了充分加密的网格, 自适应效果良好．对比文献[6]图9中k=2时的密度等高线图和网格图, 推广的Fu-Shu坏单元指示子只在必要的间断附近加密网格, 被加密区域小很多, 相应的计算成本也更低．

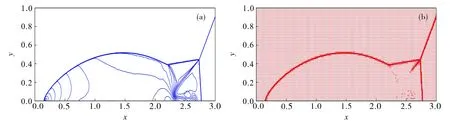
图3 双马赫反射问题在t=0.2时的密度等高线图(a)和网格图(b)Fig.3 Density contours (a) and mesh (b) at t=0.2 for the double Mach reflection problem

例3前台阶问题．问题始于长度为3, 高度为1的风洞中, 风洞底部的台阶高0.2,位于距离风洞左侧0.6处并一直延伸到风洞右端．初始时, 速度为3马赫的均匀空气向右流动,空气密度为1.4,压力为1．风洞壁和台阶处为反射边界,左右边界分别为入流和出流边界．台阶角为奇点,采用与文献[13]同样的方法处理．图4给出了Δx0=Δy0=1/40,t=4.0时的密度等高线图和网格图．从图4中的结果以及对比文献[6]图7中k=2时的结果可知, 推广的Fu-Shu坏单元指示子捕捉间断更加精准, 并生成了质量更高的自适应网格．

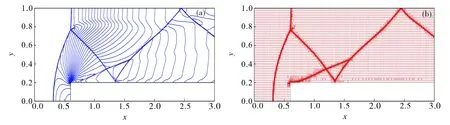
图4 前台阶问题在t=4.0时的密度等高线图(a)和网格图(b)Fig.4 Density contours (a) and mesh (b) at t=4.0 for the forward-facing step problem

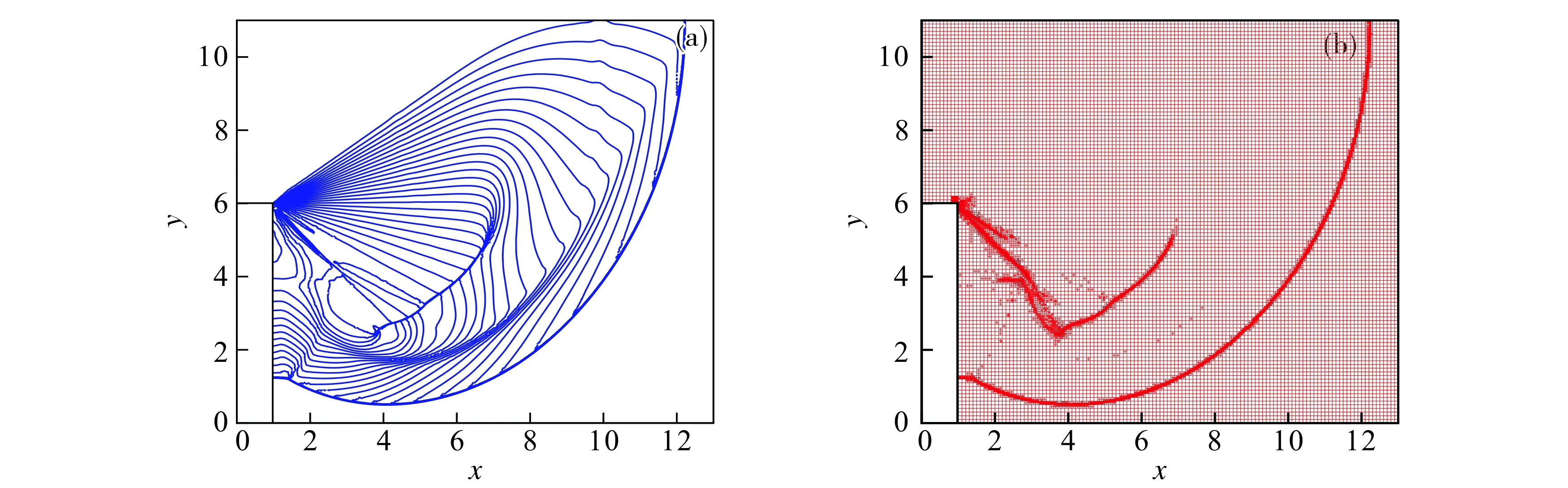
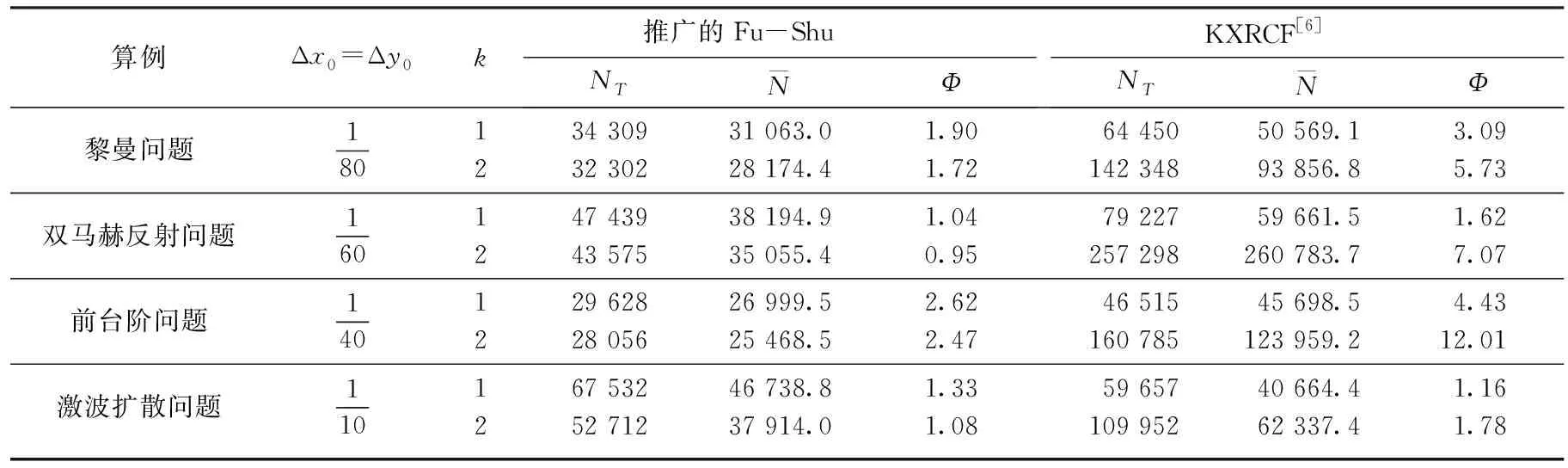
例4激波扩散问题．计算域为[0,1]×[6,11]∪[1,13]×[0,11]．激波初始时位于x=0.5, 6

图5 激波扩散问题在t=2.3时的密度等高线图(a)和网格图(b)Fig.5 Density contours (a) and mesh (b) at t=2.3 for the shock diffraction problem

表1 自适应网格数据表