带参数时空分数阶Fokas-Lenells 方程的精确解*

刘杨秀， 胡彦霞

（华北电力大学 数理学院，北京 102206）

引 言

近几十年来，分数阶非线性偏微分方程的研究已渗透到许多科学领域中.由整数阶微分方程推广出的分数阶微分方程，在描述一些系统的动力学行为中，更加能反映出系统的实际变化规律[1].众所周知的分数阶非线性Schrödinger 方程就是非常典型的一类非线性发展方程.很多分数阶非线性偏微分方程与深水波动、潜水波动现象有着紧密的联系.如果知道这类方程的精确解，将有利于数值模拟进行检验以及定性分析.由此我们需要了解分数阶导数各种详细的定义，比如R-L 分数阶导数、Caputo 分数阶导数等[2-4]，同样用来解决整数阶非线性偏微分方程的方法，也可以应用到分数阶非线性偏微分方程上.从现有文献看，求解分数阶非线性偏微分方程的方法已有众多，比如试探函数法[5]、Horita 法[6]、扩展的直接代数法[7]、李群方法[8-9]、Jacobi 椭圆函数法[10]、扩展的Jacobi 椭圆函数法[11]、广义G′/G方法[12]、sine-Gordon 方法[13]、多项式完全判别系统法[14]以及其他求解方法[15-24].由于非线性分数阶偏微分方程的多样性及复杂性和每一种求解方法的局限性，还未能有一种通用的普遍有效的求解方法.因此，运用有效的方法去求非线性分数阶偏微分方程的精确解仍是一个需要不断研究的课题之一.随着MATLAB 等其他数学软件的应用和普及，借助计算机软件可以帮助我们更方便地解决这一问题.

本文主要考虑非线性光学领域中的带参数时空分数阶Fokas-Lenells 方程[25]：

多项式完全判别系统法是一种求解此类问题比较有效的方法，是将偏微分方程在行波变换下简化为常微分方程，再对常微分方程中的多项式进行完整分类并求解相应积分，从而得到原方程的精确解.对于分数阶偏微分方程，若其在行波变换下简化为u′(ξ)=G(u,θ1,θ2,···,θm)(θ1,θ2,···,θm为 相应参数，且G(u,θ1,θ2,···,θm)是关于u的多项式)的形式，就可以利用此方法进行求解.关于此方法的介绍及应用详见文献[37-41].

本文考虑方程(1)在一般情况下的解的问题，利用多项式完全判别系统法，根据对方程(1)单行波解的完整分类，在不做任何参数限制的条件下，求得方程(1)在一般情况下的9 种精确解，包括有理函数解、周期解、孤波解、Jacobi 椭圆函数解和双曲函数解等，绘制了精确解的相关图像，由此分析了参数对解的结构的影响.

1 预 备 知 识

2 带参数时空分数阶Fokas-Lenells 方程的约化分析

首先对方程进行行波变换，令

3 带参数Fokas-Lenells 方程的精确解

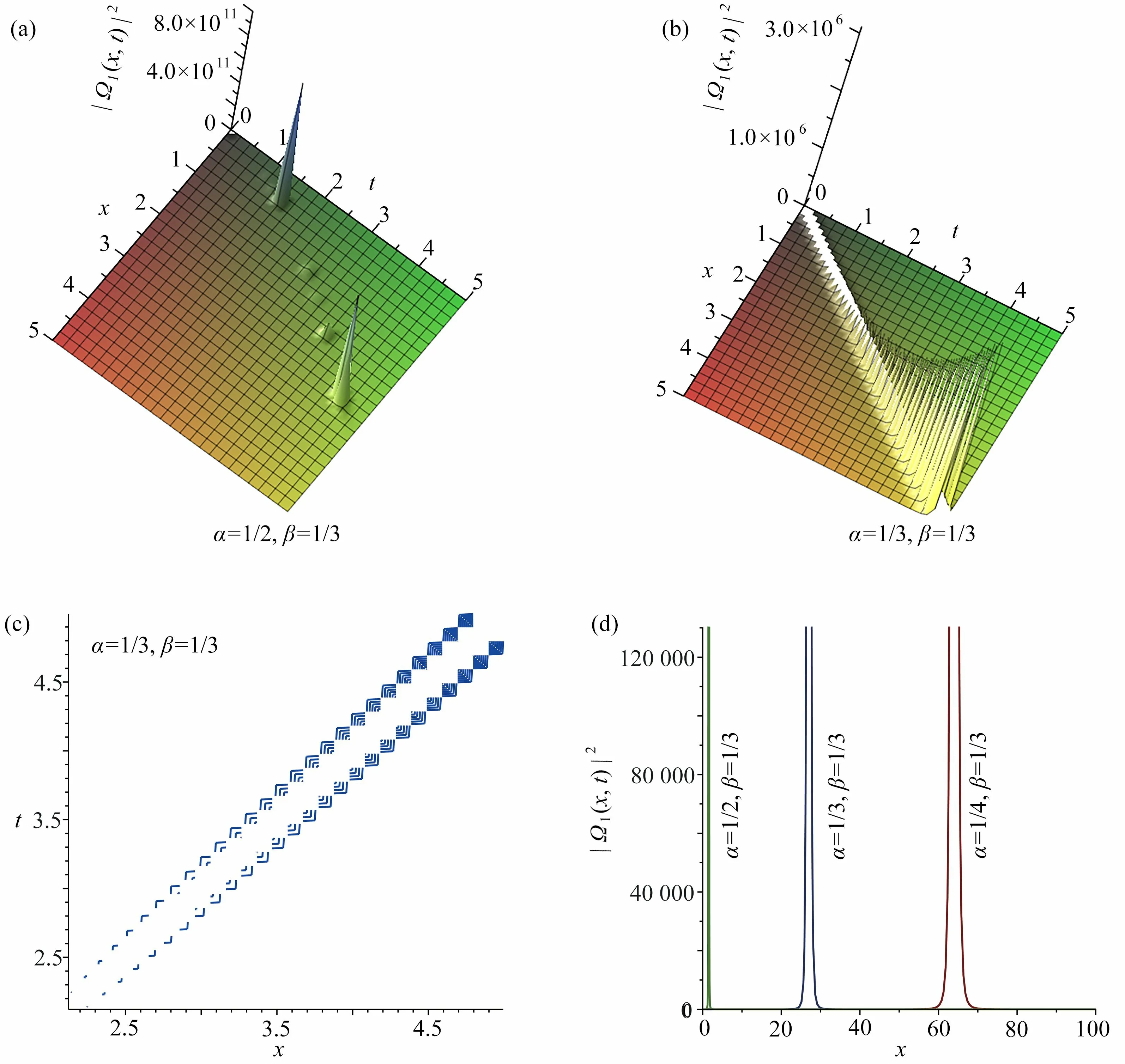
图1 | Ω1(x,t)|2取 不同分数阶导数值时的三维图，图1(b)对应的等高线图，以及t =3 时| Ω1(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω1(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω1(x,t)|2 的 三维图； (c) 图1(b)的等高线图； (d) 当t =3 时| Ω1(x,t)|2关 于x 的截面图Fig. 1 The 3D graph of | Ω1(x,t)|2 with different values of the fractional derivative, the contour plot of fig.1(b) and the sectional view of | Ω1(x,t)|2 against x with t =3: (a) the graphic model of | Ω1(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω1(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig.1(b);(d) the sectional view of | Ω1(x,t)|2 against x when t=3

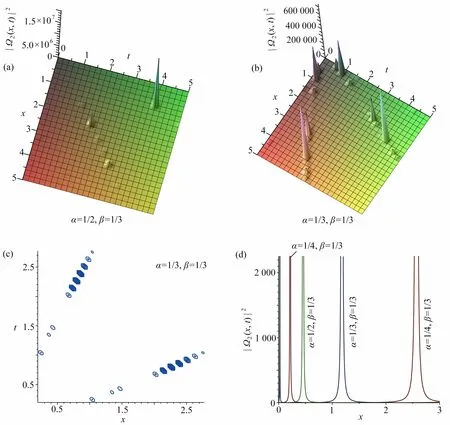
图2 | Ω2(x,t)|2取 不同分数阶导数值时的三维图，图2(b)对应的等高线图，以及t =3 时| Ω2(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω2(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω2(x,t)|2 的 三维图； (c) 图2(b)的等高线图； (d) 当t =3 时| Ω2(x,t)|2关 于x 的截面图Fig. 2 The 3D graph of | Ω2(x,t)|2 with different values of the fractional derivative, the contour plot of fig.2(b) and the sectional view of | Ω2(x,t)|2 against x with t =3: (a) the graphic model of | Ω2(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω2(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig.2(b);(d) the sectional view of | Ω2(x,t)|2 against x when t=3

经检验，此情况不成立，不予讨论.

图3 | Ω3(x,t)|2取 不同分数阶导数值时的三维图，图3(b)对应的等高线图，以及t =3 时| Ω3(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω3(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω3(x,t)|2 的 三维图； (c) 图3(b)的等高线图； (d) 当t =3 时| Ω3(x,t)|2关 于x 的截面图Fig. 3 The 3D graph of | Ω3(x,t)|2 with different values of the fractional derivative, the contour map of fig. 3(b) and the sectional view of | Ω3(x,t)|2 against x with t =3: (a) the graphic model of | Ω3(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω3(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig. 3(b);(d) the sectional view of | Ω3(x,t)|2 against x when t=3

图4 | Ω4(x,t)|2取 不同分数阶导数值时的三维图，图4(b)对应的等高线图，以及t =3 时| Ω4(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω4(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω4(x,t)|2 的 三维图； (c) 图4(b)的等高线图； (d) 当t =3 时| Ω4(x,t)|2关 于x 的截面图Fig. 4 The 3D graph of | Ω4(x,t)|2 with different values of the fractional derivative, the contour plot of fig.4(b) and the sectional view of | Ω4(x,t)|2 against x with t =3: (a) the graphic model of | Ω4(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω4(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig.4(b);(d) the sectional view of | Ω4(x,t)|2 against x when t=3

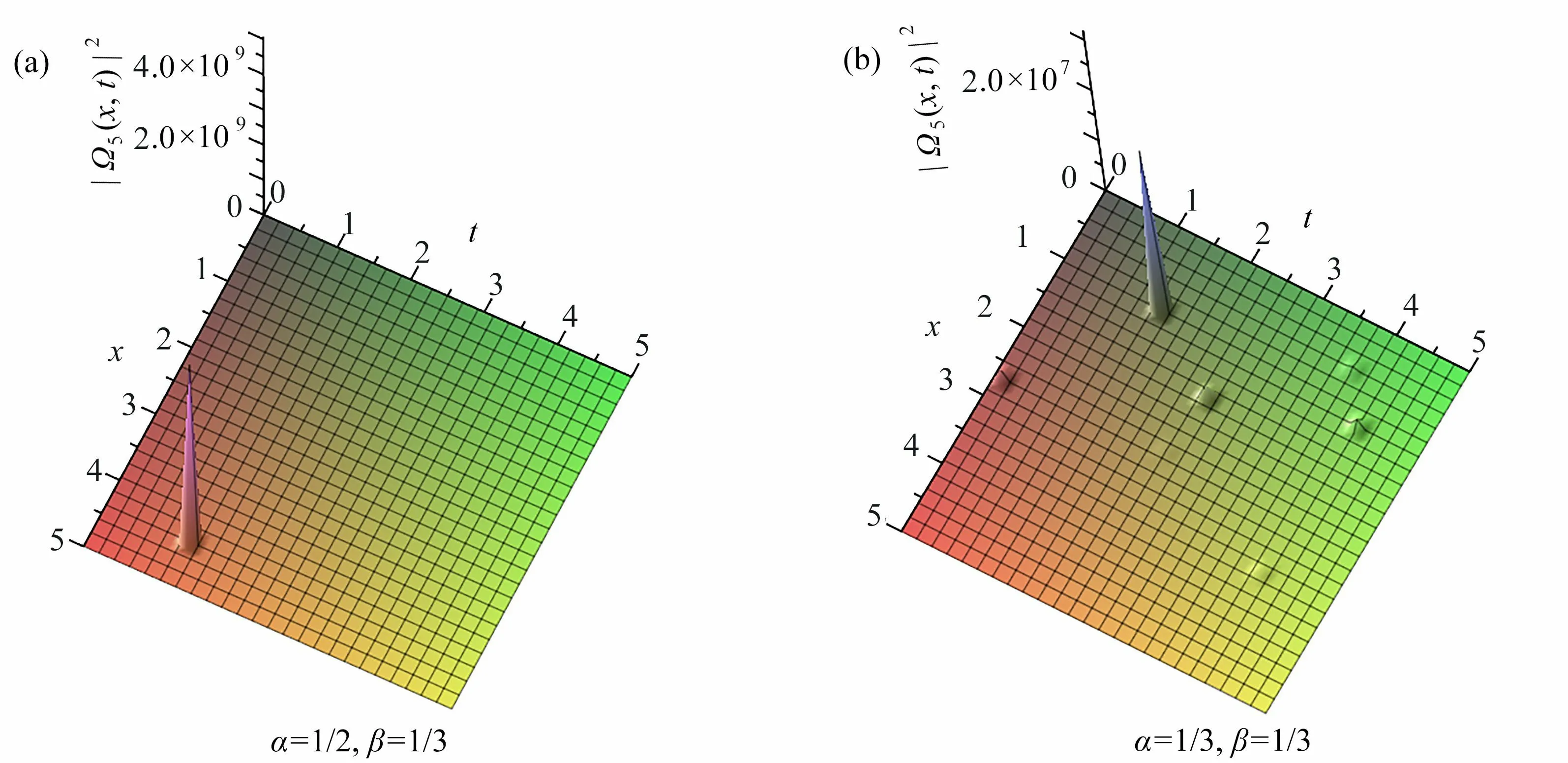
图5 | Ω5(x,t)|2取 不同分数阶导数值时的三维图，图5(b)对应的等高线图，以及t =3 时| Ω5(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω5(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω5(x,t)|2 的 三维图； (c) 图5(b)的等高线图； (d) 当t =3 时| Ω5(x,t)|2关 于x 的截面图Fig. 5 The 3D graph of | Ω5(x,t)|2 with different values of the fractional derivative, the contour plot of fig. 5(b) and the sectional view of | Ω5(x,t)|2 against x with t =3: (a) the graphic model of | Ω5(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω5(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig. 5(b);(d) the sectional view of | Ω5(x,t)|2 against x when t=3

图6 | Ω6(x,t)|2取 不同分数阶导数值时的三维图，图6(b)对应的等高线图，以及t =3 时| Ω6(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω6(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω6(x,t)|2 的 三维图； (c) 图6(b)的等高线图；(d) 当t =3 时| Ω6(x,t)|2关 于x 的截面图Fig. 6 The 3D graph of | Ω6(x,t)|2 with different values of the fractional derivative, the contour plot of fig. 6(b) and the sectional view of | Ω6(x,t)|2 against x with t =3: (a) the graphic model of | Ω6(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω6(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig. 6(b);(d) the sectional view of | Ω6(x,t)|2 against x when t=3

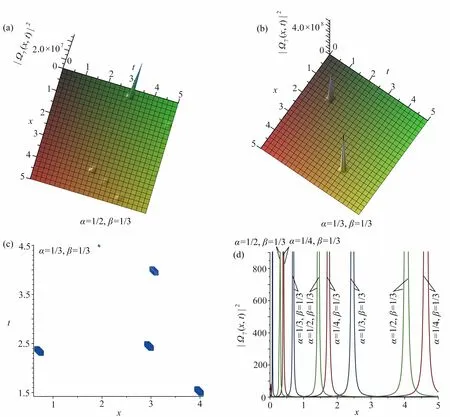
图7 | Ω7(x,t)|2取 不同分数阶导数值时的三维图，图7(b)对应的等高线图，以及t =3 时| Ω7(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω7(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω7(x,t)|2 的 三维图； (c) 图7(b)的等高线图； (d) 当t =3 时| Ω7(x,t)|2关 于x 的截面图Fig. 7 The 3D graph of | Ω7(x,t)|2 with different values of the fractional derivative, the contour plot of fig.7(b) and the sectional view of | Ω7(x,t)|2 against x with t =3: (a) the graphic model of | Ω7(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω7(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig.7(b); (d) the sectional view of | Ω7(x,t)|2 against x when t=3

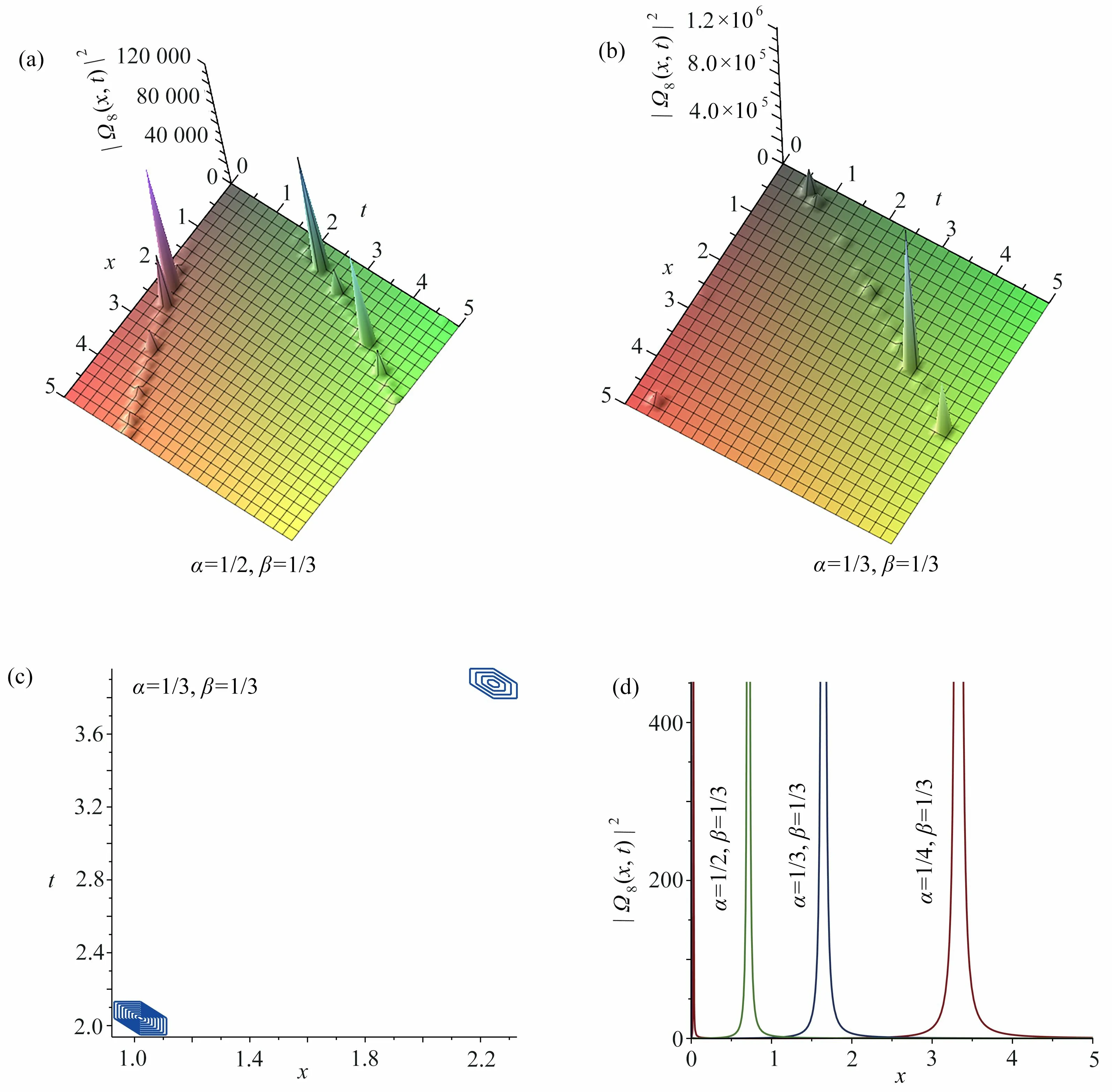
图8 | Ω8(x,t)|2取 不同分数阶导数值时的三维图，图8(b)对应的等高线图，以及t =3 时| Ω8(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω8(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω8(x,t)|2 的 三维图； (c) 图8(b)的等高线图； (d) 当t =3 时α =1/2,β=1/3,|Ω8(x,t)|2 关 于x 的截面图Fig. 8 The 3D graph of | Ω8(x,t)|2 with different values of the fractional derivative, the contour plot of fig. 8(b) and the sectional view of | Ω8(x,t)|2 against x with t =3: (a) the graphic model of | Ω8(x,t)|2,α=1/2,β=1/3; (b) the graphic model of |Ω 8(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig. 8(b);(d) the sectional view of | Ω8(x,t)|2 against x when t=3

图9 | Ω9(x,t)|2取 不同分数阶导数值时的三维图，图9(b)对应的等高线图，以及t =3 时| Ω9(x,t)|2关 于 x 的 截面图：(a) α =1/2,β=1/3,|Ω9(x,t)|2的三维图； (b) α =1/3,β=1/3,|Ω9(x,t)|2 的 三维图； (c) 图9(b)的等高线图； (d) 当t =3 时| Ω9(x,t)|2关 于x 的截面图Fig. 9 The 3D graph of | Ω9(x,t)|2 with different values of the fractional derivative, the contour plot of fig.9(b) and the sectional view of | Ω9(x,t)|2 against x with t =3: (a) the graphic model of | Ω9(x,t)|2,α=1/2,β=1/3; (b) the graphic model of | Ω9(x,t)|2,α=1/3,β=1/3; (c) the contour plot of fig.9(b);(d) the sectional view of | Ω9(x,t)|2 against x when t=3

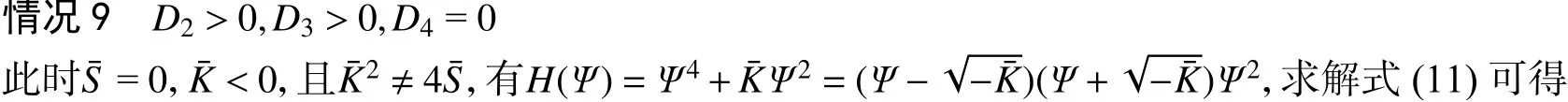
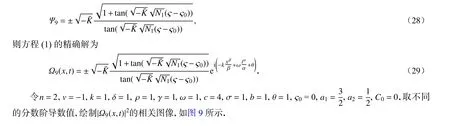
4 结 果 分 析

方程精确解的结构反映了光学系统描述的波在介质中传播的特性.这里，我们主要讨论分析分数阶参数α ， β 的变化对解的结构的影响.根据前面对方程(1)精确解的 |Ωi(x,t)|2的相关图形的分析发现，在图1、3、5、7、9 中，当其中一参数 β不变，参数α 变化时，对应的方程的奇异解的结构没有发生本质的变化，只有波峰会向左或向右偏移，或出现几个零散的波峰.由于这些奇异解在波峰处有一个不连续的一阶导数，这反映出对应的方程(1)描述的波传播的特性.在图2、8 中，当参数α 变化时，奇异周期解的结构及奇异性、周期性也并未发生大的改变.在图4 中，随着 α的减小，扭波峰值会向右移动，但扭波仍然存在，其等高线分布仅在很小的时间范围内波动，但在t=0.1左 右出现新的走势.在图6 中，随着α 的变化，对应的奇异解的结构也没有发生质的变化，但从等高线密集程度来看，有几条明显的“山脉”，反映了此时方程(1)描述的波传播的情况.

5 结 论

本文通过行波变换，将光学系统中带参数时空分数阶Fokas-Lenells 方程转换成常微分方程，然后利用多项式完全判别系统法对该方程进行了单行波解的完整分类，在不对方程中的参数和n做任何限定的情况下，得到了方程在一般情况下的精确解，包括有理函数解、孤立波解、双曲函数解、周期解、Jacobi 椭圆函数解等.在现有文献中，还没有见到对带参数时空分数阶Fokas-Lenells 方程中的参数和n不做任何限定的情况下求的精确解的相关结论.这是本文与其他已有文献不同的地方.为了更好地理解此模型的物理现象和研究光孤子的传播特性，我们绘制了精确解的相关三维图、等高线图及截面图，讨论了分数阶参数对解的影响.随着分数阶导数值的变化，比如 β 不变， α减小时，方程的解的结构并未发生质的变化，这也反映出了此时光脉冲在介质中的传播特性.多项式完全判别系统法不仅可以用来求偏微分方程的精确解，也可以对方程进行定性分析，这也将是我们此后工作的一部分.

参考文献（ References ） ：

［1］W ANG B H, WANG Y Y, DAI C Q, et al. Dynamical characteristic of analytical fractional solitons for the space-time fractional Fokas-Lenells equation[J].Alexandria Engineering Journal, 2020, 59（6）: 4699-4707.

［2］K ILBAS A, SRIVASTAVA H M, TRUJILLO J J.Theory and Applications of Fractional Differential Equations[M]. Amsterdam: Elsevier Science, 2006.

［3］M ILLER K S, ROSS B.An Introduction to the Fractional Calculus and Fractional Differential Equations[M].Wiley-Interscience,1993.

［4］A TANGANA A.Derivative With a New Parameter Theory, Methods and Applications[M]. Amsterdam: Elsevier Science, 2015.

［5］P ANDIR Y, EKIN A. Dynamics of combined soliton solutions of unstable nonlinear Schrödinger equation with new version of the trial equation method[J].Chinese Journal of Physics, 2020, 67: 534-543.

［6］L IU XIAOYAN, ZHOU Q, BISWAS A, et al. The similarities and differences of different plane solitons controlled by (3 + 1)-dimensional coupled variable coefficient system[J].Journal of Advanced Research, 2020, 24:167-173.

［7］S AJID N, AKRAM G. Optical solitons with full nonlinearity for the conformable space-time fractional Fokas-Lenells equation[J].Optik, 2019, 196: 163131.

［8］H ASHEMI M S, BALEANU D.Lie Symmetry Analysis of Fractional Differential Equations[M]. New York:Chapman and Hall/CRC , 2020.

［9］ 胡 彦鑫, 郭增鑫, 辛祥鹏. 一类Burgers-KdV方程的李群分析、李代数、对称约化及精确解[J]. 聊城大学学报(自然科学版), 2021, 34（2）: 8-13. （HU Yanxin, GUO Zengxin, XIN Xiangpeng. Lie group analysis, Lie algebra, symmetric reduction and exact solutions of a class of nonlinear evolution equations[J].Journal of Liaocheng University(Natural Science), 2021, 34（2）: 8-13.（in Chinese））

［10］K ALBANI K, AL-GHAFRI K S, KRISHNAN E V, et al. Pure-cubic optical solitons by Jacobi’s elliptic function approach[J].Optik, 2021, 243: 167404.

［11］B ISWAS A, EKICI M, SONMEZOGLU A, et al. Highly dispersive optical solitons with non-local nonlinearity by extended Jacobi’s elliptic function expansion[J].Optik, 2019, 184: 277-286.

［12］M ANAFIAN J, AGHDAEI M F, JEDDI R S, et al. Application of the generalizedG'/G-expansion method for nonlinear PDEs to obtaining soliton wave solution[J].Optik, 2017, 135: 395-406.

［13］K ALLEL W, ALMUSAWA H, MIRHOSSEINI-ALIZAMINI S M, et al. Optical soliton solutions for the coupled conformable Fokas-Lenells equation with spatio-temporal dispersion[J].Results in Physics, 2021, 26: 104388.

［14］ 胡 艳, 孙峪怀. 应用多项式完全判别系统方法求解时空分数阶复Ginzburg-Landau方程[J]. 应用数学和力学, 2021,42（8）: 874-880. （HU Yan, SUN Yuhuai. Solutions to space-time fractional complex Ginzburg-Landau equations with the complete discrimination system for polynomial method[J].Applied Mathematics and Mechanics, 2021,42（8）: 874-880.（in Chinese））

［15］C AO Q, DAI C. Symmetric and anti-symmetric solitons of the fractional second-and third-order nonlinear Schrödinger equation[J].Chinese Physics Letters, 2021, 38（9）: 090501.

［16］D AI C Q, WANG Y Y, ZHANG J F. Managements of scalar and vector rogue waves in a partially nonlocal nonlinear medium with linear and harmonic potentials[J].Nonlinear Dynamics, 2020, 102: 179-391.

［17］F EI J, CAO W. Explicit soliton-cnoidal wave interaction solutions for the (2 + 1)-dimensional negative-order breaking soliton equation[J].Waves in Random and Complex Media, 2020, 30（1）: 54-64.

［18］H AN H, LI H, DAI C. Wick-type stochastic multi-soliton and soliton molecule solutions in the framework of nonlinear Schrödinger equation[J].Applied Mathematics Letters, 2021, 120: 107302.

［19］A RSHED S, RAZA N. Optical solitons perturbation of Fokas-Lenells equation with full nonlinearity and dual dispersion[J].Chinese Journal of Physics, 2020, 63: 314-324.

［20］Y OUNIS M, SEADAWY A R, BABER M Z, et al. Analytical optical soliton solutions of the Schrödinger-Poisson dynamical system[J].Results in Physics, 2021, 27: 104369.

［21］F ANG Y, WU G Z, WANG Y Y, et al. Data-driven femtosecond optical soliton excitations and parameters discovery of the high-order NLSE using the PINN[J].Nonlinear Dynamics, 2021, 105: 603-616.

［22］R AGHURAMAN P J, BAGHYA SHREE S, MANI RAJAN M S. Soliton control with inhomogeneous dispersion under the influence of tunable external harmonic potential[J].Waves in Random and Complex Media, 2021,31（3）: 474-485.

［23］D AI C Q, WANG Y Y. Coupled spatial periodic waves and solitons in the photovoltaic photorefractive crystals[J].Nonlinear Dynamics, 2020, 102: 1733-1741.

［24］A IN Q T, HE J H, N ANJUM, et al. The fractional complex transform: a novel approach to the time-fractional Schrödinger equation[J].Fractals, 2021, 28（7）: 2150002.

［25］S HEHATA M, REZAZADEH H, ZAHRAN E, et al. New optical soliton solutions of the perturbed Fokas-Lenells equation[J].Communications in Theoretical Physics, 2019, 71（11）: 13-18.

［26］T RIKI H, WAZWAZ A M. Combined optical solitary waves of the Fokas-Lenells equation[J].Waves in Random and Complex Media, 2017, 27（4）: 587-593.

［27］A LI KHALID K, OSMAN M S, ABDEL-ATY M. New optical solitary wave solutions of Fokas-Lenells equation in optical fiber via Sine-Gordon expansion method[J].Alexandria Engineering Journal, 2020, 59（3）: 1191-1196.

［28］B ULUT H, ABDULKADIR SULAIMAN T, MEHMET BASKONUS H, et al. Optical solitons and other solutions to the conformable space-time fractional Fokas-Lenells equation[J].Optik, 2018, 172: 20-27.

［29］T RIKI H, ZHOU Q, LIU W, et al. Localized pulses in optical fibers governed by perturbed Fokas-Lenells equation[J].Physics Letters A, 2022, 421: 127782.

［30］B ISWAS A, YILDIRM Y, YASAR E, et al. Optical soliton solutions to Fokas-Lenells equation using some different methods[J].Optik, 2018, 173: 21-31.

［31］B ISWAS A, EKICI M, SONMEZOGLU A, et al. Optical solitons with differential group delay for coupled Fokas-Lenells equation by extended trial function scheme[J].Optik, 2018, 165: 102-110.

［32］Z HANG Y, YANG J W, CHOW K W, et al. Solitons, breathers and rogue waves for the coupled Fokas-Lenells system via Darboux transformation[J].Nonlinear Analysis:Real World Applications, 2017, 33: 237-252.

［33］Z HANG Q, ZHANG Y, YE R. Exact solutions of nonlocal Fokas-Lenells equation[J].Applied Mathematics Letters, 2019, 98: 336-343.

［34］Y AKUP Y, BISWAS A, DAKOVA A, et al. Cubic-quartic optical soliton perturbation with Fokas-Lenells equation by sine-Gordon equation approach[J].Results in Physics, 2021, 26: 104409.

［35］D IEU DONNE G, TIOFACK C G L, SEADAWY A, et al. Propagation of W-shaped, M-shaped and other exotic optical solitons in the perturbed Fokas-Lenells equation[J].The European Physical Journal Plus, 2020, 135:371.

［36］N ADIA M, GHAZALA A. Exact solitary wave solutions of the (1 + 1)-dimensional Fokas-Lenells equation[J].Optik, 2020, 208: 164459.

［37］ 杨 翠红, 朱思铭, 梁肇军. 多项式代数方程根的完全分类及其应用[J]. 中山大学学报(自然科学版), 2003, 42（1）: 5-8.（YANG Cuihong, ZHU Siming, LIANG Zhaojun. Complete discrimination of the roots of polynomials and its applications[J].Acta Scientiarum Naturalium Universitatis Sunyatseni(Natural Science), 2003, 42（1）: 5-8.（in Chinese））

［38］ 夏 壁灿, 杨路. 多项式判别矩阵的若干性质及其应用[J]. 应用数学学报, 2003, 4: 652-663. （XIA Bican, YANG Lu.Some properties of the discrimination matrix of polynomials with applications[J].Acta Mathematicae Applicatae Sinica, 2003, 4: 652-663.（in Chinese））

［39］ 杨 路, 张景中, 侯晓荣. 非线性代数方程组与定理机器证明[M]. 上海: 上海科技教育出版社, 1996. （YANG Lu,ZHANG Jingzhong, HOU Xiaorong.Machine Proof of Systems of Nonlinear Algebraic Equations and Theorems[M]. Shanghai: Shanghai Science and Technology Education Press, 1996. （in Chinese））

［40］L IU C. Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations[J].Computer Physics Communications, 2009, 181（2）: 317-324.

［41］ 辛 华. 带有微扰项的Fokas-Lenells方程的包络行波模式[J]. 数学的实践与认识, 2021, 51（11）: 324-328. （XIN Hua.The patterns of envelope traveling waves of Fokas-Lenells equation with perturbation term[J].Mathematics inPractice and Theory, 2021, 51（11）: 324-328.（in Chinese））

［42］K HALIL R, HORANI A, YOUSEF A, et al. A new definition of fractional derivative[J].Journal of Computational and Applied Mathematics, 2014, 264: 65-70.

［43］L IU C. Counterexamples on Jumarie’s two basic fractional calculus formulae[J].Communications in Nonlinear Science and Numerical Simulation, 2015, 22（1/3）: 92-94.

［44］L IU C. Counterexamples on Jumarie’s three basic fractional calculus formulae for non-differentiable continuous functions[J].Chaos,Solitons and Fractals, 2018, 109: 219-222.

［45］T ARASOV V E. No nonlocality, no fractional derivative[J].Communications in Nonlinear Science and Numerical Simulation, 2018, 62: 157-163.

［46］T ARASOV V E. No violation of the Leibniz rule, no fractional derivative[J].Communications in Nonlinear Science and Numerical Simulation, 2013, 18（11）: 2945-2948.

［47］W ANG B H, WANG Y Y. Fractional white noise functional soliton solutions of a wick-type stochastic fractional NLSE[J].Applied Mathematics Letters, 2020, 110: 106583.

［48］Y U L J, WU G Z, WANG Y Y, et al. Traveling wave solutions constructed by Mittag-Leffler function of a (2 +1)-dimensional space-time fractional NLS equation[J].Results in Physics, 2020, 17: 103156.

［49］W ANG B H, LU P H, DAI C Q, et al. Vector optical soliton and periodic solutions of a coupled fractional nonlinear Schrödinger equation[J].Results in Physics, 2020, 17: 103036.

［50］D AI C Q, WU G, LI H J, et al. Wick-type stochastic fractional solitons supported by quadratic-cubic nonlinearity[J].Fractals, 2021, 29（7）: 2150192.