改进DCA算法用于工程时序数据异常检测

2020-09-07孙向阳邸泽雷坤

四川职业技术学院学报 2020年4期

徐伟，孙向阳，邸泽雷坤

（上海大学悉尼工商学院，上海 201899）

0 引言

随着我国经济建设的飞速发展，隧道工程建设取得了巨大的成果，然而隧道工程施工具有隐蔽性、复杂性和不确定性等特点，大型隧道工程建设期间都会存在大量的风险，造成隧道施工安全事故频繁发生。随着隧道监测技术的发展，最有效的降低隧道风险的措施就是对隧道施工过程进行实时安全监测，从大量的监测数据中及时、准确地发现异常序列，分析灾害演化规律、建立灾变预警模型。

近年来，很多学者提出了时序数据异常检测技术。Knorr和Ng指出数据集中至少有K个对象与O点的距离大于σ，点O即为异常点。孟凡荣等人提出任意分布的连续时间序列Top-K异常检测方法，在含噪声时序数据对异常结果进行排序,克服噪声对序列异常检测准确性的影响。基于距离的异常检测算法存在较高的计算复杂度，难以确定距离参数等困难。随着人工智能的迅速发展，学者运用新的智能算法解决实际问题，例如K最近邻算法[1]、神经网络[2]、支持向量机[3]。傅娆等[4]利用支持向量机对入侵特征进行分类,将线性不可分问题转化为线性优化问题,寻找最优分类面并进行判断,实现入侵检测的功能。绝大数机器学习算法要求对原始数据进行分析，需要承担巨大的时间成本。本文提出基于信息熵的改进DCA算法，并运用该算法实现对时序数据的异常检测，提高良好的检测效果。

1 DCA算法

1.1 DCA算法概述

树突状细胞进行抗原收集,对抗原数据进行分析处理,最终提呈给树突状细胞(DC),并根据抗原环境值来刺激或抑制T细胞对抗原进行免疫响应。在免疫过程中，细胞存在三种状态：未成熟状态,半成熟状态,成熟状态。未成熟DC能够收集抗原碎片，并感知从组织发出的多种信号,信号包括病原相关分子模式(PAMP),危险信号 (DS),安全信号(SS),发炎信号(IC)。只有PAMP,DS,SS三种信号共同参与下，IC充当信号放大的角色。DC除了收集PAMP,DS,SS信号，自身也会输出三种信号：协同刺激分子(CSM)、半成熟细胞分泌的分子 (semi mature)、成熟细胞分泌的分子(mature)。一旦CSM达到一定浓度，DC根据 semi mature和mature的相对浓度进行分化，未成熟DC转换成半成熟DC或成熟DC，从组织迁移到淋巴结，将抗原提呈给T细胞，促进和抑制免疫反应。成熟DC产生激活因子，刺激T细胞进行免疫应答。半成熟DC产生耐受因子，促使T细胞进行免疫耐受，如图1所示。

图1 DC细胞状态的转化工程

1.2 DCA算法对输入信号的处理

DCA算法的核心就是DC细胞从抗原中提取输入信号，经过权值计算得出输出信号，利用输出信号得到成熟环境抗原值(MCAV),最终对抗原进行评价。

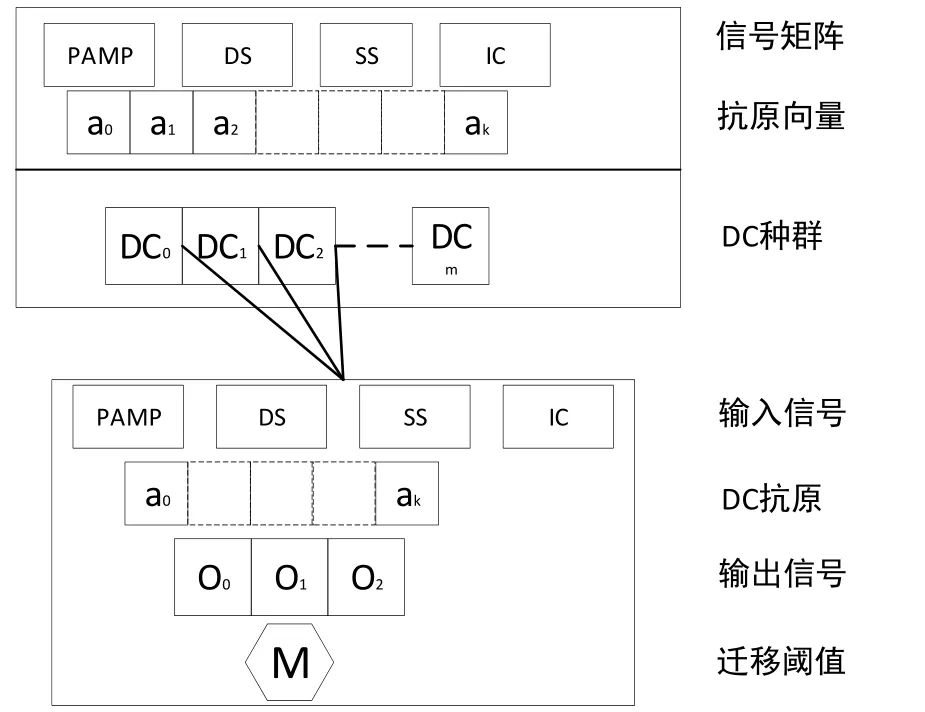
图2 DCA算法中的数据结构

图2 描述了DCA算法的数据结构，每个DC细胞将采取信号融合的机制通过对输入信号进行计算来获取输出信号。输出信号计算公式如下：

在公式(1)中,Oj(j=0,1,2)表示输出信号,O0～O2依次表示 csm、semi mature、mature。Si表示输入信号，S0～S2依次代表 PAMP，DS，SS,Wij表示从Si到Oj的权重值。权值是免疫学者在长期实验过程中总结的经验值,权值正负代表了信号的作用效果，权值的大小代表了输入信号对输出信号的影响程度。常用的权值矩阵如表1所示。

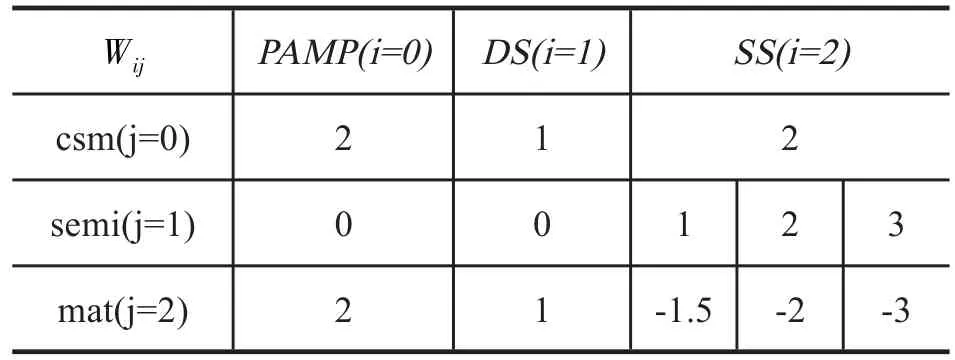
表1 DCA权值矩阵表

1.3 DCA算法步骤

DCA算法对抗原与信号的数据流进行一定的处理,最终输出成熟抗原上下文值。算法经历三个阶段：DC细胞和抗原池初始化阶段、输出信号更新阶段、抗原综合评价阶段。

算法1 DCA算法

输入：PAMP、DS、SS信号。

输出：csm、semi、mat信号、MCAV值。

a)初始化DC种群，确保DC细胞为未成熟状态

b)随机选取DC对信号与抗原进行采样

c)计算输出信号csm,semi,mature并累加求得Σcsm,Σsemi,Σmature。

d)如果Σcsm〉MT(迁移阈值)，相应的DC发生状态迁移，未成熟DC转为成熟DC。

e)判断是否存在待测的信号与抗原。如果仍存在待处理数据，则转到步骤b)。否则转到步骤f)。

f)分别统计每个抗原被成熟DC标记为异常的次数O1以及被未成熟DC标记为正常的次数O2。计算该抗原的MCAV，计算MCAV的公式如下：

从公式(2)可以看出，MCAV的值介于0~1之间，其值用来度量抗原异常的可能性。MCAV越接近于1，则说明该抗原为异常数据的可能性越大；MCAV越接近于0，则说明该抗原为正常数据的可能性越大。

根据算法1的描述，编写描述DC的状态转换和计算MCAV的伪代码。

算法2 描述DC的状态转换

输入：PAMP、DS、SS信号。

输出：csm、semi、mat信号、cell context。

1.initialize DC

2.while Σcsm〈Migration Threshold do

3.get antigen；

4.store antigen；

5.get signals；

6.calculate interim output signals；

7.update cumulative output signals；

8.end

9.if Σsemi〉Σmat then

10.cell context is assigned as 0；

11.else

12.cell context is assigned as 1；

13.end

14.kill cell；

15.replace cell in population；

算法3 计算MCAV值。

输入：抗原上下文值(antigen context)

输出：MCAV。

1.for all antigen in total list do

2.increment antigen count for this antigen type；

3.if antigen context equals 1 then

4.increment antigen type mature count；

5.end

6.end

7.for all antigen types do

8.MCAV of antigen type=mature count/antigen count；

9.end

2 EDCA算法

针对时序数据的异常检测，本文提出了一种基于信息熵理论的改进DCA算法(EDCA)，EDCA算法能够有效地发现时序数据中的异常值。

2.1 时间序列分割算法

本文将时序数据分割成若干个相对短但不重叠的子序列。一般来讲，正常子序列所表现的特征信息别于异常子序列，同时异常子序列带来的局部波动可能会影响前后正常子序列。因此可以将每个子序列看成一个个独立的抗原。DCA是基于DC群体的算法，每个DCA对一个个独立的抗原进行采样(如图3所示)。

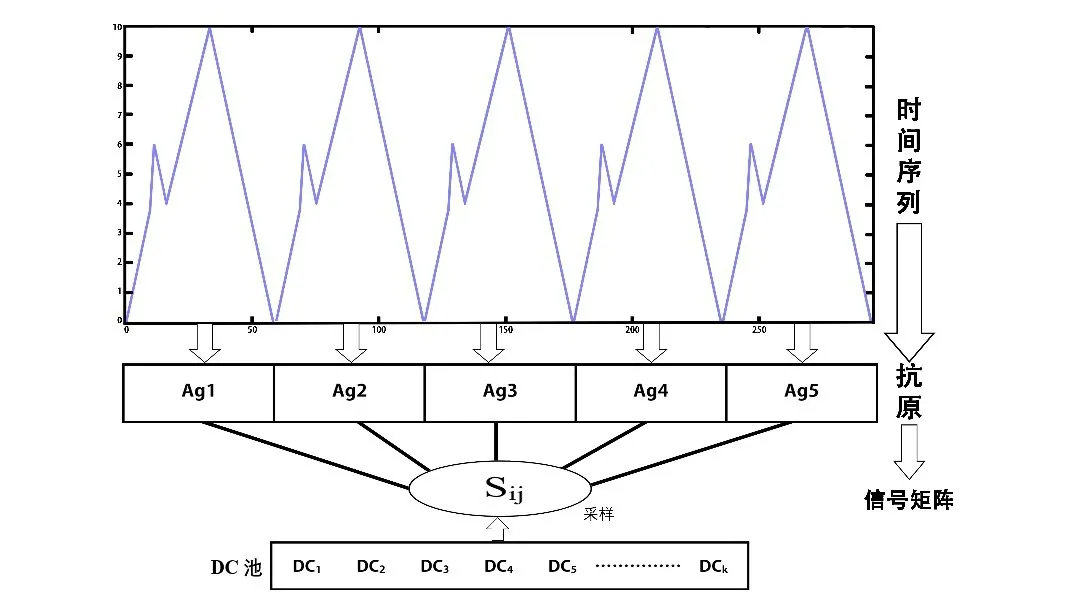
图3 时间序列免疫过程

本文提出基于信息熵的时间序列分割算法(SABE)。通过应用SABE算法对时序数据进行分割，将分割后的子序列模拟成若干个独立的抗原，DC细胞从抗原信号提取PAMP，DS，SS信号，应用EDCA算法对时序数据进行异常检测，EDCA算法流程图如图4所示。

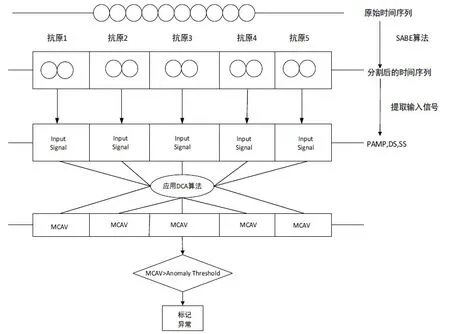
图4 EDCA算法流程图

定义1：信息熵是指某一事件发生时包含的信息量的数学期望，是衡量一个随机变量取值的不确定性程度。系统的随机性越大，非常混乱时信息熵一定很大，反之亦然。信息熵的公式定义如下：

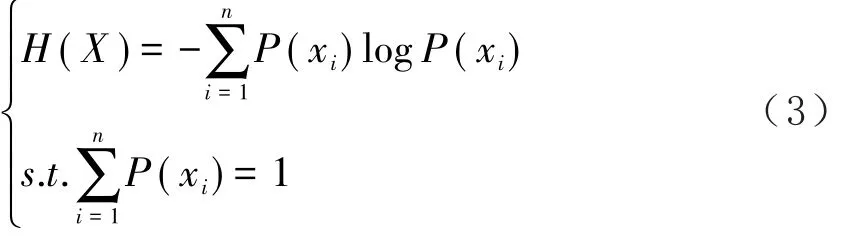
在公式(3)中，P(xi)为序列中第i个序列点的值与所有序列值得总和之比，H(X)为整个序列点的信息熵。

基于信息熵的时间序列分割算法步骤如下：

算法4基于信息熵的时间序列分割

输入：时序数据。

输出：分割窗口长度。

a)序列点差值符号化：为了计算时间序列的信息熵，需要对每一个序列点进行符号化。在时间序列X=x(ti)中，设P=x(ti+1)-x(ti),Q=x(ti)-x(ti-1)。

如果 P×Q〈0,该点置为 0；如果 P×Q〉0,该点置为1；如果P×Q=0，该点位置2.则时间原序列X=x(ti)就转换成由{0,1,2}组成的符号化序列S。

b)求各个子序列的信息熵：设符号化时间序列S的长度为L，分成k段等宽度的时间序列窗口，则子序列的长度均为L/k。设第i个子序列中“0”的数量和为 Cio、“1”的数量和为 Ci1、“2”的数量和为Ci2,第i个子序列的熵H(Xi)。计算H(Xi)如公式(4)所示。

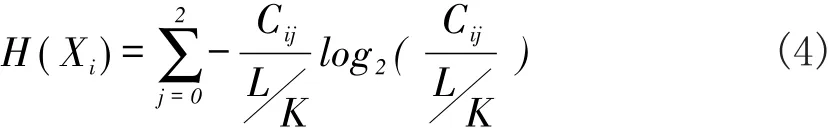
c)确定时间序列分割窗口长度：当子序列的熵极差越大时，选取分割时间序列的窗口长度合适。偏大或偏小的窗口长度均不合适。

算法5 计算最优窗口长度

输入：时序数据。

输出：分割窗口长度。

1.Set the window size as k

2.Take symbolic time series S as input data

3.For k=0.8%×length(S)：3%×length(S)

4.Calculate entropy of every subse-quence with k

5.Set dictionary[k]=range(entropy)

6.End for

7.Get k by sorting dictionary；

8.end

2.2 EDCA算法中输入信号的提取

本文采用方差，平均值，中位数，标准差，极差对每个抗原对应的子序列进行特征提取。根据先验知识，选取极差属性列来计算PAMP和SS信号，其计算过程见算法6。其余四个属性列(方差、平均值、中位数、标准差)用来计算DS信号，其计算过程见公式(5)。除此之外未成熟DC发生迁移变成半成熟DC或成熟DC的迁移阈值的计算见公式(6).

算法6 计算PAMP和SS信号

输入：时序数据极差。

输出：PAMP和SS信号。

1.if |value-median|〈 std then

2.value is a safe signal；

3.SS=|median-value|；

4.PAMP=0；

5.else PAMP=|median-value|；.

6.SS=0；

7.END；

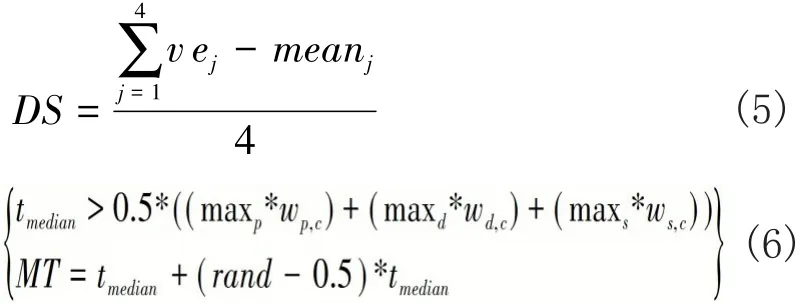
在公式(5)中,j的取值为1,2,3,4，分别代表方差，平均值，中位数，标准差四个统计属性列，在公式(6)中，maxp，maxd，maxs表示 PAMP，DS，SS信号的最大值。wp,c，wp,c，ws,c表示 PAMP，DS，SS 映射到CSM的权重。最终MT在tmedian的±50%区间内随机取值。由于5个属性列数值范围并非处于同一个级别，因此在计算输入信号之前，必须对其进行归一化，计算方法如公式(7)所示。

3 EDCA算法实验

3.1 实验数据

实验数据集来源于上海市某隧道工程项目，该数据集收集了施工过程中盾构密封舱土压力值。土压力值是重点的监测对象。对土压力值进行异常分析可以改进工程风险管理。表2为本实验的基本信息，本实验选取了该工程中2008年5月1日至2008年5月25日共11721条土压力数据作为数据样本。

表2 盾构密封舱土压力值数据集

3.2 实验环境

实验采用的计算机环境为：Intel®Core™处理器，主频为2.5GHZ，8GB内存，1T硬盘。操作系统为64位Windows 10，所有算法均由MATLAB软件实现。

3.3 算法实验及结果分析

本文对实验数据进行预处理，将同一天的数据平均分成24块，求出每块数据的最大土压力值，作为整点时刻的土压力值。例如：2008-5-1的数据平均分成24块，第一块的最大土压力值就是2008-5-1 0：00的土压力值，第二块的最大土压力值就是2008-5-1 1：00的土压力值，以此类推。预处理后的隧道工程土压力数据如图5所示。

图5 土压力分布图

为了从土压力数据源提取输入信号，应用SABE算法对工程时序数据进行分割，分别不同窗口长度下的熵极差，并绘制熵极差和对应窗口长度的关系，如图6所示。

图6 熵极差与窗口长度的关系

从图6可以看出最大熵极差出现在窗口长度L=14，最大熵极差为1.5774，此时该工程时间序列集分割成42个抗原。本实验选择表1的权值矩阵，设定异常阈值a =0.657，应用EDCA算法计算当前42个抗原的成熟环境抗原值MCAV，将MCAV大于异常阈值的抗原对应的时间子序列标记为异常，结果显示第29,30,32个抗原处于异常状态，实验结果如图7所示。通过对比查看原始数据，第29,30,32个抗原对应的数据发生的时间段为 2008-5-17 7：00～2008-5-18 10：00和 2008-5-19 1：00～2008-5-19 14：00。第一个时间段比灾害发生时间提前了1～2天，第二个时间段比灾害发生时间提前了几个小时，表明EDCA算法能够有效地捕捉异常。