多元函数微分学的基本概念内在关系中的反例

赵继红

(宝鸡文理学院 数学与信息科学学院，陕西 宝鸡 721013)

多元函数微分学是高等数学教学的重点和难点之一[1-2]。虽然其基本思想来源于一元函数微分学, 是在其基础上的推广和延伸。但多元函数微分学涉及到的概念众多, 相互之间的关系错综复杂, 较之一元函数有联系更有很大差别, 这就需要初学者对多元函数微分学中的概念、公式和定理有更深层次的理解和掌握, 而不能想当然的将一元函数的知识照搬过来。文献[3-5]已就多元函数连续、偏导数和微分这些重要概念间的相互关系、反例教学、如何理解和掌握这些概念做了系统地总结和归纳。本文主要借助于反例来厘清多元函数微分学中的一些重要概念之间的关系, 包括重极限、累次极限、连续、偏导数、微分以及方向导数。可以看出, 反例在揭示多元函数概念之间的内在关系、掌握定理、理解公式和证明伪命题等方面有着巨大功效。通过这些反例, 教师在教学环节可以更好地培养学生对概念的理解能力、辨析判断能力、发散思维能力、逆向思维能力和创新思维能力。下面以二元函数为代表展开讨论, 二元以上的多元函数可以得到类似的结论。

1 重极限和累次极限的关系

例2 考虑函数f(x,y)=

注：由例1和例2可知, 重极限存在不能保证两个累次极限存在。反过来, 两个累次极限存在也不能保证重极限存在。

2 连续和偏导数的关系

例4 考虑函数f(x,y)=

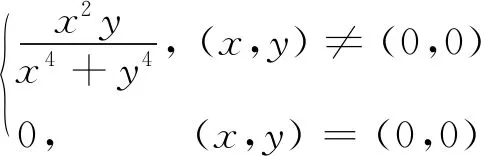
(2)按定义可求得fx(0,0)=

注：由例3和例4可知, 函数的连续性不能保证偏导数存在。反之偏导数存在也不能保证函数的连续性。注意这和一元函数连续和导数之间的关系是有本质区别的。

3 连续、偏导数和微分的关系

例5 考虑函数f(x,y)=

(2)按定义计算可得fx(0,0)=

由例2可知上式右端极限不存在, 所以函数f在(0,0)点不可微。

例6 考虑函数f(x,y)=

证 (1)先来计算函数f在(0,0)点的偏导数。当(x,y)≠(0,0)时, 易知

当(x,y)=(0,0)时，按定义可求得

同理可求得fy(0,0)=0。再来计算函数f在(0,0)点的全增量

Δz|(0,0)=f(0+Δx,0+Δy)-f(0,0)=

容易计算

从而函数f在(0,0)点可微。

注：由二元函数可微的必要条件可知,若函数f在(x0,y0)点可微, 则函数f在(x0,y0)点处连续且偏导数fx(x0,y0)和fy(x0,y0)均存在;再由可微的充分条件可知,若函数f的偏导数在点(x0,y0)的某领域内存在，且偏导函数fx和fy在点(x0,y0)处连续，则函数f在点(x0,y0)处可微。例5告诉大家即使二元函数连续且偏导数存在也不能保证其可微性, 这和一元函数可导与可微等价是有区别的, 需要特别注意区分；例6告诉大家二元函数的可微性并不能保证两个一阶偏导函数的连续性。

4 连续、偏导数、微分和方向导数的关系

例7 考虑函数f(x,y)=

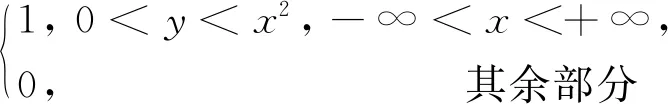
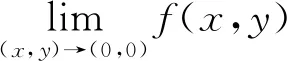
(2)注意到在始于原点的任何射线l上都存在包含原点的充分小的一段, 在这一段上f的函数值恒为零。于是按方向导数的定义, 在原点处沿任何方向l都有f的方向导数等于零。

证 按方向导数的定义可得

同理可求得f沿方向(0,1)的方向导数为1, 沿方向(-1,0)的方向导数为-1, 沿方向(0,-1)的方向导数为-1。但由例3可知偏导数fx(0,0)和fy(0,0)均不存在。

注：由可微的必要条件可知若函数f在点(x0,y0)处可微, 则函数f在点(x0,y0)处沿任一方向的方向导数都存在。例7告诉大家即使所有的方向导数都存在，也不能保证其连续性和可微性；例8告诉大家方向导数也不能保证偏导数的存在性。当然反过来偏导数的存在性更不能保证方向导数的存在性。

多元函数微分学是高等数学的重要教学内容, 其中多元函数的极限、连续、偏导数、微分和方向导数的概念和它们之间的关系, 又是多元函数微分学教学中的关键和核心所在。本文通过反例来阐明这些概念间的关系和联系, 旨在促进学生对这些基本概念的认识、理解、掌握和熟练应用, 从而更深层次的厘清它们之间的内在关系, 促进学习效率, 提高学习积极性, 达到丰富和提升对多元微分学理解层次的深度和厚度。