基于状态空间法的轨道不平顺与车体横向加速度关联模型

牛留斌,刘金朝,曲建军,尹 峰

(中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081)

轨道不平顺是引起车辆振动的主要来源，轨道的平顺性好坏直接影响车辆高速运行平稳性和舒适性。车体振动加速度是衡量车体振动程度的量度，是轨道不平顺输入特征及车辆动力学响应特性的综合反映。两者之间关联的研究有助于深入理解车辆的传递特性、找出车辆敏感波长、避免车辆振动加剧。同时，结合车辆振动和轨道不平顺综合评价轨道质量状态，有利于全面分析轨道病害，科学指导工务养护维修。因此，国内外对轨道不平顺与车体振动之间关联展开了大量的研究。文献[1-2]采用传递函数或短时傅里叶变换小波分析技术研究轨道不平顺与车辆振动响应信号之间关联；文献[3-4]通过车辆-轨道耦合动力学理论及频率分析方法研究轨道不平顺与车体振动之间的传递特性。以上研究多是采用信号处理方法(如相干分析等)或车辆-轨道动力学理论借助频谱分析研究轨道不平顺与车体振动加速度之间的关联，侧重于找出引起车体强烈振动的单项轨道不平顺敏感波长定量分布，不能给出轨道不平顺与车体振动之间的显式传递特性。车体振动是由轨道不平顺引起的综合响应，在近似的情况下，单项轨道不平顺引起的车体振动起到主要因素，如文献[5]利用系统辨识方法建立ARX模型研究轨道长波高低不平顺与车体垂向加速度之间传递关系。但相对于轨道长波高低不平顺和车体垂向加速度之间近似线性的传递关系，轨道不平顺与经过车辆一、二系悬挂传递后的车体横向加速度之间存在着较为复杂的非线性传递特性，单项轨道不平顺对车体横向加速度的影响随着频段而不同，这使得两者的传递关系更为复杂，文献[5]中的ARX模型不能有效地表征两者之间的传递关系。

本文基于系统辨识理论，以我国某列高速综合检测列车在某高速铁路上的实测轨道不平顺及车体横向加速度数据为基础，采用多输入单输出状态空间(State-space)模型建立轨道不平顺与车体横向加速度之间的关联模型研究两者之间的传递关系。利用状态空间模型的传递函数及实测轨道不平顺对车体横向加速度进行预测，并与文献[5]中ARX模型预测车体加速度结果进行了对比。

1 关联模型构建

本文构建的轨道不平顺与车体横向加速度之间的状态空间模型是系统辨识理论中的方法之一，是在不使用系统结构本身固有参数和内部复杂传递关系的基础上，通过实测得到的输入输出数据来辨识系统的传递特性。首先利用相干分析法找出不同频段上轨道不平顺与车体横向加速度之间的相干特性，为不同频段的状态空间模型选择合适的输入输出波长；再根据高速综合检测列车实测数据选择关联模型的合理阶数及相应的模型参数；最后利用残差及相关系数对关联模型进行验证。

1.1 分频段方法

车体横向加速度是由不同类型的轨道不平顺引起的，同一类型的轨道不平顺的不同波长成分将影响着车体横向加速度的不同频段[6]。为了简化模型输入变量，在轨道不平顺有效测试波长范围内，根据轨道不平顺与车体横向加速度之间的相干特性找出不同频段上与车体横向加速度相干较强的模型输入，将状态空间传递模型分为低频和中高频两个频段。相干函数[7]能够表征模型输入与输出之间的相干特性，可以反映轨道不平顺u和车体横向加速度y之间的在不同频段上的依赖程度。相干函数Cuy为

( 1 )

式中：ω为空间频率，m-1；Guy(ω)是轨道不平顺输入u和车体横向加速度输出y的互功率谱，mm·m2/s2；Guu(ω)为模型输入轨道不平顺u的自功率谱，mm2·m；Gyy(ω)为模型输出车体横向加速度y的自功率谱，m3/s4。自功率谱及互功率谱的分析方法参考文献[7]。本文采用平均周期图谱法(Welch韦尔奇)进行功率谱计算，段内傅里叶变换点数是4 096，加汉明窗(Hamming)，段与段间数据样本重叠50%。

相干函数的取值范围在0～1.00之间，相干函数值越接近1.00，说明模型输入与输出之间的依赖性越强。通常认为相干函数值大于0.80时，输出与输入之间存在有较强的相干关系。

1.2 状态空间模型

在状态空间模型中，轨道不平顺输入u和车体横向加速度输出y之间的关系表述[8-9]为

( 2 )

式中：u(t)为t时刻的轨道不平顺输入，mm；y(t)为t时刻车体横向加速度输出，m/s2；x(t)为状态空间模型的状态变量；v1(t)和v2(t)为t时刻模型误差值；A、B、C、D为状态模型待估参数。在本文中通过子空间算法得到模型待估参数，假定空间状态模型的阶数n、模型输入输出的个数分别为m和r，则参数矩阵A为n×n矩阵、B为n×m矩阵、C为r×n矩阵、D为r×m矩阵。

空间状态模型输入u和输出y之间的传递函数为

G(ω)=C(ωIn-A)-1B+D

( 3 )

式中：In为n阶单位矩阵。

由实测数据训练模型参数A、B、C、D，根据式(3)得到模型传递函数，再由模型传递函数及实测轨道不平顺数据预测相应的输出，公式为

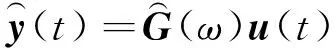
( 4 )

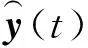
1.3 模型参数优化方法

状态空间模型参数A、B、C、D是通过实测轨道不平顺数据与车体横向加速度数据训练估计得到的，选择合理的模型阶数有利于优化模型参数的数量，提高系统辨识精度，减少模型误差。

定义模型的损失函数V为

( 5 )

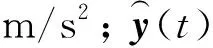
由式(5)可知，损失函数是待估参数A、B、C、D的函数，最优化预测模型的合理阶数n应使模型损失函数V最小。获得模型最小损失函数的判别方法有FPE(Final Prediction Error)准则或AIC(Akaike Information Criterion)准则[8]，其表达式分别为

( 6 )

( 7 )

式中：ΔFPE和ΔAIC分别为FPE准则和AIC准则计算出的最小误差值；d为模型中待估参数个数；N为估计模型参数所使用的实测数据样本个数；V为由式( 5 )定义的模型损失函数。

通过FPE准则或AIC准则，可以得到合理阶数的状态空间模型及对应的模型参数。

1.4 模型精度验证

为了确保所构建的状态空间模型能够应用于实际预测并保持较高的预测精度，一般采用模型预测与实测数据之间的残差及相关系数来检验状态空间模型的精度。

( 8 )

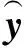
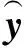
( 9 )

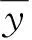
相关系数ρ的绝对值为0～1.00；当相关系数ρ的绝对值大于0.80时，认为两组数据之间具有较强的线性相关性。

2 数值试验

车体横向振动不但与轨道不平顺有关，还与车辆系统的动力性能、车轮踏面圆顺度等因素有关，所建立模型反应了轨道不平顺与车体横向加速度之间的传递关系。由于不同的检测车辆在动力性能上的差异，利用不同检测车辆上的实测数据建立模型时得到的传递函数会有差异。

车轮踏面圆顺度会引起车辆周期性振动，基波的波长与车轮轮径有关，不大于3 m，在建构模型时会将该波长成分滤除。车轮圆顺度引起的二阶及以上谐波成分在总成分中的比例很少，对模型的建构没有影响。

本文中轨向不平顺是指实测左右两侧轨向不平顺的平均值；由于轨道短波不平顺引起激振频率高，对车体振动加速度影响不大，因此忽略3 m以下轨道不平顺对车辆横向加速度的影响，主要考虑中长波范围轨道不平顺与车体振动之间的关系，所以在数据使用前首先对实测车体横向加速度数据进行了空间频率为0.35 m-1的低通滤波，保留了大于3 m的波长成分，轨道检测数据的采样间隔为0.25 m，车辆检测速度为200 km/h。

利用构建模型的传递函数及实测轨道不平顺数据对车体横向加速度进行预测，结果与实测数据的相关性对比是验证模型辨识精度的方法。所以将实测数据分为两个相互独立的部分：一部分用于辨识训练关联模型的参数，样本数N为10 000组；另一部分轨道不平顺数据及关联模型用于预测车体横向加速度，并与实测车体加速度数据进行对比。

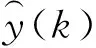
2.1 状态空间模型分频段相干函数

高速综合检测列车实测车体横向加速度功率谱曲线和车体横向加速度与长波轨向不平顺、曲率、超高、水平等的相干函数曲线，见图1。由图1可知，车体横向加速度在空间频域上的能量分布比较集中，主要分布在空间频域0.010～0.050 m-1范围内。在低于0.005 m-1的频段时，车体横向加速度与超高及曲率相干函数值大于0.80；在0.005～0.008 m-1频段时，车体横向加速度与水平相干函数值较大；在0.008～0.35 m-1频段，车体横向加速度与长波轨向不平顺相干函数值较大。

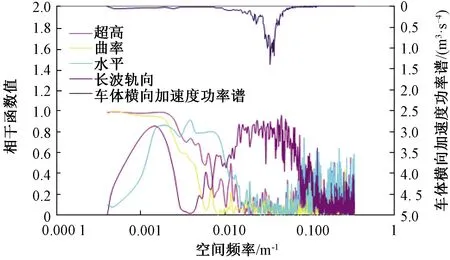
图1 高速综合检测列车车体横向加速度功率谱及相干函数

在不同的频段，不同类型的轨道不平顺与车体横向加速度的相干特性是不一样的。分为不同的频段有助于建立不同类型轨道不平顺与车体横向加速度之间的状态空间模型。由图1可知，本文分别在小于0.005 m-1频段和0.005～0.350 m-1频段，在低频区段，状态空间模型的输入为曲率和超高；中高频区段，状态空间模型的输入为长波轨向和水平。低频模型是对实测数据0.005 m-1低通滤波得到的；中高频数据是对实测数据频率为0.005～0.350 m-1带通滤波得到的。

2.2 低频状态空间模型

由式(7)AIC准则公式计算值与状态空间低频车体横向加速度关联模型阶数n之间的曲线见图2，图2中当模型的阶数n选为6时，对应的模型AIC准则值最小。所以，在建立中高频横向加速度与轨道不平顺之间的状态空间关联模型时，选用的阶数n为6，所建模型的传递函数特性曲线见图3，幅频特性曲线变化平缓，相频特性曲线显示两者没有相位差。

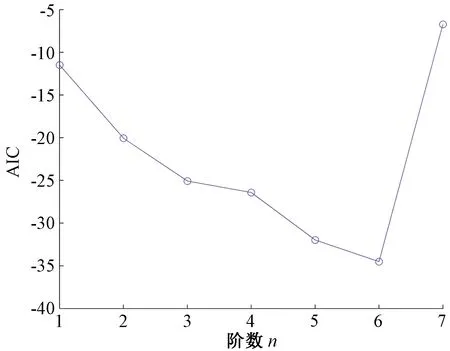
图2 状态空间模型AIC与阶数关系图(低频)

图3 状态空间法传递函数特性(低频模型)

利用状态空间模型传递函数及实测曲率、超高数据预测的车体横向加速度与实测加速度的对比图见图4。图4中显示了直线及曲线线况条件两者波形吻合良好，其相关系数为0.98，直线部分的对比见图5。

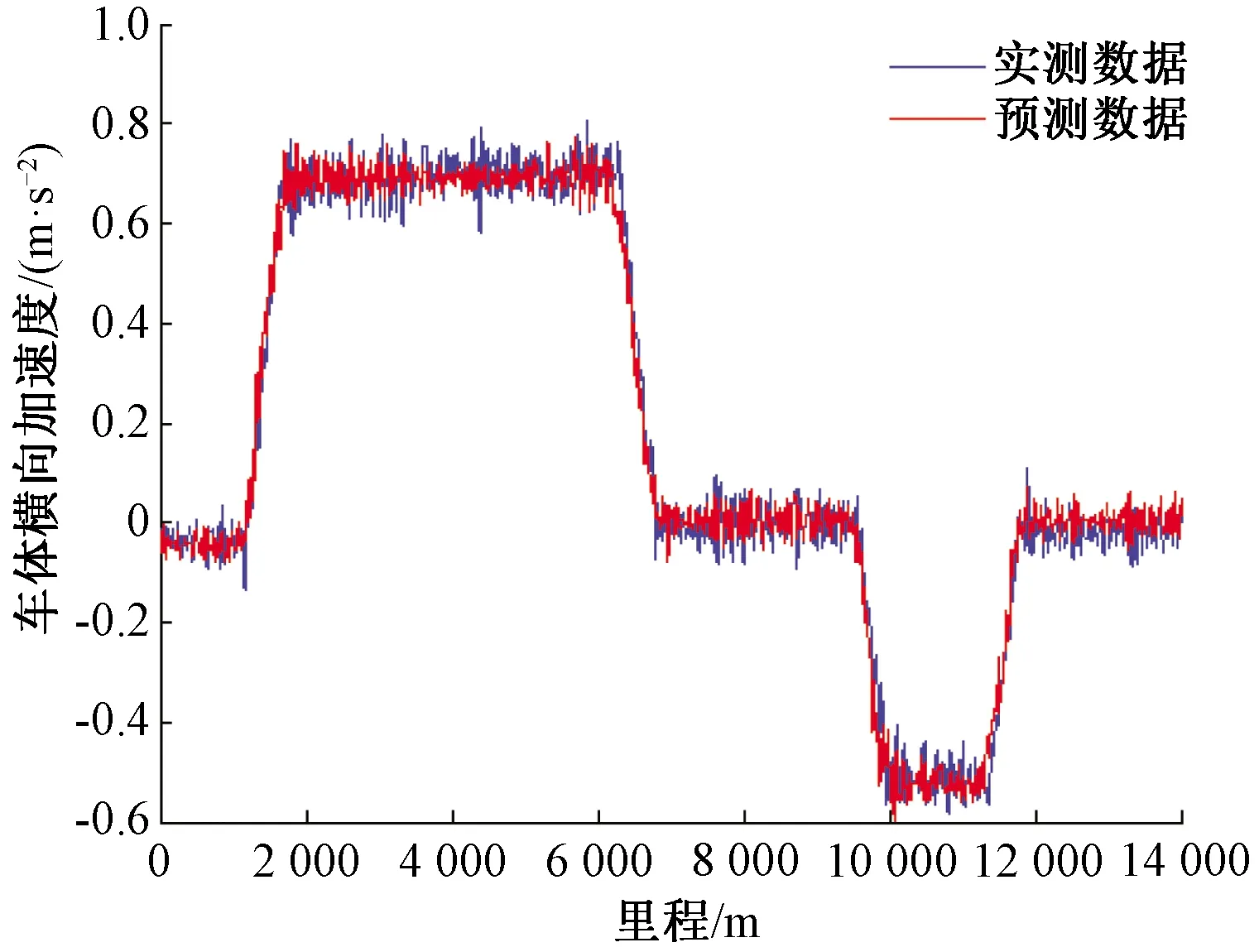
图4 状态空间法预测低频车体横向加速度及对比

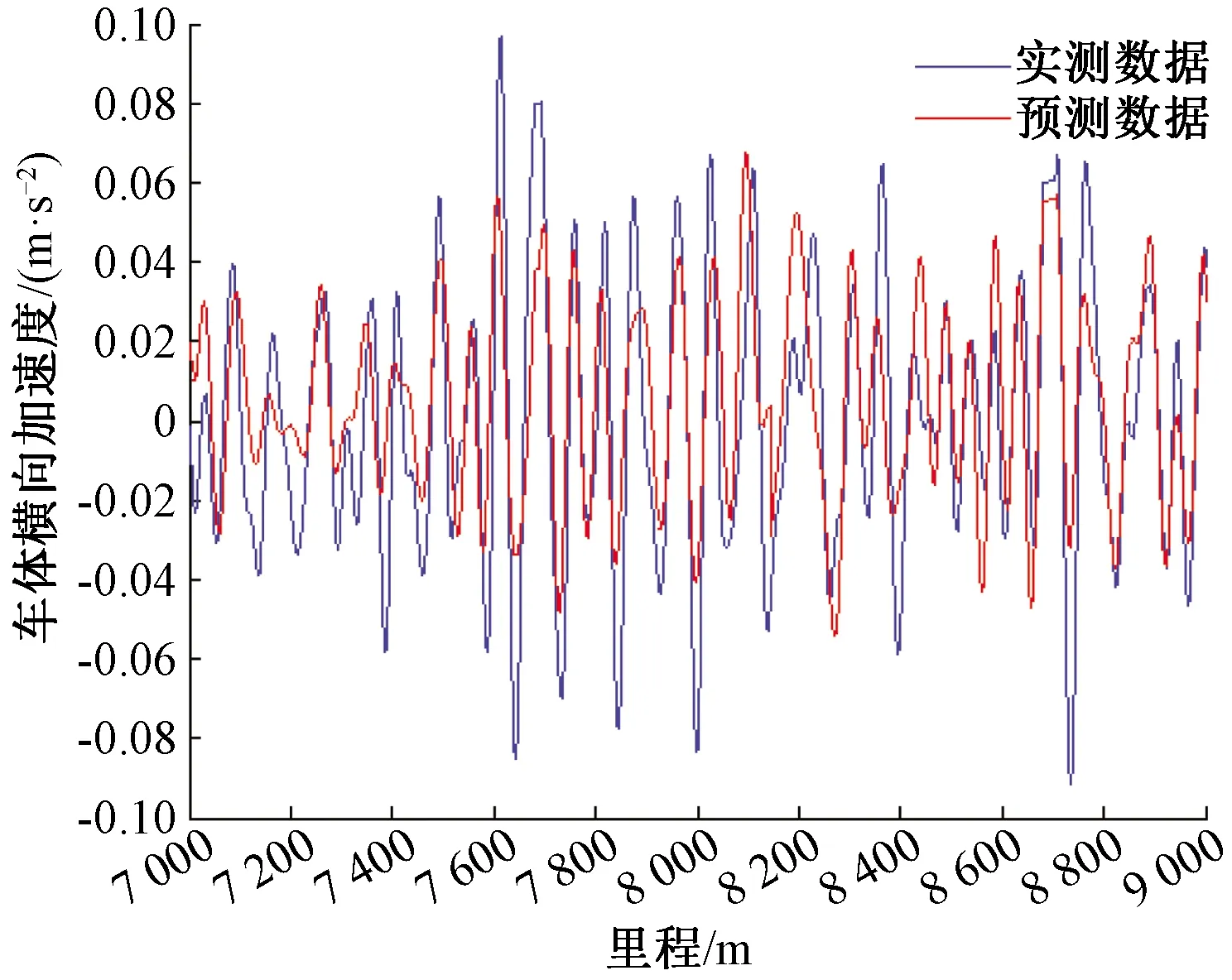
图5 状态空间法预测低频车体横向加速度及对比(直线区段)

两者的残差re服从正态分布N(-0.001 3，0.004 6)，近似满足0均值假设，其正态概率分布曲线见图6。

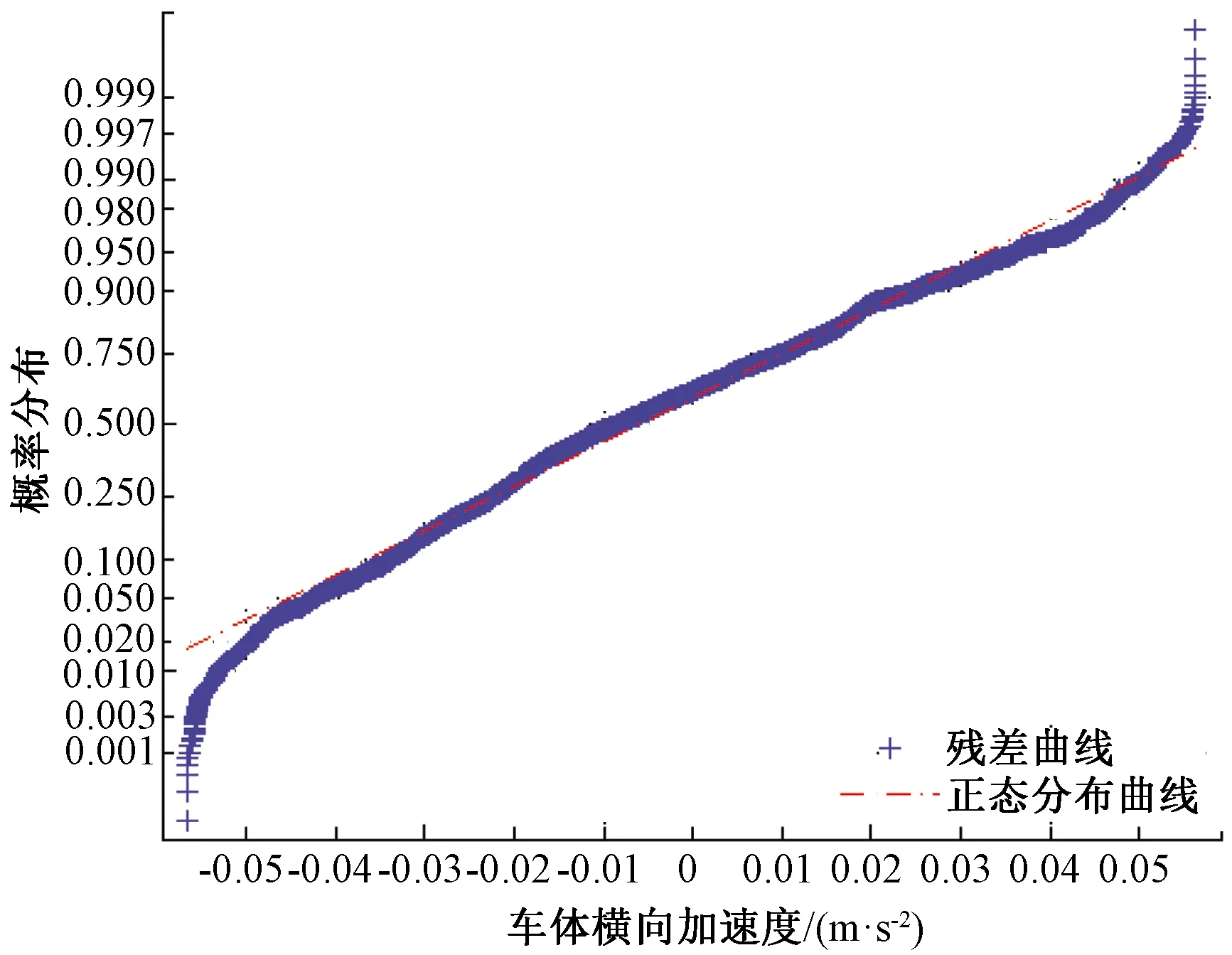
图6 状态空间模型残差分布图

2.3 中高频状态空间模型

中高频状态空间模型的阶数是通过AIC准则进行优化定阶的，按式(7)AIC准则公式计算值与状态空间模型阶数n之间的关系曲线见图7，图7中曲线表明，当状态空间模型的阶数n选为6时，对应的模型AIC准则值最小，模型最合理。所以，在建立中高频横向加速度与轨道不平顺之间的状态空间模型时，选用的阶数n为6。

在0.005～0.350 m-1频段利用状态空间法建立长波轨向不平顺、水平与车体横向加速度之间的多输入单输出(MISO)关联模型，由式(2)得到模型输入与输出之间的传递函数幅频特性与相频曲线见图8，两者的相频特性曲线上在0.047、0.062、0.21 m-1处出现了相位由-π到π的突变，在利用模型传递函数预测输出时将造成该频段预测数据的不准确。

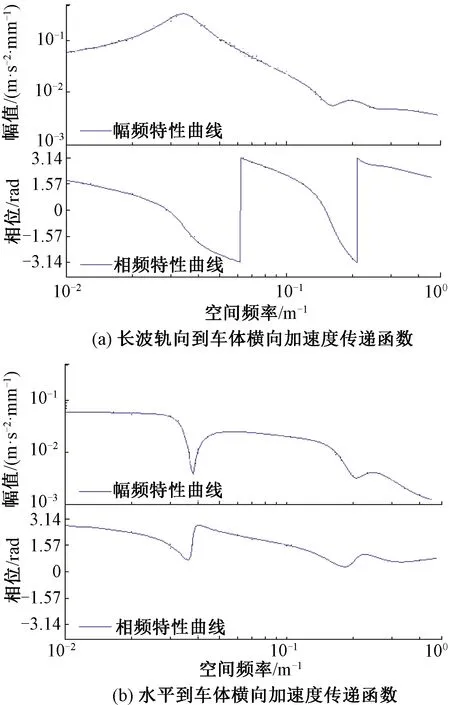
图8 状态空间法传递函数特性(中高频)

利用6阶状态空间模型传递函数及实测轨道长波轨向、水平预测到的车体横向加速度，并与实测车体横向加速度进行了对比，见图9，两者的相关系数为0.85，两者的残差服从正态分布N(0.000 3，0.006 3)，满足残差近似0均值假设，方差0.006 3反映了模型残差偏离零均值的程度较小，模型输出值与实测值很接近。残差正态概率分布曲线见图10。

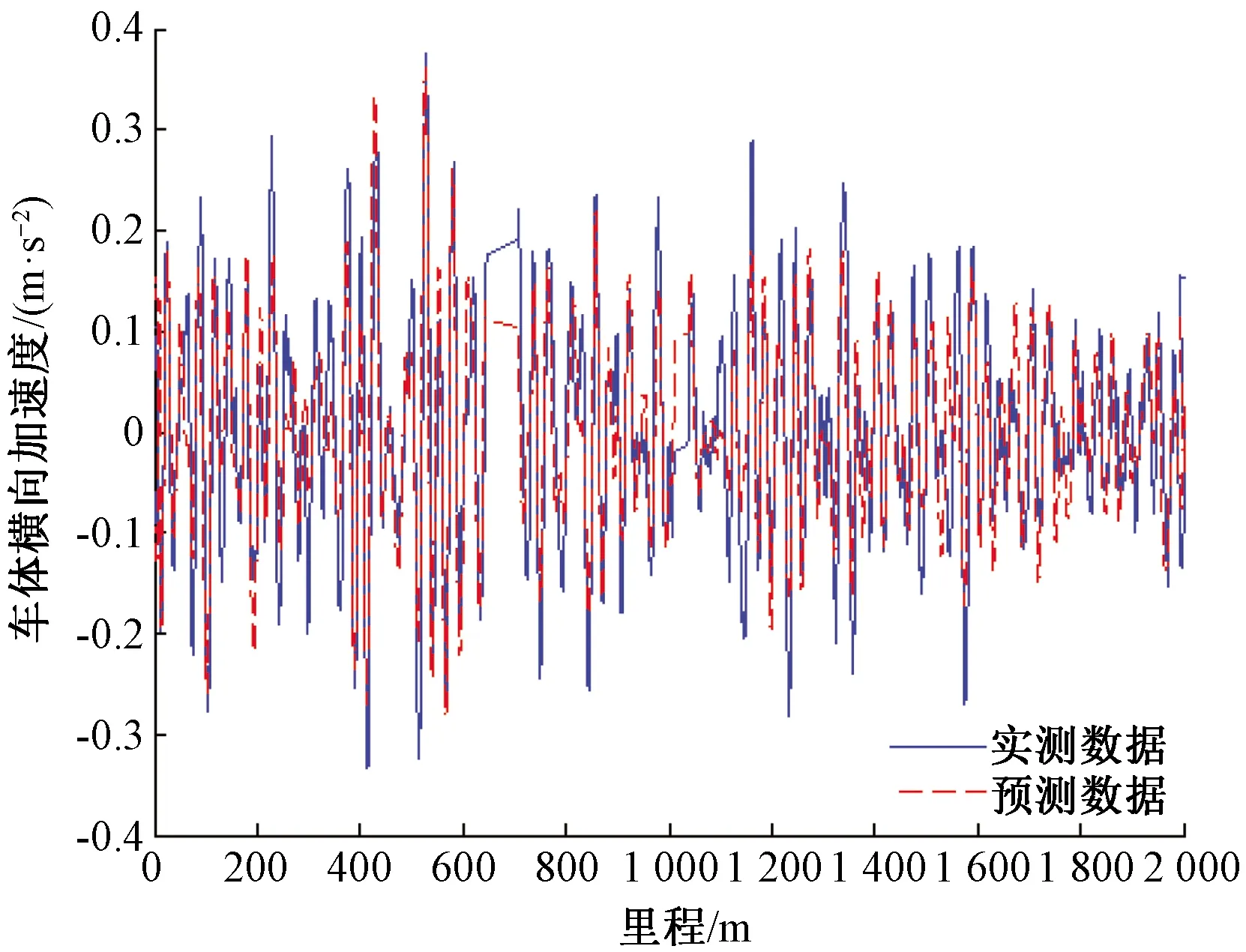
图9 中高频横向加速度预测结果图(圆曲线部分)

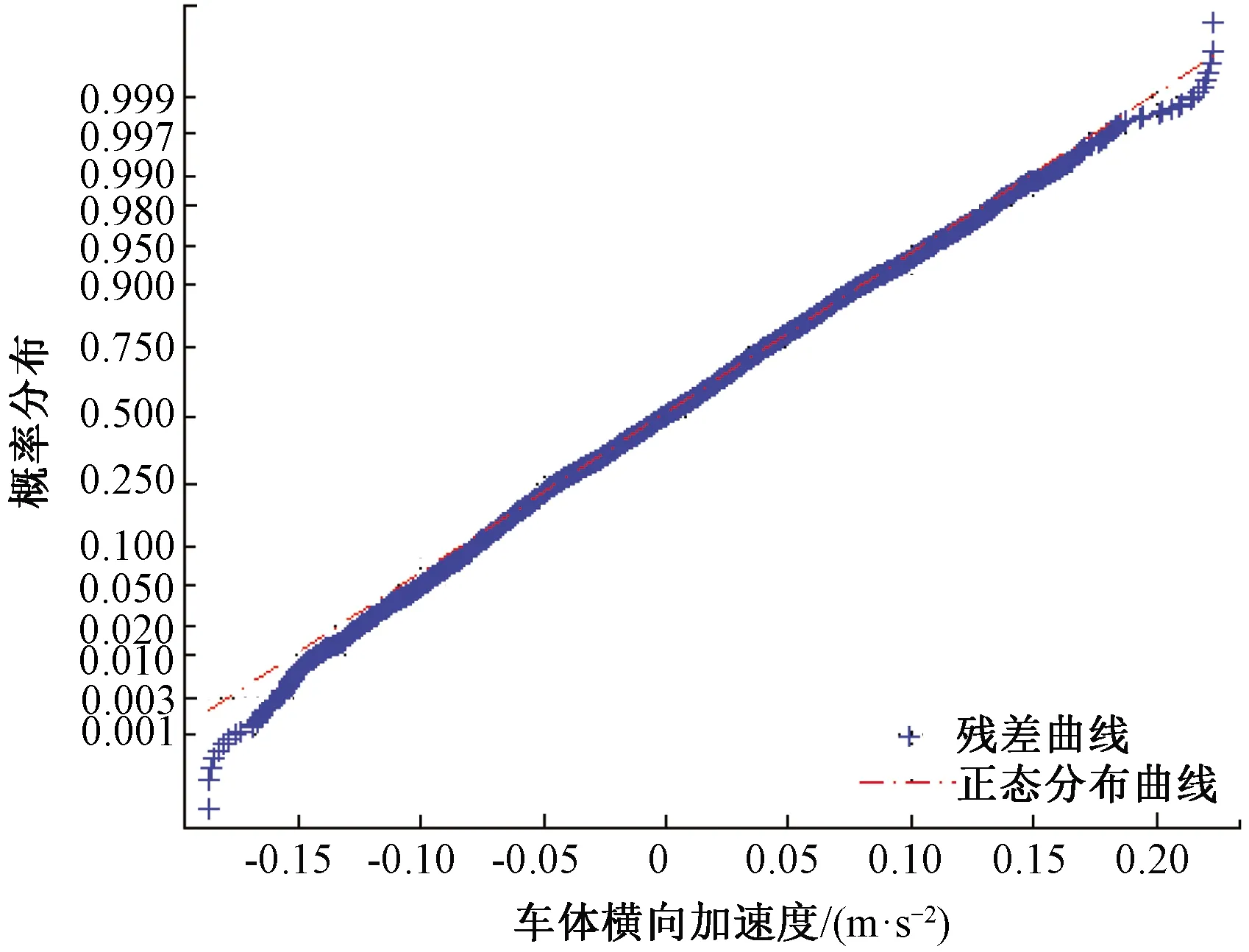
图10 中高频残差分布曲线

利用n阶状态空间模型预测车体横向加速度时，前n个初始值设置为0，在开始预测第n+1个值时，存在较大的误差，经过20至40步的迭代计算，预测车体横向加速度数据将逐渐收敛于实测波形。

除了在个别高频数据外，利用空间状态模型预测的车体横向加速度与实测车体横向加速度吻合良好，两者之间的相关系数较高，存在着较强的线性相关性。

传递函数能够反映状态空间模型能够辨识轨道不平顺与车体横向加速度之间关联关系的准确性，而传递函数的正确性可以通过实测数据进行验证。

3 模型验证及对比

利用实测轨道检测数据及状态空间关联模型传递函数预测车体横向加速度，并与相应的实测车体横向加速度结果进行对比。利用ARX模型建立轨道不平顺与车体横向加速度关联模型的方法可参考文献[5]。图11、图12分别利用状态空间模型传递函数、ARX模型传递函数并与相应的实测车体横向加速度进行对比。图11、图12中所选用的样本数据区段长度为1 500 m，曲线半径为12 000 m，共有6 000个样本点。

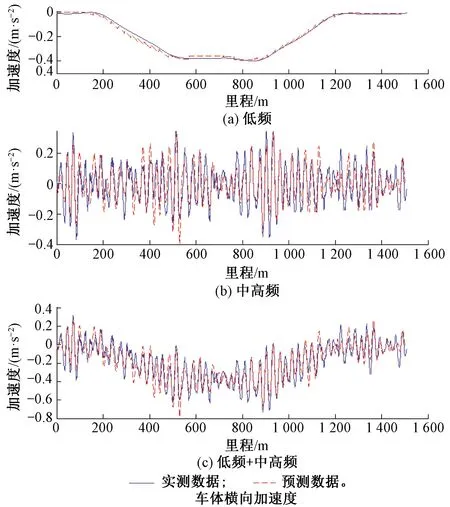
图11 状态空间模型预测车体横向加速度数据与实测数据对比图

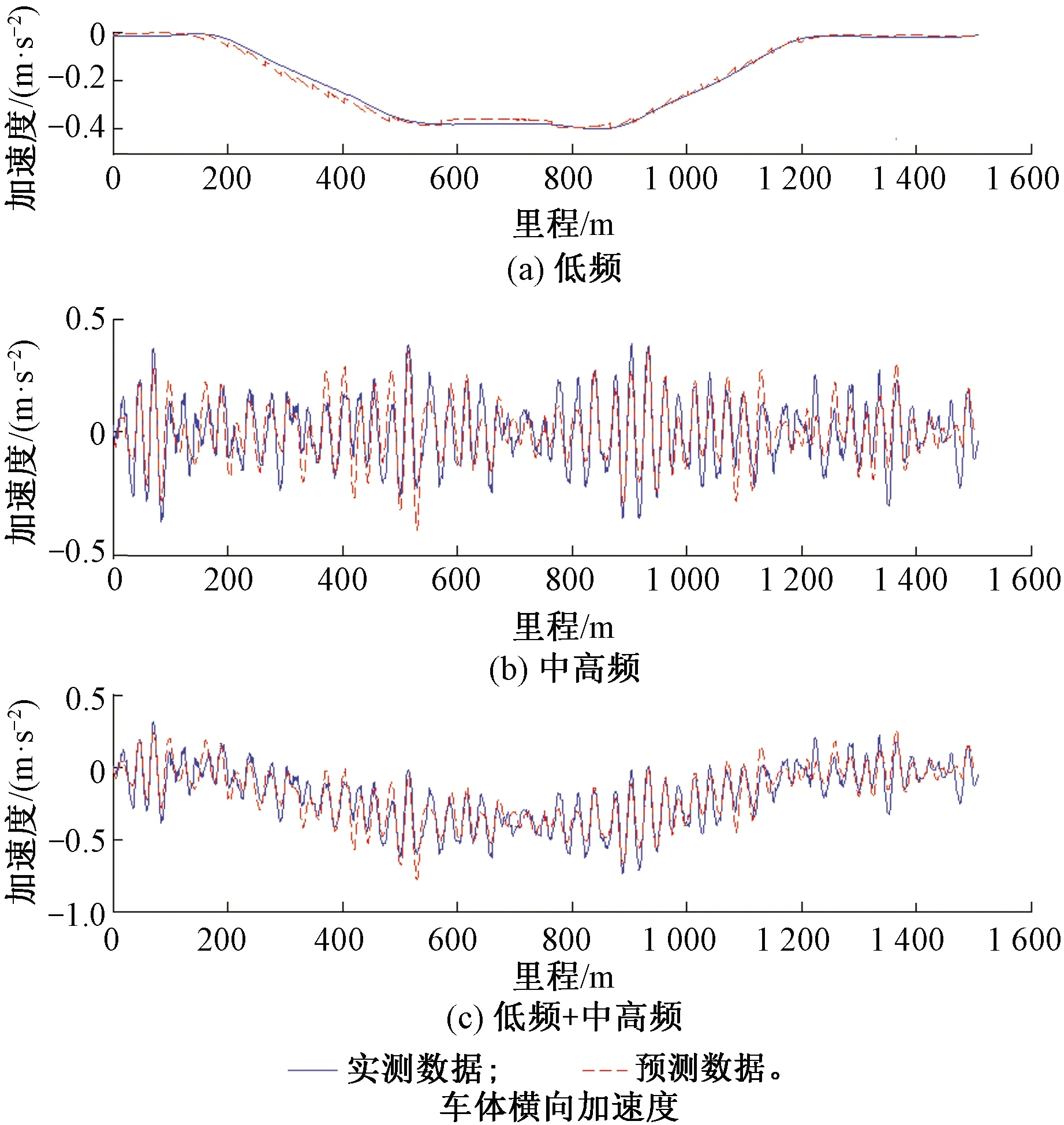
图12 ARX模型预测车体横向加速度数据与实测数据对比图

由图12可知，无论线型是直线或者曲线，状态空间模型及ARX模型预测的车体横向加速度波形与实测波形吻合一致，但状态空间模型预测的低频、中高频及整体数据与实测数据的相关系数分别为0.97、0.86、0.94，而ARX模型的相关系数分别为0.86、0.80、0.82。

由上述利用关联模型传递函数预测车体横向加速度结果与实测车体横向加速度数据对比可知状态空间模型能够较准确的辨识轨道不平顺与车体横向加速度之间的传递关系，而ARX模型辨识结果的精度有待提高。

4 结论

在轨道不平顺与车体横向加速度相干分析基础上确定状态空间模型的输入，分别在小于0.005 m-1和0.005～0.350 m-1两个空间频段上建立轨道不平顺与车体横向加速度之间的关联模型，利用高速综合检测列车实测数据训练优化关联模型得到传递模型的合理阶数及结构参数，模型的残差近似符合零正态分布的假设。

对比实测轨道不平顺及模型传递函数预测车体横向加速度数据和实测车体横向加速度结果验证所构建的状态空间模型传递函数的准确性，分析结果表明合理阶数的状态空间模型能够较好地辨识轨道不平顺与车体横向加速度之间的传递关系。