地铁列车再生制动能量利用分析与时刻表优化方法研究
2020-09-07魏润斌杨雍彬
魏润斌,杜 鹏,杨雍彬,胡 礼
(1. 北京交通大学 交通运输学院,北京 100044;2. 清华大学 交通研究所,北京 100084)
城市轨道交通具有运量大、速度快、安全准点、节能环保等特点,但在运营过程中也会产生大量的能耗,在运输组织方面通过优化列车时刻表达到节能的目的,已被证实可行并成为当下热点。早在1988年,Gordon等[1]就利用当时在开发之中的先进的列车自动控制系统(AATC),分析了使用该系统之后可以通过控制牵引、制动的顺序,实现再生制动的利用。2007年,Miyatake等[2]提出了一种考虑直流线路的列车运行能耗优化算法,详细介绍了再生制动能量的计算方法,并通过实例验证将能耗降低了4.2%~17.9%。2017年,Liu等[3]分析了不同列车控制策略模式下利用再生制动节能的效果。
基于再生制动能量利用的计算,一些节能模型也得以建立,其中很大一部分是通过优化时刻表来实现的[4-5]。Yang等[6]提出了一种以发车间隔和停站时间为决策变量、最大化列车牵引制动重叠时间为目标的整数规划模型,设计了遗传算法求解,对北京亦庄线进行实例分析,分别对高峰小时和非高峰小时进行了对比,证明了该模型的节能效率。但文中仅提高了列车运行的重叠时间,未能计算具体的再生制动能量值。于是,在重叠时间的基础上,很多学者对再生制动能量计算方法进行了深入研究,主要有三类:
第一类是通过工况重叠时间内的列车动能变化量来计算。冯瑜等[7]将单车节能与多车协同节能进行一体化设计,以发车间隔、列车运行时间、停站时间为控制变量,降低全线总能耗为目标,提出一种运行图优化方法,利用北京地铁数据进行了验证。彭其渊等[8]提出了在保证旅客运输任务的前提下优化列车开行策略提高再生制动能量利用的模型,使用惩罚函数法和解析方程方法进行求解。
第二类是通过取重叠时间内两列车的机械功率较小值来计算。Li等[9]提出了联合优化时刻表及列车速度操纵的列车综合节能运行模式(IEEO),利用亦庄线数据与文献[10]提出的EEO模型、文献[6]提出的协同调度(CS)模型进行对比,得到了更优的节能效果。柏赟等[11]提出了以列车净能耗为目标的快慢车线路列车协同操纵节能优化模型。冉昕晨等[12]考虑断面客流空间分布差异,建立了节能时刻表优化模型。
第三类是通过重叠时间内两列车的机械功率的重叠面积来计算。Li等[13]在CS的基础上提出了一种随机协同调度(SCS)的方法,该方法考虑了列车运行时间和延误时间的随机性,估计了再生制动能量利用的转化和传输损耗,建立了一个随机期望值模型,利用二进制遗传算法求解。步兵等[14]实现单车节能和多车协同利用再生制动能量策略的统一规划,建立了节能时刻表模型并用北京地铁昌平线数据进行验证。Gupta等[15]提出了一种新的两步线性优化模型来计算地铁的节能时间表,最大化再生制动能量利用,降低列车消耗总能量,并利用到上海地铁8号线进行了实例验证。
近年来利用再生制动节能的部分文献见表1。

表1 近年利用再生制动节能文献
由表1可知,既有关于再生制动能量利用的影响因素的研究尚不全面,尤其是在再生制动能量利用率影响因素上,部分学者假设再生制动能量利用没有损耗[6],多数学者则是将一个固定系数定为再生制动能量转换利用的损耗,用它乘以提供的再生制动能量得到实际使用的再生制动能量[9,13-14]。既有研究可以简化的将再生制动能量利用不完全的因素考虑进去,但实际上再生制动能量利用的损耗受到多种因素的影响,并非是固定不变的,因此,固定系数法不能很好地体现出影响因素带来的差异。本文在计算再生制动能量利用时考虑了牵引制动重叠时间分布以及前后车距离对其利用率的影响,得到了考虑因素更全面的再生制动能量计算方法,并且基于这一方法建立了以总能耗最低为目标的时刻表优化模型。
1 再生制动能量利用率影响因素
在计算再生制动能量利用的相关研究中,部分学者[13-14]通过列车牵引制动重叠时间下的牵引功率和制动功率来计算,在此基础上,为探究重叠时间分布以及前后车距离对再生制动能量利用的影响规律,本文利用列车运行仿真软件OpenTrack以及列车供电仿真软件OpenPowerNet设计了对比实验。
1.1 牵引制动重叠时间分布
列车利用再生制动能量的前提是前后两车分别处于牵引和制动工况,并且两工况在时间维度上有重合的部分。既有研究基本上都是利用重叠时间来计算利用再生制动能量,其中部分学者[6]将重叠时间直接等效为再生制动能量的利用,然而经多次仿真实验发现,重叠时间和利用到的再生制动能量只是呈现正相关关系,但并非是线性相关,并且重叠时间分布的不同也会影响列车再生制动能量的利用。在此基础上,通过控制前车制动时间,调节后车出发时间来改变重叠时间分布,得到了重叠时间分布不同情形下列车再生制动能量利用功率对比,见图1。
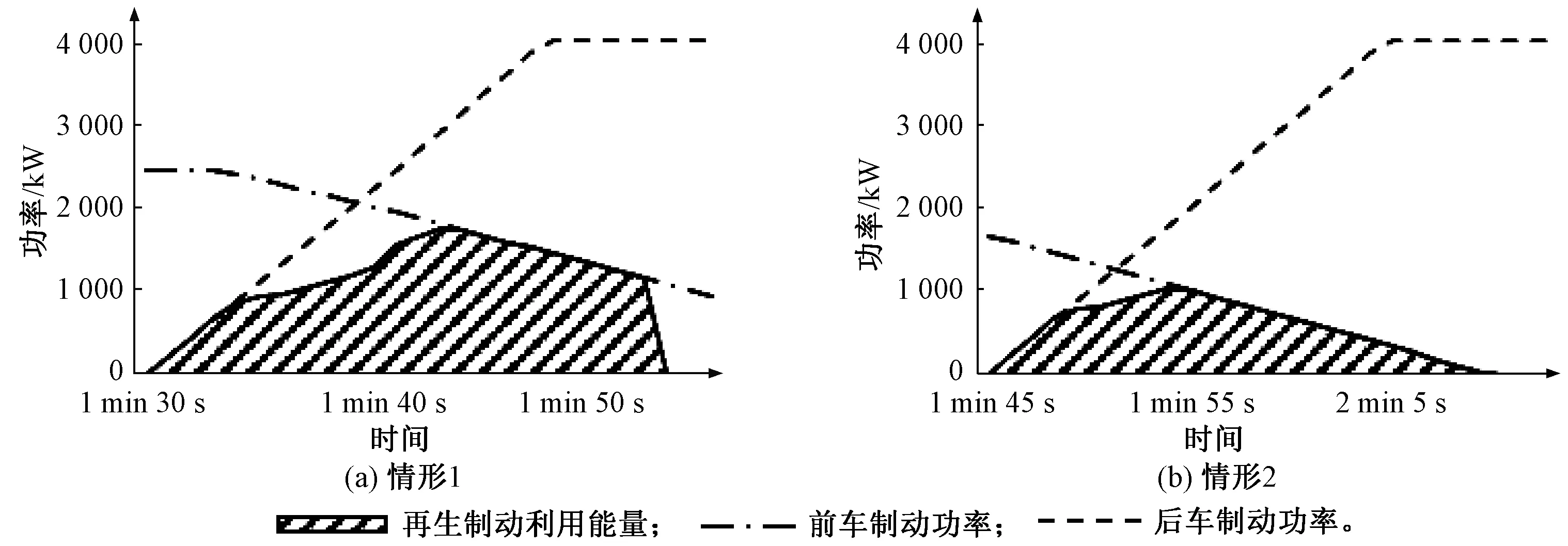
图1 重叠时间分布不同情形下列车再生制动能量利用功率图
由图1可知,利用再生制动能量的列车的牵引功率随着列车速度的提高而上升,此为牵引列车所需的能量功率,提供再生制动能量的列车的制动功率随着列车速度的降低而下降,此为制动列车提供的能量功率,所以两条曲线重叠的阴影部分为最大能利用到的再生制动能量。在两种情形下,列车工况重叠时长相同,但重叠时间分布不同,可利用到的再生制动能量也不同。而之所以重叠时间分布会影响到再生制动能量利用,是因为在任何时刻,再生制动利用功率均小于等于后车牵引功率和前车制动功率中的较小值,当图1(b)中重叠时间处于前车制动的后半段时,前车制动功率下降明显,成为了限制瓶颈。而图1(a)中重叠时间处于前车制动的前半段,前车制动功率较高,再生制动能量利用的限制也较高,可利用到的再生制动能量也越高。
综上所述,单纯地用时间重叠来表示再生制动能量利用的多少是不够完整的,只有考虑牵引和制动的瞬时功率才能更好地体现再生制动利用的效果。本文的再生制动能量利用是在基于时间重叠的前提下,考虑两车牵引和制动功率的具体数值计算得到的。
1.2 前后车距离对再生制动能量利用率的影响
本文计算再生制动能量利用时,不仅考虑重叠时间下两车机械功率的影响,同时也考虑了前后车距离的影响。当前后车距离增加时,由于电能传输损耗等原因,实际可利用到的再生制动能量小于根据前后车牵引制动功率计算得到的理想值。为体现前后车距离对再生制动能量利用率的影响,控制后车出发位置改变前后车距离,进行多次实验,得到前后车距离不同情况下列车再生制动能量利用功率的对比,见图2。

图2 前后车距离不同情况下列车再生制动能量利用功率
图2中实线表示利用到的再生制动能量的功率,由上至下分别对应了前后车距离从1.7 km以0.4 km的间隔递增到5.3 km。此处的1.7 km是实验设计的信号系统下两车之间的最短距离,5.3 km是满足最低服务水平的发车间隔下的两车最长距离。由图2可知,在前车制动功率及后车牵引功率不变的前提下,随着前后车距离的增加,列车再生制动功率不断下降,使用到的再生制动能量也随之下降。基于这一情况,整理数据得到了前后车距离与再生制动利用率百分比的散点图,见图3。

图3 前后车距离与再生制动利用率百分比关系图
分析表明前后车距离与再生制动利用能耗具有明显的相关性,散点图拟合为二次多项式函数
f(s)=(-0.053 2s2+0.24s+0.635 1)×100%
(1)
式中:s为前后车距离,km;f(s)为再生制动利用率百分比。
该拟合函数决定系数R2达到0.992 9,符合度较高,本文利用该函数建立列车时刻表优化模型。
2 模型构建
2.1 模型假设
根据城市轨道交通系统的运行特点,结合既有研究,参考文献[6-7]做出以下假设:
(1)再生制动能量利用只发生在同一供电分区内的牵引制动列车之间,由于地铁供电分区的长度限制,不存在3辆车同时处于同一供电分区的情况。
(2)不考虑上下行之间的再生制动能量利用。
(3)所有列车在同一车站的停站时间相同。
(4)所有列车在同一区间内的操纵策略相同,意味着对每一辆列车而言,在同一区间内的加速工况、惰行工况、制动工况的时间、距离、速度是一样的。
需要注意,本文假设不同于既有研究的地方是,不将再生制动能量的损耗和传输效率假设为定值,而是作为变量加入到模型计算当中。
2.2 参数及变量
本文模型所用参数、决策变量及中间变量见表2、表3。

表2 参数及决策变量

表3 中间变量
由于地铁列车站间距较短,列车操纵策略一般有牵引—恒速—惰行—制动的四阶段法和牵引—惰行—制动的三阶段法,根据文献[9]的列车操纵方式采用第二种运行策略,列车在区段n内的运行速度曲线见图4。
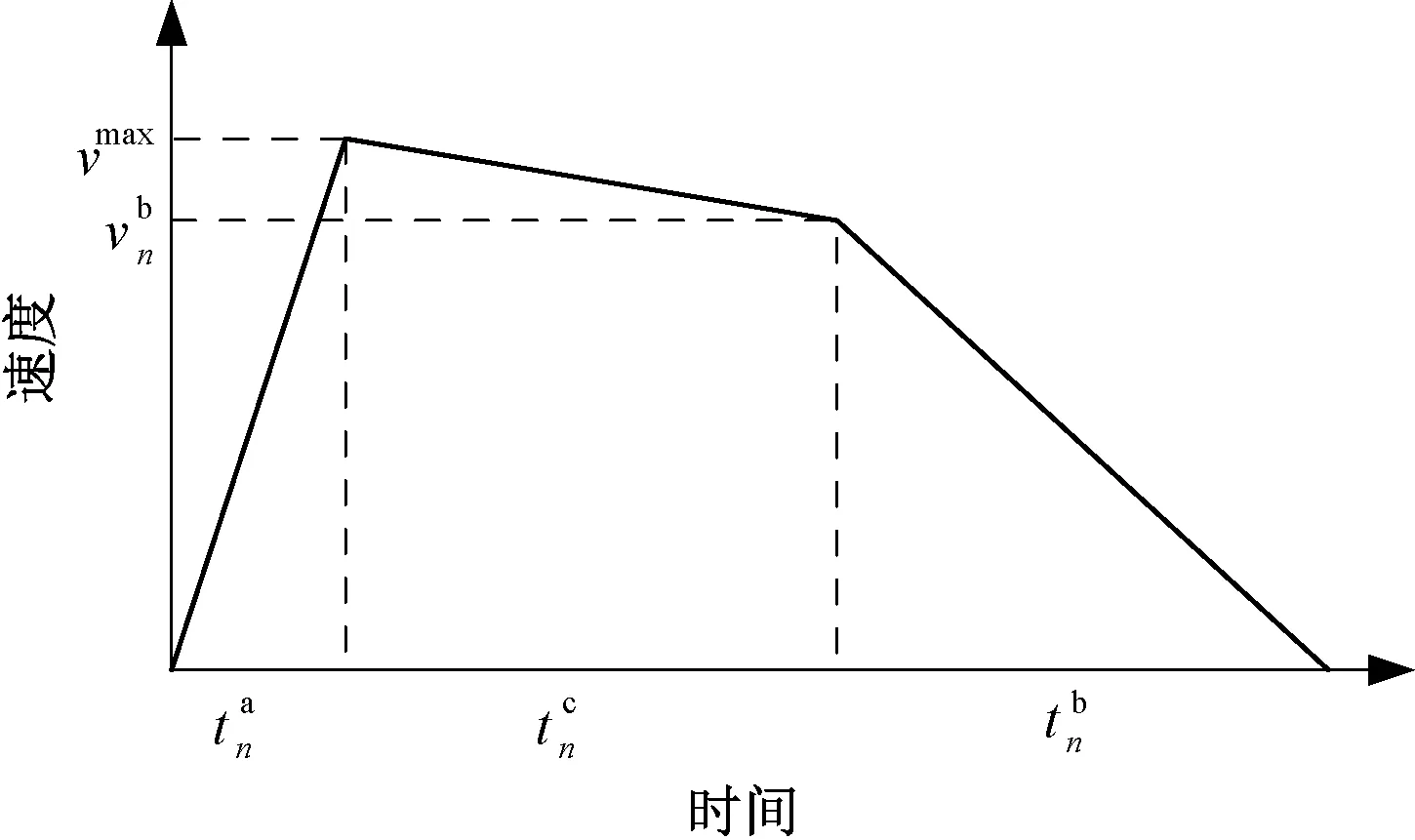
图4 列车在区段n内的速度曲线
对第i车而言,离开第m个车站的时刻
(2)
所有列车牵引运行所需能耗为
(3)
决策变量有两类:一类为停站时间xn,从x2开始至xN-1,共有N-2个;另一类为发车间隔h,决策变量总计为N-1个。中间变量τ1、τ2、Δ均为便于计算和表示而设。
2.3 目标函数
根据列车牵引、制动特性,分别得到牵引功率和制动功率与时间的曲线,见图5、图6,列车功率分为低速时与速度正相关以及高速时恒定最大功率两个阶段,所以不同的制动时长提供的制动功率不同,从而影响列车再生制动能量利用的计算。本文全面考虑列车在区间运行中处于制动工况的时长,并根据时长的不同将再生制动能量利用情况分为5种类型,划分方法为
(4)
并且在每一种类型中又根据两车重叠时间不同划分为若干个情况,汇总所有情况见表4,由于计算方法和公式重复性较大,故文中只以第一种类型为例进行详细说明。同时,列车再生制动能量利用分为前车牵引后车制动和前车制动后车牵引两个部分,两部分计算方法相近,此处以前车牵引后车制动为例进行分析。

图5 前车牵引功率-时间曲线
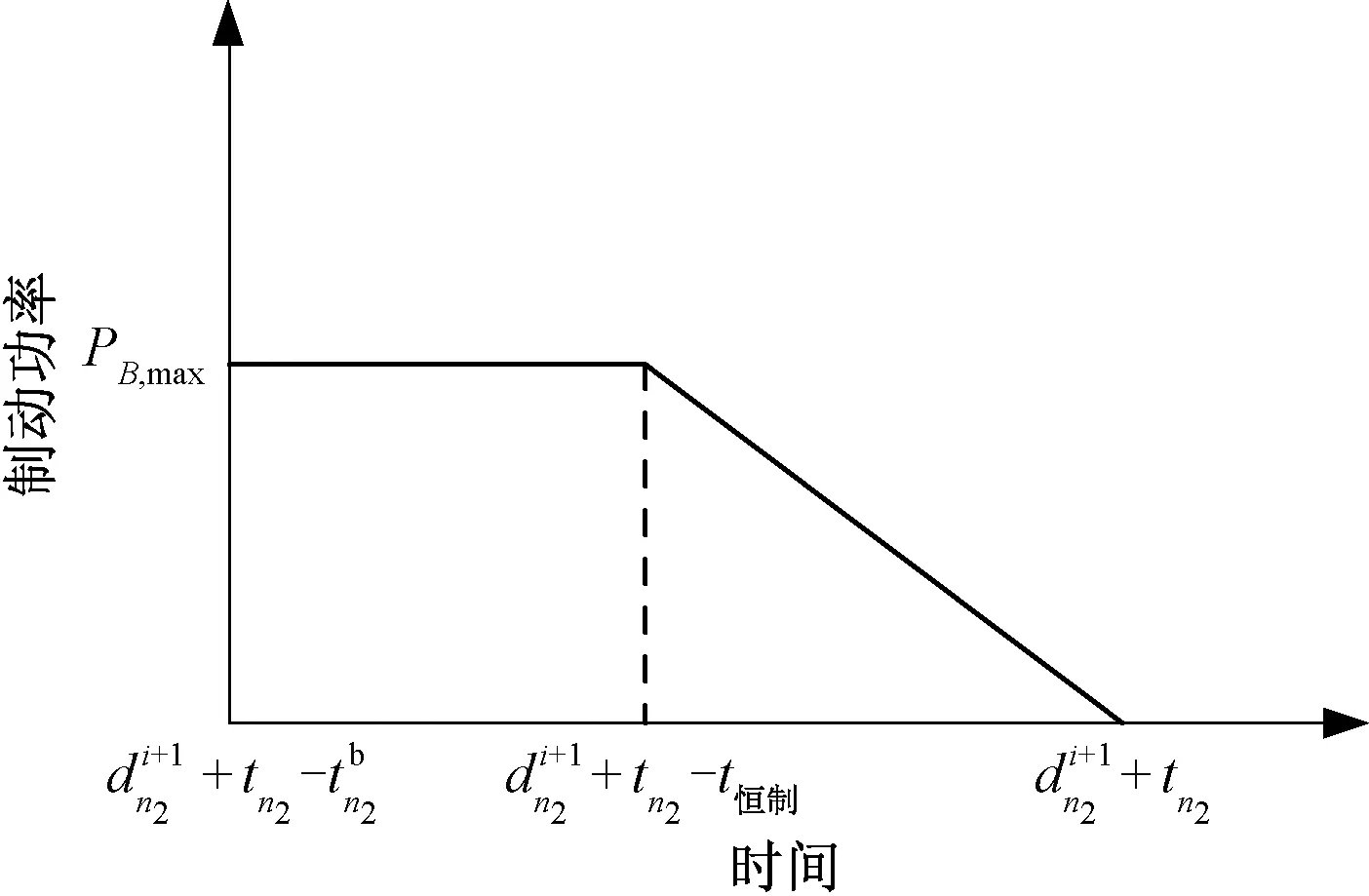
图6 后车制动功率-时间曲线
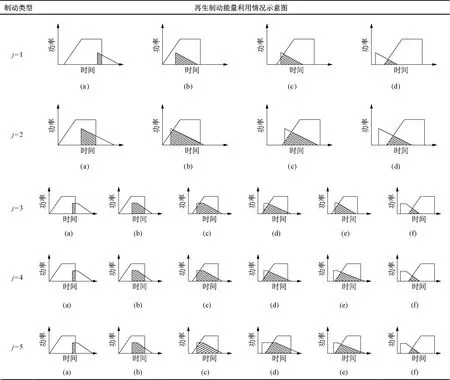
表4 不同制动时间长短下的再生制动能量利用情况
表4中j=1类型根据两车重叠时间不同可以划分6种情况(2种不重叠的情况未在表中体现),根据基于时间重叠的再生制动能量利用计算方法,可以得到
(5)
式中:τ1、τ2分别为不同情况下再生制动能量利用开始到峰值的时间段。
与E1,1的计算方法相似,可以求得其他情况下可利用的再生制动能量,用所有列车牵引运行所需能耗E0减去可以利用到的所有再生制动能量,得到所有列车运行净能耗,即为目标函数E
(6)
2.4 约束条件
(1)列车发车间隔约束:由线路条件限制列车最小发车间隔hmin,由乘客服务水平决定最大发车间隔hmax,应满足
hmin≤h≤hmax
(7)
(2)列车旅行时间约束:列车运行全程的旅行时间根据停站时间以及站间运行时间计算,结合具体的线路条件,上下限分别记做Tmin、Tmax,满足
(8)
(3)列车停站时间约束:在满足客流量需求的情况下有一定的波动空间,下限为xmin,上限为xmax,列车停站时间的下限需要满足车站客流最大乘降时间,在此基础上放宽停站时间约束的上限以此来达到通过调整停站时间进行列车运行节能的目的。列车停站时间需要满足
xmin≤xn≤xmax
(9)
3 算法求解
第2节所建的模型为非线性整数规划模型,针对此类时刻表优化问题,常用遗传算法进行求解,本文继承并使用了遗传算法和Matlab语言编程进行求解,算法步骤如下:
Step1编码
决策变量为停站时间xn和发车间隔h,使用二进制编码方法对可行解进行编码,一组可行解X=(x2,x3,…,xN-1,h)编码为C=(c1,c2,…,cN-2,cN-1),以X=(30,30,…,30,360)为例进行了编码,见图7。

图7 染色体编码
Step2生成初始种群
遗传算法设计时种群规模选取过大会导致计算时间过长,选取过小又无法找到最优解,经过多次实验发现,种群规模Nsizepop选取150次时可以最快的得到最优解。随机生成符合约束的可行解并利用Step1中方法进行编码,重复该过程150次,生成初始种群。
Step3计算适应度

Step4生成子代
②交叉:染色体两两配对,以交叉概率ppc交换随机交叉点后染色体部分,进行可行性检测,可行则代替上一代染色体,不可行则保持上一代不变。
③变异:随机选择染色体的变异位置,按变异概率ppm将0-1值互换形成新的个体,进行可行性检测,可行则代替上一代染色体,不可行则保持上一代不变。
Step5终止条件
重复Step3~Step4,直到迭代次数达到预设最大值100,输出当前种群中最优个体编码及目标值,进行染色体解码得到最优的停站时间与发车间隔方案。
4 案例分析
为验证模型与算法的准确性,用北京地铁某线路数据作案例分析[9]。该线路共14个车站,6个变电所,站间距及变电所覆盖范围见表5,现行的各站发车时刻表见表6。列车采用6节编组(3M3T),总质量为287 080 kg,最大速度为80 km/h。根据发车间隔的不同,分为高峰时段(150~240 s)和平峰时段(240~360 s)两种情况进行案例实验。
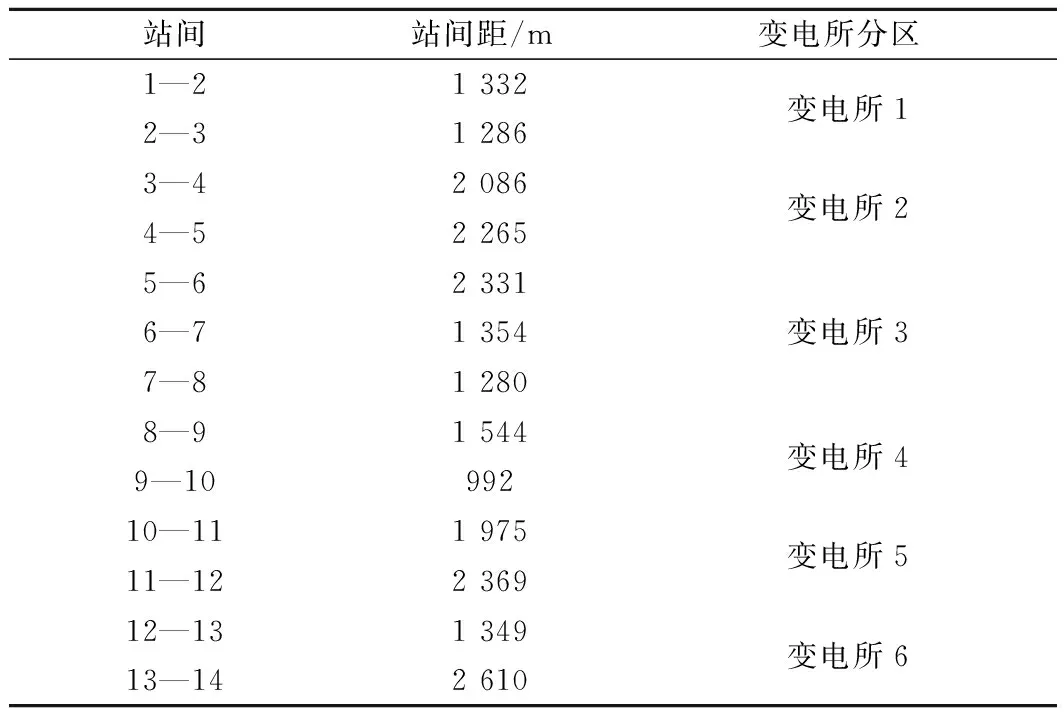
表5 北京地铁某线路数据

表6 北京地铁某线路现行停站方案
4.1 仿真验证
首先,本文模型在计算再生制动能量时考虑了列车牵引制动重叠时间的分布和列车前后距离的影响,为体现其与不考虑影响因素的计算方法相比拥有更高的精准度,以高峰小时为例将本文计算方法结果、不考虑影响因素的计算方法结果与软件仿真结果进行了对比,利用4.2节高峰小时案例分析中的参数和数据进行计算,对比结果见图8。图中可以看出本文考虑多种影响因素的计算方法相比不考虑影响因素的计算方法更贴近于仿真软件得到的仿真结果,尤其是在利用再生制动能量更大的发车间隔时,本文的计算方法有着明显更高的契合度。本文计算方法结果与软件仿真结果的相关系数达到了0.965,该方法拥有足够的精准度并可用于实际案例进行分析。
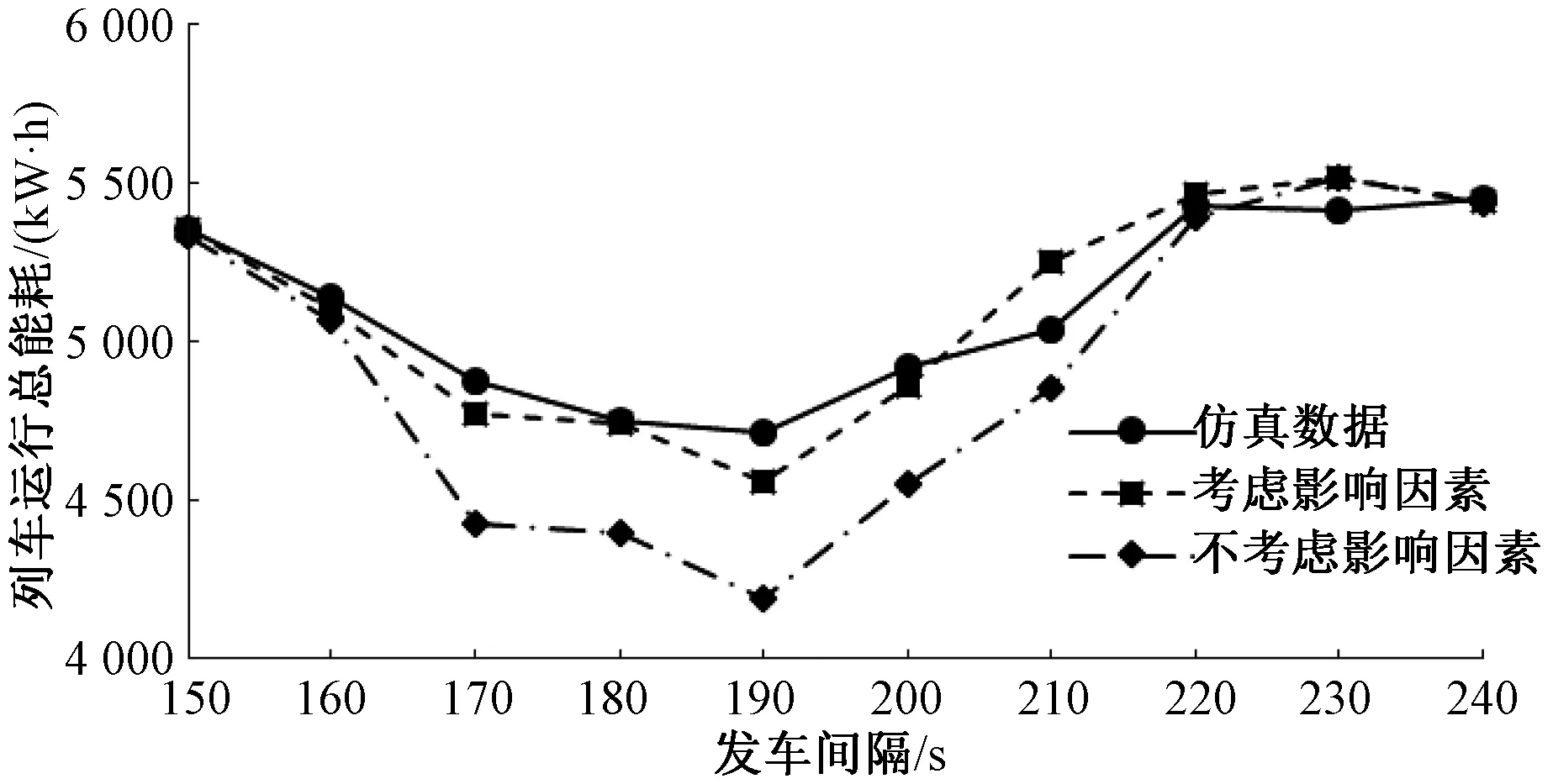
图8 高峰小时不同计算方法计算结果对比图
4.2 高峰小时案例分析
根据北京地铁某线路的实际运行时刻表及客流数据,将高峰小时的发车间隔定为150~240 s,平均1 h发车数量为20辆。在高峰小时的案例中,设车辆数I为20,交叉概率为ppc为0.6,变异概率ppm为0.5。通过计算得到最优的列车停站方案见表7,发车间隔为191 s,最小列车运行净能耗为4 524.711 3 kW·h,根据实际运行时刻表计算所得净能耗为4 776.726 7 kW·h,能耗降低5.28%。
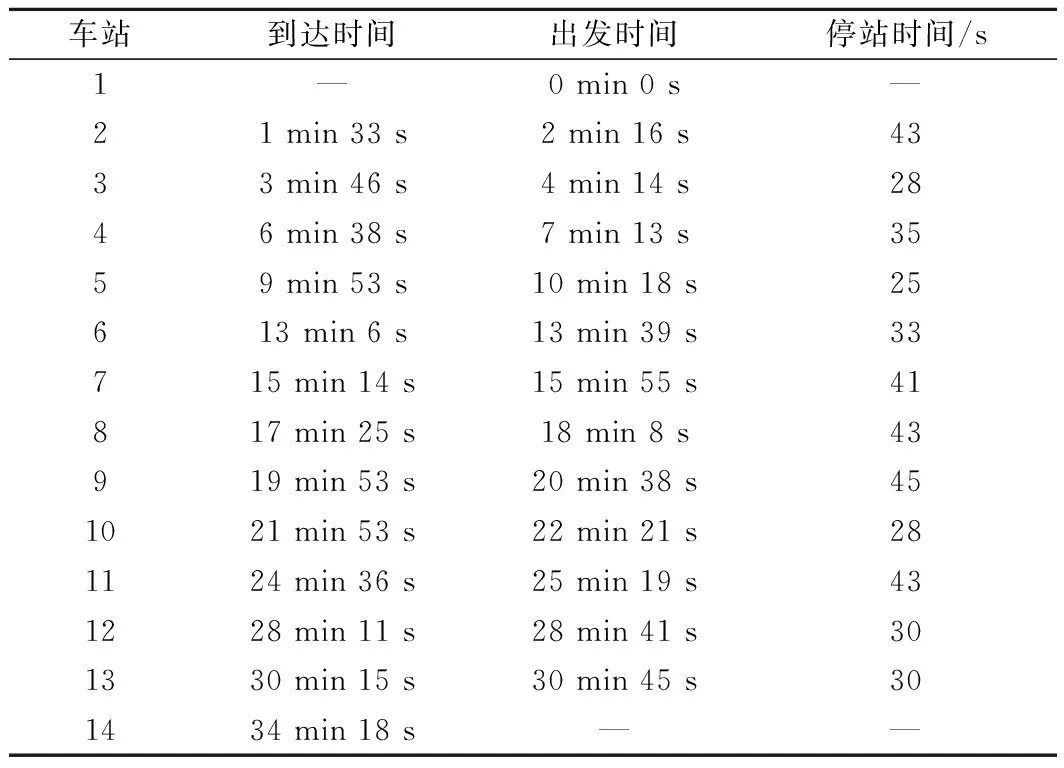
表7 高峰小时优化后停站方案
为体现本文模型与算法通过优化停站时间来利用更大的再生制动能量的效果,设计实验将发车间隔设为从150 s递增至240 s的定量,得到了图9所示的对比图,从图中可以明显看出在不同的发车间隔条件下,优化后的时刻表相比现行时刻表普遍有着更低的总能耗。当发车间隔处于150 s和230 s的时候,两种时刻表的列车能耗是相同的,说明此发车间隔下只存在处于同一区间内的前后车之间的再生制动能量利用,停站时间调整无法影响此种情况,而在160 s至220 s,优化后的时刻表较现行时刻表有着明显的优化效率。
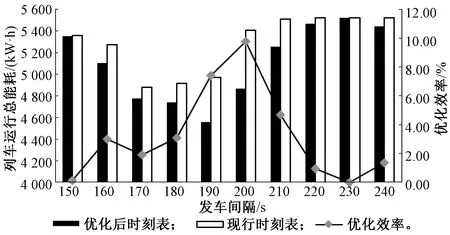
图9 高峰小时列车运行总能耗对比图
4.3 平峰小时案例分析
平峰小时的发车间隔为240~360 s,平均1 h发车数量为12辆。所以,在平峰小时的案例中,设车辆数I为12,交叉概率为ppc为0.6,变异概率ppm为0.5。通过计算得到最优的列车停站方案如表8所示,发车间隔为307 s,最小列车运行净能耗为2 900.520 5 kW·h,根据实际运行时刻表计算所得净能耗为3 066.635 kW·h,能耗降低5.42%。

表8 平峰小时优化后停站方案
与高峰小时案例同样,设计实验将发车间隔设为从240 s递增至360 s的定量,得到对比图,见图10,从图中可以明显看出在不同的发车间隔条件下,优化后的时刻表较现行时刻表也同高峰小时案例一样有着更好的优化效率,验证了本文所提优化模型可以同时适用于高峰时段和平峰时段。
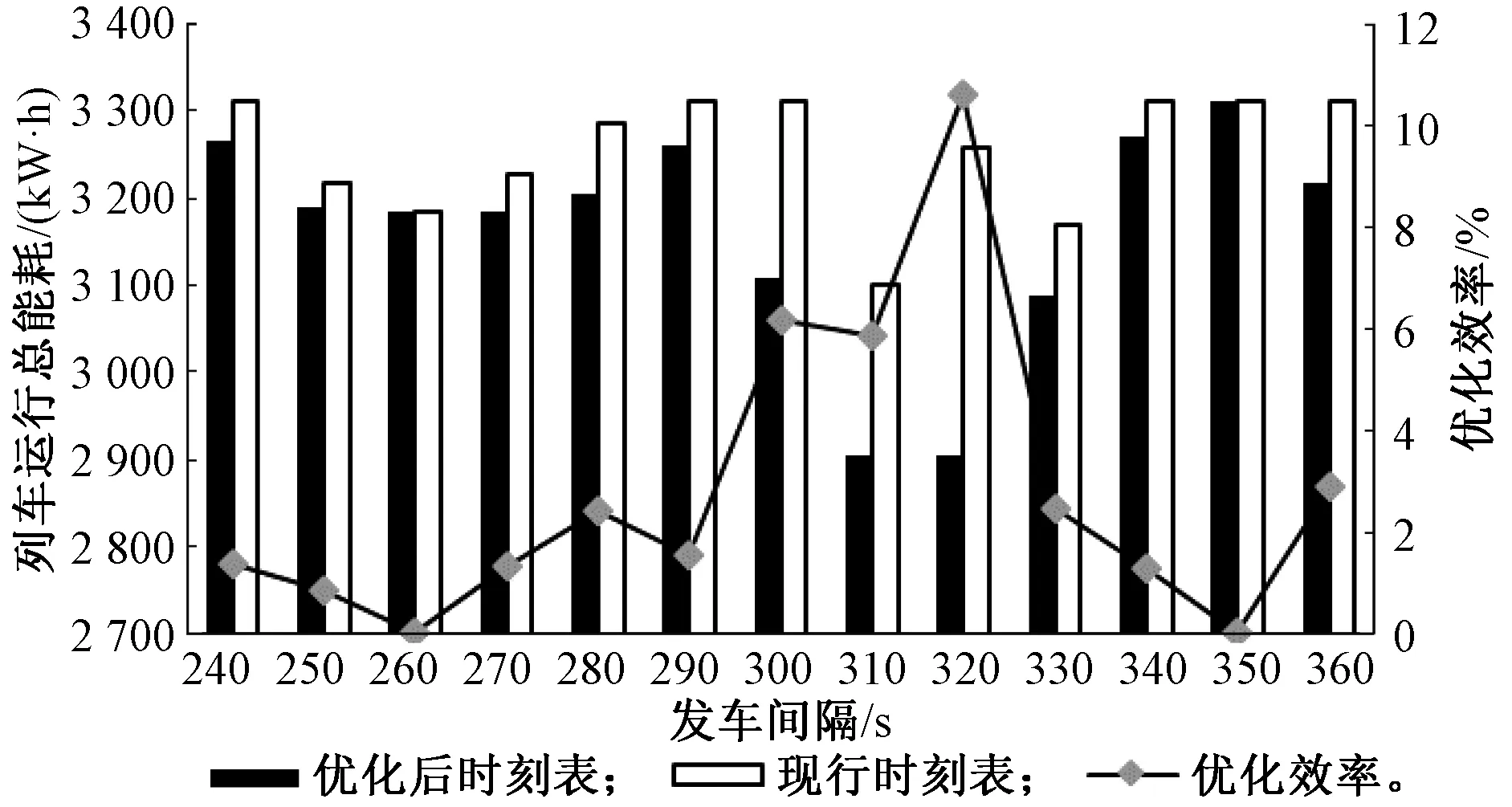
图10 平峰小时列车运行总能耗对比图
5 结 论
本文深入分析了前后车牵引制动重叠时间以及前后车距离对再生制动能量利用率的影响,建立了基于再生制动能量利用的列车时刻表优化模型,并设计遗传算法进行求解。通过算例分析,首先验证了本文考虑多因素的再生制动能量利用方法的准确性,并将该方法应用于北京地铁某线路,与现行列车开行方案进行了对比,结果表明:本文建立的列车时刻表优化模型具有良好的优化效率,高峰时段和平峰时段均可提高节能效果。
