单元视域下的公式研究型教学——以“两角差的余弦公式”为例

黄仙萍

(浙江省台州市黄岩中学，318020)

数学公式课很重要,但现实教学中存在一些问题,导致公式教学不能发挥应有的教学价值．本文以“两角差的余弦公式”为载体,说明如何在单元视域下进行公式的研究型教学，让学生在研究的过程中知道公式的生长点和根、公式的通路和网络,掌握研究数学问题的一般方法，感悟其蕴含的思想方法,明晰公式研究的必要性、公式的整体性、联系性和发展性,完善知识结构和认知结构.

一、问题的提出

数学公式反映了数学对象属性之间的关系,它是对数学对象(关系)的具体表征．数学公式(定理、原理等)课是一个重要课型,对思维训练、素养培养起着重要的作用,它的教学价值不仅仅是促进知识技能的掌握,更在于促进学生的数学理解、数学迁移、数学探究、数学创新能力的发展．但是,在日常教学中有时出现压缩公式的研究、生成过程,轻过程重应用,将公式课演变成习题课．这样会导致学生对公式的理解浮在表面,容易遗忘公式,更别说体悟公式的背景和内涵．希尔伯特指出:“一个数学概念、方法或事实彻底被理解了,是指它和现有的网络有更强或更多的联系连结着”．因此，在单元视域下进行公式的研究型教学,让学生在研究的过程中知道公式的生长点和根、公式的通路和网络,掌握研究数学问题的一般方法、感悟其中蕴含的思想方法,明晰公式研究的必要性、公式的整体性、联系性和发展性,完善知识结构和认知结构,在深度学习中发展核心素养.

从内容上看,两角差的余弦公式是三角恒等变换继诱导公式、平方关系式后的又一个变换公式,可以理解为这两个公式的一般形式,同时又是后续两角和差的正、余弦公式推导的基础;从推导方法上看,两角差的余弦公式与前述公式的推导方法完全一致,都是通过两次运算形成(单位圆终边上的点P用三角函数表示、对称性用代数式表示);从研究方法上看,公式的研究操作性强,在研究型教学模式指导下，学生更易形成适合自己的研究路径,更能培养学生的创新能力．在单元视域下进行设计两角差的余弦公式,学生能更好地理解三角函数是刻画圆周运动的数学模型，三角函数就是圆函数.

二、单元视域下两角差的余弦公式案例

1.创设背景,提出问题

前面我们研究了三角函数,研究了三角函数定义、公式、图象与性质．会用诱导公式与平方和关系式进行化简、求值、证明,也就是进行三角恒等变换．那么，在三角恒等变换过程中，除了诱导公式、平方和关系式,还需要其它公式吗?

问题某城市的电视发射塔建在市郊的一座小山上．如图1,小山高BC,在地平面上有一点A,测得点A，C间距离为60米,从点A测得视角∠CAD=45°,∠CAB=15°,求这座电视发射塔的高度.

设计意图回顾前面研究函数的基本内容,三角恒等变换和解决问题都有必要探究其它公式,从数学内部的发展和现实问题解决的需要提出研究公式的必要性.

预设:AB=60cos 15°,DB=60cos 15°·tan 60°,BC=60sin 15°,DC=DB-BC.

师:如何计算cos 15°与sin 15°?

预设:只需计算其中一个就够了,再利用平方和关系式求另一个．cos 15°=cos(45°-30°),cos 15°=cos(60°-45°).

师:将其一般化，就是求cos(α-β).是否有cos(α-β)=cosα-cosβ?

cos(α-β)与cosα,cosβ有什么关系?这节课我们就来研究两角差的余弦公式.

设计意图该问题本质上就是求出两角差的余弦公式．数学发现大多数是先猜想再证明,在教学时也应该让学生经历这种思维过程．数学猜想并不是凭空乱猜,而是基于一定的知识与方法进行猜测,那种没有思维含量的凭空猜想必须摒弃.

2.联想激活,寻求方法

师:前面有没有学过类似的两个角的差的余弦公式呢?

师:如果把特殊角变成一般的角,诱导公式就变成任意两角和、差的式子.

问题1你能回顾一下诱导公式的推导过程吗?

设计意图联系研究过的知识与方法,发现两角差的余弦其实就是特殊角与角α的差的余弦的一般形式,既然是特殊与一般关系,那么研究方法应该存在一定的联系．这样让知识、方法以整体性的面貌呈现给学生.

预设:诱导公式的推导是通过两次运算,一次运算是点的坐标用三角函数来表示,二次运算是运用圆的对称性给出对称点的坐标关系.

3. 提出猜想,证明猜想

问题2当角α,β确定时,cos(α-β)的值确定吗?为什么?

预设:当角α,β确定时,α-β确定,因此cos(α-β)的值也确定.

问题3你能猜想cos(α-β)与α,β的哪些三角函数值有关呢?你是怎么猜想的?

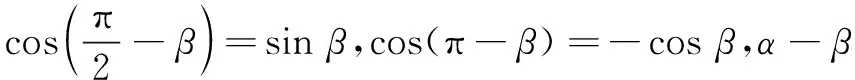
问题4你能计算cos 15°吗?你是怎么想到的?你能将cos(45°-30°)一般化，猜想cos(α-β)与α,β的三角函数的关系吗?

预设:画单位圆表示15°,转化成15°=45°-30°，或者15°=60°-45°,15°在单位圆中的位置不同,转化到始边确定的位置．cos(45°-30°)=cos 45°cos 30°+sin 45°sin 30°，猜想:

cos(α-β)=cosαcosβ+sinαsinβ.

设计意图猜想虽然是猜,但是猜想往往是基于数与形、已知的知识与方法、定性与定量的结合．猜想之前应先作可行性分析,两角差的余弦公式是否存在,如果存在,与什么有关,最后才是什么关系．要寻找什么关系，可以从特殊到一般,从诱导公式这种熟悉的形式猜与谁有关,从特殊角的计算猜存在什么关系．至于如何计算,还是回到最根本的三角函数定义及三角函数是圆函数．毕竟数学命题是基于数学概念之间关系的判断,它是数学概念的一种表现形式.

问题5你能探究cos(α-β)与α,β的三角函数的关系吗?

教师边演示几何画板边提问．如何变化角α-β，α，β的终边?是三个角的终边都变化呢？还是固定一个角的终边,变化另两个角的终边呢?固定哪个角的终边,其它角的终边变化中有什么不变呢?

设计意图猜想不一定可靠,因此离不开演绎推理．既然发现了两角差的余弦与这两个角的正弦、余弦都有关系,就可以回到最根本的定义上进行探究．这里就涉及到三个变量函数值的关系的探讨,多变量函数关系的研究通常是固其它动一,这里动一必有动二,就转变成固一动二了,因此问题就转化为分析动谁导致谁在变化．这本质上是两个圆周运动来刻画圆周运动的叠加,让学生从本质上认识到这与前面单位圆上质点作圆周运动得到的公式是整体一致的.

[1-cos(α-β)]2+sin2(α-β)=(cosβ-cosα)2+(sinα-sinβ)2.

化简得cos(α-β)=cosαcosβ+sinαsinβ.

方法二向量法(由特殊法发现两角差的余弦公式的特点与向量的数量积公式很接近,因此用向量法推导)

如图2,在直角坐标系,以Ox轴为始边分别作角α,β,其终边分别与单位圆交于P(cosβ,sinβ),Q(cosα,sinα)两点,利用向量的数量积运算得到:

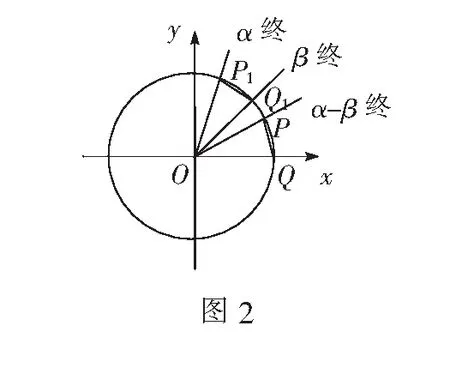
cos(α-β)=cosαcosβ+sinαsinβ.

向量的夹角θ=α-β+2kπ或者θ=β-α+2kπ,因此,

cosθ=cos(α-β)=cosαcosβ+sinαsinβ.

问题6两角差的余弦公式与平方和关系式sin2α+cos2α=1有什么关系?

预设:当α=β时,cos 0=cosαcosα+sinαsinα，即sin2α+cos2α=1.

4. 巩固运用,深化理解

例1证明:(1)cos(π-α)=-cosα;

设计意图一方面对新学公式进行运用,使得学生更好地记忆公式;另一方面通过练习,让学生再一次体会到诱导公式是两角差余弦公式的特殊形式,加深学生对公式整体性的认识.

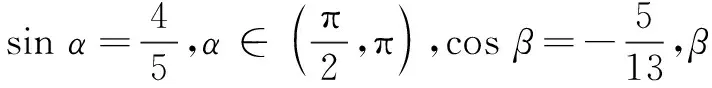
设计意图对公式的熟练运用是低阶思维,通过学生自主编题，明白公式的本质与代换思想,使低阶思维变成高阶思维.

5.回顾反思,内化迁移

(1)这节课我们学了什么公式?你能说说公式的研究过程及研究思路吗?

(2)对公式的应用,你有哪些经验与体验?

(3)圆对称性(特殊)的代数形式是诱导公式,而圆的对称轴有无穷多条,比如直线y=tanα·x是圆对称轴更一般的形式,由此对称轴你能推导得到更一般的诱导公式吗?它是怎样的?

(4)三角恒等变换包括名称的变换与角的变换,你能将两角差的余弦公式从这两个角度进行变换,探究得到一些新的公式吗?

设计意图(1)对知识、方法作一个回顾;(2)对思想、活动经验作一个反思;(3)让学生在单元视域下再从形的角度去猜测特殊性与一般性;(4)新公式的学习不仅要跟过去的公式建立整体联系,也要为后续公式的学习做好铺垫,对研究问题进行展望.