基于强化学习的快速探索随机树特殊环境中路径重规划算法

邹启杰 ，刘世慧，张 跃，侯英鹂

(1.大连大学信息工程学院，辽宁大连 116000;2.国防科技国家创新研究所无人系统研究中心，湖南长沙 410000)

1 引言

移动机器人成功应用到工业、医疗、娱乐和军事等领域的前提是其能够安全自主地行进.路径规划是决定移动机器人如何在多约束条件下主动避障并安全达到目标位置的核心技术，也是其他机载任务的执行前提，可见路径规划是核心性基础研究;同时，移动机器人作业环境的多样性和未知性、以及实时性约束，又给规划问题带来极大的挑战性.因此路径规划具有重要的研究意义.根据环境信息是否完全已知，可将移动机器人路径规划分为:1)全局路径规划，又称离线路径规划;2)局部路径重规划，又称在线局部路径规划[1].全局路径规划是已知全局环境信息，在机器人移动前离线规划出一条从起点到终点的运动路径，适用于没有变化的环境，目前全局算法发展相对成熟.但移动机器人的工作环境多数是动态不确定的，部分未知的环境更贴近实际状况.局部路径重规划是移动机器人在环境部分未知的情况下，根据红外摄像机、雷达和激光等传感器获得的当前环境信息，规划出一条从当前路节点到下一个路节点的最优无碰撞路径，且满足实时性.

目前常用的局部路径重规划方法主要有人工势场法、栅格法、滚动窗口法和采样搜索方法等，结合遗传算法、蚁群算法、模糊逻辑算法、人工智能和神经网络[2]等智能搜索算法，以提高搜索效率，系统鲁棒性以及适应能力.但是这些典型算法多数针对已知环境模型进行搜索，对于部分未知环境会耗费时间搭建精准的环境模型;当障碍物与目标距离较近时，产生的合力或者智能搜索方法的规则设置不合理都有可能导致机器人无法到达目标;此外规划出的路径可能充满拐点，导致机器人频繁调整行进方向，影响舒适性和行进效率;或算法计算时间维数爆炸，不具有收敛性.尤其是针对一些特殊环境，如U型、狭窄且不规则的环境中，性能无法保证，甚至威胁机器人自身安全.总之，要求计算速度要快，安全性要高，是一个有挑战，也有重要意义的工作.

与以上算法相比，1998年提出的快速扩展随机树(rapidly-exploring random tree，RRT)[3-4]算法兼顾规划效率和效果，是一种随机采样式树结构算法，解决高维位姿空间和非完整性约束下的路径规划问题.为提高随机采样效率，LaValle等[5]提出了双树结构的RRT-Connect算法，分别从初始点和目标点建立随机树，算法具有收敛性和概率完整性，但依然没有改变随机性.为增强RRT扩展树的目标趋向性，徐娜等[6]将目标偏向思想引入到RRT中.Karaman S等[7]提出RRT*算法，以在线方式进行运动规划，具有渐近收敛到全局最优解的优点，但由于计算慢，导致实时性较差.Sohn K等[8]提出用RRT算法规划初始次优运动，然后使用Q--Learning算法以优化能量消耗的轨迹，因而输出的是全局规划的优化轨迹.Pareekutty N等[9]提出了RRT-HX算法，使用强化学习对RRT生成的轨迹进行评估，采用质量偏差的成本信息来识别低成本路径，但没有从本质上降低RRT采样的随机性.针对大规模的障碍物密集环境，Alejandro等[10]提出了quad-RRT算法，通过四棵树扩展平衡搜索能力与连接初始和目标路径两侧的并行探索，却没有考虑实际机器人的运动学模型.Kun Wei等[11]提出S-RRT算法，在动态非结构化环境中，采用定向节点的方法扩展，进行最大曲率约束以及轨迹优化，提升效率，但遇到未知的障碍物会停止运行，因此只能用于进行全局规划.为改善路径质量，Cao等[12]使用遗传算法优化RRT算法生成路径，但由于环境信息是固定的，导致规划实时性较差.

与上述算法对环境适应性较差不同，在利用强化学习[13]解决路径规划问题方面，Faust等[14]提出利用偏好评估的强化学习，提高智能体学习效率，在复杂的环境下使得移动机器人快速得到无碰撞路径;Shalev-Shwartz等[15]将深度强化学习方法融合策略梯度法，用于解决未知环境中无人车的路径规划问题;Kulkarni等[16]采用目标驱动内在动机的深度强化学习方法，在反馈稀疏的环境中学习目标导向行为，提高机器人在复杂环境中的规划速度.研究表明，强化学习方法不仅能够有效地弥补前几种局部规划算法方法所存在的不足，还能够提高移动机器人在部分未知环境中的自适应性和自学习能力.

目前移动机器人的局部路径重规划技术领域取得了可喜的进展，但在高可靠性、高适应性、自主性方面仍存在着许多的不足，本文采用快速扩展随机树(RRT)与强化学习Sarsa(λ)算法相结合，解决特殊环境下机器人局部路径重规划问题.特殊环境是指包括狭窄通道、障碍物密集、有凹型等受限的空间环境，总体来说就是机器人易陷入连续低效规划的区域.实验结果表明，本文提出的算法能够全面提升机器人特殊环境下局部重规划的性能，即减少计算时间，具有较强实时性;节省机器人能源;提供合适的位姿角度变化，提高路径规划稳定性;并且在部分未知环境和特殊环境具有良好适应性和安全性.

论文的第2部分介绍了原始算法;第3部分，详细描述基于强化学习(reinforcement learning，RL)驱动快速探索随机树(RRT)的局部路径重规划方法(RL-RRT);第4部分，通过MATLAB和机器人操作系统(robot operating system，ROS)软件平台进行实验仿真，对算法进行全面的性能测试和仿真结果分析;文章最后，总结本文贡献，并说明后期其他相关工作.

2 基本算法描述

RRT算法是一种典型的基于随机性搜索的路径规划算法，该算法通过3个步骤:构建树、探索树和确定解节点，最终形成规划路径.

RRT算法首先将初始节点xinit作为快速随机搜索树T的根节点，然后在可行空间中随机选取一个状态点xrand，遍历当前的快速随机搜索树T，当找到T上距离最近的节点xnear，经过一个控制周期到达新的状态节点xnew，将新状态节点添加到快速随机搜索树T中，通过随机采样增加叶子节点的方式，不断扩展随机树，最后当随机树中的叶子节点包含了目标点或进入了目标区域，反向追溯到根节点便可以在随机树中找到一条由从初始点到目标点的路径，随机树构建结束，如图1所示.

图1 RRT算法节点扩展示意图Fig.1 RRT algorithm node expansion diagram

由于RRT算法本质是随机采样扩展，当处于特殊环境，比如初始点和目标点之间有较多障碍物时，大量的随机点会落在障碍物周围，如图2所示，扩展树在无效区域探索，难穿越障碍物区域，导致无法快速到达目标点.

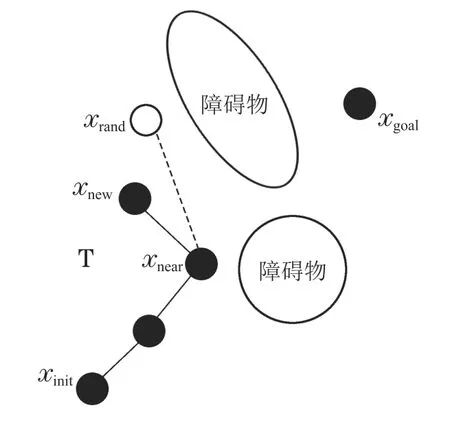
图2 RRT特殊环境节点扩展示意图Fig.2 RRT node expansion diagram under the peculiar environment

简言之，传统的RRT算法应用到移动机器人特殊环境，如障碍物密集且不规则、凹型等环境，路径规划中存在以下问题:

1)目标性弱，探索无效区域耗费代价较大.由于算法路径规划的随机性，随机采样点均匀分布在全局空间，导致搜索空间中有过多的冗余搜索，表现为搜索树均匀布满空旷环境空间;

2)狭窄通道花费时间长.由于窄道、凹角通道面积相对较小，均匀随机采样点搜索到通道的概率低，导致机器人在狭窄通道会花费大量的时间探索却一直无法通过;

3)拐角多、旋转角度不可行.搜索出来的路径曲率变化过大，甚至出现小范围内直角变化，这样的路径并不能满足机器人的运动学模型，无法直接应用于移动机器人;

4)实时性能较差.离线全局搜索构建随机树，一次性规划路径，使算法通常只能应用在已知环境中，实时应用性较差.

3 RL-RRT算法

3.1 基于POMDP机器人路径规划模型

面对部分未知环境，移动机器人不一定知道所处环境中的所有确定性信息，因此不能为当前位置状态提供确定性动作，因而移动机器人需要局部重规划.考虑到移动机器人局部重规划存在的不确定性，并不能观测到所有状态，因此本文将机器人路径规划问题定义为部分可观察的马尔科夫决策过程(partially observable Markov decision process，POMDP)七元组，LP＜S，A，Ω，P，O，R，γ ＞描述如下:

1)S状态.

通过分析传感器感应状态，将局部路径重规划POMDP模型状态空间指定为移动机器人的具体位置，用S={s0，s1，s2，···，sn}表示，其中:在世界坐标系Xworld－Yworld下用si(xi，yi，θi)(i ∈(0，n))表示局部路径重规划中移动机器人的位置.

2)A动作空间.

A表示移动机器人的可行动作，在移动机器人速度不变化的情况下，机器人采取的动作是根据当前状态向下一个状态转移的旋转角度和障碍物位置确定，具体动作方向空间定义为A={a1，a2，a3，a4}，其中各动作代表机器人移动方向.

3)ΩA观察空间.

ΩA是一组观察结果集ΩA={ΩO，Ωfree}，观察值表示环境中障碍物分布情况，如果观察位置有障碍物则观察结果统一表示为ΩO，无障碍物的空白位置则可表示为Ωfree.

4)P :S×A →S状态转移概率矩阵.

由于在当前状态下执行指定动作后，下一时刻状态无法完全确定，这种状态转移不确定性可以使用状态转移概率矩阵描述，P是n×n维状态转移矩阵，Pa(s′|s)=P(s′|s，a)表示移动机器人在时间t状态s采取动作a可以在时间t+1转换到状态s′的概率.

5)O观察值转移函数.

观察值通过障碍物的位置确定，同样传感器障碍物检测也可能由于传感器失灵因素导致输出错误结果或观察不完全，O是n×m维条件观察概率矩阵，观察值作概率性定义:Oa(Ω|s)表示机器人在执行动作a转移到状态s观察到Ω的概率.

6)R:S×A →R回报函数，R(s，a)表示机器人在状态s执行动作a带来的环境回报.

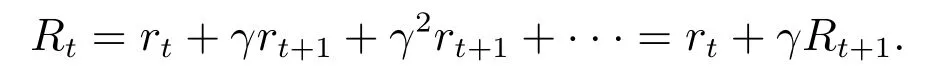
7)γ是折扣因子，γ ∈[0，1]反映了移动机器人对未来动作的重视程度，γ越大，近期回报影响越小，使得长期回报更有意义，一般文献中γ 的取值大多在0.9～0.98之间[17-18].

3.2 RL-RRT算法基本步骤

由于原始RRT算法探索方向具有随机性，并且扩展点的选择依赖于距离函数的设计，不能很好地满足局部重规划的实时性和复杂性.本文提出的RL-RRT算法是一种基于强化学习Sarsa(λ)构建RRT树型搜索的规划算法，引入强化学习在交互过程中提升扩展点选择的时效性，在RRT的节点扩展过程中采用强化学习趋向目标搜索避障策略，即目标区域对树的扩展产生正向奖励，同样障碍物和环境边界对树的扩展起到负向抑制作用.力求降低RRT算法盲目性，提升未知特殊环境下的规划安全性、实时性和高效性等性能.

RL-RRT算法的流程图如图3所示，虚线包含部分基于Sarsa(λ)的扩展点选择过程.

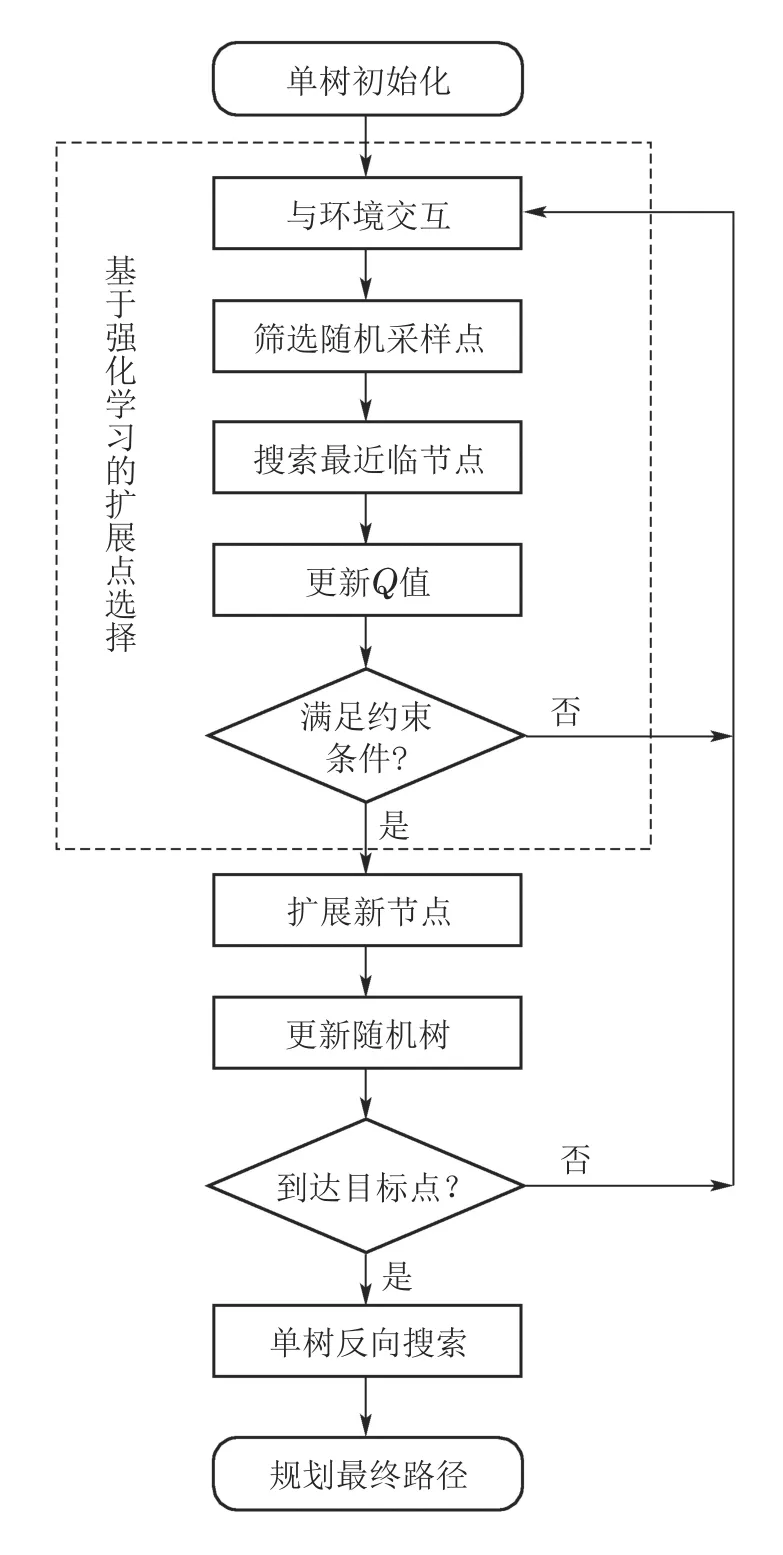
图3 RL-RRT算法流程图Fig.3 Flow chart of RL-RRT algorithm

选择时间差分方法的原因不仅在于其可以容易地扩展到大的状态空间，并且也不同于蒙特卡罗方法需要等到实验结束才能更新模型，更适合于局部重规划的实时性要求.时间差分方法包括Sarsa与Q--Learning，两者不同之处在于值函数的更新方式.Sarsa算法比Q--Learning 具有更强的鲁棒性，更能满足机器人实时性和安全性约束[19].若环境信息全部先验已知，则可以通过确定性的运动规划方法获得最优解.然而针对POMDP问题，在无法获得所有环境信息情况下，使用Sarsa算法能将当前具有最小代价边所经过的节点按顺序连接起来作为最终的规划路径，快速收敛.此外，Sarsa的动作选择相对保守，学习迂回策略会选择先远离危险区域，再追求到达目标点，更符合移动机器人路径规划的安全性需求[20-23].最后，Sarsa(λ)算法比Sarsa算法更能体现出移动机器人在路径规划时，一系列位置变化对于到达目标点所做出的贡献，提高移动机器人的学习效率，加快收敛速度，更适合于局部重规划的高效性要求.

移动机器人主动避障是通过路径规划绕开障碍物或危险的路径，实现安全行驶.然而原始RRT算法路径规划时，存在靠近障碍物时无法及时避障的问题，对移动机器人来说很危险，特别是某些领域需要机器人完全非碰撞且舒适地抵达目的地，如医疗、助老等领域对安全性有很高的要求，如果造成碰撞会产生严重后果.如图4所示，RRT算法的部分路径非常接近障碍物，甚至部分轻微进入障碍物区域(蓝色矩形圈出的区域).

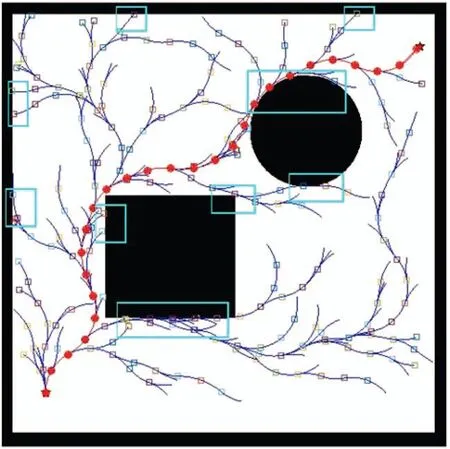
图4 RRT算法仿真结果Fig.4 RRT algorithm simulation result

针对一般宽通道，结构化区域，机器人规划成功，而对于窄道、凹角等特殊环境性能下降，对于实时性、安全性、舒适性有要求的机器人该问题更突出，如物流机器人、交通拥堵下的智能车辆.基于移动机器人行走安全性考虑，本文对障碍物采用图像的形态学运算膨胀操作.障碍物膨胀区域是按照机器人的实际半径尺寸作补偿，即膨胀为真实机器人大小的150%.

3.3 随机节点的筛选

为降低RRT算法的随机性，提高目标趋向性，本文引入偏向目标思想，并对随机节点筛选进行改进.

偏向目标的核心思想是在随机树扩展过程中，通过一定概率使xrand=xgoal，这样扩展树会趋向目标区域延伸，即使在特殊环境，距离障碍物很近，也会提高到达目标点的速率.

随机节点的筛选核心思想是根据R(x)任务回报函数选择随机树的节点.R(x)任务回报函数通过计算每个节点到目标和障碍物的回报值来影响随机节点的选取，根据障碍物的出现与否设置两种不同的权值.R(x)可表示为

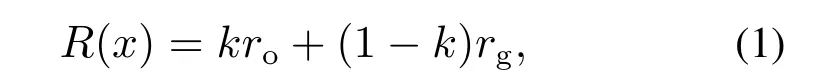
其中:ro为避障动作回报值，rg目标动作回报值，根据环境对节点产生的不同回报值，如式(2)-(3)所示.当优先选择躲避障碍物时k=0.7，而没有障碍物时k=0.k ∈{0，0.3，0.7，1}是人为设置的动作回报函数的权值，k值选取依据见本文第4.1.2节.

根据移动机器人与障碍物之间的距离不同，移动机器人状态分为3种:“安全”、“避碰”、“碰撞”，如图5所示.其中xt表示当前节点位置，考虑到实际机器人左右两侧车轮的间距为L，设d1与d2间距离为L，如式(4)表示.

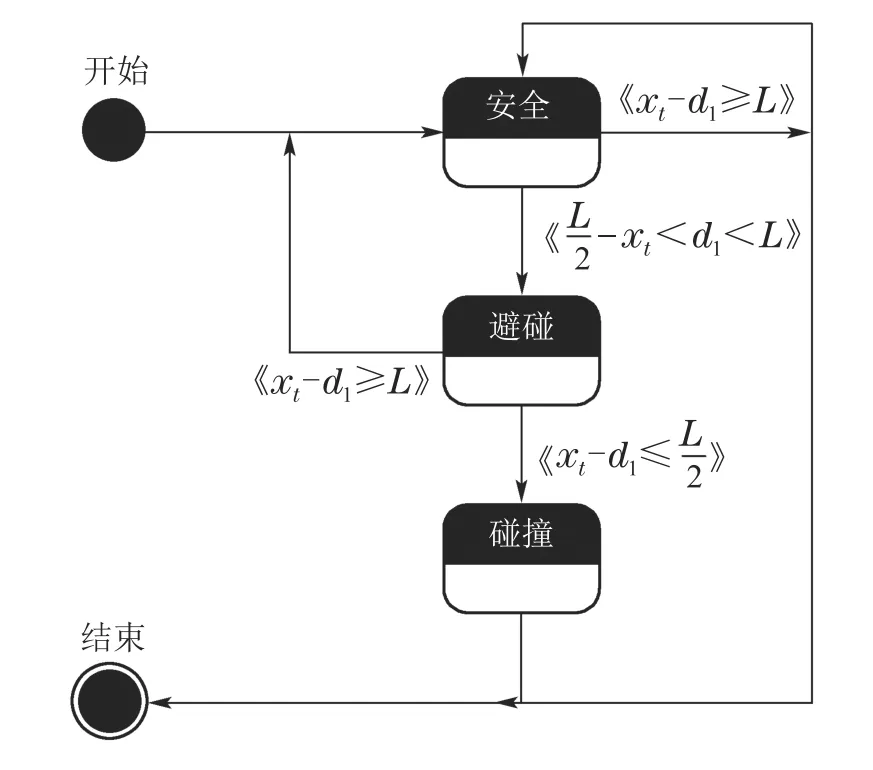
图5 移动机器人状态图Fig.5 Mobile robot state diagram

3.4 扩展树

原始RRT树在空间中是随机均匀扩展，因而父节点与子节点相对位置也存在随机性.考虑到机器人前进过程中的稳定性，RL-RRT算法引入路径转角的阈值，它是由3个相邻节点的位置关系加以约束.在扩展树中取3个相邻的节点xnew，xnear，以及xnear的父节点xinit，那么3个节点可构成两个向量，分别为向量，向量，取向量构成的夹角为x，如图6所示.考虑到移动机器人的安全性和舒适性，无法进行大幅度的转向移动，因此将其旋转幅度设置为.

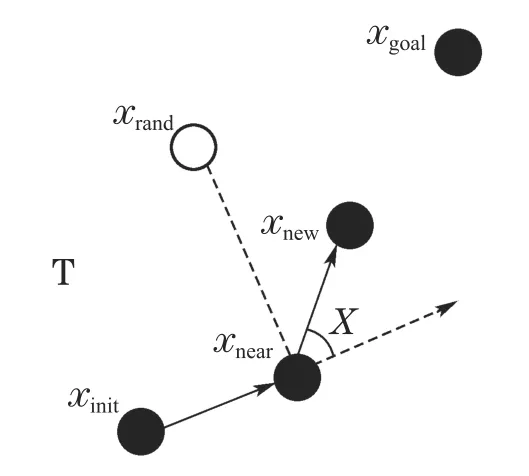
图6 转向角约束Fig.6 Steering angle constraint

为了得到平滑的路径，本文除了对转向角大小进行约束，还通过平滑度目标函数优化路径.当移动机器人寻找最优路径的时候，会发生方向转动，小角度调整机器人的方向会提高其移动效率并节约资源，而大角度调整会使其降低可靠性和舒适性.由此设置大转向角产生低回报，小转向角产生高回报.用|x|代表旋转角度的绝对值，旋转角度的回报可以表示为

将平滑度目标函数Θ(x)作为评价路径平滑的指标，小角度调整移动机器人的旋转角度，使得路径更安全舒适，如式(5)所示:

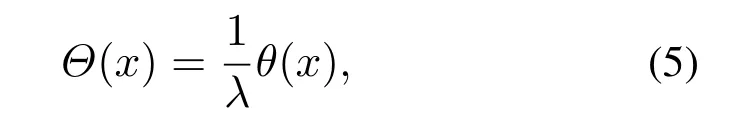
扩展树的节点选择的核心思想是根据E(x)扩展函数，E(x)包含R(x)任务回报函数、L(x)目标距离函数以及平滑度目标函数Θ(x)，可表示为

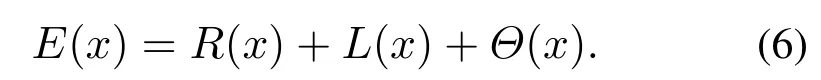
L(x)目标距离函数会通过计算采样点与最近临节点扩展的距离来影响新节点的选取，L(x)可以表示为

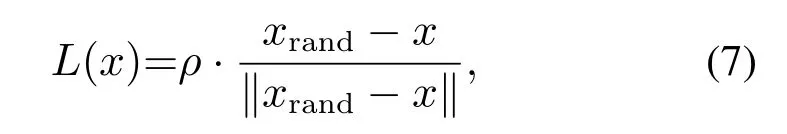
其中:ρ为随机树的步长，xrand表示采样点，x是最近临节点xnear，‖xrand－x‖为欧拉范数定义的两点间距离.

基于障碍物密度的步长分为3种:当环境中的障碍物稀疏时，ρ为ρ1;当环境中的障碍物较密集时，ρ为ρ2;当环境中的障碍物密集时，ρ为ρ3.ρ的大小会影响机器人的速度.

将式(4)-(5)(7)代入式(6)中可以得到

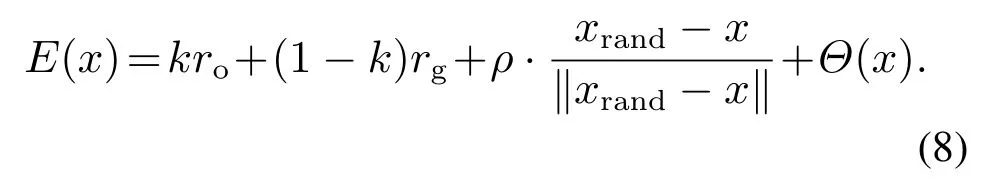
由于式(8)多目标决策评估的值具有不同的量纲(即单位)，因此需要排除量纲的选取对评估结果的影响，本文采用非量纲化和标准0-1进行归一化处理，仅通过数值的大小来反映属性值的优劣，把数值变换到[0，1]区间上，如式(9)-(11)所示:

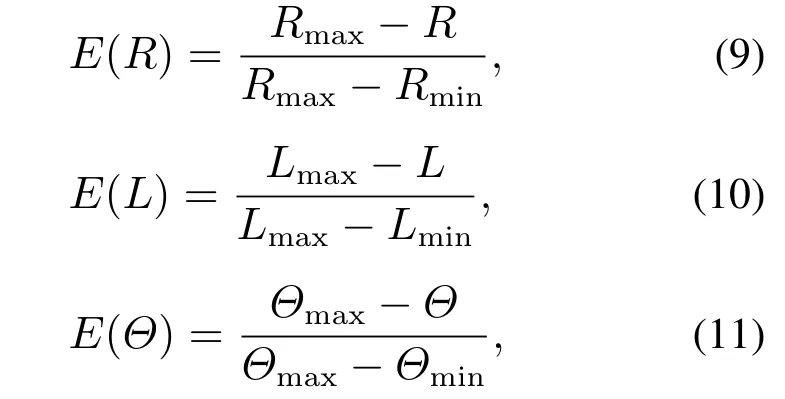
其中:E(R)为任务回报归一化的值，E(L)为目标距离归一化的值，以及E(Θ)为平滑度归一化的值.

为体现出各个目标的优点，本文设置了不同的权值，体现各自的重要性.根据扩展树的权重的设置原则，首先要考虑安全性，其次考虑时间，最后考虑路径的平滑度，即ω1＞ω2＞ω3.根据最小二乘法，设置式如下:

E(x)扩展函数根据式(12)得到新节点xnew的生成表达式如下:

3.5 Q函数的建立

RL-RRT算法通过Sarsa(λ)对扩展树中的每个节点建立学习反馈，不断对环境加深认识.新节点的Q值更新是针对当前节点和后继节点.当环境变化，后继节点的Q值也会发生改变.如果处于可行空间，则产生正向回报，后继节点继续扩展;如果处于障碍物环境，则产生负回报，并且后继节点不会再进行扩展，需要重新选择新的安全动作，依此类推，直到下一状态为非障碍物状态.与原始RRT算法的节点随机扩展分布不同，RL-RRT算法将Sarsa(λ)优化RRT算法主要目标就是将位置状态映射到动作的同时，最大化期望回报，学习避障策略.RL-RRT算法的Q值更新式是

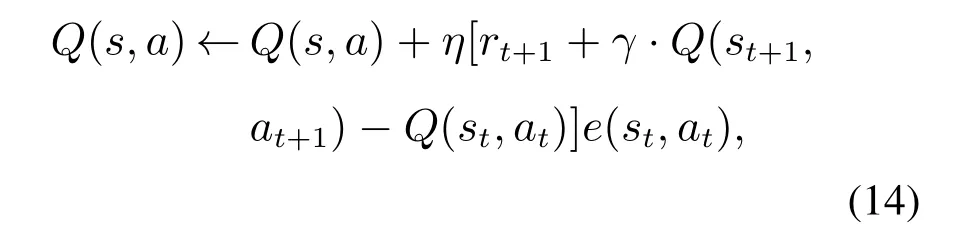
其中:η ＞0是学习率，rt+1表示机器人在t+1时刻采取动作at时获得的瞬时奖励，γ ∈[0，1]是控制机器人前瞻性的折扣因子，e(st)是时间t状态-动作的迹.

rt+1作为瞬时奖励，大小是由式(4)任务回报函数R(x)产生，当机器人到达目标点设置正向奖励回报，与障碍物发生碰撞设置负向奖励回报.

移动机器人从位置st移动到新的位置st+1是基于运动学模型，其位姿信息通过(xR，yR，θR)描述，具体计算见式(15).

e(st)作为状态-动作迹，用于记录移动机器人路径规划过程中对到达目标点做出贡献的访问某一状态的次数.一旦状态被访问，状态-动作迹就增加，反之衰减，反向传播给之前所有的状态，加快收敛速度，直到到达目标点.

Q(s，a)作为动作值函数，利用式(14)进行更新.

4 实验分析

4.1 MATLAB仿真平台

4.1.1 仿真验证

本文使用MATLAB仿真平台，设计5种不同的特殊地图环境.黑色是障碍物区域，白色是可行区域.仿真实验中移动机器人显示为质点，但实验数据设置是考虑到移动机器人大小和环境通道的宽窄.障碍物膨胀区域是按照机器人的实际半径尺寸为标准，即膨胀为真实机器人大小的150%.根据机器人0.35 m的直径大小，狭窄通道宽度设置为0.7 m.障碍物密集的环境是指障碍物占整个环境的较大比例.环境中的障碍物和目标都处于静止状态，并且对于机器人而言障碍物和环境边界是随着行进逐渐感知的.实验对比一方面，将本文提出的路径规划方法与原始RRT算法、双树RRT-Connect算法以及偏向目标GoalBia-RRT算法进行性能对比;另一方面，与未考虑可行旋转角度约束或固定步长的RL-RRT算法对比.

路径规划目标是要在静态二维环境里，为机器人规划一条从起始位置到目标位置的行动路线，要求这条路径满足以下条件:

1)与所有障碍物均保持一定的安全距离;

2)合适的位姿角度变化;

3)路径应尽可能短且平滑.

MATLAB实验有5个不同的特殊地图环境:1)环境1如图7所示，含有弯道的环境，机器人需要从底部出发穿过弯曲通道到达顶部目标点;2)环境2如图8所示，含有一个狭长的狭窄通道，机器人需要从左侧出发穿过狭窄通道到达右侧目标点;3)环境3如图9所示，简单迷宫环境，机器人需要从底部出发穿过3个通道到达顶部目标点;4)环境4如图10所示，内部有凹陷和凸角的障碍物二维环境，机器人需要从右侧底部出发到达左侧顶部，避免陷入凹陷区域无法跳出，到达顶部目标点;5)环境5如图11所示，内部有多个形状不规则的障碍物组成的障碍物密集的二维环境，机器人需要从底部出发穿过多个障碍物，然后到达顶部目标点.

原始RRT算法、双树RRT--Connect算法、偏向目标GoalBia-RRT算法和RL-RRT算法中随机生成树的扩展过程如图7-11所示.

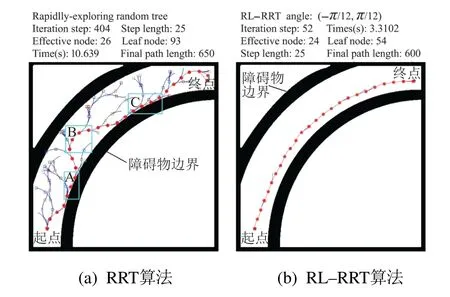
图7 两种算法弯道性能比较Fig.7 Performance comparison of two algorithms in the bend

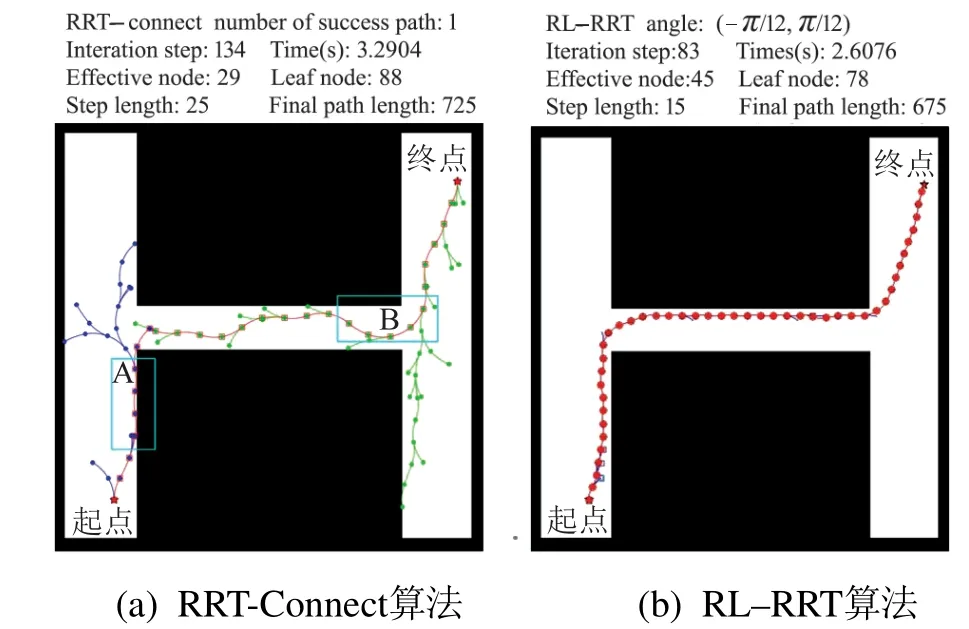
图8 两种算法在狭窄通道性能比较Fig.8 Performance comparison of two algorithms in the narrow channel

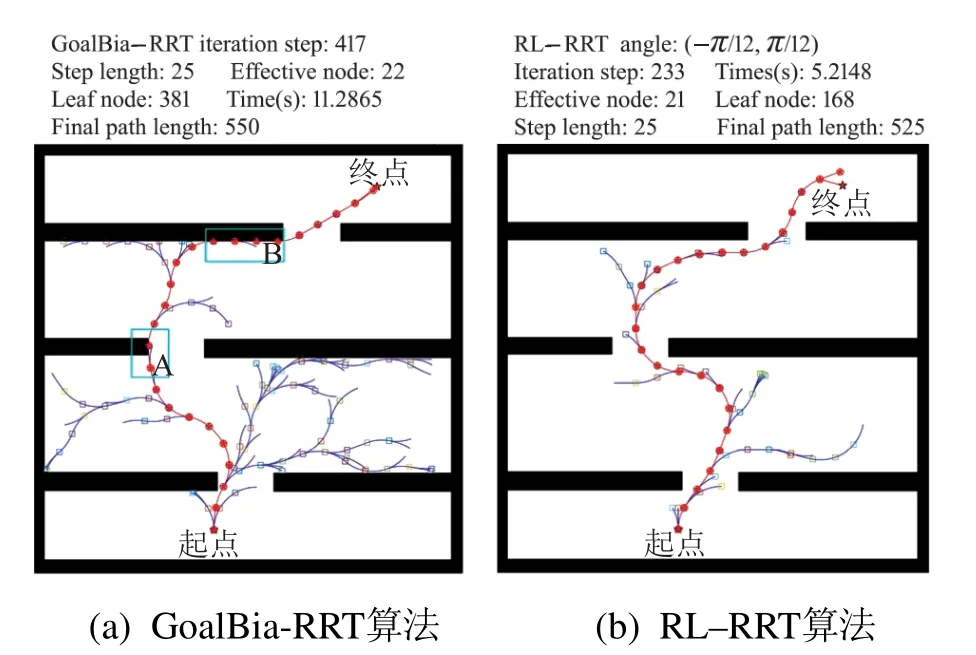
图9 两种算法简单迷宫性能比较Fig.9 Performance comparison of two algorithms in the single maze

图10 RL-RRT算法在凹陷、凸角通道对比是否考虑旋转角度优化Fig.10 RL-RRT algorithm in the concave and convex channel comparison whether consider of rotation angle optimization

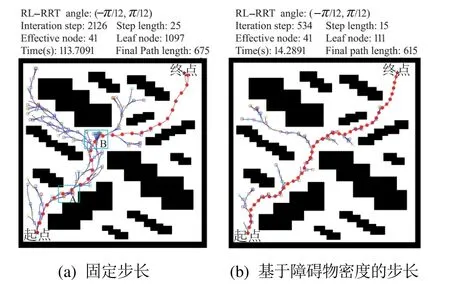
图11 在障碍物密集通道对比不同步长的RL-RRTFig.11 Compare the RL-RRT with the different step length in the dense passage of obstacles

图中深蓝线为从起始位姿节点开始构造的生成树，绿色线为双树结构从目标位姿节点构造的扩展树，红色线为算法规划的从起始位置到目标位置的移动机器人路径轨迹.

从图7(a)可以看出，在弯道环境下，RRT算法效率较低，扩展树均匀分布在空闲区域，缺乏目标性，蓝色矩形A，B和C区域的部分路径非常接近障碍物，甚至小范围内存在明显曲折.从图8(a)可以看出，在狭窄环境下，蓝色矩形A和B区域的部分路径甚至进入障碍物区域，且位姿角度连续波动，RRT-Connect算法安全性和舒适性较低.从图9(a)可以看出，在简单迷宫环境下，蓝色矩形A和B区域的部分路径也非常接近障碍物，虽然目标性较强，但GoalBia-RRT算法依然存在效率低和安全性低的问题.从图10(a)可以看出，在凹陷、凸角通道下，未考虑旋转角度的RL-RRT算法路径曲折，蓝色矩形A区域无障碍物路径角度却变化过大.从图11(a)可以看出，在障碍物密集环境下，固定步长的RL-RRT算法在障碍物密集通道处调整了多次才通过，蓝色矩形A和B区域有明显调整痕迹.从图10(b)和11(b)可以看出，考虑转角和障碍物密度的路径在平滑度和规划效率方面具有明显优势，数据详见表1-2.

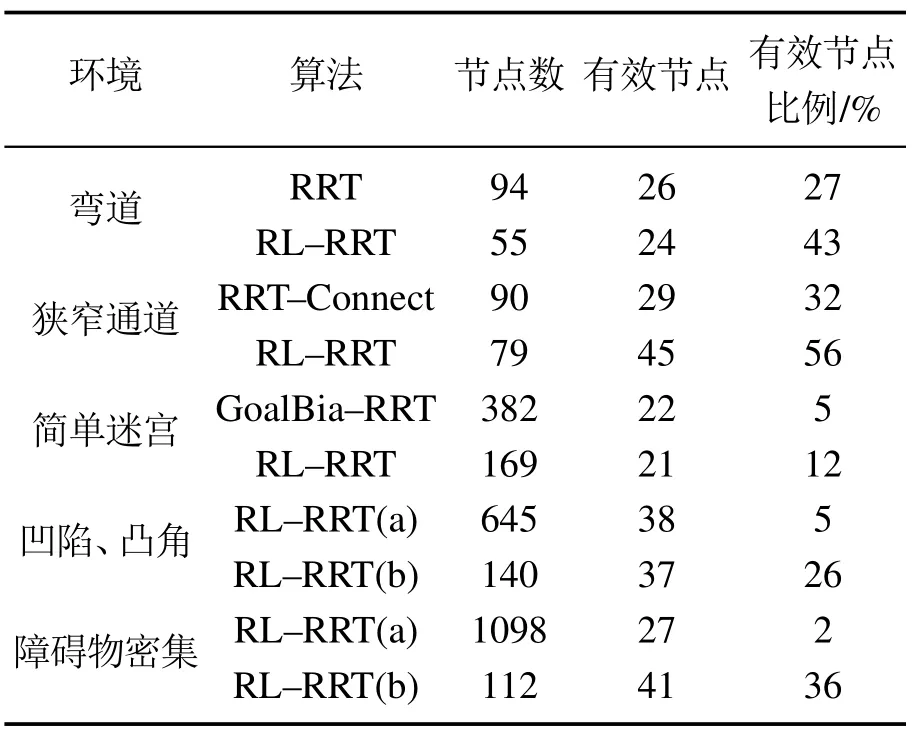
表1 RL-RRT和对比算法在不同环境节点比较图Table 1 Comparison of the nodes number of different environment in RL-RRT and comparison algorithms

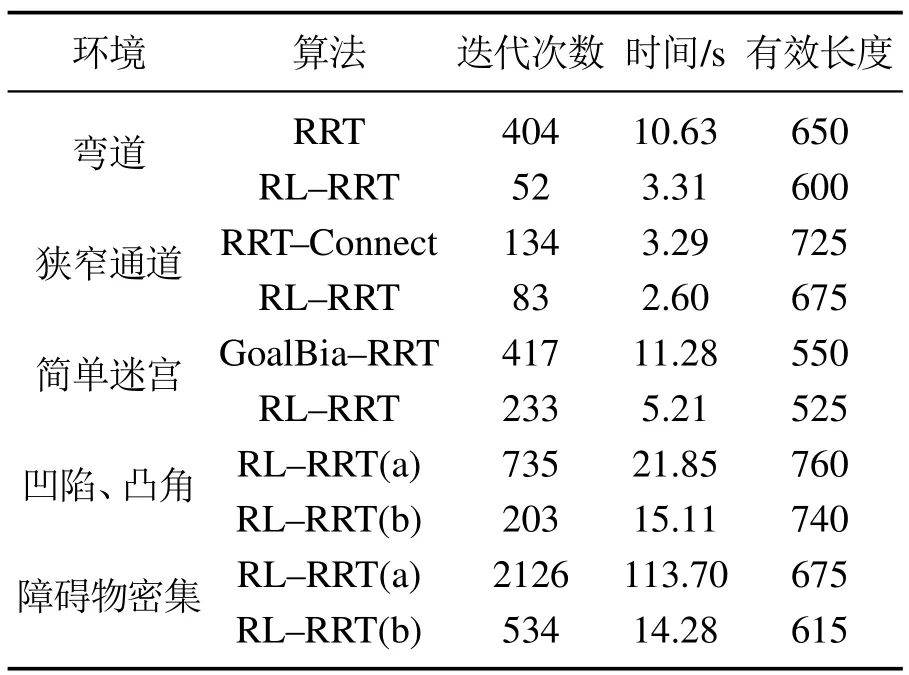
表2 RL-RRT和对比算法在不同环境性能比较Table 2 Comparison of different environmental performances of RL-RRT and comparison algorithms

如表1-2所示，表中列出的数据都是规划成功的数据统计结果.分析实验数据可以发现，弯道环境下，在有效节点树和节点总数比例上，RL-RRT算法比原始RRT算法高16%，如图12，RL-RRT算法有效节点的占比更高;在有效长度上，RL-RRT算法比RRT 算法少50步长;在时间效率上，RL-RRT算法比RRT算法快7 s.狭长狭窄通道环境下，RL-RRT算法有效节点的占比RRT-Connect算法高24%，如图12，RL-RRT算法有效节点的占比更高.简单迷宫环境下，RL-RRT算法在有效节点数和节点总数比例上比GoalBia-RRT算法高7%，如图12，RL-RRT算法有效节点的占比更高;在时间效率上，RL-RRT算法比GoalBia-RRT算法快6 s.总之，相同的环境，在时间效率上，RL-RRT算法比RRT，GoalBia-RRT和RRT-Connect算法花费的时间较少;在有效节点比例上，RL-RRT算法比RRT，GoalBia-RRT和RRT-Connect算法有效节点比例高，证明RL-RRT算法具有有效性和高效性.

本文不仅把RL-RRT算法与原始RRT，RRT-Connect和GoalBia-RRT算法进行对比，并且还与未考虑可行旋转角度约束或固定步长的RL-RRT算法对比，如图10-11所示.在凹陷、凸角通道环境下，由于有角度约束，RL-RRT规划的路径与未考虑角度约束的RL-RRT相比更平缓，如图10蓝色A区域所示，避免了直角等大角度的波动，RL-RRT算法的安全性和舒适性都有提升，这样平滑的路径更满足规划时所期望的;与不考虑旋转角度约束的RL-RRT算法相比，有效节点比例上高21%，在迭代次数上少532次，时间上少6 s，路径有效长度少20步长，如表1-2所示.在障碍物密集通道环境，RL-RRT 算法针对环境障碍物密集程度而设置相应的步长，快速通过密集环境，相反采用固定步长的RL-RRT算法会由于步长不合适，而无法迅速通过障碍物密集区域，如图11蓝色A和B区域所示，规划效率低;在有效节点数占节点总数比例上，基于障碍物密度的步长的RL-RRT算法比固定步长的RL-RRT算法高34%，迭代次数少1592次，路径有效长度少60步长，时间少99 s，如图12-13和表1-2所示.总之，在特殊环境下，RL-RRT算法有较强的适应性.

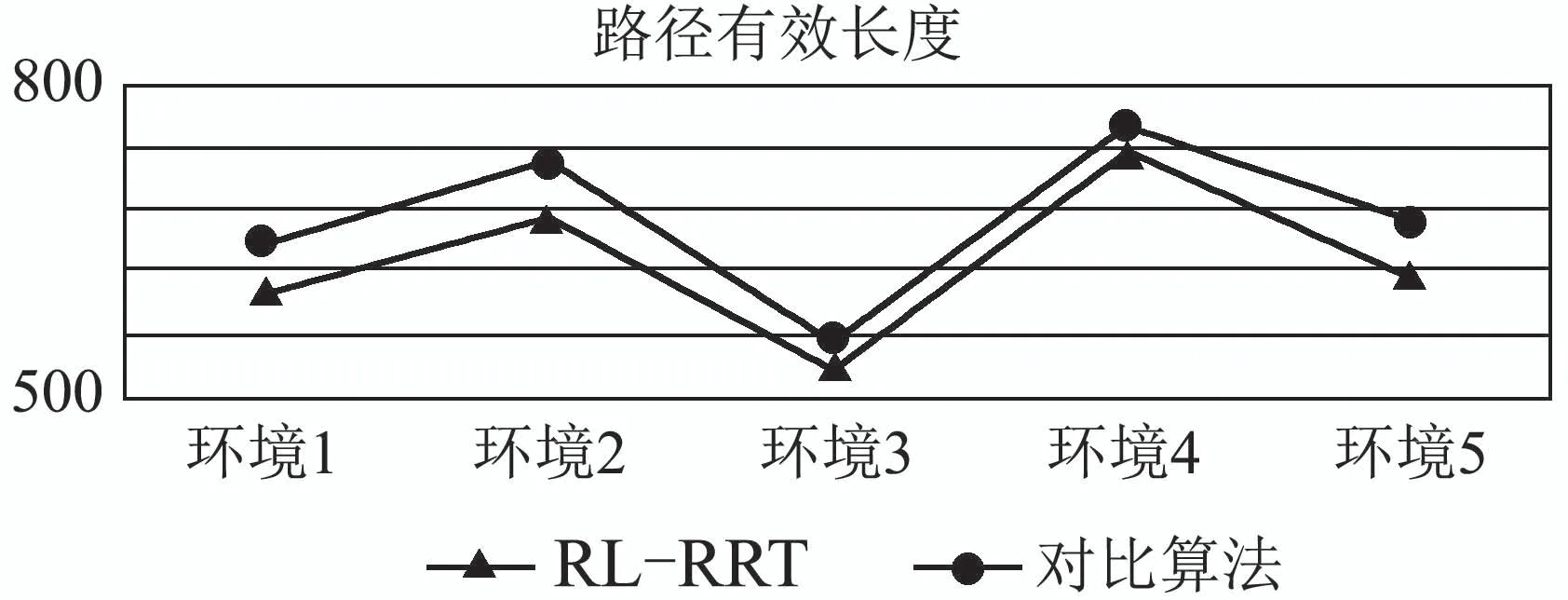
图13 比较RL-RRT和对比算法在5种环境路径有效长度Fig.13 Compare the effective length of RL-RRT and comparison algorithm in five environments

综上可以得出，RL-RRT算法具有3个方面的优点:首先，它具有类似RRT算法的探索能力，探索功能基于配置空间偏向Voronoi区域扩展，但RL-RRT避免了RRT和RRT-Connect算法的毫无目的的扩展问题，在躲避障碍物的基础上更有效地趋向目标点.其次，RL-RRT算法利用Sarsa(λ)方法，在节点扩展时选择高回报的节点，使得扩展树分支叶子节点数少、迭代次数少、规划路径短，在未知的配置空间中更高效寻找最优或近似最优解，实时性能较强.最后，RL-RRT算法在弯道、狭窄通道、简单迷宫、凹陷、凸角通道环境和障碍物密集的特殊环境下的有效性、高效性和适应性都比原始RRT，RRT-Connect和GoalBia-RRT算法高.

在同一环境下对比第1张图RRT算法和第2张图RL-RRT算法动作(即移动方向)的分布，如图14，会发现箭头方向是不同的，与RRT算法相比，RL-RRT算法箭头方向更有条理，说明节点随机性降低，并且指向目标区域的箭头的数量较多，能较快的收敛到目标点.这是由于RL-RRT产生的新节点总是处于靠近目标点，且性能评价好的位置，随机搜索树在每一次循环中作用发挥到最大，使得RL-RRT的收敛速度远快于原始RRT算法.

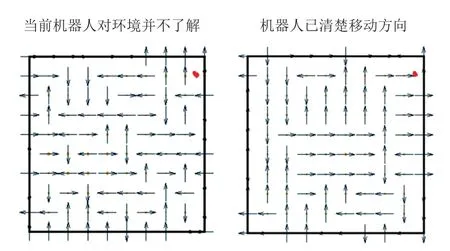
图14 收敛性分析Fig.14 Convergence analysis

4.1.2 不同k值对于RL-RRT的影响

在本文第3.3节随机节点的筛选中，设置优先选择躲避障碍物时k=0.7，而没有障碍物时k=0，现通过实验验证k权值改变后对算法性能的影响.相同环境下对比性能，无障碍物环境k权值设置为0，0.1，0.5和0.9;有障碍物环境k权值设置为0.1，0.5，0.7 和0.9.

表3-4为不同k值的实验结果.图15为无障碍物环境的实验对比.图16为有障碍物环境的实验对比.

表3 不同k值的实验结果Table 3 Experimental results with different k values

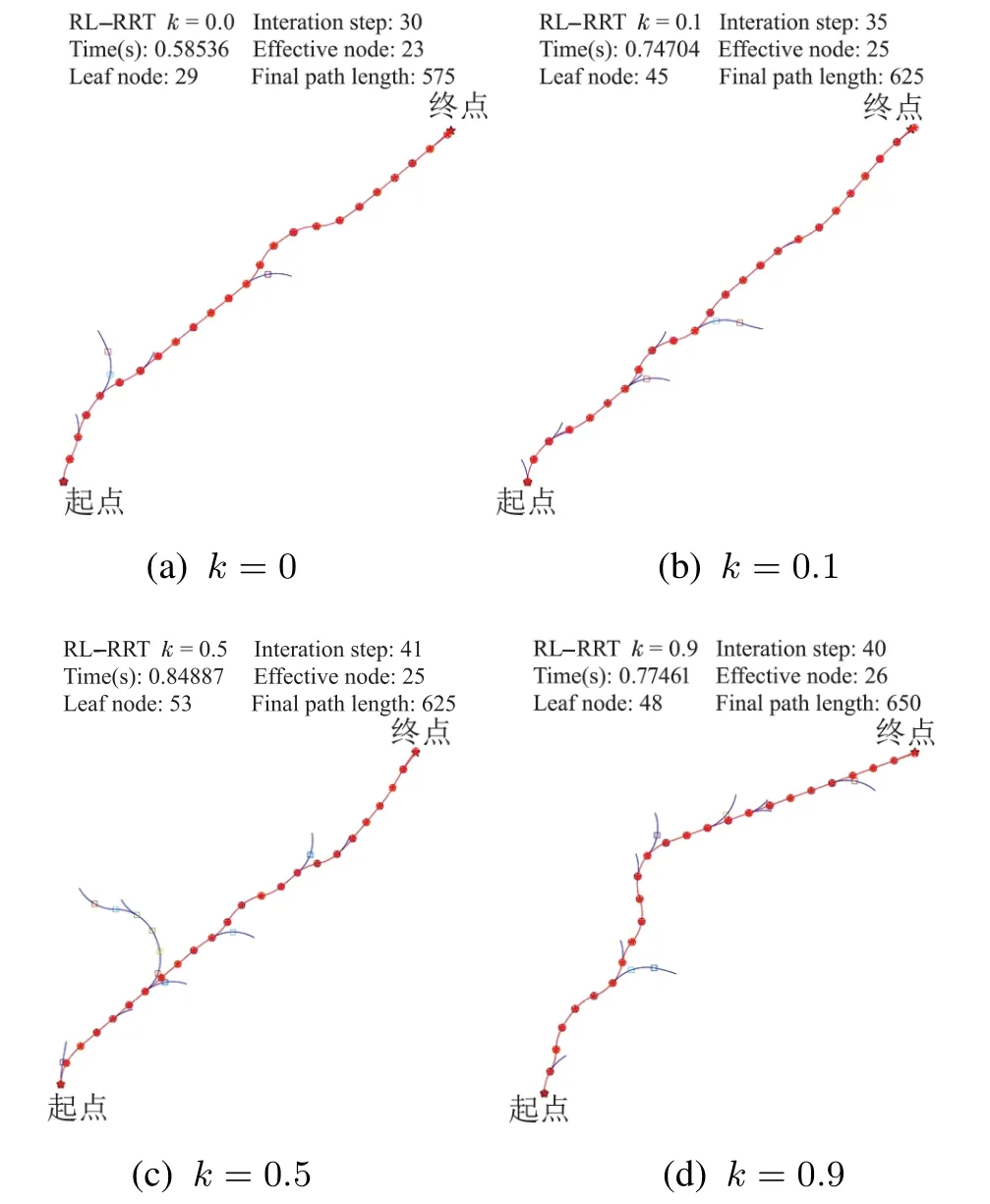
图15 不同k值的仿真图Fig.15 Simulation with different k

由图15和表3可知，无障碍物环境下，当k ＞0时，迭代次数上升，有效节点比例下降，避障时间增加，同时有效长度变长，总之性能下降.

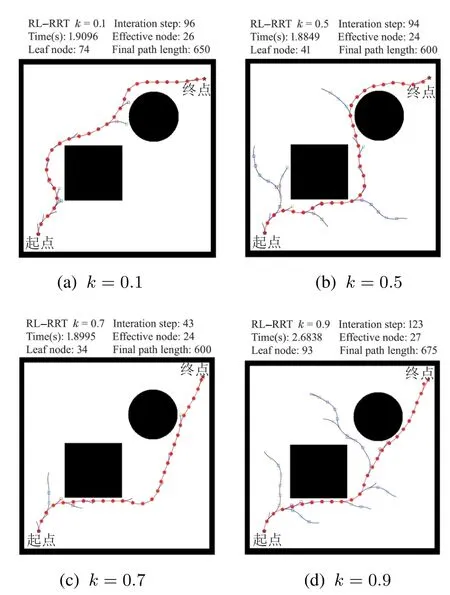
图16 不同k值的仿真图Fig.16 Simulation with different k

由图16和表4可知，有障碍物环境下，当k ＞0.7或k ＜0.7时，迭代次数上升，有效节点比例下降，避障时间增加，同时有效长度变长，总之性能下降.

表4 不同k值的实验结果Table 4 Experimental results with different k values

根据上述仿真实验，设置优先选择躲避障碍物k=0.7，而没有障碍物k=0时局部路径重规划效果最好.

4.2 ROS仿真实验

将ROS与Gazebo，Stage和Rviz相结合搭建仿真环境，进行3维仿真实验，模拟移动机器人TurtleBot2真实的实验场景.

4.2.1 移动机器人运动学模型

TurtleBot2是一款低成本、开放源代码的移动机器人.运动特性为两轮差速驱动，左右两轮为其提供动力，根据两轮的速度差实现移动机器人的转动运动.

为了可以准确的描述TurtleBot2的运动规律，需要两种参考坐标系来描述，分别为:TurtleBot2坐标系ORxRyR，世界坐标系OworldXworldYworld.在世界坐标系Xworld－Yworld下描述TurtleBot2的位姿信息用(xR，yR，θ)表示，其中θ为TurtleBot2移动方向的航向角，即TurtleBot2的朝向与横轴的夹角.TurtleBot2 机器人坐标系用xR－yR表示，速度用v表示，左轮和右轮的速度分别用vl和vr表示，旋转角速度用ω表示，左右两侧车轮的间距为L，右侧轮到圆心的距离为D，转弯半径为R.TurtleBot2在世界坐标系下的位置如图17所示.

图17 TurtleBot2在世界坐标系下的位置Fig.17 TurtleBot2's position in the world coordinate system

TurtleBot2移动机器人运动学模型可以描述为

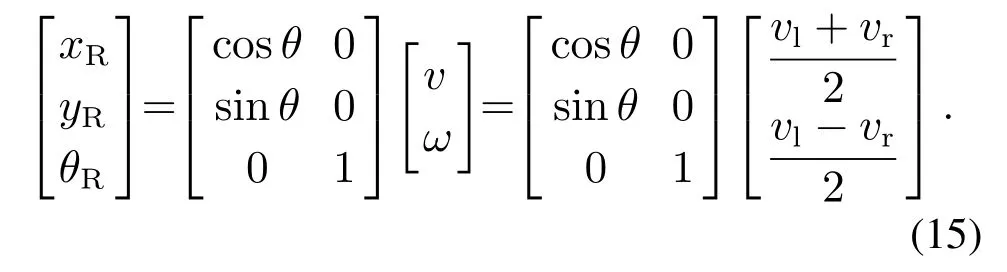
4.2.2 Gazebo仿真实验

Gazebo仿真环境为一个长度为13 m，宽度为12.5 m的三维仿真实验场景，墙壁的高度为2.5 m，厚度为0.15 m.障碍物区域长度为9.5 m，宽度为9 m，高度为0.4 m.如图18所示.移动机器人起点位置为(0，0，0)，目标点位置为(130，130，0)，环境四周为墙壁，移动机器人需要避开障碍物，穿过狭窄通道到达目标点.TurtleBot2机器人直径大小为351.55 mm，高度750 mm，最大速度设为0.65 m/s.TurtleBot2通过传感器来获取自身与障碍物的位置信息，同时用来确定机器人t时刻在环境中的状态.图19所示为移动机器人到达目标点的轨迹.

图18 实验场景Fig.18 Experimental scene

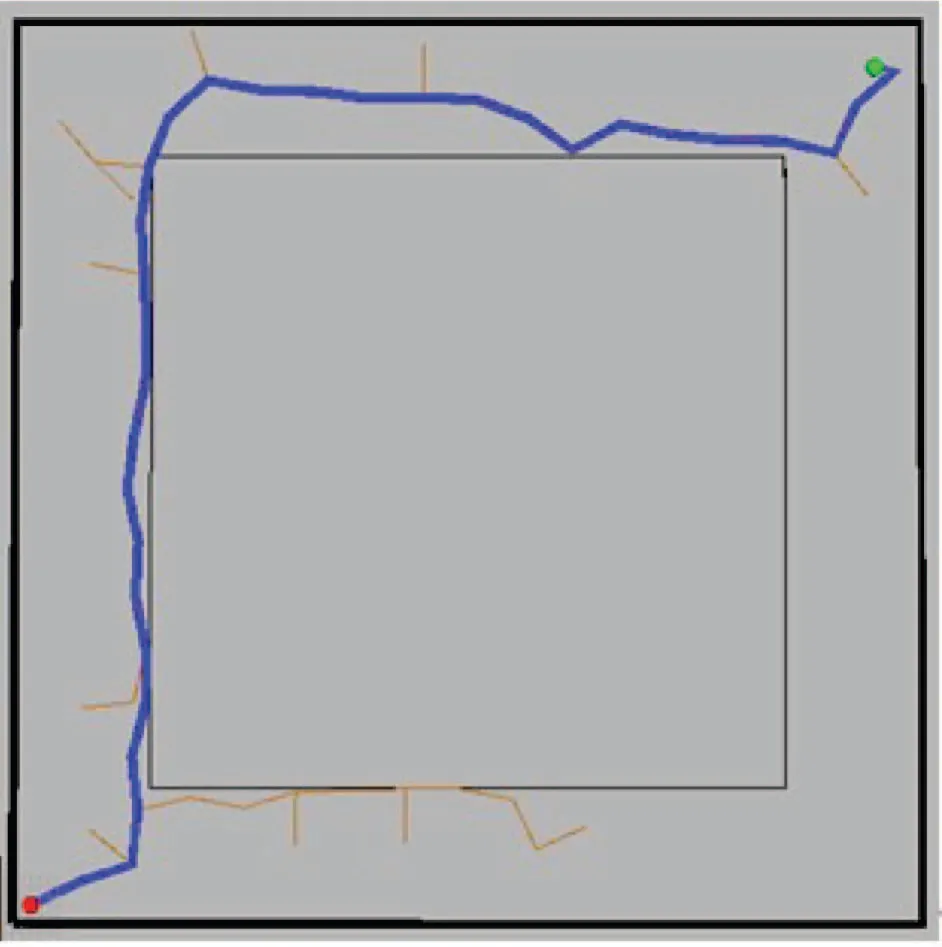
图19 RL-RRT的运动轨迹Fig.19 RL-RRT trajectory

4.2.3 Stage机器人仿真实验

通过给定移动机器人环境地图，一个起始位置，以及一个目标位置，启动Stage机器人仿真软件和一个Rviz实例，采用RL-RRT算法使Turtlebot2从某处自主移动到另外一处.Stage仿真环境表示一个长度为13 m，宽度为13 m 的三维仿真实验场景，墙壁的高度为2.5 m，厚度为0.15 m，如图20所示.移动机器人起点位置为(100，100，0)，目标点位置为(110，15，0)，环境四周为墙壁，移动机器人需要通过狭窄的通道到达目标点.Turtlebot2机器人直径大小为351.55 mm，高度750 mm，最大速度设为0.65 m/s.图21中灰色表示开放的区域，黑色表示障碍物，一系列绿色箭头表示位姿，绿色箭头即定位算法认为移动机器人可能所处的位置.

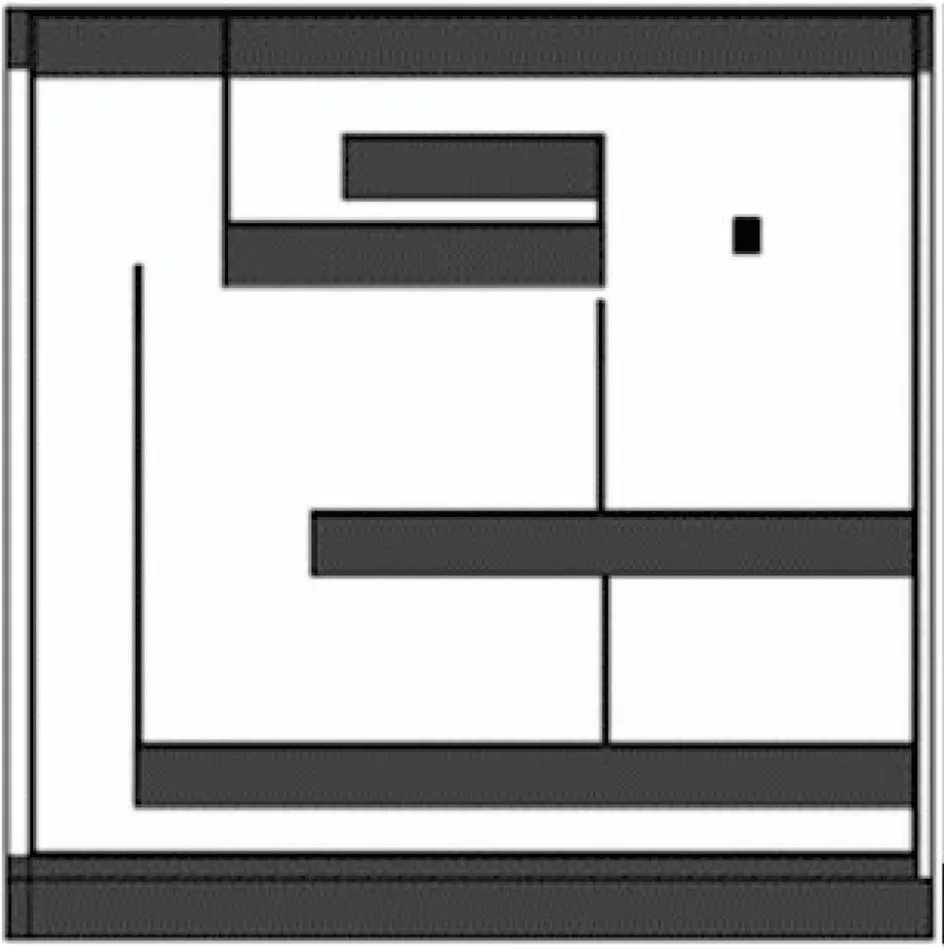
图20 三维仿真Fig.20 3D simulation

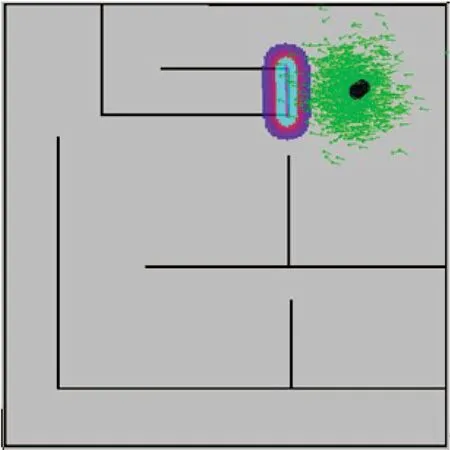
图21 初始位置Fig.21 The original location

全局规划使用路径规划算法和地图，规划一条从当前位置到目标位置的最短路径.然后这个最短路径被传入局部重规划中，局部重规划会试图驱动机器人沿着这个路径走.如果当机器人因为一些没有出现在地图中的障碍物而被挡住，局部重规划就会用传感器的信息绕开挡在机器人前面的障碍物，从错误中恢复过来.局部的评价地图和规划信息，如图22-23所示.其中紫红色表示好的、可以通过的位置，天蓝色表示不好的位置，如环境中的墙壁.

图22所示为移动机器人到达目标点的移动轨迹.当处在距离障碍物近的位置，根据扩展树各目标的权重，会先考虑安全，其次才是目标.在经过环境给予的奖励或惩罚的刺激后，会通过多步恰当的决策来达到一个目标，如节点处于障碍物环境，则产生负回报，则后继节点不再扩展;如果处于可行空间，则产生正向回报，逐步形成对刺激的预期，产生获得最大利益的习惯性行为.因此即使节点在靠近障碍物区域，由于到达目标后会得到高回报，在避障时同时会趋向目标移动，如图22所示.

与传统方法不同，基于强化学习Sarsa(λ)的RL-RRT算法解决局部路径重规划问题时并不需要建立环境模型，并且针对局部未知环境能为移动机器人利用经历的动作序列选择最优动作.因此当移动机器人的初始位置发生变化，而目标位置不改变时，并不需要重新规划，因为RL-RRT算法可以采用图22的Q值从新初始位置规划到目标点，如图23所示.

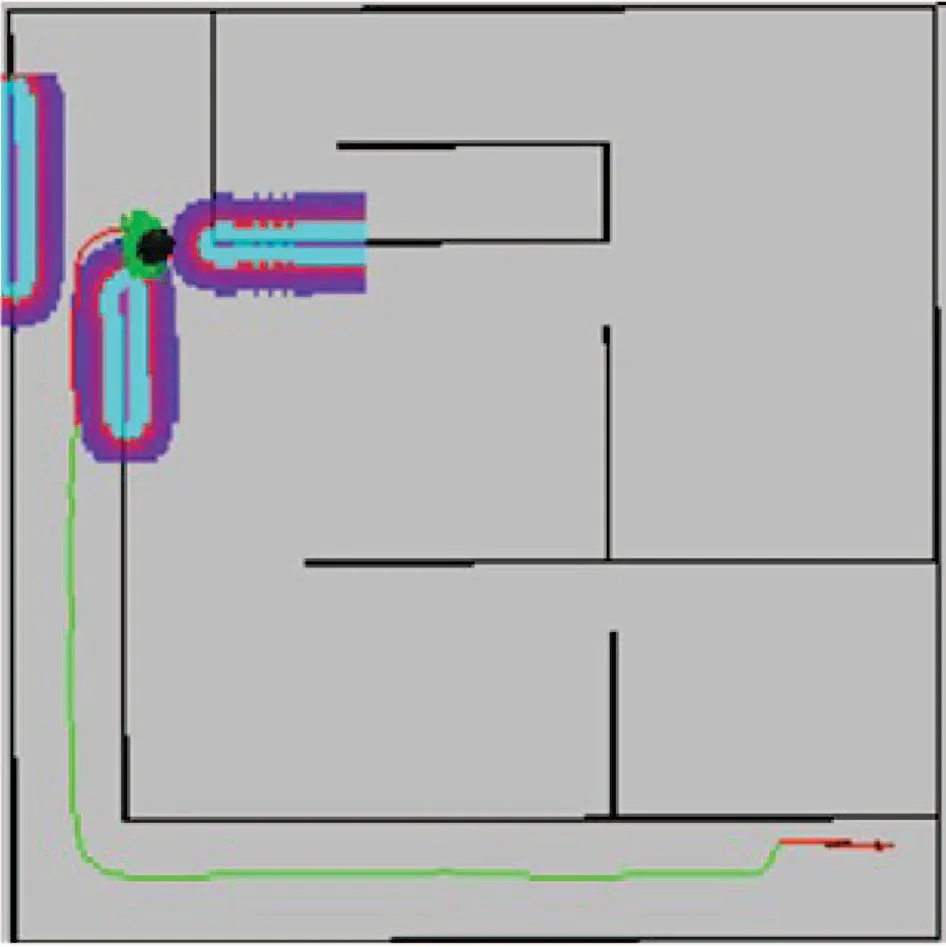
图22 目标位置Fig.22 The target location

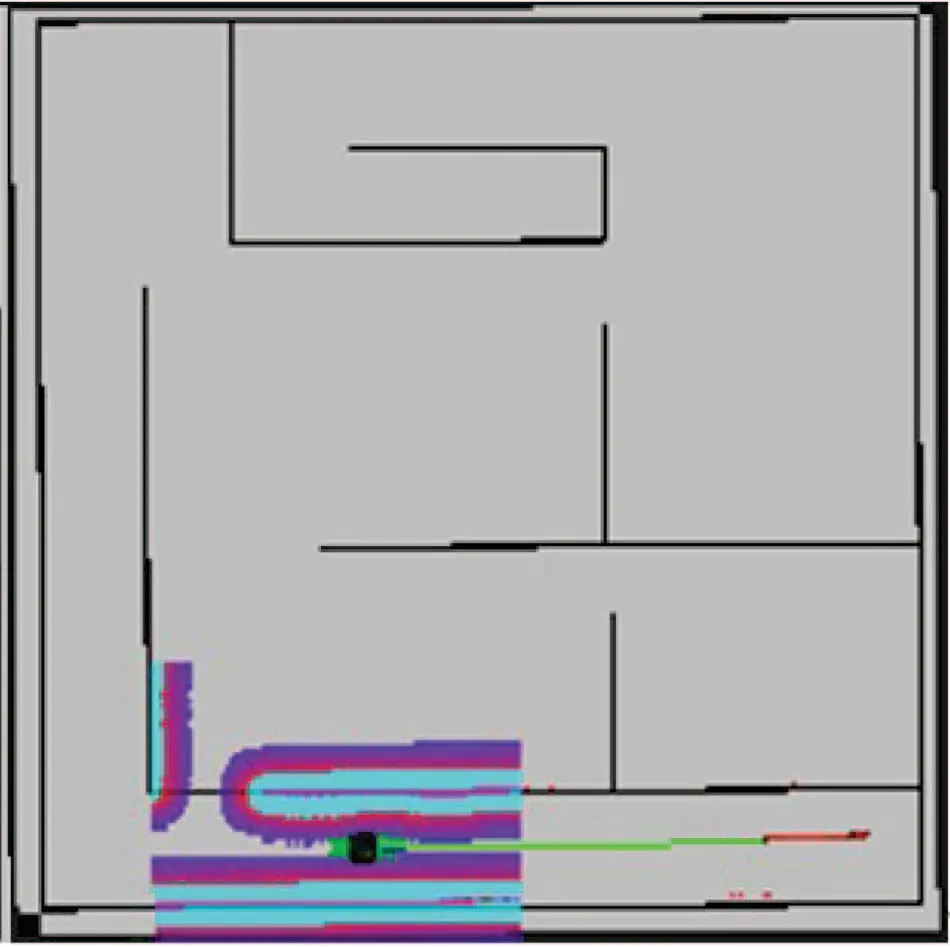
图23 新初始位置Fig.23 The new original location

5 结论

本文在路径规划算法方面，系统的论述了采用RL-RRT算法解决特殊环境下的机器人局部路径重规划问题，利用强化学习驱动的规划思想，学习避障策略，将预测控制与反馈机制有效结合起来，优化随机选点策略，降低RRT采样随机性;引入偏向目标思想，提升运动规划计算效率，使移动机器人在遇到障碍物时有较强的风险规避能力，以及目标趋向能力;同时融合两轮驱动移动机器人运动学约束条件，生成可执行曲线;最后将本文提出算法和原始RRT算法以及其变形算法进行仿真对比，并与未考虑可行旋转角度约束或固定步长的RL-RRT算法对比，验证了其在特殊环境下路径重规划应用中的高效性、有效性和适应性.

本文从提高路径规划效率出发，从一定程度上降低RRT算法采样的盲目性，提高避障效率，寻求一种能解决局部路径重规划方法.然而，好的算法只有通过现实环境才能证明其实用价值，后续的工作将围绕真实移动机器人来开展.此外，还可以进一步提升泛化能力，考虑更复杂的四轮驱动运动模型和更复杂的环境，以使得机器人能够更加适应动态、非结构化环境.