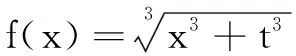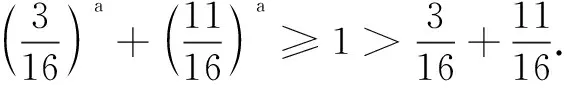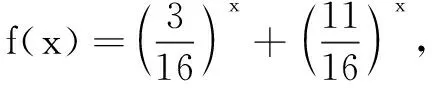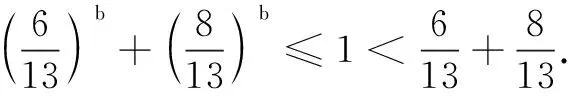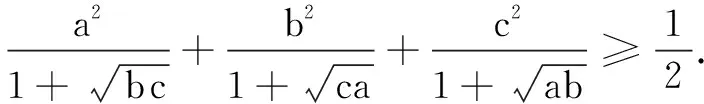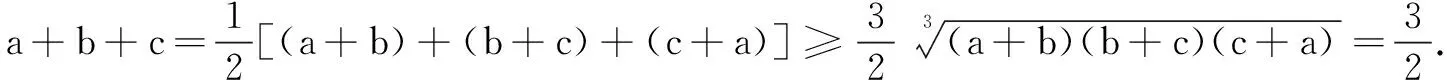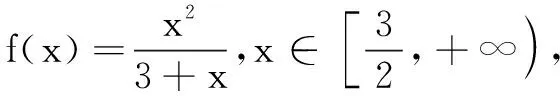构造函数 自然解题

张国治

(新疆生产建设兵团第二中学，830002)

构造法能为待解决的问题设计一个合理的框架,从而使问题转化并得到解决的方法[1].北京大学张筑生教授指出:有许许多多困难而有趣的数学竞赛题,虽有各种各样不同风格的解答,但读了这样的解答,在慨叹其无懈可击之余,也有几分遗憾.因为这种天衣无缝式的解答,往往没有提供线索说明解题的思路,不能回答读者必然要产生的疑问:“解题的方法是怎样想出来的?”为此,他呼吁“让解题的思路来得自然”[2]. 笔者发现：洞悉题设结构，巧妙构造函数,可自然地解答近年来部分高中数学联赛试题.兹分类例说如下，供读者参考.

一、求值

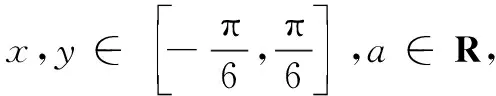
则cos(x+3y)=______.

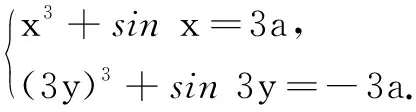
评注通过题设消除结构差异达到同构式,由此构造函数并利用其单调性解题,是解决此类问题的通法.

变式1(2016年山东省预赛题)设α,β分别满足方程α3-3α2+5α-4=0,β3-3β2+5β-2=0,则α+β=______.

解依题意,(α-1)3+2(α-1)2-1=0,(1-β)3+2(1-β)2-1=0.设f(x)=x3+2x-1,则有f(α-1)=f(1-β)=0.而f′(x)=3x2+2>0,f(x)在R上单调增,故α-1=1-β,即α+β=2.

变式2(2015年河南省预赛题)已知实数x,y满足2x=ln(x+y-1)+ln(x-y-1)+4,则2 015x2+2 016y3=______.

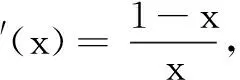
评注通过换元使此题解决更加简洁明了,而巧妙利用取等条件使问题完美解决.

二、求最值或参数取值范围

例2(2018年辽宁省预赛题)若正实数x,y满足x3+y3=(4x-5y)y,则y的最大值为______.

分析此题直接求解难度较大,解出y也会陷入误区.但利用“倍值换元”构造函数,便有如下自然的解法.

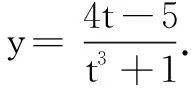
变式(2017年湖北省预赛题)已知正实数a,b满足ab(a+b)=4,则2a+b的最小值为______.

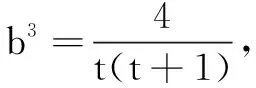
评注由例2及其变式不难发现,利用“倍值换元”,能使不易分离的双变量问题简单化,这是此类问题的求解通法.

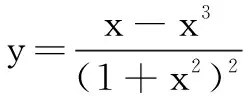
分析由函数表达式结构特征,联想到构造三角函数,可得简洁解法.

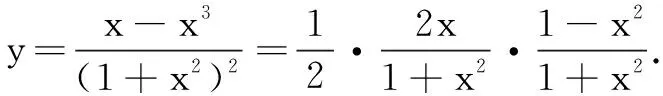
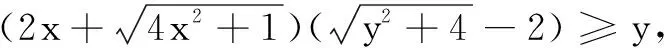
分析由题设条件式子中发现结构蕴含的共性,可利用同构化的意识整体把握构造函数求解.

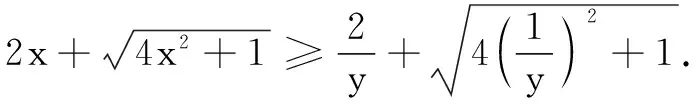
变式(2016年河南省预赛题)已知实数x,y满足2x+3y=4x+9y,试求U=8x+27y的取值范围.

解设a=2x,b=3y,则a,b>0,且a+b=a2+b2.

评注本题核心策略是从结构寻求差异,找到解题的突破口,其中整体换元思路显得尤为重要,而重要的代数变形使得构造函数自然生成.

三、解不等式

例5(2017年湖南省预赛题)设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f′(x),且有2f(x)+f′(x)>x2,则不等式(x+2 017)2f(x+2 017)-f(-1)>0的解集为______.

分析由条件不等式左边结构联想积的求导公式,变形得2xf(x)+xf′(x)

解结论不等式可化为

(x+2 017)2f(x+2 017)

>(-1)2f(-1).

①

设g(x)=x2f(x)(x<0),则g′(x)=2xf(x)+xf′(x)g(-1),可得x+2 017<-1,即x<-2 018.

变式(2018年广西壮族自治区预赛题)若定义在R上的函数f(x)满足f′(x)-2f(x)-4>0,f(0)=-1,则不等式f(x)>e2x-2的解为______.

提示设g(x)=e-2x[f(x)+2],则g(0)=1,g′(x)=e-2x[f′(x)-2f(x)-4]>0,g(x)在(-∞,+∞)单调增.又由f(x)>e2x-2,得e-2x[f(x)+2]>1,即g(x)>1=g(0),故x∈(0,+∞).

四、证明不等式

证明由条件,可得sin3β=sin3α+t3,且sinβ=3tsin2α+(3t2+1)sinα+t,两式相加,得

sin3β+sinβ=(sinα+t)3+sinα+t.

设f(x)=x3+x,则f(sinβ)=f(sinα+t),且f(x)在R上单调增,所以sinβ=sinα+t.代入sinβ=3tsin2α+(3t2+1)sinα+t,化简可得3tsin2α+3t2sinα=0,所以t=0或t=-sinα或sinα=0,即t=0或t=-sinα或t=sinβ.因此|t|≤1.

评注利用函数证明不等式常见思路是差值构造.

例7(2018年内蒙古自治区预赛题)设a,b∈R,且3a+11b=16a,6a+8b=13b,求证:a

所以假设不成立,从而原命题成立.

分析标准解答是用赫尔德不等式获证,略显繁琐.洞悉题设结构,巧妙构造函数,可使问题自然获解.

证明由柯西不等式,得