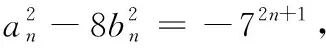高三数学综合测试
2020-09-04
一、填空题(本大题共14小题,每小题5分,计70分)
1.已知集合A={-1,1,2,3},B={x|x∈R,x2<3}, 则A∩B=______.
2.复数(a+i)(1+2i)是纯虚数(i是虚数单位),则实数a=______.
3.某算法的伪代码如图所示,如果输入的x值为32,则输出的y值为______.
Readx
Ifx≤5 Then
y←x2
Else
y←log2x
End If
Printy
4.现有三张识字卡片,分别写有“抗”、“疫”、“情”这三个字.将这三张卡片随机排序,则能组成“抗役情”的概率是______.
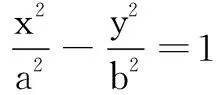
6.已知一组数据3,6,9,8,4,则该组数据的方差是______.

8.将1个半径为1的小铁球与1个底面周长为2π,高为4的铁制圆柱重新锻造成一个大铁球,则该大铁球的表面积为______.
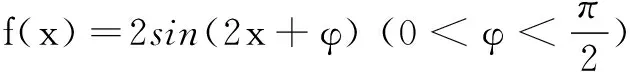
10.若正实数x,y满足x2+2xy-1=0,则2x+y的最小值为______.

12.已知对任意x∈(-∞,1)∪(5,+∞),都有x2-2(a-2)x+a>0,则实数a的取值范围是______.
13.在平面直角坐标系xOy中,圆C: (x+2)2+(y-m)2=3.若圆C存在以G为中点的弦AB,且AB=2GO, 则实数m的取值范围是______.
14.在∆ABC中,已知∠C=120°,tanA=3tanB, sinA=λsinB, 则实数λ=______.
二、解答题(本大题共6小题,共计90分.解答应写出必要的文字说明、证明过程或演算步骤)


(1)求cosB的值;
(2)求CD的长.
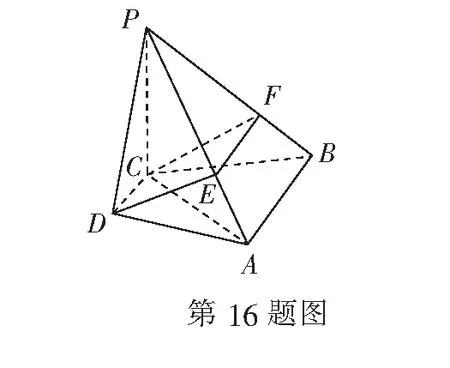
16.(本小题满分14分)如图,在四棱锥P-ABCD中,PC⊥平面ABCD,AB∥CD,CD⊥AC,过CD的平面分别与PA,PB交于点E,F.
(1)求证:CD⊥平面PAC;
(2)求证:AB∥EF.

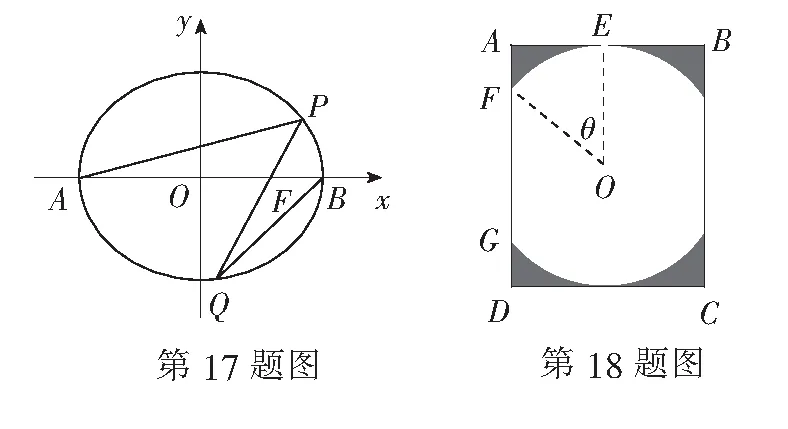
(1)若QF=2FP,求直线l的方程;
(2)设直线AP,BQ的斜率分别为k1,k2,是否存在常数λ,使得k1=λk2?若存在,求出λ的值;若不存在,请说明理由.

(1)求S关于θ的函数关系式,并求定义域;
(2)根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时,求边AB的长度.
19.(本小题满分16分)已知函数
f(x)=2 lnx-x2+ax(a∈R).
(1) 当a=2时,求f(x)的图象在x=1处的切线方程;

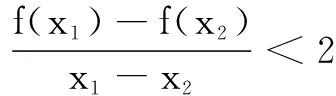

(1) 求{an},{bn}的通项公式:

附加题(本大题共4小题,每小题10分,计40分.解答应写出文字说明、证明过程或演算步骤)


22.(本小题满分10分)在平面直角坐标系xOy中,点F(1,0),直线x=-1与动直线y=n的交点为M,线段MF的中垂线与动直线y=n的交点为P.
(1) 求动点P的轨迹E的方程;
(2) 过动点M作曲线E的两条切线,切点分别为A,B,求证: ∠AMB的大小为定值.

(2) 求证:bn不能被5整除.
参考答案
一、填空题
二、解答题
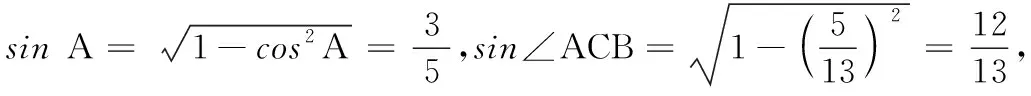
cosB=cos[π-(A+∠ACB)]
=-cos(A+∠ACB)
=sinAsin∠ACB-cosAcos∠ACB


16.(1)∵PC⊥平面ABCD,CD⊂平面ABCD,
∴CD⊥PC.
∵CD⊥AC,PC∩AC=C,∴CD⊥平面PAC.
(2)∵AB∥CD,∴CD∥平面PAB.
∵过CD的平面分别与PA,PB交于点E,F,
∴CD∥EF,从而AB∥EF.
17.(1)由a2=4,b2=3,得c=1.所以点F的坐标为(1,0).
设P(x1,y1),Q(x2,y2),直线l的方程为x=my+1,代入椭圆方程,得
(4+3m2)y2+6my-9=0,

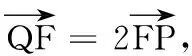
由A(-2,0),B(2,0),P(x1,y1),Q(x2,y2),x1=my1+1,x2=my2+1,可得

18.(1)过点O作OH⊥FG于点H,则易知∠OFH=∠EOF=θ,并且OH=OFsinθ=sinθ,FH=OFcosθ=cosθ.所以
S=4S∆OFH+4S扇形OEF
=sin 2θ+2θ.

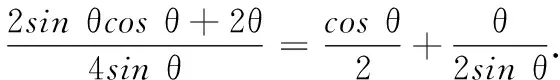
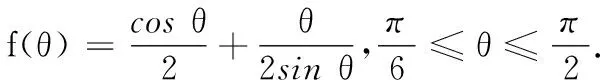


19.(1)y=2x-1. (过程略)
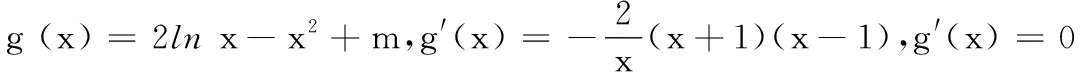



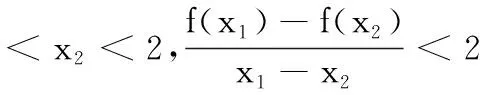

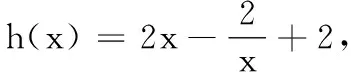
综上,实数a的取值范围是(-∞, 2].
20.(1)由Sn=2an-2,Sn-1=2an-1-2,两式相减,得an=2an-2an-1,则an=2an-1(n≥2).
由S1=2a1-2,得a1=2,故{an}是以2为首项,2为公比的等比数列,可得an=2n(n∈N*).
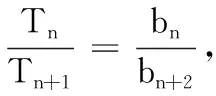
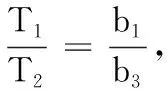
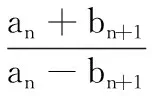

显然有2n+n+1>2n-(n+1),则c2=7>c3=3>c4>…>1,即存在n=2,3,使得b7=c2,b3=c3.

综上,满足要求的bn为b3,b7.
附加题

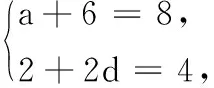
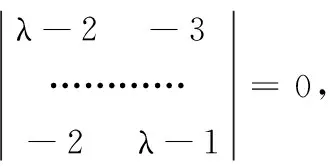
所以, 矩阵A的特征值λ=4或-1.
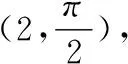

22.(1) 依题意,MP为点P到直线x=-1的距离,且MP=PF.所以点P的轨迹是抛物线,其焦点为F(1,0),准线为x=-1.所以,曲线E的方程为y2=4x.

ky2-4y+4k+4n=0.
令Δ1=16-4k(4k+4n)=0,得
k2+kn-1=0.
(*)
由Δ2=n2+4>0,知方程(*)有不相等实根k1,k2.由k1k2=-1,得∠AMB=90°.(定值)