面向工业电机考虑参数自调节的优化模型预测控制
2020-09-04颜晓花冯宝香
樊 星,颜晓花,冯宝香,李 力,李 昊
(1.国防科技工业技术开发中心, 西安 710061;2.华北科技学院安全工程学院,北京 065201)
近年来,资源紧缺以及环境问题逐渐影响到各个行业,国家对电动汽车的重视,因此电动汽车的研究占据了重要的一部分。由于异步电机结构简单、价格低廉等优点在工业领域应用较广。为了改善电机的运行效果,各种先进策略相继提出[1]。基于现代控制理论的先进控制策略对数学模型要求极高,对于电动机此类的高度非线性系统要得到精确数学模型相当困难。模型预测控制自20世纪70年代提出,至今在复杂工业上已经取得了巨大的发展。模型预测控制(MPC)成为了控制算法中一个有着较为丰富理论和实践内容的一个分支,有着巨大的发展潜力。
现如今,MPC因为其设计简单直观,动态响应快且能应对各种复杂、耦合、非线性多目标系统,建模简易无需精确模型等优点被人们逐渐重视。已经渐渐地应用于电力电子与电力传动领域并逐渐形成了有限集模型预测控制(FCS-MPC)分支[2]。该方法以电力电子变换器有限的控制状态为基础,依据被控对象的预测模型来预测未来系统状态的变化,在所有变化中选取对结果最有利,也就是最优控制量进行控制。该分支不仅有在变流器上的应用[3-5],对于高性能电机控制也开始应用,比如永磁同步电机的直接转矩控制或直接功率控制[6-7]。并针对FCS-MPC衍生了许多优化控制策略[8-10]。
该方法可以有效减少变流器开关次数,降低器件开关损耗,便于约束,动态性能好,但是其严重依赖所构建的预测模型。但传统MPC中,预测模型依旧有一部分参数未知,且由于大多预测模型采用的欧拉离散,然而采样以及计算的延时会导致预测模型失真。
文献[11]针对参数未知问题进行了研究,但且由于电机参数时变性强,使用场所不定,目前该方法只能暂时应用于有限的场所。文献[12]为了解决采样延时和计算延时,对模型进一步预测以补偿采样以及计算延时,但该方法没有从根本解决问题。且由于未来变量的不可测,预测步长越多精度越差,导致动态性能恶化。文献[13]虽然对预测模型进行了误差补偿,但是仍然无法较为精确地得到模型,在不同工况参数发生变化时控制效果将会大打折扣。
为解决该方法工况环境的敏感性、参数的鲁棒性等问题,并针对工业电机的实际情况,基于系统辨识提出一种无参数模型预测控制。该方法无需电机参数,使用静止坐标轴下的异步电机线性离散方程作为局部预测模型,使用最小二乘法对预测模型的系数在线估计更新。考虑到系统运气突变时可能造成系统参数突变问题,在弱磁运行区域针对优化。通过预测模型可以对未来的状态量和输出量进行预测。并针对电动车环境工况下,对弱磁控制时电动机的参数变化针对优化。仿真验证所提出策略在不同工况下的有效性。
1 数学模型及模型预测直接转矩控制
1.1 逆变器驱动异步电机数学模型
FCS-MPC以逆变器三桥臂的开关状态为控制量,输出一定的电压作用于异步电机的定子侧,以此驱动异步电机,如图1所示。

图1 电压型逆变器驱动异步电机模型Fig.1 Voltage-type inverter driven asynchronous motor model
由于在两相静止坐标系下可以降低异步电机数学模型维度,且其逆变器电压空间矢量表述也较为方便,因此使用异步电机在两相静止坐标系下的数学模型如下:[14]

(1)

(2)
式中:Rs、Rr分别为定子与转子电阻;Lr、Ls为定子转子电感;Lm为定转子互感;σ=1-Lm2/LrLs为电机漏磁系数;ψs、ψr分别为定子与转子磁链;np为电机极对数;Te为电机转矩;p为微分算子;ω为电机转子频率。逆变器数学模型如下:

(3)
定义开关函数:

(4)
容易得到异步电机磁链方程:

(5)
采用欧拉法可以得到离散化模型如下:


(6)
代入式(2)中可以得到转矩公式如下:

ψsα(k+1)ψrβ(k+1)]
(7)
由此可以根据逆变器桥臂开关状态得到对应的转矩以及磁链未来量。
1.2 模型预测直接功率控制
模型预测控制主要包括三个部分:预测模型,滚动优化、反馈校正。如图2所示。
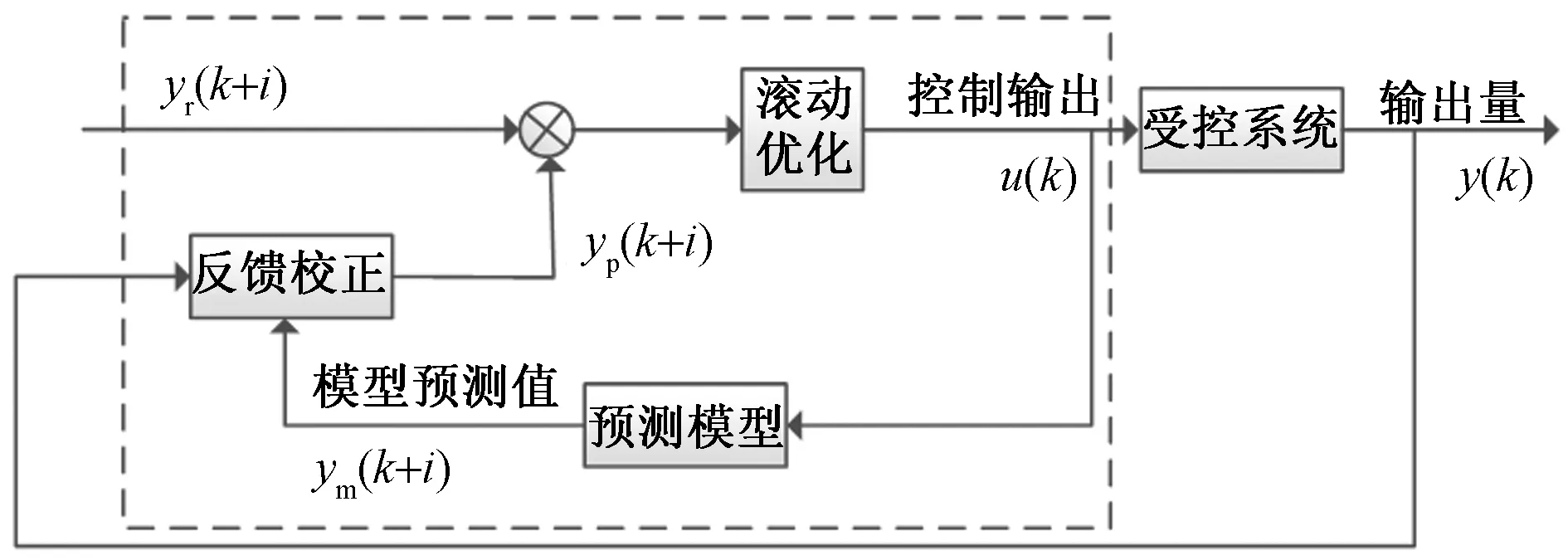
图2 模型预测控制原理图Fig.2 Schematic diagram of MPC
以式(6)和式(7)作为预测模型,通过对逆变器桥臂开关状态滚动计算选择与参考给定值最接近的开关状态也就是最优矢量。由于判断量有多个目标,为选择最优矢量,需要通过目标函数来对该矢量进行评估。通过引入目标函数来评估误差,误差越大则目标函数Gi越大,提出一种无须额外调试权重值的目标函数如式(8)所示:

(8)
通过平均分配其误差量,选择两个误差同时达到最小的一种电压矢量。通过该目标函数可以评估相应的开关矢量并选择最优开关状态输出给变流器桥臂从而对电机进行相应控制。
2 预测模型系数辨识
2.1 逆变器驱动异步电机数学模型
要得到一个较为精确的预测模型,往往使用系统辨识。传统的系统辨识往往假设系统为SISO动态系统,该辨识实际为一个黑箱辨识。当系统状态发生变化,辨识参数阶跃,导致系统动态性能恶化。并且神经网络以及群智能等算法的高纬度矩阵也并不适用于该系统的实时控制。
由于推导的离散系统方程为线性方程且参数较为稳定,可以在线更新局部线性模型集总参数去逼近电机的非线性系统。最小二乘法有着不需要高纬度矩阵且辨识过程简单的优点,因此选用最小二乘法作为模型参数的辨识方法。
将式(6)改写为

i=1,2,3,4
(9)
式(9)中:i代表方程的第i行,则每一行均可以写成最小二乘格式:
y(k)=φT(k)θ+e(k)
(10)
假设一共有N次观测,定义:
式(10)记为向量方程的形式:
YN=ΦNθ+eN
(11)
式(11)中,除待估计参数矩阵θ和误差值矩阵eN,所有量均可测。引入最小二乘准则:
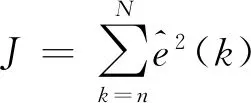
(12)

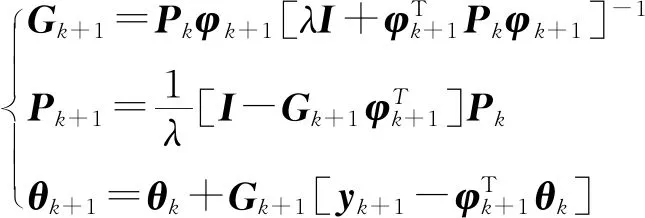
(13)
由式(13)可知,集总参数通常非常小。又因电机的高非线性,遗忘因子应取接近1的值以保证参数稳定性。初始状态矩阵θ0可以取一个适当值。
2.2 遗忘因子选取
当系统的状态改变时,希望它能更快地达到其准确值,则应适当减小权重。电动汽车环境下,弱磁运行时的系统状态改变较大,因此在工况变化时导致参数变化的情况需要考虑进遗忘因子的选取中。由定子磁链定向的d、q轴稳态电机公式如下:

(14)
电流电压约束条件:

(15)

a=0.999 9-0.000 9e-t
(16)
当达到条件重置时间变量t=0,从而达到减少遗忘因子随后恢复的目的。
2.3 基于系统辨识模型预测控制
模型预测控制相较于传统PI控制减少了PI个数,降低了工程中调参工作量。但是实际使用中仍然需要大量的参数辨识过程,且参数在运行过程中时变。为解决该问题,将系统辨识糅合进模型预测中,如图3所示。
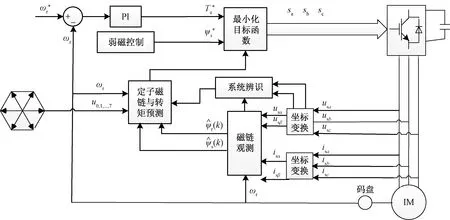
图3 基于系统辨识模型预测控制流程图Fig.3 Flow chart of SI-MPC
由图3可知,相较于传统定子磁链定向的4个PID,模型预测控制则只有1个,减少了前馈补偿以及工业调参,并由模型预测控制器直接给逆变器控制脉冲。将系统辨识过程添加进模型预测控制器中,无需再额外进行参数辨识。且系统辨识作为预测模型系数的给定模块,可以独立运行于模型预测模块之外,不会额外增加计算负担。
3 仿真验证
在MATLAB/Simulink中搭建仿真模型,电机额定功率为18.25 kW,额定电压220 V。对所提出的无参数模型预测控制策略算法的有效性进行验证,并针对转速阶跃、突加转矩工况与传统PID控制、传统模型预测直接转矩控制进行仿真对比。为保证统一性,所有策略均使用定子磁链定向控制,传统模型预测控制所使用参数为真实值的98%,逆变器设置采样周期Ts/5的采样以及计算延迟时间。首先进行对电机进行转速阶跃,得到结果如图4所示。

图4 转速阶跃Fig.4 Speed step
可以看到PID转速阶跃时电流平缓变化,几乎无冲击电流,但转矩有较大突变且转速变化较慢,无法达到快速跟随效果。模型预测控制,由于转速在3 s时刻突变,电流、转矩冲击都远远大于PID控制,且由于参数不准确等原因,转矩有一定脉动。所提出的无参数模型预测控制虽然在电流转矩冲击仍然较大,但相较于传统模型预测控制有所改善。且转速跟随快超调小。并测试突加转矩,如图5所示。
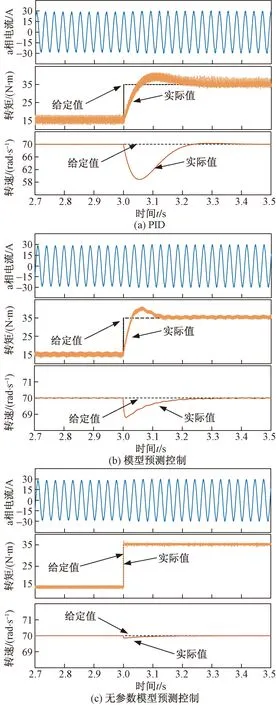
图5 转矩阶跃Fig.5 Torque step
由图5可知,突加转矩时刻,PID反应最慢,传统的MPC其次,且SI-MPC转速、电流无脉动,转矩波动小,体现了所提策略优秀的动态响应。为了验证该算法在复杂的工况下能够保持良好的动态响应,设置电动车运行,通过分析电动汽车在运行过程中存在的阻力形式(空气阻力、坡度阻力、加速阻力、滚动阻力),得出电动汽车行驶过程中的牵引力,将牵引力折算到电机轴,作为异步电机仿真时的负载,各阻力的数学公式如下:
Ft=Fw+Fr+Fn+Fm
(17)

(18)
式中:Ft为电动汽车的牵引力;Fw为空气阻力(无风时);Fr为滚动阻力;Fn为坡度阻力;Fm为加速阻力;ρ为空气阻尼系数;CD为空气密度;A为正面迎风的面积;α为坡度;fr摩擦系数。得到结果如图6(a)。
图6(a)为电动车加速运行,并在4 s时达到匀速状态。电动车力矩由电动车模型给出,加速状态下,由于有加速风阻等阻力相较于匀速状态受到的力矩较大。可以看到在转矩在4 s有较大的跌落,转速仍然仅有0.5 rad/s左右的冲击并快速回复给定值。在该情况下,所提出算法具有较好的动态响应。为了验证磁链变化较大的情况下,所提算法能否具有良好的鲁棒性。将其运行于工况2,如图6(b)所示。
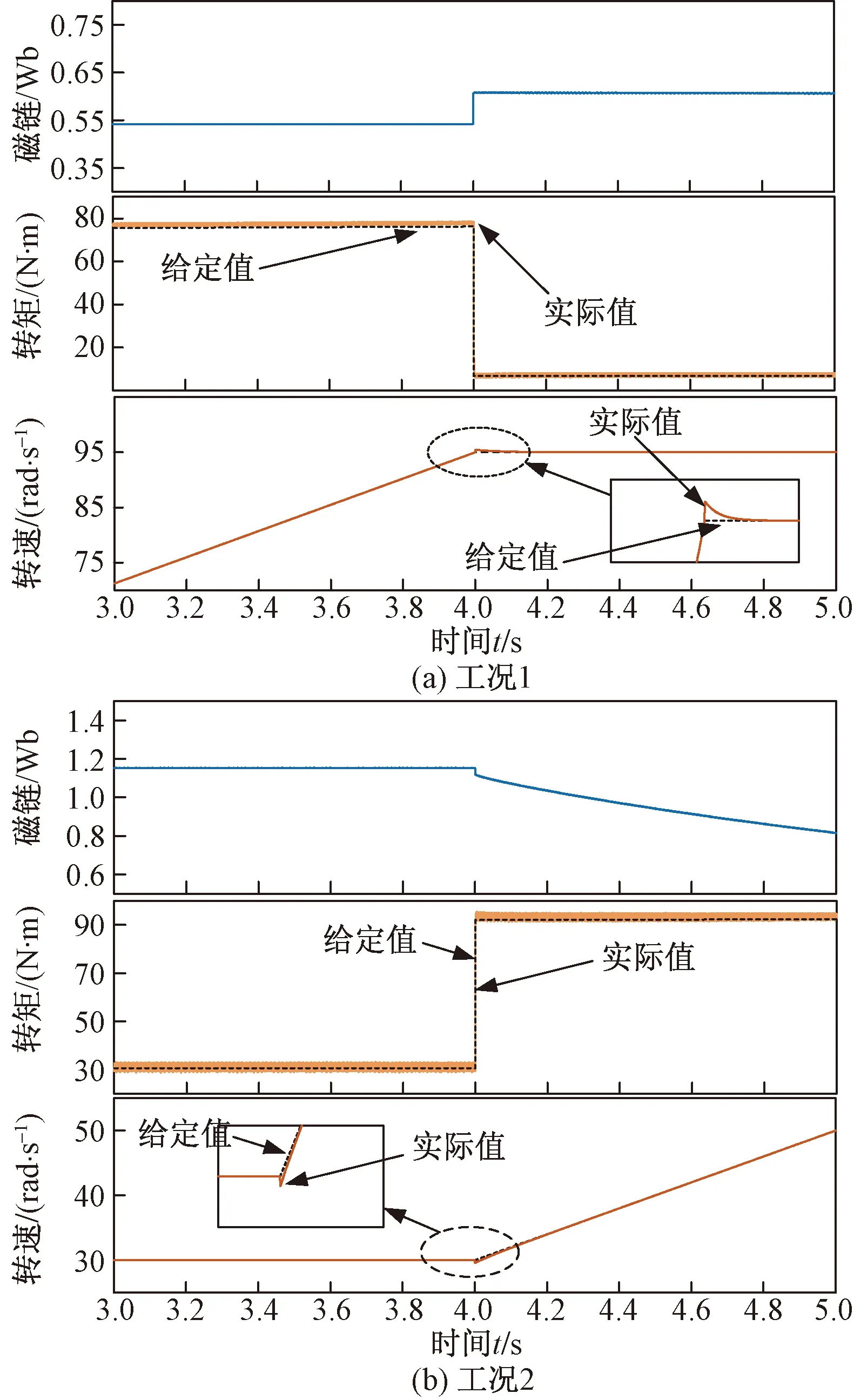
图6 无参数模型预测控制Fig.6 Control case
图6(b)为电动车匀速爬坡运行状态并在4 s后进入加速状态。可以看到4 s时刻突升转矩,并进入弱磁控制环节,在磁链变化较大的情况下,可以看到实际值跟随给定值效果良好。
4 结论
针对异步电机在工程应用中易出现的参数失配,采样及计算延时等问题,提出了一种无参数模型预测控制。可以得到以下结论。
(1)直接对离散模型的集总参数进行辨识,避免了多步长运行时导致的控制性能下降等问题。
(2)所提出控制由于是直接对未知参数进行辨识,减少了前期工作。
(3)在工况和参数未知的情况下,即便是复杂工况依旧能够达到良好的控制效果。
(4)验证了所提算法的预测模型能够精确预测,且控制器具有良好的鲁棒性以及动态性能。
