曲轴正反转向对齿轮噪声的影响

秦 剑

（江苏环球伟业服饰有限公司，江苏 徐州 221000）

一台单点机械压力机，在试车过程中出现齿轮噪声问题，依靠经验重磨齿轮后，未排除故障。后通过理论推导计算，找出校精度侧顶力是影响噪声的主要因素，采取减小校精度侧顶力的措施后，该问题顺利得到解决。

1 问题描述

一台300t单点冲床，传动系统如图1所示，滑块行程0.3m、冲次20spm，在试车过程中齿轮噪声问题突出，主要表现为滑块下行时噪声较大、滑块上行时噪声较小。将曲轴反转，即将驱动电机旋向接反、曲轴逆时针转向，滑块下行时噪声显著减小、上行时噪声也明显减小，检测曲轴反转比正转噪声小4～7dB。检查啮合的大齿轮和齿轮轴齿面，均为磨削成品。

2 原因分析

为便于分析，将上述齿轮噪声问题归为两种，一种是滑块一个行程内噪声的差异，即滑块下行噪声高于上行；另一种是曲轴正反转向导致的噪声差异，即顺时针转向（正转）高于曲轴逆时针转向（反转）。

2.1 齿轮噪声问题原因经验排查

对于上述噪声问题，首先根据经验法，采取与同类冲床噪声进行比较的方法进行判断。通过类比，滑块下行噪声比上行高1～2dB，是普遍现象；曲轴正转噪声比反转高1～3dB属正常范围。据此，制定解决方案如下。

2.1.1 滑块上行下行噪声差异

经检测，滑块下行噪声比上行高3dB，较合理区间值略高。滑块上下行噪声的差异，主要由工作机构间隙产生。

如图1所示，曲柄滑块机构共有三对摩擦副：曲轴轴颈与曲轴瓦、曲柄颈与连杆大头轴瓦、连杆小头（球头）与滑块球座。这三对摩擦副，设计总间隙约为0.7～0.8mm。平衡缸拉力在平衡掉滑块重量的同时，虽然消除部分总间隙，但至少要保留0.3mm以上的间隙，以保证正常润滑，避免摩擦副发热问题。滑块下行时，由于平衡缸拉力不断增大（容积减小、气压增大），各摩擦副由自由移动过渡到接触移动，产生冲击噪声；当滑块上行时，平衡缸拉力不断减小（容积增大、气压减小），各摩擦副由接触移动过渡到自由移动，冲击噪声显著减小。

调整平衡缸拉力，即调整平衡缸初始气压值，可抑制部分冲击噪声。因滑块上下行噪声差异不是主要矛盾，本例没有采取减小工作机构间隙的措施。

2.1.2 曲轴正反转噪声差异

依据检测结果，曲轴正转噪声比反转高4～7dB，超出合理区间值。产生异常噪声的原因，按以往经验判断，是大齿轮或齿轮轴的齿面磨削质量问题引起。由于齿面磨削采用的仿形磨削工艺，即在磨齿机上，将用金刚刀修整过的齿形砂轮，磨出左右齿面，如图2所示。因此，推断砂轮的一个齿形渐开线修整时误差较大，导致齿面接触较差，产生噪声问题。为验证分析结论，在齿轮轴齿面上涂上红油，和大齿轮进行配研，结果显示：曲轴正转时，驱动滑块运行的齿轮一侧齿面接触斑点，明显少于曲轴反转时另一侧齿面的接触斑点，说明反转齿面接触情况优于正转，证明分析结论成立。

为此，在磨齿机上重新修整砂轮，对修整过的砂轮进行检测，符合5级齿轮精度要求后，重磨齿轮轴和大齿轮。但是，修磨后的齿轮副重新装配试车后，噪声问题却依旧。

对此，决定从理论上分析，查找问题的根源。

2.2 曲轴正反转噪声差异溯源思路

依据齿轮噪声理论，除了齿轮材质自身因素外，噪声主要由力的方向和大小变化引起。在已排除齿轮加工、齿形渐开线的因素，即力的方向变化产生噪声的可能性后，接下来，对力的大小变化引起噪声的可能性，进行分析验证。

齿轮传递扭矩，主要依靠齿面法向力，齿轮轴传给大齿轮的齿面法向力（合力）分解情况，如图3所示，可知

从齿轮法向力分解情况可知，曲轴正反转向的差异，对径向分力Fjr的大小和方向都没有影响，因此可得出结论，圆周力Fjt是影响齿轮噪声的决定性因素。如求出曲轴正反转向时圆周力Fjt的不同，即可通过圆周力Fjt的计算公式，找出影响齿轮噪声的主要因素。

2.3 大齿轮圆周力计算

大齿轮，为曲柄滑块机构的运动转换输入端；滑块，为旋转运动转换成往复直线运动的输出终端。按照力的传导原理，可从运动终端的输出力，推导出曲轴（大齿轮）的输入扭矩力。按此思路，曲轴和滑块的中间连接为连杆，做出连杆的推力分解图，如图4所示，即可清晰反映出输入力和输出力两者之间的关系。

在空载和一定冲次条件下，从大齿轮输入力计算，忽略曲轴和连杆的惯性力、运动副的摩擦力，连杆推力在曲轴的切向分力Ft乘以曲轴偏心距R，为曲轴的转矩；而曲轴的转矩又等于大齿轮的输入扭矩，大齿轮的输入扭矩为分度圆半径Rj和圆周力Fjt的乘积，即

而 Ft＝F×cosγ，

2.3.1 连杆推力分解计算

从输出滑块力计算，连杆推力在滑块上的作用力，可分解为水平方向的分力F1、竖直方向的分力F2，即

同理，曲轴反转时

2.3.2 滑块受力分析计算

为求出连杆推力，做出滑块受力分析图进行求解，如图5所示。

图5中，滑块在水平方向受到的力，为平衡力；滑块在竖直方向受到的力，为非平衡力。当曲轴正转和反转时，滑块的受力状态发生变化，图5所示为滑块下行受力图（0°≤行程角 θ＜180°），图 6 所示为滑块上行受力图（180°≤行程角 θ＜360°），具体计算结果如下。

其中，m为滑块质量，a为滑块竖直方向加速度

由滑块受力情况可知，因滑块右侧导轨多了机床精度间隙调整机构，即顶丝装置。正常状态下，滑块重心和几何中心很难重叠，加之连杆斜向推力和平衡缸拉力的存在，实际上滑块在机身导轨内多是倾斜的，如图7所示，滑块受到的校精度侧向顶力，一般都大于零。

2.3.3 曲柄滑块机构运动计算

为求出滑块竖直方向的运动加速度，依据《机械设计手册》对心曲柄滑块机构近似式，参见图1和图4，可知

2.3.4 平衡缸拉力和导轨摩擦力计算；

要求出大齿轮的圆周力 Fjt，需先根据式（7）、（9）求出 F2，然后根据式（4）、（5）求出 F，最后由式（2）解出Fjt。

以曲轴正转为例，对式（7）进行求解

式中，平衡缸拉力Fb和导轨摩擦力Ff大小，由以下方法给出。

（1）平衡缸拉力Fb

图7中，两平衡缸大小相等，通过并联接头和冲床气包连通，气包容积约为两个平衡缸最大容积之和的7倍左右，故：

当H取最大值时Hm，即得单平衡缸最大容积Vbm

平衡缸气压Pb的求解说明：由于平衡缸活塞拉杆随滑块上下运动，活塞行程H等于滑块位移S。滑块上行时，气包将气体压进平衡缸；滑块下行时，平衡缸又将气体压进气包，因平衡缸的容积不断变化，平衡缸气压也在随之改变，但平衡缸气压和气包气压数值相等。由气体状态方程式可知，

其中，P为气体压强，V为气体体积，R为气体状态常数，T为气体温度。如将式（15）用于平衡缸气压的计算，将两个平衡缸气包容积和气包容积之和，当成一个气体体积，结合式（13）、（14）和式（15），则式（16）变形为

式（17）中，忽略气体温度T的变化，滑块处于行程内的的任意位置、即位移S（H）在（0，0.3）区间内取任意值时，RT数值不变，得

式（18）中，当滑块处于上死点位置、即位移S上=0.3m时，平衡缸拉力Fb可分解为两个分力，一个分力平衡掉滑块重量，另一个分力平衡掉模具上模重量。平衡掉滑块重量的分力等于滑块重量G，该分力的平衡缸气压设计值为0.3MPa，即活塞面积Ab与0.3MPa的乘积等于G；另一个平衡掉模具上模重量，该分力的平衡缸气压设定值区间为0～0.15MPa，即活塞面积Ab与设定值的乘积等于模具上模重量。空载试车时，虽然不带模具，但平衡缸初始气压值（滑块处于上死点）一般调整为0.33MPa左右，则式（18）变形为

将式（19）代入式（15）中，得

（2）导轨摩擦力Ff

由式（8）Ff=μ（F1+Fp）可知，要求出导轨摩擦力，需先求出校精度侧顶力Fp。

校精度侧顶力Fp，主要是由顶丝预紧力决定，见图7。实际上，在进行右导轨调整机构设计时，一个顶丝周围还至少设计两个拉丝，将右导轨拉向机身，以方便调整导轨位置，因此校精度侧顶力Fp不便用公式求出，只有依据经验值给定。导轨摩擦系数μ，一般取值 0.1，把式（3）代入式（8）

将式（21），代入式（7），得

曲轴反转时，逆向连杆推力Fa的竖向分力F2′的求解，由式（9）知

其中，平衡缸拉力Fb和曲轴正转时相同，Ff′可由（10）式 Ff′=μF1′进行计算，将式（6）代入式（10），得

将式（23），代入式（9），得

2.3.5 大齿轮圆周力计算

曲轴正转时，将式（4）代入式（2），得大齿轮圆周力Fjt为

曲轴反转时，将式（5）代入式（2），得大齿轮圆周力 Fjt′为

由三角形计算公式，结合图1和图4，得

为方便计算，联立式 （1）、（11）、（12）、（20）、（22）、（24）、（25）、（26）、（27），做成《大齿轮圆周力计算表》EXCEL表格，如表1所示。

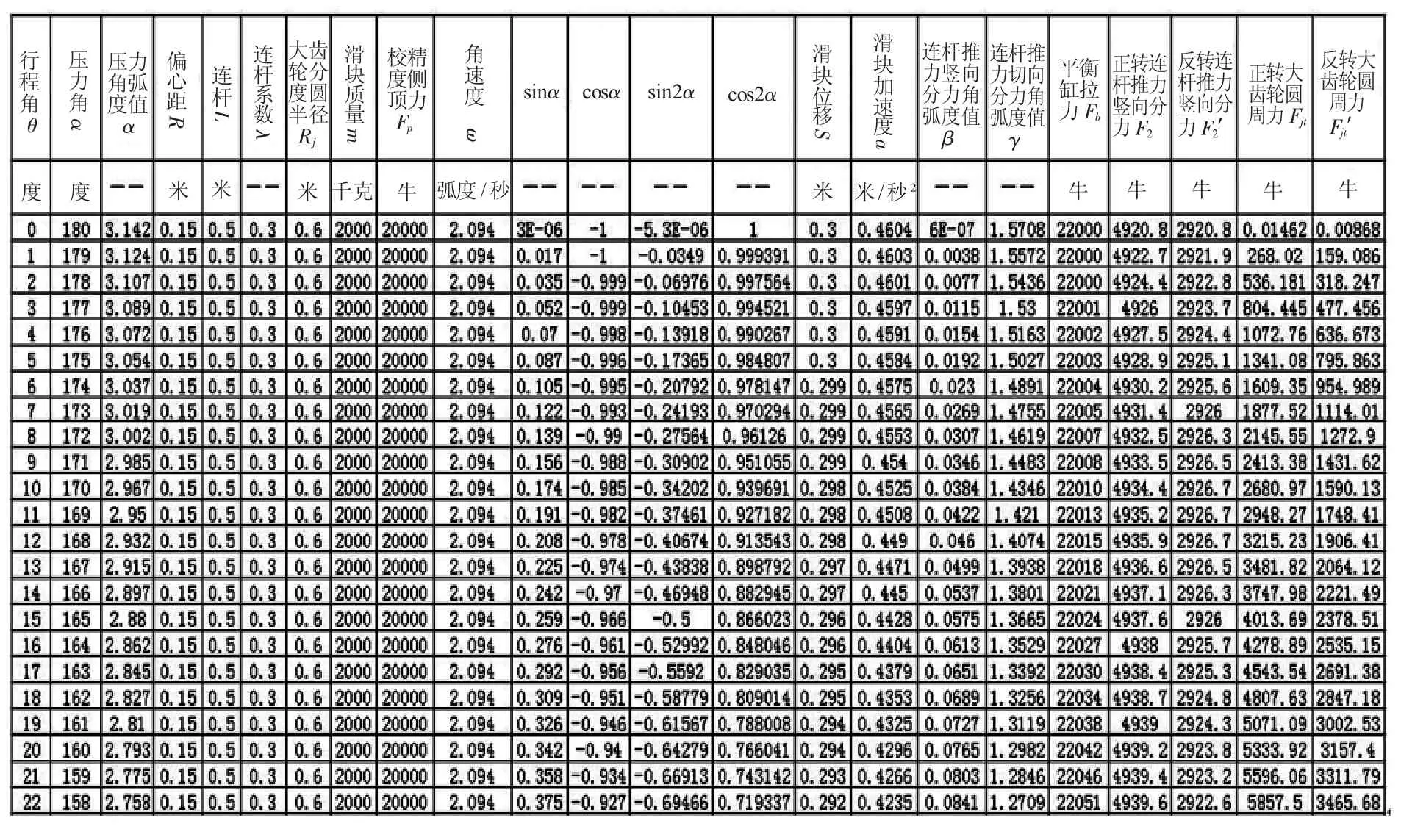
表1 大齿轮圆周力计算表

表格中，计算时压力角α取值在[-π，π]，故

另外，校精度侧顶力Fp暂估值为20000N。

2.3.6 大齿轮圆周力曲线图

为对比滑块一个行程内，曲轴正反转向时圆周力Fjt的不同，依据《大齿轮圆周力计算表》，作出大齿轮圆周力曲线图，如图8所示。

2.4 正反转齿轮噪声差异要因分析

曲轴正反转对比：由式（22）和（24）可知，反转时，滑块水平方向受力比曲轴正转少了一个校精度侧顶力Fp，竖直方向受力也少了一个Fp产生的摩擦力μFp。该摩擦力μFp对大齿轮圆周力的影响，见图9所示。当Fp为零时，正反转大齿轮圆周力相同；随着Fp值增大，Fjt和Fjt′的曲线差异越来越大。

因此，校精度侧顶力Fp的大小，是影响曲轴正反转齿轮噪声差异的主要因素。

3 解决方案和实施效果

由于校精度侧顶力Fp的大小影响齿轮噪声，如果曲轴反转时噪声低于标准要求4～6dB，则可通过减小Fp数值的措施，实现降噪的目标。本例中，采取重新修铣机身和滑块导轨、改进机床精度校正方法等，将曲轴正转时的齿轮噪声控制在了标准要求之内。

而另一台单点冲床齿轮噪声问题，因曲轴反转时噪声已接近标准要求的上限、正转时噪声远超标准，该例已不适用通过减小Fp数值的措施，实现降噪目标。依据齿轮噪声理论，该例在排除齿轮力的方向、大小因素后，剩下的因素只有齿轮的材质和硬度。查：大齿轮材料为ZG35SiMn，热处理正火硬度HB260；齿轮轴材料为 40Cr，热处理调质硬度HB220-250，齿面淬火硬度HRC38～42。大齿轮和齿轮轴材料已使用多年，材料因素可以排除。该例制定的解决对策为，降低齿轮轴齿面硬度，即取消淬火工序，将原来的热处理调质硬度由HB220-250改为HB260-280。该方案应用后，齿轮噪声降到标准分贝值以下。

另外，依据红油配研接触斑点得出错误结论的原因，通过查阅资料和进行试验显示，用红油配研检验齿面接触斑点时，有个弊端，当齿轮受力变化速率慢时，齿面接触斑点多；当齿轮受力突变、即变化速率快时，齿面接触斑点少，影响正确判断。

4 小结

“从实践到理论，从理论到实践”，在齿轮噪声原因查找的过程中得到了诠释。有些压力机故障问题，当凭经验不能排除时，不妨做个理论模型，进行公式推导，有时会起到事倍功半的效果。