基于结构自适应滤波方法的非线性系统辨识

冯子凯，陈立家，刘名果，袁蒙恩

（河南大学物理与电子学院，河南开封475000）

0 引言

系统辨识被广泛用于化学、机械、电气和土木工程等领域的系统控制和过程优化。一些系统的模型可以用线性参数形式表示，并且可以应用自适应控制来实现输出跟踪，对其未知的系统参数进行在线识别和估计［1-3］。例如，线性自适应滤波器被广泛用于系统建模［3］。尽管线性滤波器很流行，但在许多情况下仍然不适用，尤其是对于非线性系统的建模。

在实际工程中，大多数系统的模型不是线性的，并且在执行测量或设计和校准测量仪器时必须考虑其非线性特性。过去的几十年中，大量的研究集中于非线性系统的系统建模和识别［4］。

在对非线性系统建模和辨识时，面向块的模型被广泛应用，例如 Wiener［4-7］、Hammerstein［8］和 Wiener-Hammerstein［9-12］是很好的解决方案，可以基于简单的块构建模型，找到可以覆盖许多实际非线性系统的系统参数。例如，文献［4］中使用多项式非线性分数状态空间方程来描述非线性模型，扩展了输出误差方法（Levenberg Marquard 算法），以估计分数维纳系统；文献［8］中提出了一种可分离的非线性最小二乘算法来识别输出非线性块和Hammerstein子模型；文献［10］中提出了一个基于块的非线性分数模型，基于基准函数来识别Wiener-Hammerstein 模型。以上研究所用的模型有一个共同的特点是：它们的结构是固定的或者灵活性较低，而它们对系统的辨识是基于参数的辨识，因此具有一定的局限性。

相比之下，神经网络可被视为一类非线性的面向块的自适应滤波器。无论是横向滤波还是递归滤波，神经网络由于其良好的非线性逼近能力而受到了研究者的青睐［13-17］。然而，神经网络仍存在一些局限性。例如，它的自由参数总数（连接权重）通常超过1 000［17］，因此计算量较大，训练时间较长，且成本较高。

针对以上问题，本文提出了一种基于子系统的结构自适应滤波（Subsystem-based Structural Adaptive Filtering，SSAF）方法用于非线性系统的辨识。该方法由若干线性-非线性混合结构的子系统随机无反馈级联构成，并引入一种自适应多精英引导的复合差分进化（Adaptive Multiple-Elites-guided Composite Differential Evolution with a shift mechanism，AMECoDEs）算法［18］用于优化子系统的参数以及子系统之间的连接。本文最后验证了提出的方法可以很好地用于具有高度非线性的系统辨识。

1 自适应多精英引导的复合差分进化算法

AMECoDEs 算法引入了多重精英引导突变和转移机制来平衡收敛和多样性，与单纯的精英突变相比，在防止早期收敛和停滞方面更为有效。

AMECoDEs 算法与传统的差分进化（Differential Evolution，DE）算法相比有两个改进。第一个改进是多精英引导突变，使用精英（优秀的个体）信息的突变策略建议在探索与开发之间取得平衡。在传统的由精英指导的差分算法中，种群的个体通常只由一位精英指导，当选定的精英被定位在一个地区时，很容易将个体引向一个未知地区。在AMECoDEs 算法中，种群的每一个个体都受到两位精英的指导，这样可以减少被误解的可能性，并有效地使个体朝着更好的前景发展。每一位精英都是由一代向量生成策略创建的，并有不同的选择方法和参数，参数根据初步经验进行独立的自适应调整。第二个改进是引入了转移机制（Shift Mechanism，SM）。在SM中，如果种群不能收敛到一个小的区域，一些没有希望的个体将被转移到一个有希望的社区，以促进收敛；如果种群集中在一个很小的区域，一些没有希望的个体将无条件地转移到随机位置，以增强种群的多样性。AMECoDEs算法的步骤如下：

1）随机生成N 个命令序列。命令序列被视为目标向量，每个命令序列代表一个结构随机的非线性系统。产生初始种群P0。

2）计算目标向量的适应值，确定适应值是否满足全局最优条件。如果满足则输出最佳个体，结束计算；否则，执行3）。

6）算子M1 和M2 使用相同的库A，如果库A 的大小超过种群的大小PS，则会随机删除多余的个体。每一代结束时，启动转移机制。

7）返回2）进行比较。

AMECoDEs算法的伪代码如下：

2 结构自适应滤波模型

2.1 子系统

本文提出的自适应滤波模型由多个子系统组成，每个子系统为一个类型可选的一阶子系统或二阶子系统。一阶子系统由1 个延迟器、2 个乘法器、2 个加法器和1 个静态非线性函数组成；二阶子系统由2 个延迟器、4 个乘法器、3 个加法器和1个静态非线性函数组成。

一阶子系统如图1（a）所示，其中：A1和B1表示乘法器，z-1表示单位延迟，3 个黑点表示加法器，箭头表示信号流向；二阶子系统如图1（b）所示，其中：A1、A2、B1和B2表示乘法器，z-1表示单位延迟，3个黑点表示加法器，箭头表示信号流方向。

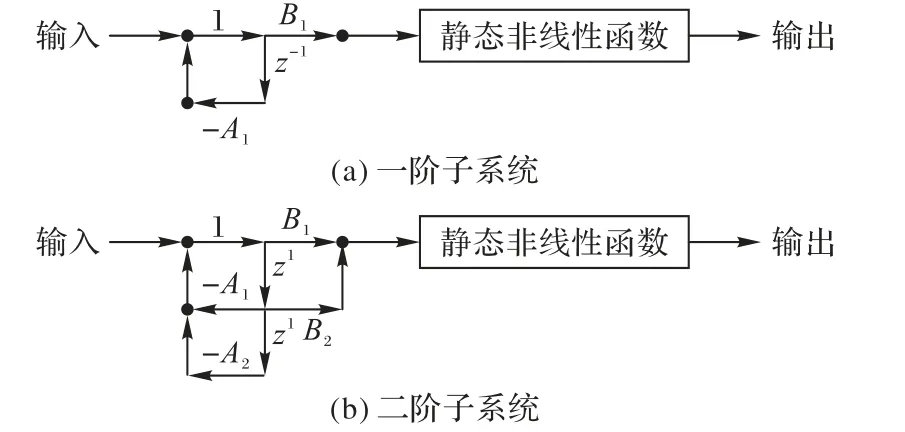
图1 子系统结构示意图Fig.1 Schematic diagram of subsystem structure

为了便于叙述，将一阶子系统和二阶子系统简称为子系统。式（1）表示一阶子系统线性部分的传递函数，其中R为实数域，A1的取值范围为(-1，1)，使传递函数的极点位于单位圆内，确保了一阶子系统线性部分的稳定性。

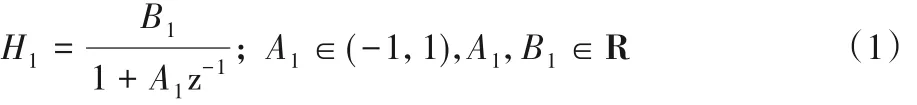
式（2）表示二阶子系统线性部分的传递函数，其中R为实数域，C 为复数域；a1和a2的取值范围使传递函数的极点限制在单位圆内，保证了二阶子系统线性部分的稳定性。

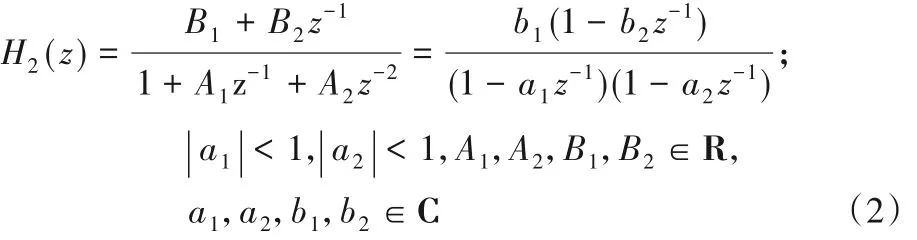
一阶子系统和二阶子系统的非线性部分有几种选择：

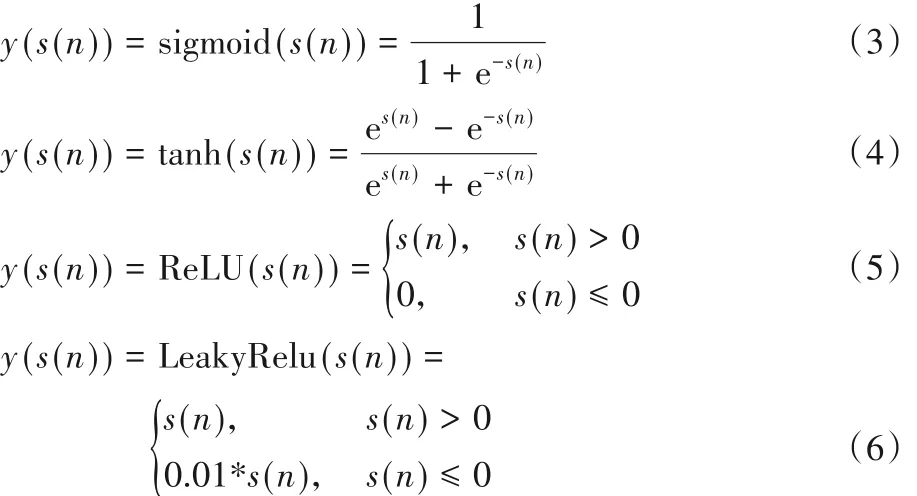
其中：s（n）为自变量，y（s（n））为系统输出；式（4）中，e 为自然常数。Sigmoid 函数是最常用的非线性函数之一，被广泛应用［19］，故本文子系统的静态非线性函数统一设置为Sigmoid函数。

2.2 优化问题描述

2.2.1 算法个体信息描述

在AMECoDEs 算法中，每个单独的个体（θ）称为一条指令。一个个体包含i个子系统，每个子系统所包含的信息有：输入端口号（I）；输出端口号（O）；子系统类型（T），即一阶子系统或二阶子系统；连接方式C，分C1、C2、C3三种；子系统线性部分的参数（P）。

AMECoDEs 算法中每个个体的结构如图2 所示。其中矩阵θ和矩阵的表达式如式（7）和式（8）所示。

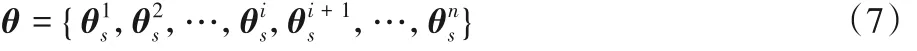
图2 单个个体的结构Fig. 2 Structure of each individual

2.2.2 子系统连接方式

子系统的连接方式有三种：连接新的活动端口（C1）、连接现有端口（C2）和连接系统的输入端口（C3）。C1是生成一个新的活动端口，即新添加的子系统的输入端口连接到当前的活动端口，其输出端口连接到新生成的活动端口，如图3（a）所示；C2是新增加的子系统的输出端口连接到当前活动端口，其输入端口连接到之前的活动端口，如图3（b）所示；C3是新增加的子系统的输出端口连接到当前活动端口，其输入端口连接到整个系统的输入端口。在本指令中，添加到现有模型的最后一个子系统的输出是整个模型的输出，如图3（c）所示。若连接方式为C1，新活动端口的值是其上一个活动端口的值加上1；若连接方式为C2或C3，则活动端口的值保持不变。

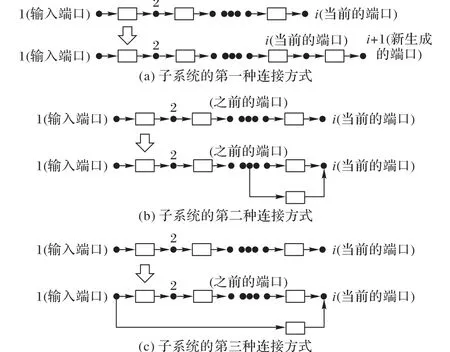
图3 子系统的三种连接方式Fig.3 Three connection modes of subsystems

2.2.3 自适应模型的生成

在AMECoDEs算法的初始过程中，指令按规则随机生成，每条指令可构造一个完整的自适应系统模型。演化开始后，系统的输入端口设置为端口1，从端口1 开始，按照指令逐一添加子系统，形成一个完整的无反馈的非线性系统。

例如，当子系统的数目S= 5 时，其信息如表1 所示，其对应的系统构造如图4所示。

表1 子系统数目为5时的系统信息Tab. 1 System information when number of subsystems is 5

图4 中，箭头是信号流的方向；x（n）和y（n）分别是系统的输入端口和输出端口。在算法初始化之后，自适应滤波模型在AMECoDEs 算法作用下进行循环的迭代优化，即通过不断的变异、交叉、选择操作和移位机制来更新种群，以找到全局最优解，即最优的系统结构和参数。

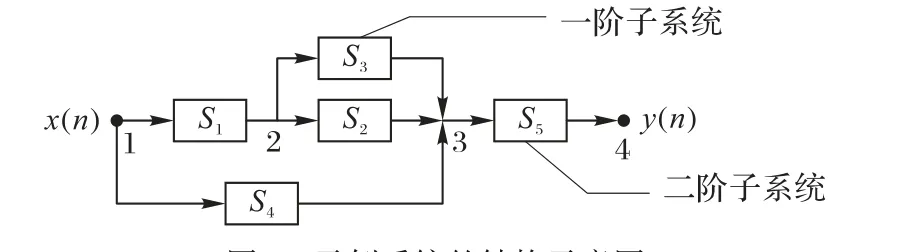
图4 示例系统的结构示意图Fig. 4 Schematic diagram of example system

2.3 收敛性评价指标

本文将非线性系统的辨识作为一个优化问题来处理。根据均方误差（Mean Square Error，MSE）、归一化均方误差（Normalized Mean Square Error，NMSE）和相关系数r三个指标对系统实际输出y^ (t)和期望输出y(t)的预测误差ε进行了收敛分析，如式（9）～（12）所示，适应值（Fitness）的计算公式如式（13）所示。

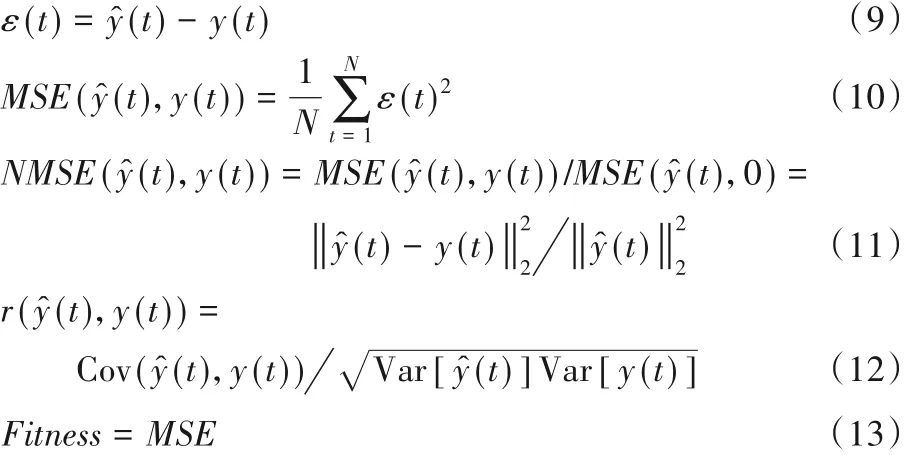
3 实验结果与分析

对5个非线性对象进行辨识，包括4个假设为未知的非线性函数和1 个实际的液体饱和蒸汽热交换系统。每一类实验均进行了100 组，且每一组进行了10 000 次迭代演化。实验结果均为100 组中选出的最优结果。辨识对象1～5 的子系统个数均设为15。

3.1 辨识对象1

辨识对象1的系统函数［20］如下所示：

其中：yp(k)是系统的输出；u(k)是系统的输入，u(k)∈［-2，2］。辨识模型可简化成如下形式：

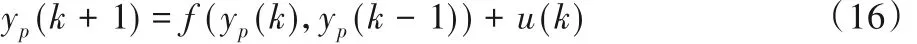
图5（a）比较了六种算法（包括AMECoDEs、粒子群优化（Particle Swarm Optimization，PSO）、DE、遗传算法（GA）、一种改进的多种群集成差分进化算法（IMPEDE）和基于成功父选择框架的差分进化算法（DESPS））的适应值迭代曲线，其中AMECoDEs算法具有最小的适应值。表2中，AMECoDEs算法的 MSE 和 NMSE 分别为 0.084 825 和 0.005 634，也优于其他五种算法。此外，AMECoDEs 算法的r为0.995 688，十分接近于1，这意味着非线性系统的绝大部分信息被自适应滤波模型成功提取，从图5（b）中的拟合曲线亦可看出。因此，本示例中，基于AMECoDEs算法的SSAF的性能最优。

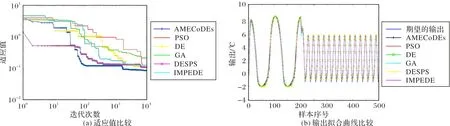
图5 辨识对象1中六种算法的性能比较Fig.5 Performance comparison of six algorithms on identification object 1

SSAF 对于本辨识对象的最优系统结构如图6 所示，其中S1、S2、S3、S5、S6、S8、S9、S10、S11、S12、S13和S14是二阶子系统，而S4、S7和S15是一阶子系统。

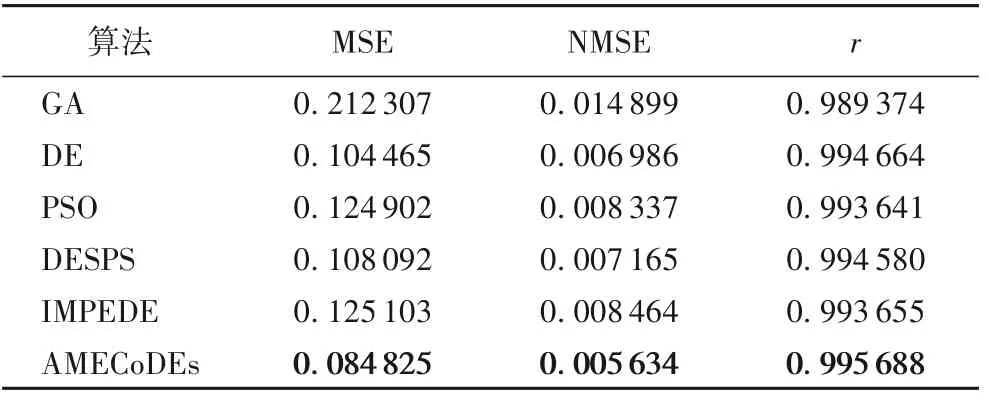
表2 辨识对象1中六种算法的收敛结果比较Tab. 2 Comparison of convergence results of six algorithms on identification object 1

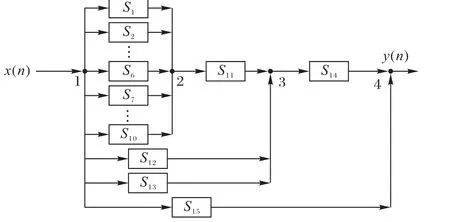
图6 辨识对象1基于AMECoDEs算法的SSAF最优结构示意图Fig. 6 Schematic diagram of optimal structure of SSAF designed by AMECoDEs algorithm for identification object 1

3.2 辨识对象2

本辨识对象的系统函数［21］如下所示：

其 中 ：a1=Yp(k)，a2=Yp(k- 1)，a3=Yp(k- 2)，a4=x(k)，a5=x(k- 1)；F表示非线性函数，如式（18）所示。

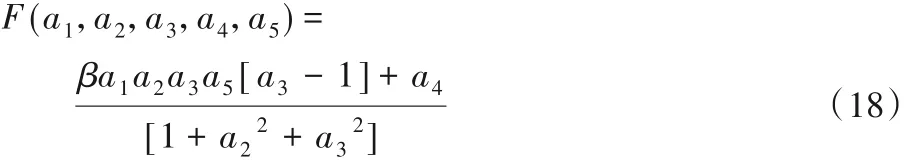
其中：β= 1，系统输入x(k)为sin(2πk/25)。

如图 7 和表 3 所示，由 AMECoDEs 算法设计的 SSAF 的适应值最小，拟合性能和收敛性优于其他五种最新算法。

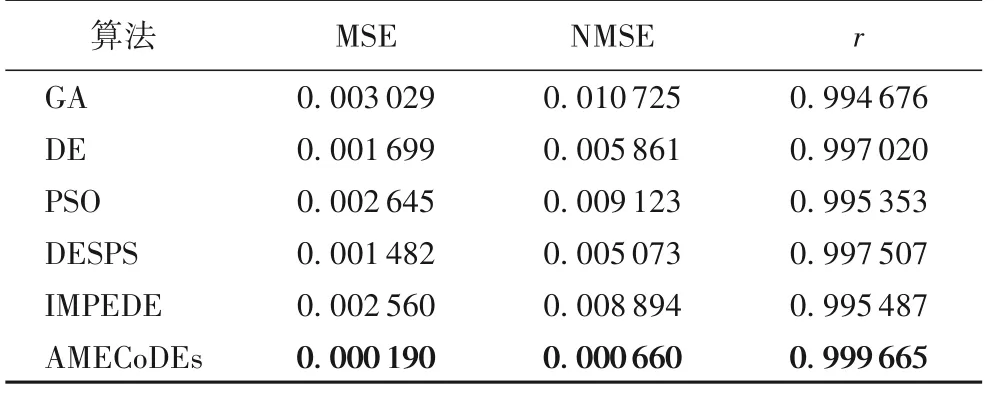
表3 辨识对象2中六种算法的收敛结果比较Tab. 3 Comparison of convergence results of six algorithms on identification object 2

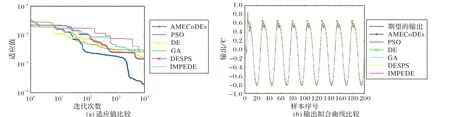
图7 辨识对象2中六种算法的性能比较Fig.7 Performance comparison of six algorithms on identification object 2

SSAF 的最优结构如图 8 所示，其中S1、S2、S3、S6、S7、S8、S12和S15是二阶子系统，S4、S5、S9、S10、S11、S13和S14是一阶子系统。

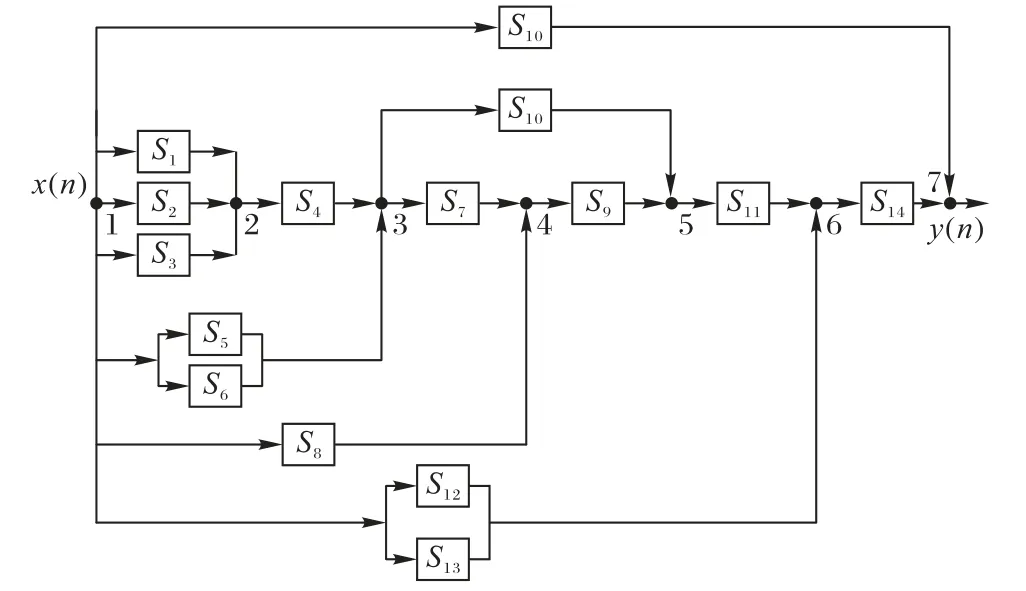
图8 辨识对象2基于AMECoDEs算法的SSAF最优结构示意图Fig. 8 Schematic diagram of optimal structure of SSAF designed by AMECoDEs algorithm for identification object 2

3.3 辨识对象3

辨识对象3的系统函数［21］如下所示：

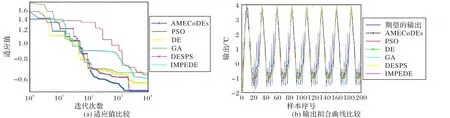
图9 辨识对象3中六种算法的性能比较Fig.9 Performance comparison of six algorithms on identification object 3

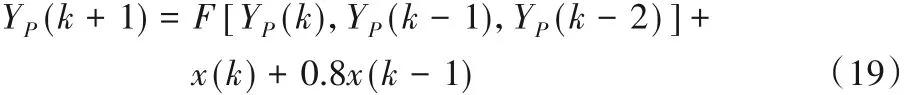
未知函数F如下所示：

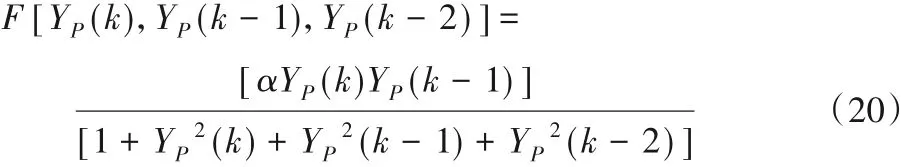
其中：α= 5，系统输入x(k)为sin(2πk/25)。

在本示例中，由DESPS设计的SSAF的综合性能在六种算法中最优。然而，如图9（a）所示，AMECoDE 的最小适应值与DEPSP 十分接近。六种算法的输出拟合曲线如图9（b）所示。表 4 中，AMECoDE 的 MSE、NMSE 和r三个指标值与 DEPSPS亦十分接近。因此，AMECoDEs 算法设计的SSAF 的综合性能与DESPS接近，在六种算法中综合性能居第二。

本示例中，SSAF 的最优结构如图10 所示。其中S9、S13和S14是二阶子系统，而S1、S2、S3、S4、S5、S6、S7、S8、S10、S11、S12和S15是一阶子系统。

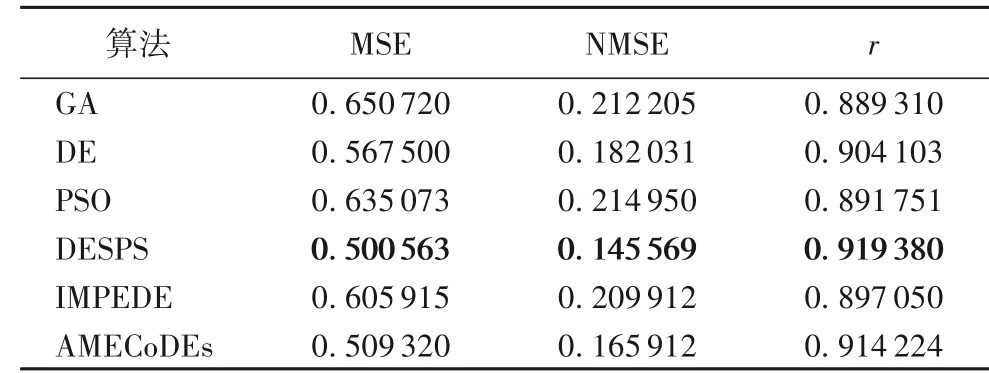
表4 辨识对象3中六种算法的收敛结果比较Tab. 4 Comparison of convergence results of six algorithms on identification object three

3.4 辨识对象4

辨识对象4的系统函数［21］如下所示：

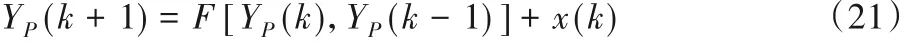
未知函数F如下所示：

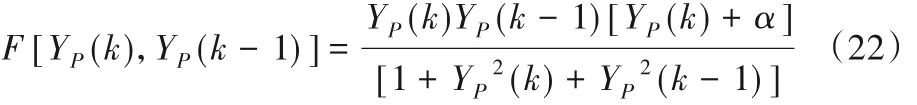
其中α值为2.5，系统输入为：

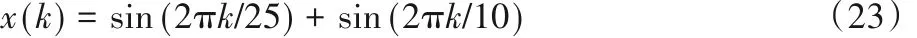
如图11 和表5 所示的仿真结果表明，由AMECoDEs 算法设计的SSAF成功地提取了非线性示例的信息，综合性能优于其他五种算法。

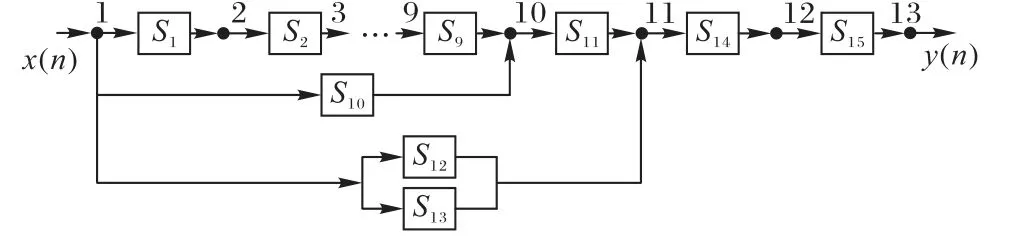
图10 辨识对象3基于DESPS算法的SSAF最优结构示意图Fig. 10 Schematic diagram of optimal structure of SSAF designed by DESPS for identification object 3

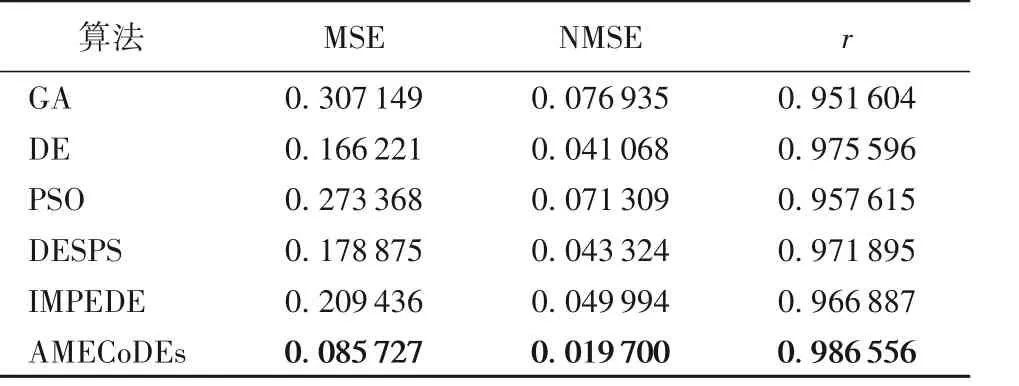
表5 辨识对象4中六种算法的收敛结果比较Tab. 5 Comparison of convergence results of six algorithms on identification object 4

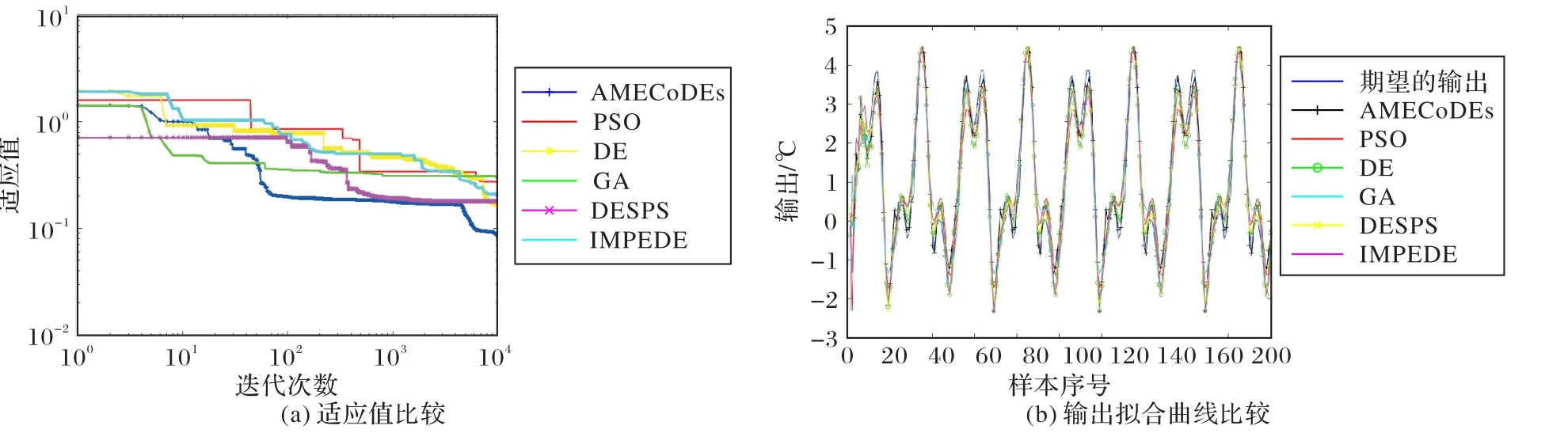
图11 辨识对象4中六种算法的性能比较Fig.11 Performance comparison of six algorithms on identification object 4

SSAF 的最优结构如图 12 所示，其中S1、S2、S3、S4、S8、S11、S12、S14和S15是二阶子系统，而S5、S6、S7、S9、S10和S13是一阶子系统。

图12 辨识对象4基于AMECoDEs算法的SSAF最优结构示意图Fig. 12 Schematic diagram of optimal structure of SSAF designed by AMECoDEs algorithm for identification object 4

3.5 辨识对象5

辨识对象5 是一个实际的液体饱和蒸汽热交换系统。液体饱和蒸汽热交换过程是非线性控制设计的重要基准（Daisy 97-002［17］），它具有非最小相位特性。该系统换热过程中，水通过铜管由加压饱和蒸汽加热，输入变量是液体流量、蒸汽温度和入口液体温度；输出变量是出口液体温度。在本实验中，蒸汽温度和入口液体温度与它们的名义值保持不变。该系统可以看作是单输入单输出（Single Input Single Output，SISO）模型。此基准中有3 200个样本，采样时间为1 s。

从辨识对象1～4 的实验结果可以看出，使用AMECoDEs算法设计的SSAF 辨识精度高、收敛速度快，综合性能优于其他五种算法。因此本实例中选用AMECoDEs算法训练基于子系统的结构自适应滤波模型（Subsystem-based structural adaptive filtering method using AMECoDEs， SSAFAMECoDEs）。辨识结果如图13所示，绝大部分非线性信息被SSAF以较高的精度成功提取。

SSAF 的最优结构如图 14 所示，其中S2，S3，S4，S5，S6，S10，S11，S13和S15是二阶子系统，而S1，S7，S8，S9，S12和S14是一阶子系统。子系统取不同非线性函数时的适应值比较如图15所示。

在 表 6 中 ，SSAF-AMECoDEs 的 MSE 及 NMSE 分 别 为0.038 323 和0.000 04，均小于聚焦时滞递归神经网络（Focused Time Lagged Recurrent Neural Network，FTLRNN）和多层感知机神经网络（Multi-Layer Perceptron Neural Network，MLPNN）相应的值；并且 SSAF-AMECoDEs 的r与 1 最为接近。此外，SSAF所用参数的数量少于120，仅为两种神经网络所用的参数数量的1/10，且SSAF-AMECoDEs 的适应值精度比FTLRNN提高了7%。由图15可以看出，在取不同的非线性函数时，LeakyRelu 函数在初始迭代时表现较优，在后续迭代过程中逐渐被Sigmoid函数超越。

综上，由AMECoDEs 算法设计的自适应滤波方法具有良好的非线性系统辨识和收敛性能。

图13 AMECoDEs算法对辨识对象5的输出拟合曲线与实际输出比较Fig. 13 Comparison of output fitting curves between AMECoDEs and reality for identification object 5

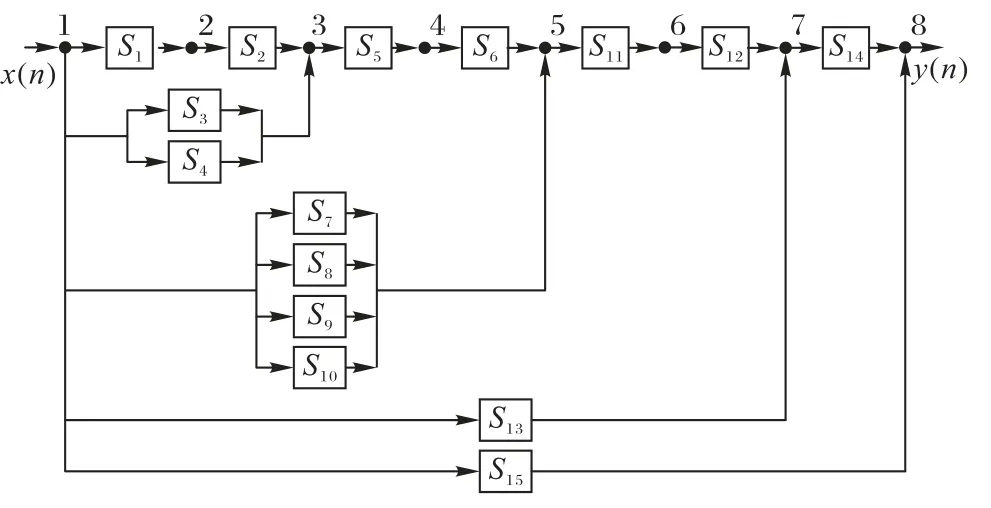
图14 辨识对象5基于AMECoDEs算法的SSAF最优结构示意图Fig. 14 Schematic diagram of optimal structure of SSAF designed by AMECoDEs algorithm for identification object 5

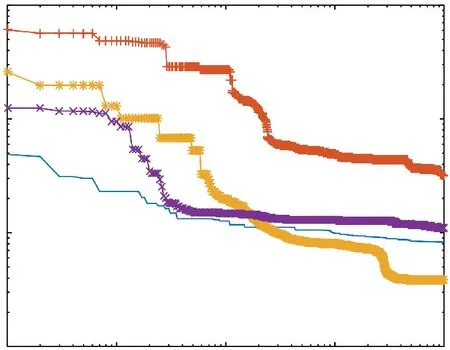
图15 辨识对象5在不同非线性函数下的适应值比较Fig. 15 Comparison of itness under different nonlinear functions for identification object 5

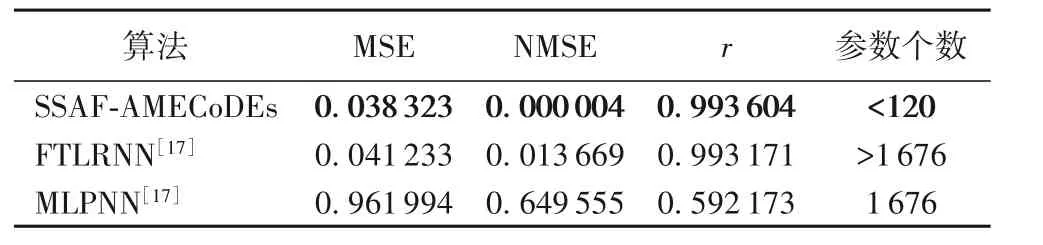
表6 SSAF-AMECoDEs和两种神经网络的收敛结果比较Tab. 6 Comparison of convergence results between SSAF-AMECoDEs and two neural networks

4 结语

本文提出了一种基于子系统的结构自适应滤波模型，该模型由子系统随机级联而成，而子系统由低阶的IIR 数字滤波器和静态非线性函数组成，无反馈的连接机制保证了模型的有效性。六种演化算法被用于自适应模型的训练和进化，对4 个非线性示例和1 个实际数据集进行了辨识和收敛性分析，仿真结果表明，基于AMECoDEs算法的结构自适应滤波模型可成功提取复杂系统的非线性信息，收敛性能优异，辨识精度高。此外，我们还将继续探讨对自适应模型的优化以及对算法的改进。