基于PSD的非均匀激光光斑中心定位研究
2020-09-03张鹏程杨海马任文佳
张鹏程,刘 瑾,杨海马,余 洛,任文佳,梁 坤
(1.上海工程技术大学电子电气工程学院,上海 201620;2.上海理工大学光电信息与计算机工程学院,上海 200093)
1 引 言
近年来,随着半导体激光器的单色性、方向性、能量集中性等性能的提高,通过激光进行定位、测量位移的光学非接触测量技术在空间光通信、工业检测、激光准直、目标跟踪等领域得到了广泛应用[1]。激光束的位置往往由其投射至探测器上的光斑中心位置确定,激光光斑中心能否准确定位直接决定了测量精度的高低[2]。传统的方法通过高帧频CCD采集光斑图像,利用灰度重心法[3]、圆心拟合法[4]、高斯分布拟合法[5]、Hough变换法[6]等进行图像处理确定光斑中心位置,但上述算法在定位精度、计算复杂度和鲁棒性方面都存在一些不足。灰度重心法易受到光斑形状与灰度值的均匀性的影响;圆心拟合法对光斑的完整性要求高;高斯拟合法和Hough变换法计算量大、实时性差。尤其针对非理想圆轮廓、非标准高斯分布的非均匀激光光斑的中心定位方法研究较少。
基于上述分析,本文提出了一种基于PSD的光斑中心定位方法并设计了检测系统。PSD的信号处理简单、位置分辨率高、光谱响应宽及测量连续性好,广泛应用于非接触测量领域[7-8]。尤其PSD 探测到的是光斑能量重心的位置坐标,与光斑尺寸的大小、能量分布的情况无关[9]。此外,PSD的非线性校正技术发展相对成熟,通过人工神经网络[10]或多项式插值[11]等优化方法可达到较高的定位精度。通过对PSD光敏面上连续旋转激光的重心轨迹处理,获取光斑的中心坐标,实现激光束的中心定位。结果表明,本文提出的基于PSD的光斑定位方法相较于CCD避免了图像处理的过程、可连续测量,且定位精度高,为解决非均匀分布光斑的中心定位问题提出了一种新思路。
2 PSD定位原理及信号处理
2.1 PSD原理模型
PSD是一种基于半导体横向光电效应的光斑位置探测器,其数学模型可以通过Lucovsky方程[12]来描述。如图1(a)所示,采用的二维枕形PSD基本结构为一设有弧形电极的面状光敏面,其边缘对称引出四个阳极,同时背面设有一个公共阴极,用于工作时施加反向偏置电压以获得更理想的线性度[13]。PSD的等效电路图1(b)由面电极电阻RP、横流源IP、理想二极管D、结电容CJ、并联电阻RSh组成[14]。
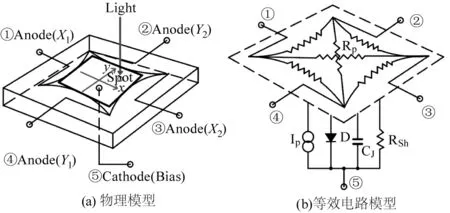
图1 枕形二维PSD结构模型
当激光投射至光敏面上形成光斑时,光能转换为结间流动的光电流,四个电极的电流强度与光斑能量重心的位置存在唯一对应关系,以光敏表面中心为原点的坐标方程为[15]:
(1)
式中,UX1,UX2,UY1和UY2为四个电极的光电流转换后的电压值;LX和LY为PSD方形光敏面的尺寸;κ为非线性校正系数[15]。
2.2 PSD信号处理方案
PSD作为一种光电转换器件,光源投射至探测器表面后激发的信号为μA级的光生电流,需要通过前置放大电路将微弱电流信号转换为V级的电压信号进行采集[16]。因此,本文提出了图2中的二维PSD的信号处理方案。

图2 二维PSD信号处理方案
由运放和反馈电阻构成的电流电压转换(I/V)电路,通过调节反馈电阻来控制电路增益。数据采集卡对放大后的光电压模拟量进行AD采集,经过数字量运算获得光斑位置轨迹数据,最后通过中心定位算法处理获得光斑中心坐标。此方案未用模拟电路对位置坐标进行加法与除法运算,一定程度上抑制了因模拟器件的噪声和温漂特性造成的信号干扰。
3 非均匀激光光斑中心定位
3.1 激光光斑模式
当激光处在光学谐振腔内振荡的过程中,光束横截面上的稳定分布称为激光束的横向模式(横模)[17]。以激光束发散的正方向作为Z轴建立欧式三维坐标系,取垂直于Z轴的平面定义X和Y轴。理想激光束横模的能量分布为二维高斯分布,投射到PSD光敏表面的光斑能量密度函数为:
(2)

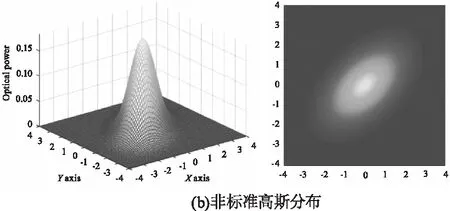
图3 PSD光敏面上呈高斯分布的光斑模型
3.2 光斑中心定位
当激光束在空气中传播,空气中的微粒会造成其散射、反射、和折射等情况,使得激光束的能量密度分布发生改变,最终导致光敏面上的光斑往往是能量非均匀、形状非完整的。本文依据PSD定位光斑重心位置不受限其形状、能量分布对的特点[9],提出了图4中的旋转激光光斑中心定位方法。
半导体激光器投射激光至PSD光敏面形成光斑,旋转激光装置逆时针进行旋转,获得连续的光斑重心轨迹坐标(xi,yi)(i=1,2,…,n)。由于为定轴心旋转方式,通过对轨迹的圆曲线进行拟合得到圆心(xc,yc)定义为此光斑的中心。

图4 旋转激光光斑中心定位原理
考虑到定位系统的重要指标-响应速度与处理数据算法的复杂度,可采取基于代数拟合的Kasa算法。传统的圆曲线拟合方法的目标函数为[18]:
(3)
(4)
(5)
通过求F对B,C,D的偏导数,得到一个线性方程组:
吸收塔主要承受自重、内压、风荷载、地震荷载、浆液荷载以及塔内件荷载作用。有限元模型中荷载的施加方式如下:
(6)
为简化计算,可改写为矩阵形式:
(7)
解决极小值问题后得到圆曲线的标准方程:
(8)
式中,(-B/2,-C/2)为圆心位置(xc,yc);[(B2+C2-4D)/4]1/2为圆曲线半径r。拟合出的圆心即为光斑中心位置。定义轨迹中任意数据点相对于圆曲线半径方向的变化量为:
εi=(xi-xc)2+(yi-yc)2-r2
(9)
则定义圆度值(表示拟合圆的标准程度)为:
Re=max{εi}-min{εi}
(10)
4 PSD光斑中心检测系统
根据文中提出的光斑中心定位方法,设计了图5中的旋转激光光斑检测系统。系统装置由日本滨松光子的C10443-02二维枕形PSD、基于光斑尺寸与功率可调的650 nm半导体激光器和空心轴步进电机制作的旋转激光装置、NI的USB6009数据采集卡和精密的数控平移台组成。采用的PSD有效光敏面尺寸9 mm×9 mm,响应时间2 μs,光谱响应范围320 nm~1100 nm。数控平台三轴可移动范围200 mm,单轴最小位移为0.01 mm,精度为0.001 mm。旋转激光装置采用细分技术和串口协议进行控制,最小旋转角度0.1°,精度为0.05°。数据采集卡具有8个14位分辨率的模拟量输入通道,按照图2中的信号处理方案进行位置电压信号采集。
旋转激光装置通过光学夹具安装在数控平移台上。PSD固定于光学精密手调二维平移台上,通过调整平移动台实现系统的高精度对中。在系统使用前,需提前打开激光器静置一段时间以获得稳定的光斑。此外,整个检测系统在弱光环境下进行工作。

图5 旋转激光光斑检测系统
5 实验与分析
5.1 旋转光斑模式
激光束在旋转的过程中光斑模式的变化情况会对PSD的位置探测产生影响,因此需要对旋转光斑的模式进行分析。首先对旋转过程中的光斑图像进行采集。如图6所示,观察到旋转光斑能量分布不均匀、形状不理想但模式无明显变化。

图6 旋转激光光斑图像
此外,通过光功率计配合扩束透镜和平移台对光斑在正交方向上的能量分布进行测量,如图7所示。

图7 旋转激光能量分布实验
由图8可知,在X和Y方向上的能量均不符合理想的激光的高斯分布,且二者之间的差异仍然是明显的,因此不可轻易地将光斑的能量重心假设为光斑的中心。


图8 光斑正交方向上能量分布
综上所述,在旋转过程中光斑的模式并未发生明显改变,对PSD定位影响较小且光斑的能量分布不均匀程度较大。
5.2 光斑中心轨迹定位
在实验过程中,首先调整数控位移平台,使激光束投射到PSD光敏面的中心区域。然后,再对固定PSD的二维位移平台进行微调,直到由电压信号计算出的位置坐标与原点重合。最后采用螺旋矩形法对9 mm×9 mm的有效区域进行扫描,扫描步长为1 mm,采样频率为200 Hz。在每个采样点处,控制旋转激光装置逆时针旋转三次,并对PSD的电极信号进行处理和记录。在对所有位置完成采样后,可得到81组轨迹数据,并通过平均值法来减小测量误差。完整的扫描轨迹如图9所示,图中将光斑重心旋转的初始位置用点进行标注,并用直线平滑连接。
当光斑在PSD光敏面的边界区域旋转时,重心位置可能会超出有效探测范围,导致左边界和上边界的轨迹出现明显畸变。该边缘畸变不能通过非线性校正来优化,但可通过选取较小尺寸的光斑或牺牲一定的边界探测范围来提高整体定位精度。
根据Kasa方法来处理每组光斑轨迹数据,结果如图10所示,光斑中心位置用点标注并用直线连接即移动轨迹。为验证定位精度,对定位前后位置坐标理论上满足y=-x的点进行线性回归分析,详细坐标由表1列出。
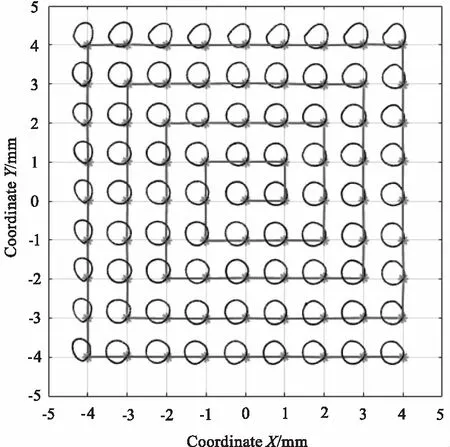
图9 PSD光敏面上光斑重心扫描轨迹

图10 PSD光敏面上光斑中心移动轨迹
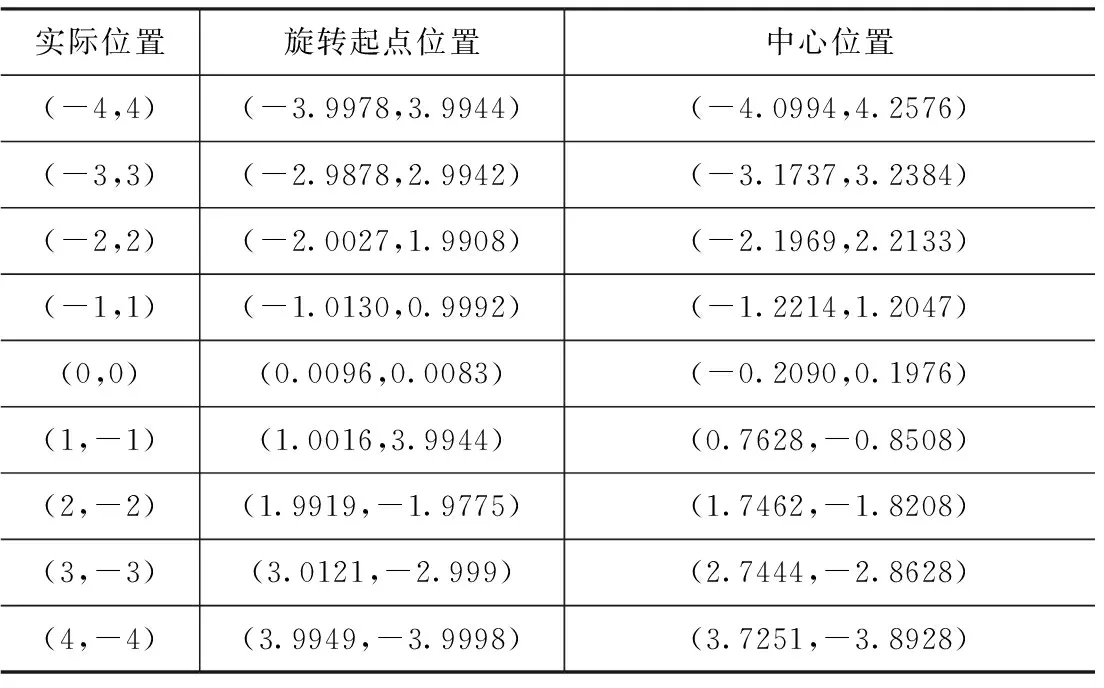
表1 线性回归分析坐标数据(单位:mm)
建立的一元线性回归模型为:
(11)
模型的RMSE(均方根误差)分别为0.01293和0.02775,表明回归方程真实可靠。原始轨迹模型和光斑中心位置模型的线性相关系数均与理想值-1十分接近,证明PSD的位置线性度较好且移动光斑中心定位精度较高。
图11从81组轨迹数据的处理结果对Kasa方法的精度进行了分析。图中圆的标号与之前的扫描顺序相对应,标号1~49为7 mm×7 mm范围的轨迹,50~81为光敏面边界区域轨迹。拟合误差符合随着靠近边界区域逐渐增加的趋势,且误差在边缘区域即从标号50开始激增。但在标号1~49的范围内,拟合半径和拟合圆的理想度分别在0.01 mm和0.002 mm范围内波动,仍有较高的拟合精度。
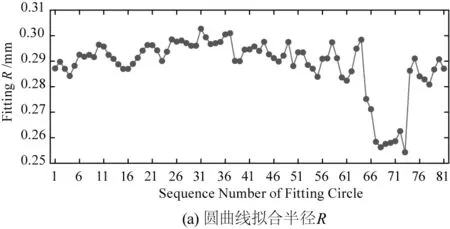

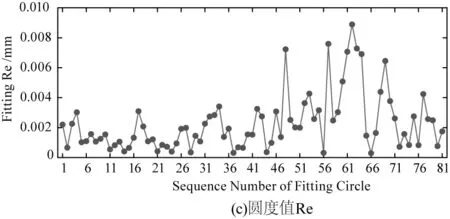
图11 Kasa方法的圆拟合精度
6 结 论
基于二维PSD的激光光斑中心定位方法相比于传统CCD方法对光斑的能量分布与轮廓形状要求低、无需图像处理的步骤,且位置探测精度高、响应速度快、算法复杂度低。通过Kasa代数算法处理旋转光斑重心的轨迹,在7 mm×7 mm光敏面内拟合半径和圆度值的标准差分别为0.0042 mm和0.0012 mm,证明该方法具有较好的鲁棒性与精度。激光光斑中心定位的线性度为-1.036、位置分辨率为0.1 μm,精准定位了光斑中心的移动轨迹,为非均匀光斑的高精度定位提供了一种新思路。
