基于五点法的单幅光学干涉条纹相位提取

郗洪柱,孔德仁,王伟魁,乐贵高

(1.航天长征火箭技术有限公司传感器部,北京 100076；2.南京理工大学机械工程学院,江苏 南京 210094)

1 引 言

非接触式光学测量通常利用光干涉原理测量各种物体的参数,如材料折射率、光学元件特征参数、薄膜厚度、微位移以及痕量气体浓度等[1-6],具有很高的测试灵敏度及准确度。在动态干涉测量中,需要通过干涉条纹相位信息获取反应物体状态的某一物理量。目前干涉条纹相位提取算法较多,根据提取相位所需干涉条纹图幅数,分为单幅和多幅干涉条纹相位提取算法。单幅干涉条纹相位提取算法仅需一幅干涉条纹图即可提取相位信息,主要应用于动态和对实时性要求较高的测量上,包括同步法、锁相法、傅里叶变换法、正则化相位跟踪法、希尔伯特变换、遗传算法和小波变换[7-10]等；多幅干涉条纹相位提取算法需要多幅干涉条纹图才能得到一次相位信息,主要应用于静态和对实时性要求不高的测量上,主要指相移法,包括Hariharan五步算法、Carre算法和最小二乘法等[11]。相移法操作过程复杂,且对相移或空间位置精度要求较高[12]；傅里叶变换法及希尔伯特变换法等动态测量算法复杂度较高,存储和参与运算的数据量大,在可编程器件上占用资源较多,运算速度受到一定影响。

本文构建的中心五点相位提取算法仅需一幅干涉条纹,利用线阵干涉条纹中五个特征点光强计算其相位,即最大点、最大点两侧最近的极小点、以及上述三点间两中间点。固定上述五个特征点位置,获取新的干涉条纹对应五点光强,重复上述计算,即可获取连续变化的相位。同希尔伯特相位提取算法比,相位提取过程数据位数扩展少,避免了截断误差；同FFT法比,不涉及乘法器,无需存储大量数据；此外,算法无需去除干涉条纹直流分量,简化了计算量。相位求解精度高,计算过程耗费资源更少,速度更快,实时性能更佳,便于更广泛应用。

2 算法原理

分别用I(x,y)、Idc(x,y)、Iac(x,y)、φ1(x,y)和φ2(x,y)表示像素坐标(x,y)处光强度、光强直流分量、交流分量、测量光束相位和参考光束相位,则干涉光强公式为:

I(x,y)=Idc(x,y)+Iac(x,y)cos[φ1(x,y)-φ2(x,y)]

(1)

为减小相移误差的影响,Hariharan五步法需要五幅同一像素处相位相差π/2的干涉条纹作为计算对象,通常选择测量光束和参考光束间相位差Δφ(x,y)=φ1(x,y)-φ2(x,y)为0、π/2、π、3π/2和2π。五步法求测量相位的计算公式为[13]:

(2)

上述方法需同一点处连续五幅相位相差π/2的干涉条纹光强,需控制获取干涉条纹时机,定位特征点光强值才能得到测量光束相位,硬件成本高,限制了其在实时干涉测量领域的应用。考虑从单幅干涉条纹中获取相位相差π/2的五点光强,即:

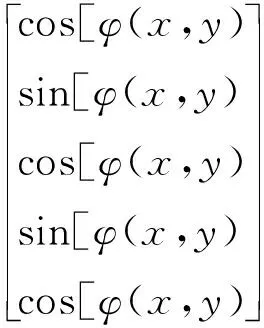
(3)

在单幅干涉条纹中寻找五点求测量光束相位,各点相位依次相差π/2。考虑到干涉条纹光强的余弦特性,为提高分辨率和检测精度,选择任一幅干涉条纹最大点处作为相位π点,选取π点左右两个最近的极小值处分别作为相位0和2π点。为保证取点对称性,π/2点在0点和π点中间取,3π/2点在π点和2π点中间取。由式(3)可明显得到关于I2和I4的如下约束:

I2+I4=I1+I3

(4)

在取π/2和3π/2点时使对应点光强值尽量满足式(4)。

由于光源的非单色性使干涉条纹光强最高处同一方向依次分布的亮条纹宽度变大,最大光强变小,最终在数个明暗条纹后,明暗条纹光强一致,可见度为零。另外由于干涉条纹相位存在畸变[15],受物体表面特征和投射角变化的影响,条纹的灰度分布也会有不同程度的非对称退化[16],最大值左右两侧最近的两个极小值并不相同(即I1≠I5),故在单幅干涉条纹上,各像素处的Idc(x,y)和Iac(x,y)并不完全一致,视为基本不变时将会引入误差。将五点处直流分量Idc(x,y)视为常量,仅考虑不同位置处交流分量Iac(x,y)的不一致性,定义误差系数c为相位解算结果的正切值同真值的正切值之差后除以真值的正切值,即:

(5)

采用非对称参数a作为误差系数c的评价指标,单位为像素。分别用mL、mR和max表示中心五点法中左极小值、右极小值和最大值像素位置,则非对称参数定义为:

(6)

非对称参数a大于零,干涉条纹主峰位置偏左,误差系数c大于零,相位解算结果偏大；非对称参数a小于零,干涉条纹主峰位置偏右,误差系数c小于零,相位解算结果偏小；非对称参数a绝对值越大,相位解算结果偏差越大。当每幅干涉条纹非对称参数a固定时,误差系数c固定,根据式(5)可知,x固定不变,进一步,为方便分析,可固定Iac2、Iac3和Iac1,即认为I1、I2和I3处于余弦函数上,根据式(4)即可确定I4的值,I5的选取受“最大值右侧最近极小值”约束,按照理想余弦函数,则I5=I1,但由于实际干涉条纹非对称退化现象,两者并不相等。非对称退化是系统固有现象,可视为系统误差,因此在这种情况下,相位解算误差变为系统误差,通过后续标定可一定程度上消除该误差的影响,但会使相位结果与待测物理量间的关系变复杂。

3 数值模拟

利用计算机产生512像素点线阵干涉条纹,干涉条纹携带的相位满足下式:

(7)

干涉条纹每周期12个像素点,直流偏置为0.6,幅值为0.5,如式(8)所示,使用时对其中段加海明窗,前后两段减小窗函数并抑制原始信号。

(8)

图1为数值模拟结果。图1(a)为不带噪声的干涉条纹模拟图,含有256幅线阵512点干涉条纹,每幅条纹携带一个式(7)所述初始相位信息,加窗使得图1(a)中间几条干涉条纹明显,两端干涉条纹很弱,满足实际线阵干涉条纹要求；为了更好地分析中心五点法效果,对模拟移相干涉法(PSI)、快速傅里叶变换(FFT)法、中心五点法和两次希尔伯特变换法的相位解算结果绘制于图1(b)中。由图1(b)可知,中心五点法相位解算结果最接近原始相位变化,两者差值平方和(Sum-of-Squared Differences,SSD)为0.1114,如表1所示,在三者中最小；FFT法相比两次希尔伯特变换法,结果更接近原始相位变化,前者SSD为13.1001,明显小于后者SSD值107.9121；后两种算法均在连续相位解算任务的初始数十帧干涉条纹中与原始相位相差较小,随着帧数增加,两次希尔伯特变换法相位解算结果偏离原始相位值变大。

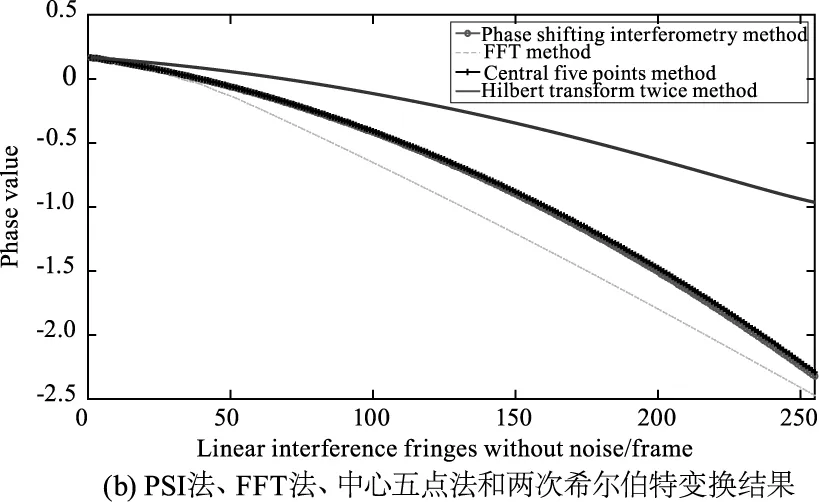
图1 不带噪声数值模拟结果

表1 不带噪声时三种方法分别与移相干涉法对应点差值平方和

对图1(a)中不带噪声的干涉条纹施加对应点数的高斯噪声,噪声均值为0,方差为每帧干涉条纹均值。图2(a)为带高斯噪声的干涉条纹模拟图,图2(b)为上述几种方法的相位处理结果。可知,中心五点法和两次希尔伯特变换法受噪声影响明显,相位解算结果均出现波动,但两次希尔伯特变换法波动更大,FFT法受噪声影响小。如表2所示,与表1对比可知噪声引起中心五点法和FFT法与PSI的SSD值均变大,噪声使两次希尔伯特变换法向靠近PSI结果方向波动,因此其SSD反而减小。综合来看,噪声情况下,仍然是中心五点法相位解算结果最接近原始相位变化,此外,FFT法优于两次希尔伯特变换法。

(a)带高斯噪声的干涉条纹模拟

图2 带噪声数值模拟结果

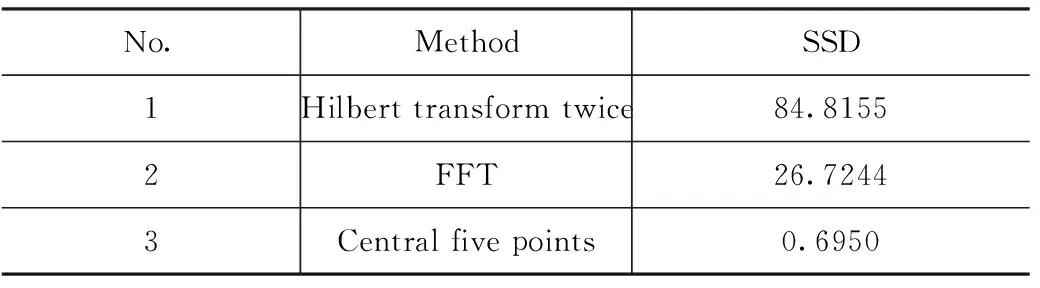
表2 带高斯噪声时三种方法分别与移相干涉法对应点差值平方和

4 实验及分析

利用FPGA实现512点CMOS图像传感器的高速驱动,并对干涉条纹高速采集和处理。干涉条纹由MEMS工艺硅悬臂梁在密闭光声腔内产生。悬臂梁振动时在CMOS图像传感器上产生相位变化的干涉条纹。实验系统主要由两块控制电路板,一组量子级联激光器及其驱动模块,一组光声池模块组成。整个系统实验平台及现场如图3(a)所示。

实验中一组干涉条纹被CMOS图像传感器转换后经采样率为4 MHz的高速AD(AD9240,14 bits)采集,平滑连线后如图3(b)所示,图中横坐标像素点对应的纵坐标像素值用圆圈标注。计算每幅干涉条纹非对称参数a,为固定值0.5,因此干涉条纹非对称现象引起的相位解算误差是系统误差,可利用标定手段一定程度上消除该误差的影响。

(a)实验平台

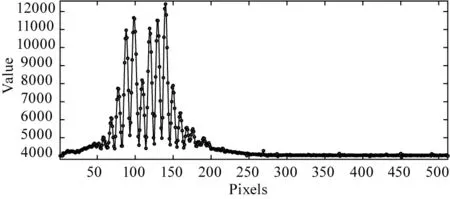
(b)线阵干涉条纹

取连续20幅干涉条纹,滤除直流分量,如图4(a)所示。利用中心五点法计算滤波前后对应各幅干涉条纹的相位,如图4(b)所示,图中“Before”为滤波前的20个相位解算结果,“After”为滤波后的20个相位解算结果,两者吻合度高,滤波前相对于滤波后相位解算平均差值为0.06 %,约为9.55×10-5个波长,误差非常小[17],可忽略。当直流分量较大,如为交流分量3倍时,滤波前后相位差值均值为3.2×10-11,亦可忽略。故而中心五点法无需滤除干涉条纹直流分量。

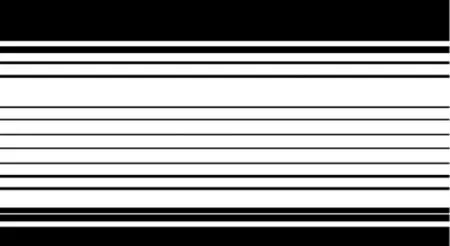
(a)去直流后干涉条纹

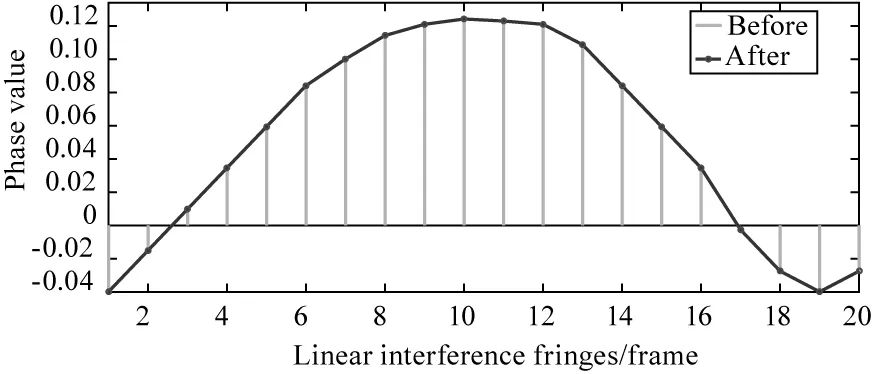
(b)干涉条纹滤波前后中心五点法相位结果

分别利用中心五点法、两次希尔伯特变换法和FFT法提取线阵干涉条纹相位信息,将两次希尔伯特变换得到的相位取反,前两种算法相位结果减去各自均值,对FFT法得到的相位结果的幅值和偏置做调整,三种算法的结果如图5所示。中心五点法和FFT法相位解算结果完全重合,上述两种方法的结果与两次希尔伯特变换法基本重合,定义峰峰值为相对分辨率,则中心五点法和FFT法相对分辨率为0.1643,希尔伯特变换法相对分辨率为0.1681,上述相对分辨率相当,前后差值占比仅约为2.26 %。

希尔伯特变换通过有限长单位冲激响应滤波器实现,经过两次希尔伯特变换,输出结果位数将会翻几倍。在除法和反正切运算中均增大了运算量,对过程和结果数据的截取还会造成计算精度下降。FFT法通过调用Xilinx的“Fast Fourier Transform”核,按照512点,流水线模式,结果四舍五入,自然序列输出方式配置实现所需功能,占用较多乘法器,流水线模式可提高运算速度,但级数越多资源占用越大。中心五点法仅是对数据做加减运算,并未增加除法和反正切运算量,不涉及乘法器的使用,在资源和运算开销上较前两者具有明显优势。

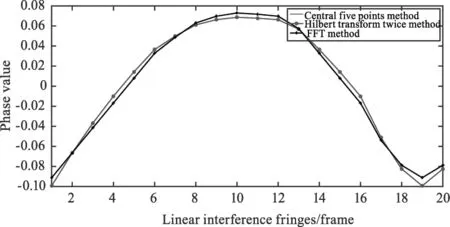
图5 中心五点法、两次希尔伯特变换法和FFT法相位

在同一FPGA平台(Xilinx公司Virtex-II系列300万门FPGA)实现中心五点法(No.1)、两次希尔伯特变换法(No.2)和FFT法(No.3),算法均包含模数芯片驱动、线阵干涉条纹图像传感器驱动及解包裹模块,资源占用见表3。FFT法中仅FFT核即消耗12个乘法器(MULT18×18),5个块随机存储器(Block RAMs)以及大约3165个总逻辑单元(Slices)。综合分析,FFT法在Block RAMs和MULT18×18上的消耗量远多于另两种；FFT法和两次希尔伯特变换法在触发器(Flip-Flop)、四输入查找表(4-LUT)以及Slices使用量上均远多于中心五点法。总体而言,中心五点法相比希尔伯特变换法和FFT法分别节省22 %和27 %的逻辑资源。

表3 三种算法逻辑资源开销

在100 MHz系统时钟下,从一幅干涉条纹采集完毕到相位解算结果输出,中心五点法消耗90个系统时钟,即900 ns；两次希尔伯特变换法消耗95个系统时钟,即950 ns；FFT法消耗512个系统时钟,即5120 ns。前两种方法时间瓶颈均在除法和反正切模块,前者消耗59个系统时钟,此外,五点数据需先从块RAM中读取,占用约19个系统时钟；后者消耗66个系统时钟。FFT法耗时最多,时间主要消耗在将干涉条纹512点数据在系统时钟下串行加载至模块中。总之,中心五点法较两次希尔伯特变换法和FFT法在运行速度上分别具有约5 %和469 %的优势。

5 结 论

基于五点相位求解算法,构建了一种快速、高精度单幅干涉条纹相位提取算法。该算法通过单幅线阵干涉条纹上最大点、最大点两侧最近极小点、以及上述三点间两中间点计算干涉条纹相位。该算法过程数据位数扩展少,不涉及乘法器,不需存储大量数据,无需去除干涉条纹直流分量,直流分量不滤除引起的相位精度误差仅为9.55×10-5λ,简化了计算量。数值模拟和实验测试结果表明,该算法同FFT法的相对分辨率一致,同两次希尔伯特变换算法有约2.26 %的区别,在FPGA平台运行速度比后两者分别快469 %和5 %,资源消耗分别节省27 %和22 %,具有相位解算精度高,运算速度快,资源开销低的优点,对单幅干涉条纹相位提取具有重要指导意义。