胶凝砂砾石材料宏细观参数及破坏模式研究

黄虎, 李坡, 霍文龙, 张献才

(华北水利水电大学,河南 郑州 450045)

胶凝砂砾石 (Cemented Sand and Gravel,CSG)材料是将水、胶凝材料、河床砂砾石或开挖废弃料等当地材料按一定比例混合,然后拌合后得到的一种新型筑坝材料。随着2004年我国首例CSG围堰的建成应用,CSG材料在水利工程中的应用也逐渐推广。贾金生等[1]于2009年提出了胶结颗粒料坝和“宜材适构”的新型筑坝理念,并推动国际大坝委员会设立了胶结颗粒料坝专业委员会,编制了胶结颗粒料坝水利行业技术标准。2014年,我国第一座永久性CSG坝工程——山西守口堡水库CSG坝开工建设。随着CSG坝理论研究的深入,我国的CSG坝正由临时工程向永久工程、低坝向高坝过渡。

目前,国内外在CSG材料的静力学特性方面取得了大量有价值的研究成果。2003年,BATMAZ S[2]结合土耳其Cindere坝进行了CSG料的强度试验研究,发现当胶凝掺量为70 kg/m3时,90 d龄期CSG料的强度可达5 MPa以上,可满足高100 m大坝的强度要求。ADL M R[3]通过对胶凝砂砾石材料进行不同围压下的三轴不排水试验得出:在高围压和低胶凝材料时,试件出现明显的膨胀;随着胶凝材料含量的增加,摩擦角的变化不大,但黏聚力变化明显。贾金生等[4]通过试验对福建街面水电站下游围堰工程的筑坝材料进行了研究,结果表明,当地天然砂砾石掺入水泥和粉煤灰各40 kg/m3后,180 d龄期CSG材料的抗压强度可达到C7.5,满足围堰的安全稳定要求。2007年,孙明权等[5]对不同胶凝掺量的CSG材料进行了三轴剪切排水试验,结果表明,CSG材料的应力-应变曲线具有明显的非线性特征及软化特征。通过对立方体试件进行抗压强度试验和劈裂试验发现[6],在静力荷载作用下,CSG材料的破坏主要是胶结面的破坏,最终的破坏是由于胶结体的断裂导致材料成为散粒体,而粗骨料本身并未发生任何形式的破损,从宏观上表现为试件的剪切断裂和压碎。蔡新等[7]通过大型三轴试验发现,胶凝堆石料的剪胀性明显,在不同围压下,材料的破坏形式也存在不同,围压越小,剪胀越明显;低围压下胶凝堆石料的骨料不会破碎,骨料间的黏结力丧失后,在剪切力的作用下骨料容易滚动和翻转,试件表现为较明显的先缩后胀;高围压下的胶凝堆石料的骨料容易破碎,也可能滑动、挤压或者填充孔隙,翻转和滚动较少。虽然国内外在CSG料力学特性方面取得了大量有价值的研究成果,但主要是对室内试验宏观现象的总结,关于其细观力学试验的研究还鲜有提及,对材料的破坏机理还有待进一步研究,进行CSG材料的细观试验研究是未来的研究方向[8]。本文在前人研究的基础上,采用宏观与细观相结合的方法,在室内试验的基础上,根据宏观力学性能探寻细观参数的变化规律,得出适合CSG材料的细观参数,通过研究揭示CSG材料的细观破坏模式,为深入研究CSG材料的力学特性和破坏机理、建立基于细观的数值分析模型提供参考和借鉴。

1 试验方案

1.1 室内试验

1.1.1 试件制备

根据胶结颗粒料筑坝技术导则(SL 678—2014),胶凝材料用量不宜低于80 kg/m3,其中水泥熟料用量不宜低于32 kg/m3,水胶比宜控制在0.7～1.3,CSG中砂率宜在18%～35%[9]。限于篇幅限制,结合已有研究成果[10-12],本文仅对一种配合比方案进行试验分析。胶凝材料采用普通硅酸盐水泥(P·O42.5)和干排F类Ⅱ级粉煤灰,含量分别为40 kg/m3和50 kg/m3;砂率为0.2;水胶比为1∶1;砂砾石材料为汝州市天然河床的开挖料,经人工筛分为粒径5～20 mm、20～40 mm的二级配天然骨料。试件为φ150 mm×300 mm的圆柱体,试件的制备采用机械和人工相结合的拌和方式,装入钢模具内，常温下放置48 h,拆模后将其置于标准养护室内养护28 d。

1.1.2 试验加载

室内试验在WAW-1000型微机控制电液伺服试验机上完成。加载速率为1 mm/min,试件破坏后停止加载,试验结束。试验中记录应力-应变关系曲线。

1.2 数值模拟试验

1.2.1 平行黏结模型

数值试验通过离散元软件PFC2D来完成。为较好地模拟CSG材料中骨料间的相互作用,颗粒间的相互作用采用平行黏结模型模拟[13],如图1所示。图1中：A、B为两个接触颗粒;xi[A]、xi[B]和xi[C]分别为颗粒A、B及黏结部分的中心坐标;R为黏结半径;L为黏结厚度;作用于颗粒A和B上的附加荷载会分配给接触弹簧和平行黏结弹簧,从而实现力和力矩的传递。虽然该模型不能完全模拟实际材料中的胶结量,但力学分析得到的胶结性状改变的结果在一定程度上反映了胶结砂砾石的力学响应趋势。

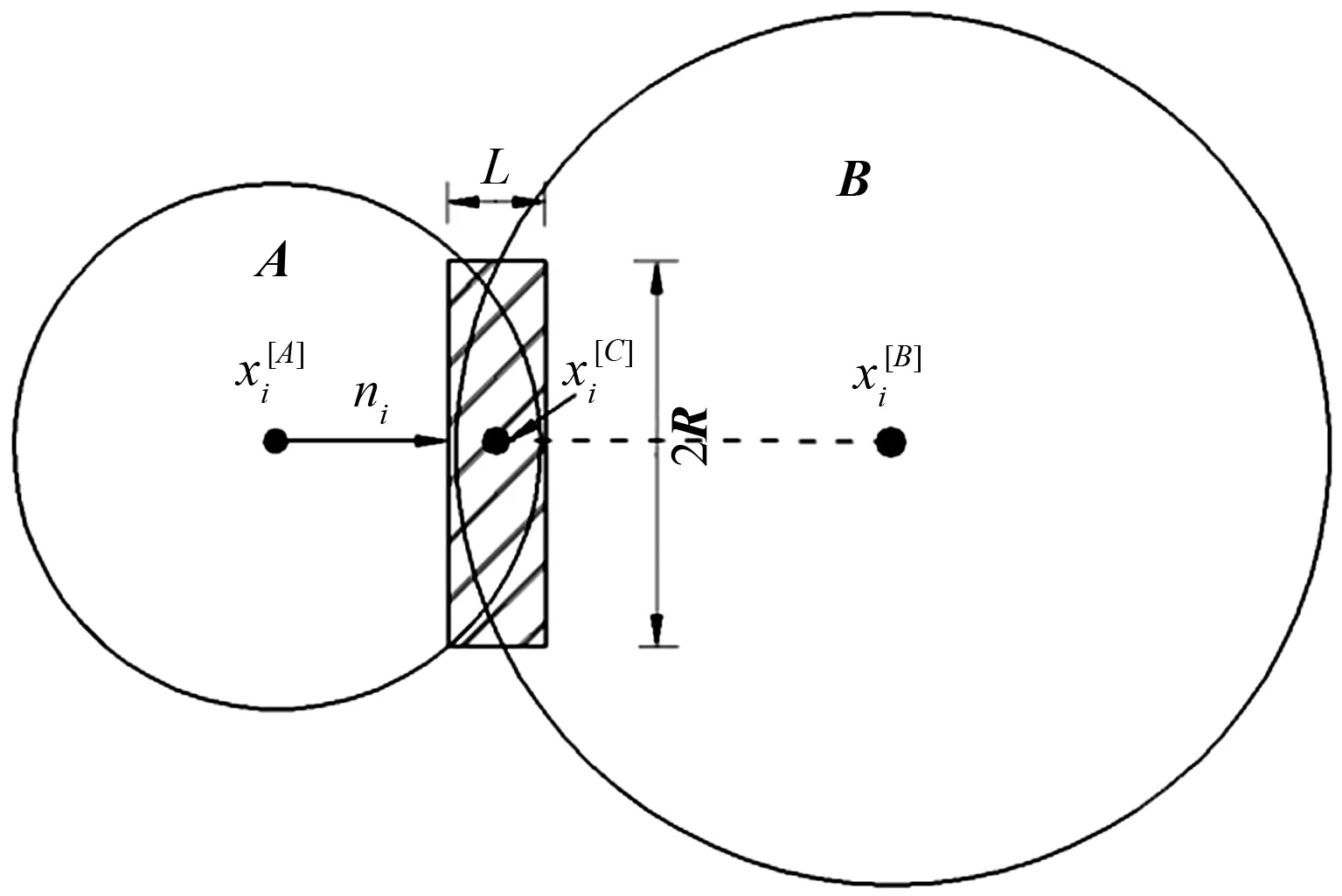
图1 平行黏结模型

1.2.2 数值模型

为保证数值模拟试验数据和室内试验数据的可比性,数值模型试件与室内试验试件保持一致,模型均高300 mm,宽150 mm。根据材料选用的砂、砾石的级配方案,试件为φ150 mm×300 mm的圆柱体;试件内骨料粒径为5～40 mm,且形状复杂不均。通过数值模型建立完全符合骨料形状的颗粒流模型是不现实的。根据文献[14]的结论,当模型高度与颗粒平均半径的比值H/r≥125时,颗粒的大小不会对各项宏观参数造成影响。本文试验中骨料颗粒的平均半径为2.25 mm,H/r=133>125,故不必考虑骨料颗粒大小对各项宏观参数的影响。在建立数值模型时,预先设定颗粒的最小半径为0.5 mm,最大半径为4 mm,然后随机生成骨料颗粒,并控制最大半径颗粒的数量。采用重力沉积法实现试样的制备,在“U”型区域内生成松散颗粒,施加重力,颗粒开始沉积;沉积完成后,设置颗粒ball的密度、局部阻尼,运算至收敛,则完成了试件数值模型的建立,如图2所示。数值模型的底部和顶部均设置为“wall”,为刚性板边界;底部“wall”采用全约束;顶部“wall”施加应变控制荷载。整个数值模拟试验通过伺服调节法控制模型的加载过程来完成。

图2 数值试验模型

2 宏、细观参数间的定量关系分析

2.1 平行黏结法向刚度对宏观参数的影响

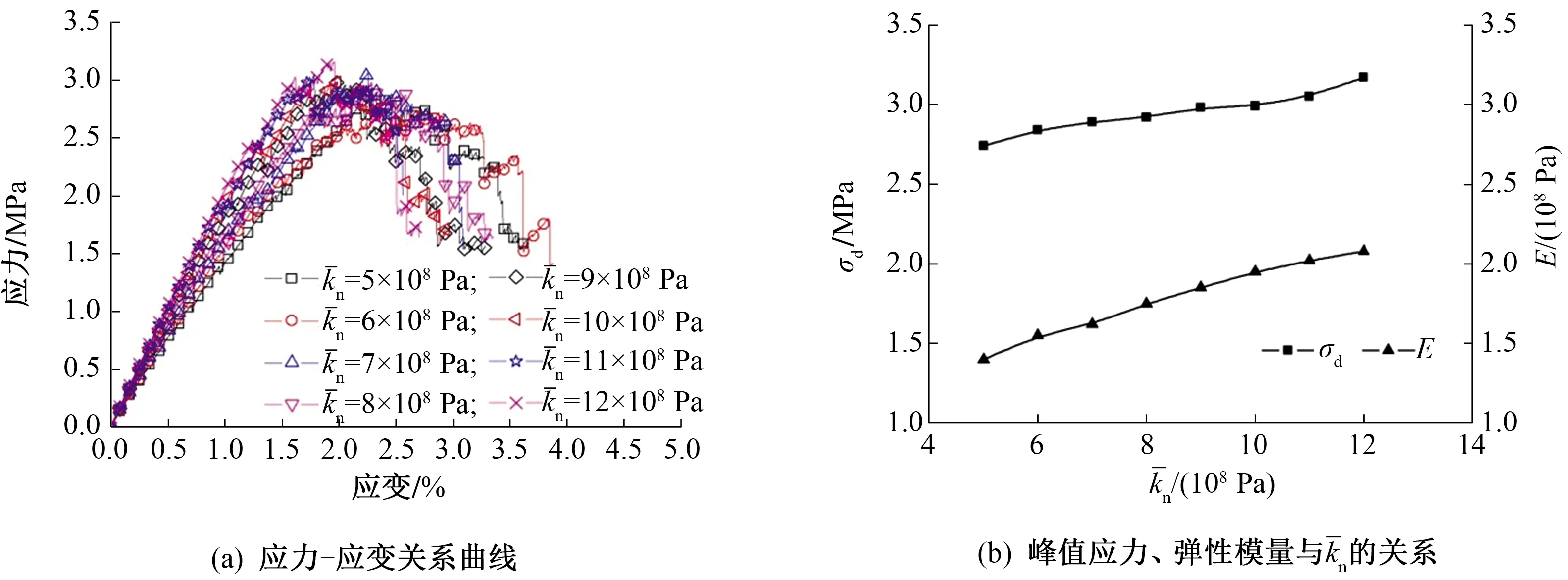
图3 不同时，试件的宏观参数响应关系

式中:σd的单位为MPa;E的单位为108Pa。

图4 不同时，试件的破坏形式

2.2 平行黏结切向刚度对宏观参数的影响

图5 不同时，试件的宏观参数响应关系

式中E的单位为108Pa。

图6 不同时，试件的破坏形式

2.3 接触黏结法向刚度kn对宏观参数的影响

不同kn下试件的应力-应变曲线,峰值应力σd和弹性模量E与kn的关系曲线如图7所示。由图7可知,随着kn的增大,试件达到峰值应力时对应的应变逐渐减小;峰值应力后的应力-应变曲线基本相似;σd表现出一定的离散性,整体上呈现减小的趋势,但变化范围很小,可以认为kn在一定范围内的变化对σd的影响较小;E随着kn的增大呈线性增加,其与kn的关系式为：

E=1.083+0.876kn(R2=0.983)。

式中E的单位为108Pa。

图7 不同kn时，试件的宏观参数响应关系

不同kn时试件的破坏形式如图8所示。由图8可知:kn=5×108Pa时,试件上贯通性共轭裂缝不对称,在对角线裂缝一侧有平行于试件的次生裂缝带;随着kn的增大,试件的贯通性共轭裂缝又表现为对称分布,破坏带逐渐加宽,破坏面交叉处次生裂纹增加,破坏交叉处的颗粒呈散粒体,以剪切破坏产生的裂纹为主。总体来看,kn对试件的破坏形式有一定影响。

图8 不同kn时，试件的破坏形式

2.4 接触黏结切向刚度ks对宏观参数的影响

不同ks时试件的应力-应变曲线,σd和E与ks的关系曲线如图9所示。

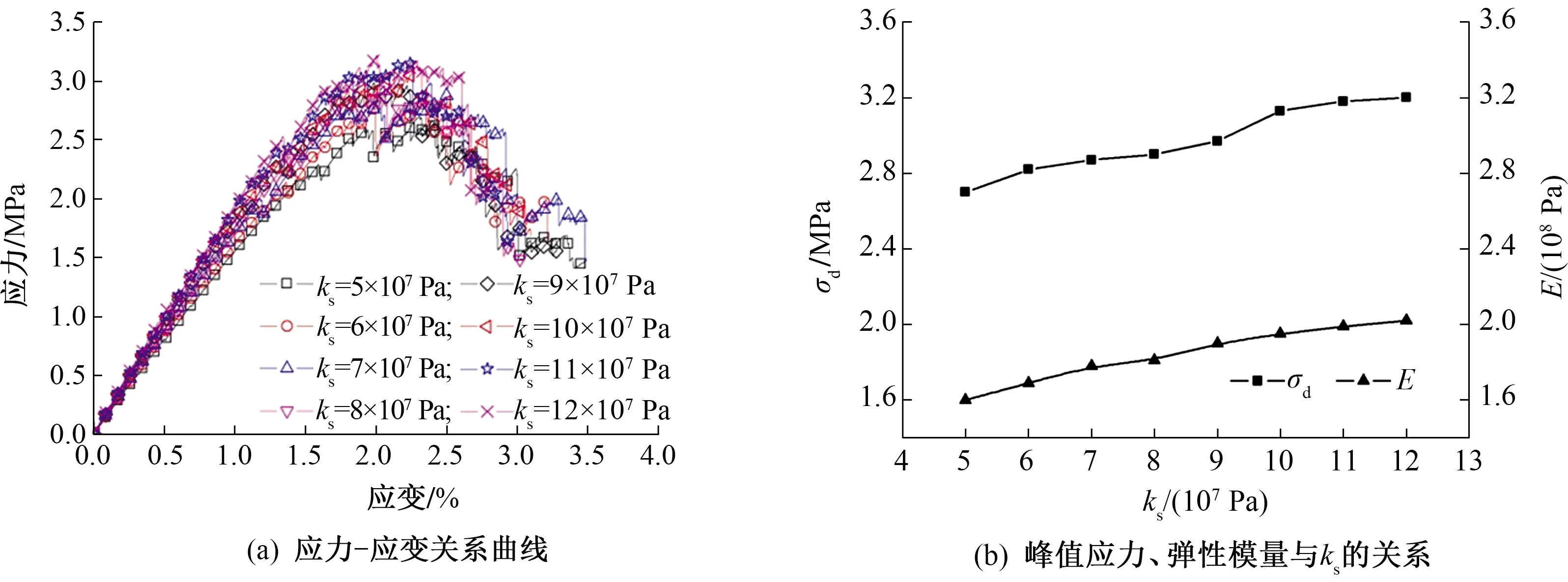
图9 不同ks时，试件的宏观参数响应关系

由图9可知:ks越大,试件应力-应变曲线上直线上升段的斜率越大,即弹性模量越大,应力峰值也越大,且其对应的应变值相应逐渐增大;应力-应变曲线上的下降段基本相似;σd随ks的增大而增大,其变化范围为2.7～3.22 MPa。E随ks的增大呈线性增长,其与ks关系式为：

E=1.332+0.6ks(R2=0.980)。

式中E的单位为108Pa。

不同ks时,试件的破坏形式如图10所示。由图10可以看出:当ks=5×107Pa时,贯通破坏面位于试件第一条对角线的方向;随着ks的增大,试件发生沿两对角线方向的共轭型破坏,沿对角线方向出现了平行破裂带,交叉破坏处有少量次生裂缝;当ks=12×107Pa时,主贯通破坏面又以第一条对角线方向为主,共轭型破坏不明显,第二条对角线方向的裂缝未贯通。总体来看,ks值对试件破坏模式的影响较大。

图10 不同ks时，试件的破坏形式

2.5 摩擦系数f对宏观参数的影响

对于CSG材料,试件出现裂纹后,骨料之间的摩擦对试件的力学响应存在较大的影响。不同f时，试件的应力-应变曲线、峰值应力σd和弹性模量E与f之间的关系曲线如图11所示。

由图11(a)可知:在应力达到峰值前,随着f的增大,试件应力-应变曲线的上升段逐渐变陡,峰值应力σd逐渐增大,但峰值应力σd对应的应变则较为接近;当f较小时,试件应力-应变曲线的下降段较平缓,随着f的增大,下降段逐渐变陡,表明f对材料的软化特性有很大的影响。

通过多组试验分析了摩擦系数f对试样宏观力学的敏感性,发现峰值应力σd和弹性模量E与f之间均表现为指数函数关系,如图11(b)所示,其关系式为:

式中:σd的单位为MPa;E的单位为108Pa。

不同f时,试件的破坏模式如图12所示。由图12可知:当f=0.3时,试件左侧局部剪胀明显,造成三角形脱落块体,形成非对称性破坏;当f=0.6、0.9、1.8时,试样均沿第一条对角线方向出现单一贯通破裂面,且f越大,第二条对角线方向上的裂缝越多,但破坏面不贯通;当f=2.4时,试件又表现为共轭型贯通破坏。总体来看,摩擦系数f对破坏面的影响较大,随着f的增大,试样由沿一个对角线方向产生贯通破坏向共轭型破坏转变。

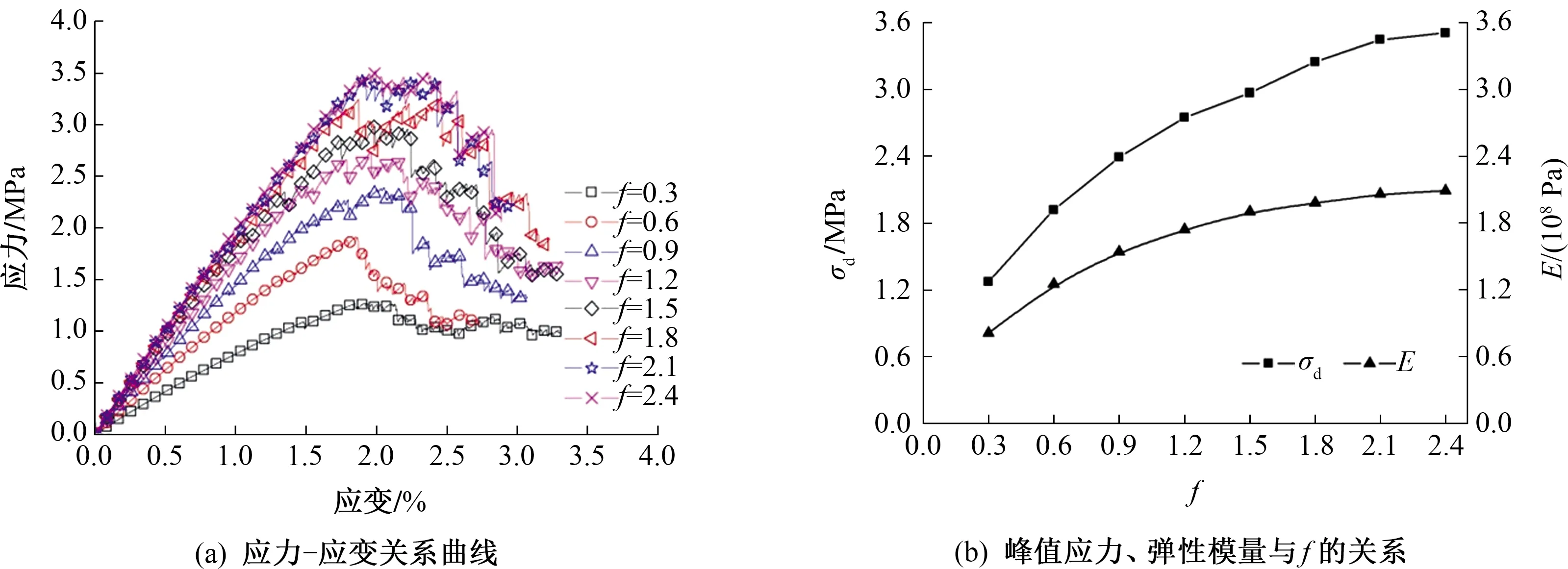
图11 不同f时，试件的宏观参数响应关系

2.6 平行黏结黏聚力对宏观参数的影响

式中σd的单位为MPa。

图13 不同时，试件的宏观参数响应关系

图14 不同时，试件的破坏形式

2.7 平行黏结抗拉强度对宏观参数的影响

图15 不同时,试件的宏观参数响应关系

图16 不同时,试件的破坏形式

3 宏、细观参数关系的建立

3.1 颗粒流细观参数确定

由于颗粒流模型中细观参数交叉影响的不确定性,根据以上建立的宏、细观参数间的量化关系,可为合理选取CSG材料的细观参数提供规律性的指导;再结合室内试验结果,采用正交设计的方法[15],寻找CSG材料细观参数的最优组合。具体步骤为:①以材料的弹性模量E、峰值应力σd、应力-应变曲线以及破坏形式作为正交设计试验的衡量指标;②选定7种细观参数作为基本因素,在一定的细观参数区间,将每种因素设定为8种取值水平,确定7因素8水平的因素水平表;③依据正交设计原理,以7种指标结合的形式来描述试验结果,通过评价各因素对试验指标的影响,进而确定合理的细观参数组合。最终确定试验的细观参数见表1。

表1 CSG材料的细观参数标定值

3.2 宏、细观力学特征验证

根据颗粒流数值模拟与室内试验的宏观力学特性,对试件的应力-应变曲线、强度参数和破坏形式进行对比分析。

3.2.1 应力-应变曲线

数值模拟试验和室内试验的试件应力-应变曲线如图17所示。室内试验所得的应力-应变曲线可分为4部分,即:初始压密段(OA)、直线上升段(AB)、屈服段(BC)和软化阶段 (CD)。OA段为试件内部空隙的闭合过程,呈非线性上升趋势;AB段时，材料表现为线弹性;B点以后,应力-应变曲线呈非线性增长,材料进入屈服阶段;当达到应力峰值即C点后,应力-应变曲线开始下降,即试件表现出软化特性[6,10,16]。

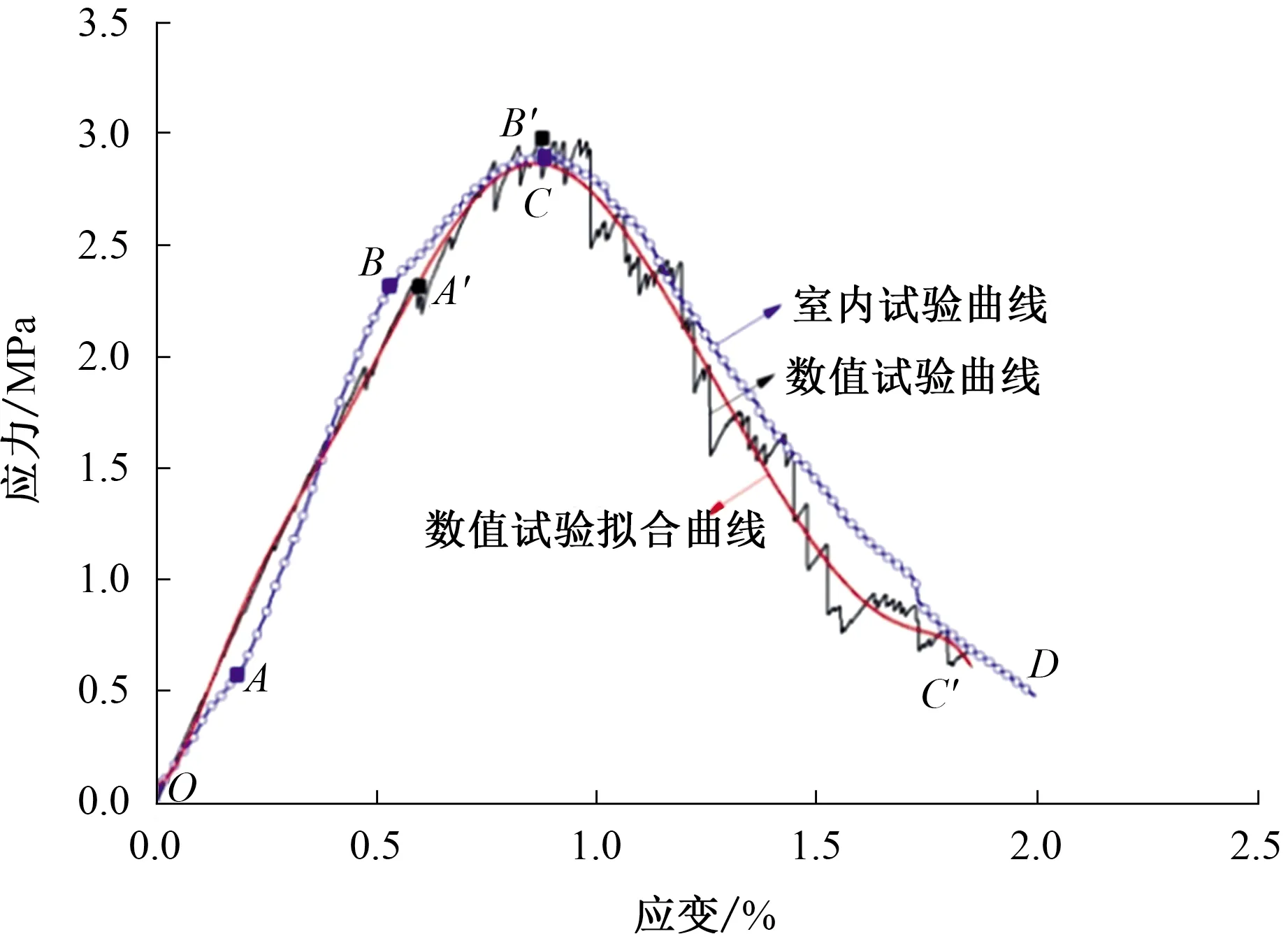
图17 室内试验与数值模拟试验中 试件的应力-应变关系

由数值模拟试验所得的应力-应变曲线,可分为3个阶段,即线性上升段(OA′)、非线性上升段(A′B′)和下降段(B′C′)。与室内试验结果相比,数值试验结果显示无压密阶段,这与数值模型的生成有密切关系:为了保证在重力作用下颗粒间能够均匀接触,在数值模型生成过程中进行了重生成压密,施加了内部压力,导致模型内部颗粒处于紧密状态。

若忽略应力-应变曲线的初始阶段,由图17可以看出,2种试验方式下所得的应力-应变曲线(特别是数值拟合曲线)具有很大的相似度,尤其是屈服点(B点)以后的曲线分布形式几乎相同。

3.2.2 强度参数

不考虑室内试验压密阶段的影响,材料的弹性模量可利用试件应力-应变曲线的直线段来计算。室内单轴压缩试验和数值试验得到的宏观参数见表2。与室内试验结果相比,数值试验中弹性模量E的相对误差为3.2%,峰值强度的相对误差为0.7%。总体来看,数值试验结果的误差还是比较小的,可认为确定的细观参数是可信的。

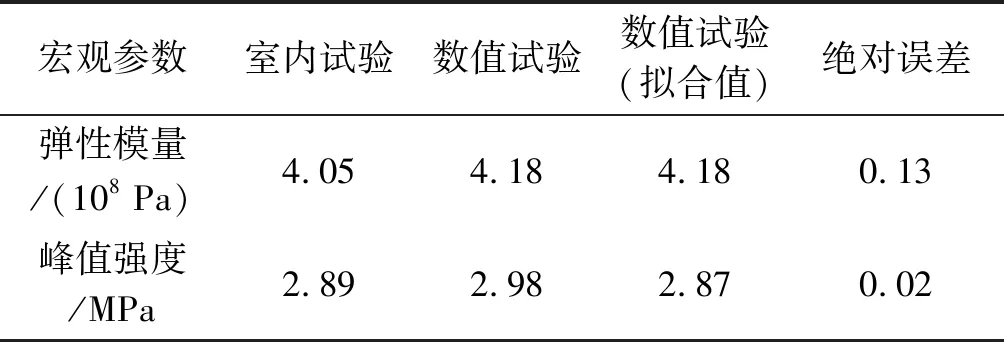
表2 室内试验与数值试验的结果对比

3.2.3 破坏形式

室内单轴压缩试验时,试件的破坏形式如图18所示。从室内试验试件的最终破坏形式看,试件呈共轭型破坏,将试件表面已开裂和脱离的部分清除后,试件上下两端呈锥形(图18(d));从整个破坏过程来看,试件表面的第一条可见裂缝出现在靠近顶部的外侧,裂缝短而细(图18(a));随着荷载的增加,试件开始向周围膨胀,表面竖向裂缝逐渐增多(图18(b)),随着竖向裂缝间的贯通,沿45°和135°方向的两条主裂缝出现,在剪胀作用的影响下,外侧开始脱落(图18(c)),试件整体出现剪胀破坏。

数值试验时,试件的破坏形式如图19所示。其最终破坏形式也为共轭型破坏,且两端呈锥型,两条破裂面的角度分别在45°和135°左右(图19(l)),与室内试验结果近似;破坏面主要由压剪破坏形成。从整个过程来看,试件的第一个裂纹出现在顶部的边缘处(图19(a));随着荷载的增加,内部的第一个裂纹出现在试件的中间(图19(c)),随后开始沿第一条对角线方向向上、下两端扩散,同时顶部和底部的裂纹沿第一条对角线和第二条对角线方向向试件中间扩散(图19(h));最后多个裂纹连通形成贯通裂缝,形成共轭型破坏,试件上下两端呈锥型。数值试验时,试件的裂缝主要位于试件内部,外部无裂缝出现。由于试件的破坏是从内部开始的,试件在受力过程中表现出剪胀特性。

对比分析上述两种不同试验结果可知,根据试件的剪胀性表现,从裂纹的萌生、扩展以及最终连通形成裂缝的破坏形式来看,用于数值试验模拟的细观参数取值是可靠的。

4 CSG材料细观破坏研究

室内试验研究仅能从宏观表象上解释CSG材料的宏观力学特性,要想真正揭示CSG材料的受力机理和破坏过程,通过宏观、细观多尺度相结合的方式是一种有效的手段,更有利于从本质上认识CSG材料的力学特性。本部分通过对CSG料的细观变形破坏机制进行数值模拟,阐述其细观破坏过程。

图19为CSG试件在单轴压缩条件下细观开裂过程中的典型截图及对应的应力-时间步关系。

图19 试件破坏演变过程

图19中：在应力达到峰值之前,当时间步t=3 886 760时,试样顶部A区出现第一个裂纹,位于颗粒一侧。随着加载的进行,当t=4 722 760时,第一个裂纹处的颗粒四周均出现不同的裂纹,该颗粒与周围颗粒间的黏结键全部断裂,与相邻颗粒失去了黏结作用,应力曲线上出现了小幅应力降。第二个裂纹区B位于试件中间,此时t=5 809 760,A区的裂纹沿第一条对角线方向向下扩展。当t=6 088 760时,B区的裂纹沿第一条对角线方向向上扩展,A区的裂纹继续向下扩展,A区和B区的裂纹相向发展,裂纹呈间断性分布,此时试件顶部左侧C区和中部右下角D区均出现第一个裂纹。当t=6 537 760时,A区和B区的裂纹继续增多并相向发展,裂纹呈间断性分布。当t=6 926 760时,试样底部左下角E区出现多个裂纹并形成第一条裂缝,裂缝细而短,此时试件应力达到峰值。当t=7 614 760时,C区和D区的裂纹向中部B区扩散,裂纹分布为间断性,试件底部右下角F区出现多个裂纹。峰值过后,当t=7 859 760时,B区与A区、D区的裂纹连通形成裂缝,且B区裂缝沿第一条对角线方向向下发展,形成沿第一条对角线方向的主裂缝,但该主裂缝并未贯通整个试件,试件仍具有一定的承载能力,同时出现大幅度应力降。当t=8 455 760时,第一条对角线方向主裂缝两侧出现次生裂缝,长度不大或呈离散形分布,同时出现应力降。此后的一段时间内,试件内部裂缝的发展以B区周边的次生裂纹为主,主要集中在靠近C区和E区的区域。当t=9 547 760时,沿第一条对角线的主裂缝基本贯通,主裂缝表层粗糙,且裂缝宽度不均,上部和下部较宽,中间偏窄。当t=11 793 760时,沿第一条对角线方向的主裂缝完全贯通,裂缝宽度增大,同时沿第二条对角线方向裂缝基本形成,试件应力快速减小,出现较大的应力降。当t=13 443 760时,由于第一条对角线方向主裂缝表面粗糙,靠着颗粒间的摩擦,试件仍具有一定的抗压能力,但随着试件的膨胀变形增大,试件开始向两侧快速膨胀,从而导致第二条对角线方向的裂缝逐渐增加,但裂缝宽度较小(为张拉裂缝),并由B区向C区和F区扩展。当B区与C区和F区的分散裂缝连通后,试件呈共轭型破坏,试件两侧的块体脱落,试件呈双锥型。从试件破坏的模拟过程看,试件的破坏主要是由于颗粒间黏结键的破坏引起的。同时,室内试验也说明了这一点,试件破坏时骨料并未破坏,而是胶凝材料和骨料间发生分离造成了试件破坏[6,17]。由此可见,试件的强度决定于胶凝材料的多少和包裹度。

整个加载过程中，试件的应力及裂纹数量分布如图20所示。由图20可知,应力-时间步曲线的应力峰前阶段可分为直线上升段和非线性上升段两部分。a点之前,试件内无裂纹出现。a点时,试件内出现第一个裂纹。b点时,少量颗粒周边裂纹完全开展,此后应力曲线呈非线性上升趋势。a点和b点均出现较小的应力降,但并未影响试件的整体受力。随着应力的增加,在点c、d、e时刻,应力变化不大,但裂纹数量增幅较大,导致峰前损伤突出。当应力接近峰值应力(f点)时,曲线上的应力降出现频繁,裂纹逐渐增多,且分布离散。应力峰值后的h点,出现大幅度应力降,裂纹数在短时间内快速增加,并开始贯通成大裂缝,主破裂带雏型出现。从裂纹数量的分布来看,在达到应力峰值之前,试件内部裂纹数量较少;在应力峰值附近,裂纹数量基本呈等速增长(d点至g点);应力峰值以后,随着每一次应力降的出现,裂纹数量出现大幅突增(h、i、j点),裂纹增长速率增大;在应力峰值后的h点至k点之间,产生裂纹的数量占整个试验过程裂纹总量的75%左右。大量裂纹产生并贯通是试件出现整体破坏的前提,同时,裂纹的逐渐增多使试件内部的有效受力面积减小,试件表现出软化特性。

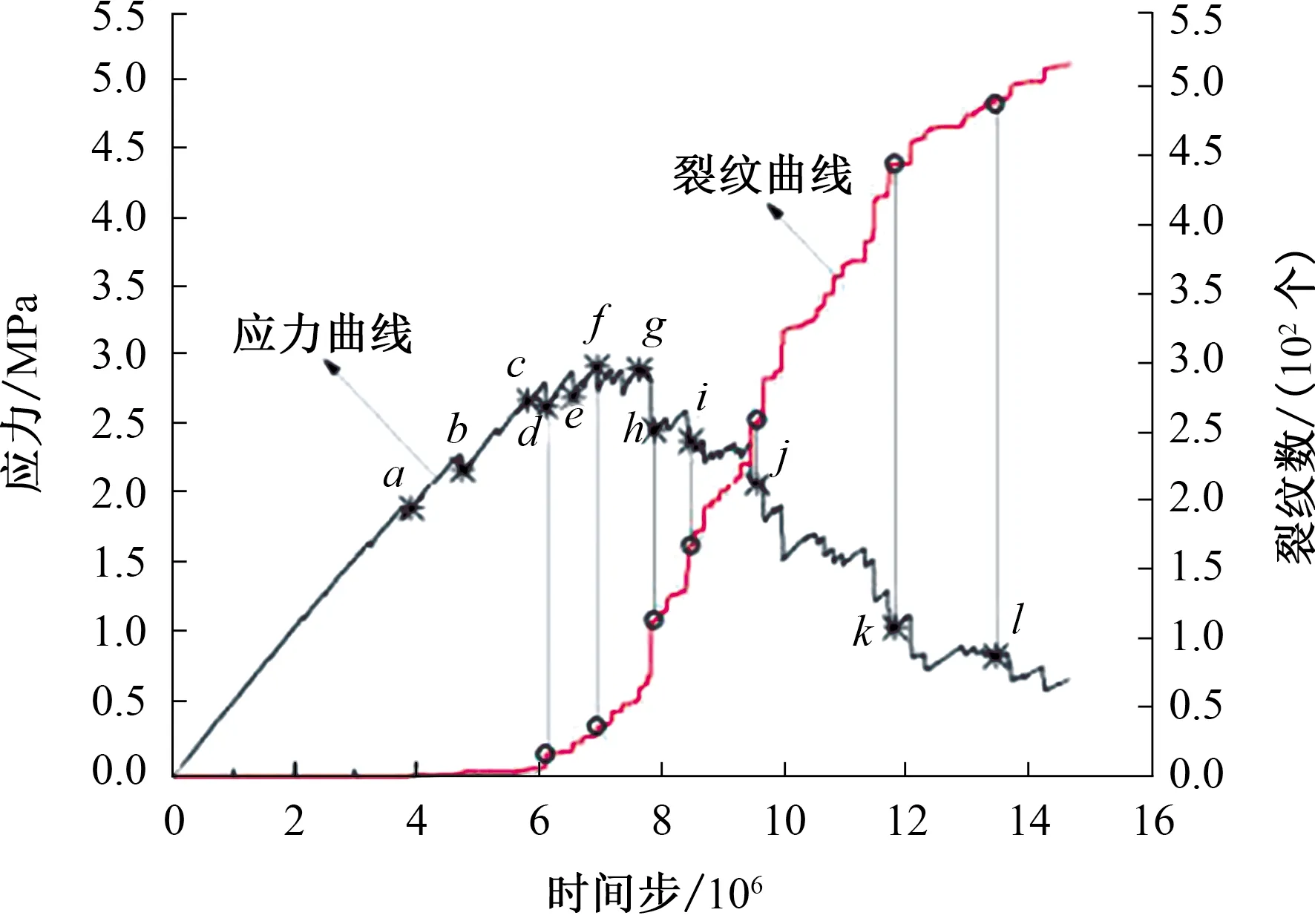
图20 应力及裂纹数量分布关系

5 结论

本文采用室内试验和数值模拟两种方式,建立特定配合比下CSG材料的宏观力学指标与细观参数之间的定量关系,确定了反映CSG材料宏观力学特性的细观参数,并对CSG材料的破坏机理进行了研究,得出以下结论。

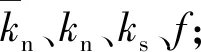
2)在压缩过程中,当应力达到试件的弹性极限强度后,伴随着应力降,试件内部出现局部连通的小裂缝;此后应力降出现频繁,裂纹逐渐增多,在应力峰值之前,试件中部出现裂纹,呈离散型分布,并成为裂纹的主分布区;在应力峰值以后,伴随着较大应力降出现的瞬间,第一条主裂缝方向的小裂缝连通形成贯通面,随后,在压剪作用下,伴随着第二条主裂缝的产生,试件表现出明显的剪胀特征。

3)分析室内试验和数值模拟试验,试件最终发生共轭型破坏。室内试验从宏观表象上反映了试件的破坏过程,颗粒流模拟方法从细观的角度反映了材料的内在受力机理和破坏过程,更能从本质上揭示材料的损伤发展过程和力学特性,对深入认识CSG材料具有重要意义。