岩石结构的定量评价及其与岩石力学性质的关系

2020-09-03谢山立代晨飞袁广祥

华北水利水电大学学报(自然科学版) 2020年4期

谢山立，代晨飞，袁广祥

(1.河南省地矿建设工程(集团)有限公司,河南郑州 450007; 2.华北水利水电大学地球科学与工程学院,河南郑州 450046)

岩石结构是指组成岩石的矿物的结晶程度、颗粒大小、形态及它们之间的相互关系[1]。一般包括：矿物颗粒的大小、形状、方位，斑晶与基质的比例，晶粒的相对比例，基质材料与类型，胶结方式、胶结程度，孔隙率，颗粒边界条件或颗粒间的接触关系[2]。由于岩石的地质本质性[3]，岩石结构对岩石的力学性质具有明显的影响[4-6]。一些学者对二者的关系进行了研究:JOHANSSON E发现矿物颗粒大小、云母含量及微裂隙的发生频率对花岗岩和辉长岩的力学性质影响显著[6]；赵斌等定性分析了9种岩石的力学性质，认为矿物成分和细观结构对其有显著的影响[7]；张勇等认为葛洲坝砂岩的矿物成分、颗粒粒度、胶结物成分、胶结类型等对其力学性质起决定作用，且发现中粗、中细砂岩强度高于细砂岩的强度[8]；刘晓丽等认为砂岩的弹性模量和单轴抗压强度随孔隙度的增大而减小[9]；孟召平等对煤层顶底板沉积岩进行了研究，发现随着粒径大于0.03 mm(或小于5φ)的碎屑颗粒含量的增加，碎屑岩的力学性质发生跃变[10]；卫宏等发现大同燕子山煤层顶板岩石的显微空隙和粒度的分形维数与岩石强度具有明显的相关性[11]；朱长歧等发现南海不同岛礁及沿岸海滩岩的单轴抗压强度随着密度及胶结程度的增加而明显升高[12]；HECHT C A 等认为石炭—二叠纪红层的强度和变形性质取决于岩石结构和矿物组成[13]；VALDIVIEZO-MIJANGOS O C等发现页岩的矿物组成(石英、碳酸盐岩和黏土)对其动力特征具有显著的影响[14]；LIU Z B等认为泥岩结构的各向异性对其蠕变具有明显的影响[15]；ÖMER ÜNDÜL等发现安山岩的矿物成分及其含量对裂缝萌生阈值和单轴抗压强度具有显著的影响[16]；POLA A等认为火山岩的孔隙结构、岩石结构、基质胶结、晶体和碎屑排列等明显影响其力学性质和破坏特征[17-18]；于庆磊等通过数值模拟发现岩石强度对其内部结构的细节非常敏感[19]；李晓鄂和蔡胜华研究了三峡坝址区闪云斜长花岗岩，认为其强度是由组成岩石的矿物成分和这些矿物颗粒的彼此镶嵌组合的紧密程度决定的[20]；TUGRUL A等对土耳其一些地方花岗岩的粒径、石英含量进行了研究，发现其对花岗岩力学性质的影响显著[21]；PRIKRYL R对捷克波希米亚高地花岗岩的单轴抗压强度与矿物颗粒大小进行了研究，发现二者具有对数关系[22]；KEIKHA T等研究了伊朗东部2种类型花岗岩，发现力学性质与其结构特征(矿物颗粒大小、矿物成分以及高强度矿物与软弱矿物的比值)具有明显的相关性[23]；MAKANI A等建立了法国上加龙省花岗岩矿物组成与其物理力学性质之间的关系[24]；GUPTA V等发现石英岩的无侧限抗压强度与岩石结构具有明显的相关性[25]；ALBER M等建立了断层角砾岩的结构与单轴抗压强度之间的关系[26]；袁广祥等通过研究阿拉善巴彦诺日公花岗岩，发现对其力学性质影响最大的是钾长石和黑云母[27]，微裂隙对花岗岩的单轴抗压强度和变形模量有明显的影响[28]；韩振华等发现阿拉善巴彦诺日公花岗岩的矿物粒径对岩石力学特性的影响明显[29]。

综上可以看出，目前对岩石结构与力学性质之间关系的研究主要以定性分析为主，部分进行了半定量化研究。由于岩石的复杂性，本文拟根据HOWARTH D F等提出的结构系数(Textural Coefficient)[30-31]，并结合已有的研究数据，分析岩石结构与岩石力学性质之间的定量关系。

1 岩石结构系数的概念

为了对岩石结构进行定量评价，HOWARTH D F等从矿物颗粒的形状、矿物颗粒延性(计算其圆度与长宽比)、矿物颗粒方位、颗粒总面积占总计算面积(包括基质面积)的比例等4个方面提出了“结构系数”(Texture Coefficient)的概念[31]，并给出了具体的计算公式：

(1)

式中：TC为结构系数；AW为颗粒面积加权(颗粒累计密度)；N0为长宽比小于预设判别值的颗粒数量；N1为长宽比大于预设判别值的颗粒数量；FF0为长宽比小于预设判别值颗粒形状系数的算术平均值；AR1为长宽比大于预设判别值的颗粒长宽比的算术平均值；AF1为长宽比大于预设判别值的颗粒的方位系数。

根据地质矿产行业标准《岩矿鉴定技术规范第4部分：岩石薄片鉴定》(DZ/T 0275.4—2015)[32]和石油天然气行业标准《岩石薄片鉴定》(SY/T 5368—2000)[33]，对岩石样品进行薄片鉴定，获得岩石的结构特征，并利用图片处理技术[34-36]获取公式(1)中所需要的参数。

颗粒面积加权(颗粒累计密度)是指颗粒总面积占总计算面积(包括基质面积)的比例。在计算颗粒面积加权时，只测量观察窗口中的完整颗粒，如图1所示[2]，与观察边界接触的不完整颗粒不统计。总面积也不是观察窗口的面积，而是仅包括完整颗粒的区域面积(图1中计算边界包含的面积)。

图1 砂岩的薄片颗粒轮廓(根据照片简化)

岩石中的矿物颗粒形状一般是不规则的，很难准确表示其长、宽、高等参数。在岩石薄片中矿物颗粒表现为不规则的多边形，其长度和宽度一般取费雷特直径的最大值和最小值。费雷特直径是颗粒边界上两条相互平行的外切线的距离。图2给出了利用费雷特直径确定矿物颗粒长度和宽度的方法[31]，以此种方法确定的矿物颗粒的长轴方向与短轴方向不一定垂直。长宽比的预设判别值一般取2。

图2 费雷特直径的最大值和最小值(长度和宽度)示意图

形状系数(FF)用颗粒的圆度表示。其计算方法是薄片上颗粒的面积与具有相同周长的圆面积的比值，如公式(2)所示：

(2)

式中：A为薄片中颗粒面积；P为薄片中颗粒周长。

矿物颗粒的方位利用颗粒的长度方向与水平方向的夹角表示，最大值为180°。由此可见，矿物颗粒方位的影响只有在长宽比较大的情况下才比较明显，因此，在统计方位系数时只统计长宽比大于2的颗粒。方位系数主要体现为颗粒之间的夹角(利用颗粒长度方向的夹角表示)。进行颗粒统计时，为计算AF1，只考虑夹角中的锐角。对于N个颗粒，其角度差异的数量为：

(3)

对不同的夹角，赋予不同的权重，具体见表1[31]。

表1 颗粒间夹角(锐角)的分级及权重

利用公式(4)计算颗粒的方位系数：

(4)

式中：N为长宽比大于2的颗粒总数；Xi为每组夹角的数量；i为组数及权重。

2 岩石结构系数与力学性质的定量化关系

由于岩石结构系数能够定量描述岩石结构，并能和岩石的力学性质(主要是强度)建立量化关系。因此，多位学者开展了这方面的研究。此外，由于岩石结构包含的因素不止结构系数中所体现的因素，不同的岩石对应的量化关系式明显不同。

通过对24个断层角砾岩的样品进行分析，发现其结构系数(TC)与其单轴抗压强度(UCS)具有明显的对数关系[26]，结果如图3所示。

从图3中可以看出，结构系数在0.3和0.6之间的数据比较集中，其与单轴抗压强度呈明显的线性关系，如图4所示[26]。

图3 断层角砾岩结构系数与其单轴抗压强度的关系

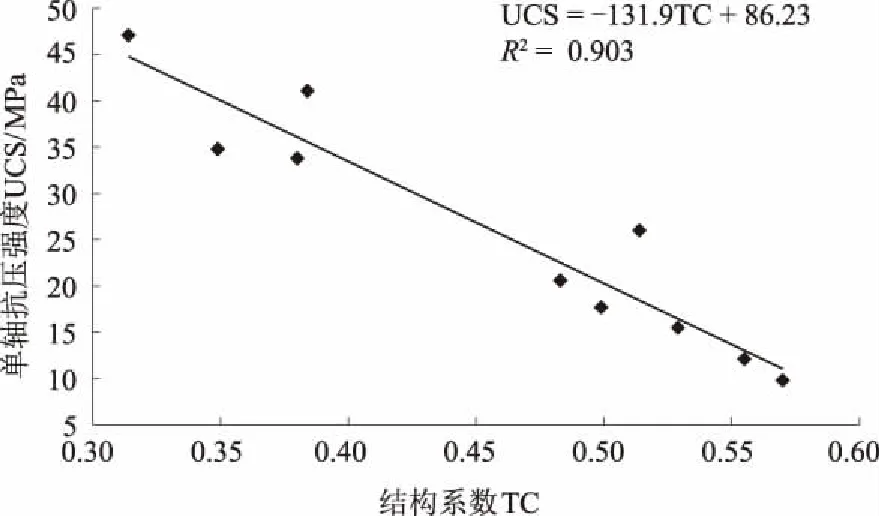
图4 断层角砾岩结构系数(0.30～0.60)与其单轴抗压强度之间的关系

分析喜马拉雅西北地区的18个石英岩样品，发现石英岩的结构系数与其单轴抗压强度具有一定的线性关系[25]，如图5所示。

图5 石英岩结构系数与其单轴抗压强度之间的关系

综合分析砂岩、大理岩、玄武岩、花岗岩、角岩、微正长岩等6种岩石的结构系数与其力学性质的关系，发现岩石的力学性质与结构系数具有明显的二次函数关系，如图6所示[31]。但是，对于不同的力学性质，其关系式不同。从图6(b)和图6(c)中可以看出，干燥状态和饱和状态下的单轴抗拉强度的关系曲线也有一定的区别。

图6 一些岩石结构系数与其力学性质之间的关系

3 讨论及结果

岩石的结构系数是岩石中颗粒的形状、大小、方位及含量的综合反映。因此，结构系数与力学性质具有明显的相关性，可以用公式表达两者的关系，从图3—6中即可看出，但这种关系并不具有普适性。在图3中，断层角砾岩的结构系数与其单轴抗压强度呈明显的对数关系；在图5中，石英岩的结构系数与其单轴抗压强度则呈线性相关；图6中同时对比多种岩石，却呈现为明显的抛物线关系。对比图3和图4，即使是同一种岩石，其结构系数不同，与单轴抗压强度的相关性也有明显的差异。图3中针对所有样品，二者呈对数相关；图4中针对结构系数在0.30～0.60范围内的样品，二者呈显著的线性相关。

岩石的力学性质不仅受结构系数所体现的颗粒的形状、大小、方位及含量的影响，同时还受到岩石中颗粒的力学性质、颗粒之间的胶结方式和胶结程度等因素的影响，而这些因素并未体现在岩石的结构系数中。因此，尽管岩石的结构系数与其力学性质具有相关性，图3—6也给出了一些岩石的结构系数与其力学性质之间的关系式，但多数岩石的结构系数与其力学性质之间很难建立起很好的数学关系式。不同的岩石，由于其颗粒成分、胶结方式等方面的差异，建立严格的数学关系式更难。例如：图3和图4所示的断层角砾岩结构系数与其单轴抗压强度呈负相关关系；而图5和图6中岩石结构系数与其单轴抗压强度呈正相关关系。也有研究表明，岩石的结构系数与其力学性质的相关性较差，但与孔隙率、密度等物理性质具有很好的相关性，如OZTURK C A等对某一钻孔不同深度的岩石(包括石灰岩、安山岩、凝灰岩及微晶质的岩石)的研究成果，如图7所示[37]。