面向计算思维能力培养的STEM+C教育案例探究——以“基于SIR模型的疾病传播模拟”活动为例

曹晓靓

（中国福利会少年宫）

一、STEM教育和少儿编程教育教学实施现状

（一）发现问题

1. 本土化的优质STEM教育课程缺乏

2017年发布的《中国STEAM教育发展报告》指出，目前国内的STEM课程还存在着诸多“水土不服”：STEM教学体系和评价缺乏系统化规范；相关教学资源的配置与使用在设计并实施一个STEM课程中至关重要，硬件设施和材料在开展课程时的损耗较高，这导致了STEM课程经费负担重、课程更新慢；目前还呈现出学科整合不到位、相关经验迁移难、资源共享难、师资严重缺乏等问题。通过文献研究和教学实践总结，发现能够真正做到“跨学科”和“真落实”的本土化优质STEM课程并不多[1]。

2.少儿编程教育多注重技术忽视探究

近年来，随着人工智能的发展，少儿编程教育的浪潮席卷全球。2017年中国国务院印发的《新一代人工智能发展规划》中也明确提出应逐步在中小学推广编程教育[2]。由此可见，青少年编程教育的普及是目前迫切需要的。虽然近年来计算思维的培养开始依托编程教育逐渐蓬勃发展起来，但通过研究者们的调查发现，大多发生在校内信息技术课堂上的编程教育内容都侧重编程语法和算法构建，却往往忽视了在探究学习中培养学生创新素养和跨学科解决真实问题的能力。

（二）SWOT分析法

20世纪80年代初，由美国旧金山大学的管理学教授韦里克提出的SWOT分析法常被用于竞争对手分析和企业战略制定等场合，它是基于矩阵图思维框架的一种分析方法。主要截取组织发展的四个维度：优势（S）、劣势（W）、机会（O）、威胁（T），然后通过归纳、对比和概括对组织状况进行系统分析[3]。笔者主要采取文献研究法，运用SWOT分析的原理，从四个维度对国内STEM教育一线教学实施现状进行了分析和总结，使得培养计算思维的STEM+C（Computing）课程开发设计更具科学化。

（三）基于国内STEM教育一线教学实施现状的SWOT矩阵

由于图形化编程语言成本低、易于线上推广、远程培训教师，以图形化编程语言为辅助技术支持的STEM+C（Computing）课程能够大大降低STEM教育的学习门槛；同时可以做到上下延伸，良好衔接，上接图形化语言、STEAM多元化资源，下接开源开发板、物联网硬件；融入机器学习、图像识别等人工智能技术后也提升并开阔了STEM课程内容的高度与宽度，在学生思维的过渡期，可以起到很好的衔接作用。另一方面STEM的融合也有助于弥补现有编程课程体系中跨学科解决真实问题的能力和创新素质培养上的不足。

表1 基于国内STEM教育一线教学实施现状的SWOT分析表

计算思维强调要基于真实问题展开，充分利用计算机科学的概念和方法解决真实情境中存在的问题。与之相似的一点，STEM教育同样是注重通过多学科知识和多元化工具去解决真实情境中的复杂问题。因此，开发面向计算思维能力培养的STEM+C(computing计算)课程是极具现实意义和研究价值的。

二、基于STEM+C活动的计算思维培养模型设计

有国外学者提出，计算思维的包含“分解（Decomposition）、抽象（Abstraction）、算法 （Algorithms）、调试（Debugging）、迭代（Iteration） 和归纳（Generalization）”六个要素[4]。STEM课程注重探究、学科整合与真实情境的交互。在设计相关课程时，应培养学生独自探究与合作探究的能力。探究过程要注重课程之间的衔接性，调动学生的兴趣和求知欲，促使学习者自主发现并学会解决问题。设置层次分明的递进式任务，步步深入发展学生的高级思维，同时做好相关拓展课程的延伸和知识迁移。在设计课程时，应注重多学科间的深入整合，情境的创设与支持也应从双向考量，从真实情境中的问题出发再回归到真实情境中去。根据这些特点，笔者构建了如图1所示的基于STEM+C活动的计算思维培养模型。

图1 基于STEM+C活动的计算思维培养模型

三、教学案例剖析

下面通过对“基于SIR模型的疾病传播模拟”活动案例的分析，具体阐述上述模型的应用。活动中将利用计算思维的方式重新解构科学课的一些具体问题，以此掌握计算思维解决真实问题的方法和能力。

第一步：情境设置，激发兴趣

2020年新冠肺炎爆发，中国工程院院士钟南山早前曾预测南方地区2月中旬将会达到发病最高峰。那么，科学家是如何预测的呢？

第二步：定义问题，明确任务，知识储备

钟南山院士对疫情的预测并不是凭借经验，而是通过数学模型分析并结合实际情况作出的判断。下边我们就阐述如何一步步认识疾病传播的过程，从简单到复杂，建立起疾病传播模型，最后用图形化编程语言来实现疾病传播的模拟。

知识储备1—— 基本传染数

通常记做R0，它是指在没有外力介入，同时所有人都没有免疫力的情况下，一个感染者会把疾病传染给多少人的平均数[5]。R0的数目愈大，代表流行病的控制愈难，取决于当时各种环境因素，比如是否密闭空间、病患的症状和携带病毒的指数等。

知识储备2 —— SIR模型

经典的“易感者-感染者-免疫者”传染病模型，又叫SIR模型，像水痘、天花等疾病都遵循SIR模型，是指得了一次病就不会再得第二次。但有些疾病感染上之后可能下次还会患，就像我们最常见的感冒和流感，不会获得免疫力，它称之为“易感者-传染者-易感者”模型（SIS模型）。

第三步：问题分解-模式识别-抽象化

1.问题分解——化繁为简，各个击破

计算思维的第一个步骤是把复杂的问题分解成若干易于处理的小问题。我们可以将疾控中的人群分成三大类：易感者（S）、感染者（I）、免疫者（R）。

2.模式识别——分析辨认，厘清关系

构建出它们的关系模型：易感者→感染者→免疫者。

3.抽象化——联系旧识，模式归纳

定义“邻居”：把每个人抽象成一个方块，每个与方块任意一边相邻的方块“邻居”代表的是社交圈里的一个人，假设每个人有4个邻居。

定义“一格”：现实生活中从传染、生病到治愈都需要一定的时间，我们假设将这段时间周期称之为“1格”。

图2 抽象化

第四步：算法构建-流程设计-原型制造

1.算法开发——设定规则，制造解决

所谓算法，就是指模型运行的规则。

规则1：感染者有一定概率在下一步让易感者邻居成为感染者。

规则2：疾病只能通过感染者传播给“邻居”，而不能隔空传播。

图3 算法规则

2.流程设计

学生可以通过思维导图的方式进行数据流分析，梳理每个角色之间的结构关系和事件关系。

图4 “传染源”角色的流程图

图5 “易感者”角色的流程图

3.编写程序

随着一号病源的活动，陆陆续续有接触者被感染，从绿色变为黄色，然后发病转为红色，在有床位的情况下感染者被送往医院隔离治疗，但随着病毒大面积爆发，右上角的死亡病例数值逐渐攀升，到了后期治疗成功的蓝色康复者越来越多。这个治愈概率该如何表示呢？可以用随机数来解决这个问题！如果假设治愈率为70%，在1到100的数值范围内随机返回一个数值，而随机返回值大于30的概率有70%。

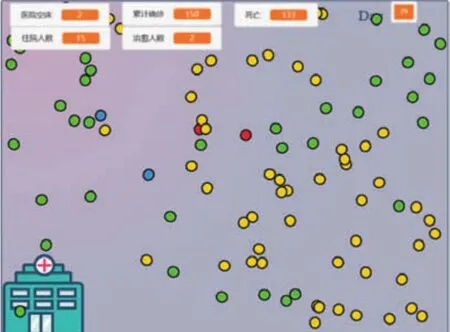
图6 场景设置

第五步：测试优化

接下来我们可以通过修改模拟规则增加挑战，让它更接近真实生活。

1.现实生活中，几乎不存在传染率为100%的疾病，大多数疾病是易感者接触了感染者后，有一定概率中招成为感染者，这就是我们前面说的传染率。可以将感染率设置为一个变量，在模型中通过拖动滑杆改变感染的概率。

2.如果是SIS模型下，又要改变哪些规则呢？

第六步：分享交流

1.请用自己的话描述一下基本传染数的概念。

2.除此之外，我们还可以用模拟验证一下戴口罩的意义，自己试试看吧！

四、总结与反思

这种运用计算机科学的基础概念去求解问题、设计系统和理解人类行为的思维模式就是计算思维[6]。此次是笔者STEM+C教育的案例探究，乐于与大家共享和探讨不足之处。STEM教育融入C（Computing）课程，是以信息化技术为抓手、基于项目式学习的方式，运用科学原理、数学计算、工程设计培养学生计算思维的有效手段。计算思维并不一定要通过编程来实现，它不是计算机的思维，而强调的是人的思想，所以它不能直接与编程思维画等号。计算思维的思想是要教会学生如何组织、分析，并且高效地解决生活或学习中的真实问题。所以建议教师力图将课堂与社会热点连接，提供解决真实情境中有效问题的机会，引导学生学会思考和分析己有方案的优缺点，简化、优化算法，逐步找到最优解决方案。学习再多的理论，都需要经过实践和不断反思，希望在过程中找到自己的不足，探索更好的教学方法，设计更利于学生计算思维发展的活动内容。