D-Z矩阵和D-Z B-矩阵线性互补问题解的误差界估计式的改进

周 平, 黄卫华

(文山学院数学与工程学院， 云南 文山 663099)

引 言

李艳艳等在文献[16]中给出如下结果：

以上两个估计式计算量大，当矩阵阶数很大时，计算困难，从而寻找简单易行的估计式是非常有必要的。关于D-ZB-矩阵的线性互补问题解的误差界估计问题，通过查阅相关文献目前没有相应的研究结果。

本文在前人研究的工作基础上进一步研究了该问题，得到了仅依赖于D-Z矩阵和D-ZB-矩阵元素的新估计式，且给出了D-ZB-矩阵最小奇异值的新结果，应用例子验证了这些新获得的估计式的有效性和优越性，提高了估计的精度。

1 预备知识

为了便于后文的研究，先给出如下记号：

N={1,2,…,n}，Cn×n(Rn×n)是全体n×n阶复(实)矩阵构成的集合。

设A=(aij)∈Cn×n，M=(mij)∈Cn×n，记

定义1[1]设A=(aij)∈Rn×n，q∈Rn，寻找解x∈Rn，使得

(Ax+q)Tx=0，Ax+q≥0，x≥0

则该问题称为线性互补问题，记作LCP(A,q)。

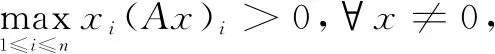
定义3[4]设A=(aij)∈Cn×n，如果∀i∈N,存在j∈N={1,2,…,n}，j≠i,使得

那么A叫做Dashnic-Zusmanovich矩阵，常记作D-Z矩阵。

定义4[4]设M=(mij)∈Rn×n，将M表示成M=B++C的形式，其中

(1)

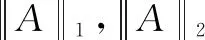
引理1[8]设A=(aij)∈Cn×n，它是P-矩阵，则LCP(A,q)的解存在且唯一。

引理2[8]设M是P-矩阵，x*和x分别是LCP(M,q)的精确解和近似解，则

其中：r(x)=min{x,Mx+q}，表示取向量x和Mx+q对应分量的最小值；x*表示LCP(M,q)的解；D=diag(d1,d2,…,dn),0≤di≤1。

引理3[8]设M是D-Z矩阵，则M是P-矩阵。

引理4[9]若γ>0,η≥0，则对任意的x∈[0,1]，有

且

引理5[7]设A=(aij)∈Cn×n为D-Z矩阵，则

引理6[7]设M=(mij)∈Cn×n为D-Z矩阵，且mii>0，如果B=I-D+DM，其中I是n阶单位矩阵,D=diag(di),0≤di≤1,i=1,2,…,n，那么B是D-Z矩阵。

2 主要结果

下面应用前文给出的相关定义和引理，并结合几个不等式的放缩技术，对D-Z矩阵和D-ZB-矩阵线性互补问题解的误差界进行研究，并结合引理5给出了D-ZB-矩阵的最小奇异值新下界。

其中：

ψi,j(M)=

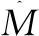
(2)

(3)

(4)

(5)

(6)

应用式(2)～式(6)，得

ψi,j(M)

即

故有

定理2设M=(mij)∈Cn×n是D-ZB-矩阵，将M表示成M=B++C的形式，其中B+与式(1)定义相同，则有

其中：

ψi,j(B+)=

证明设MD=I-D+DM，则

MD=I-D+D(B++C)=

(I-D+DB+)+DC

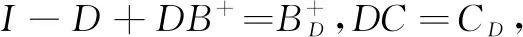
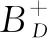
推论1设A=(aij)∈Rn×n是D-ZB-矩阵,则

推论2设A=(aij)∈Rn×n是D-ZB-矩阵,则A的最小奇异值

定理3设A=(aij)∈Rn×n是D-ZB-矩阵,则

σ1(A)≥σ2(A)

其中

β(A)=

证明因为文献[7]的定理3验证了

则

σ1(A)-σ2(A)=

所以

σ1(A)≥σ2(A)

下面用数值例子对文中给出的新估计式的有效性和可行性做进一步说明。

3 数值算例

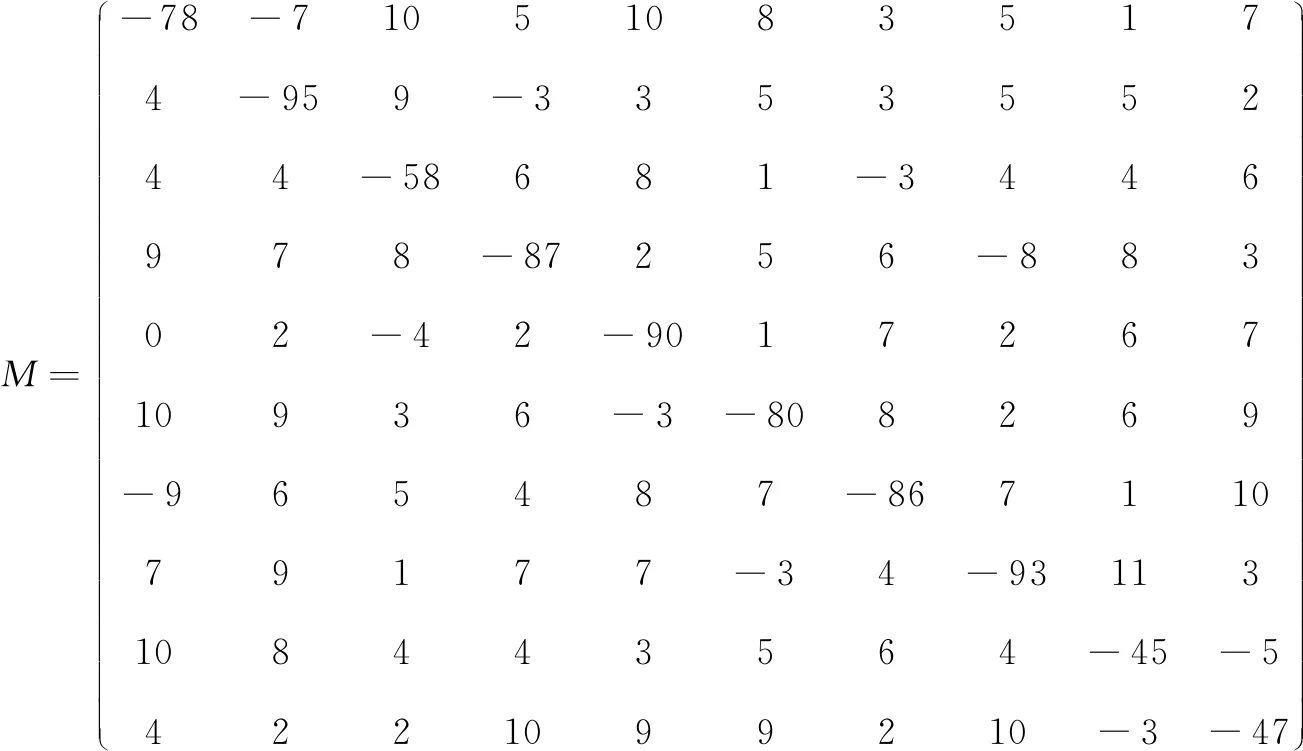
经验证该矩阵是D-Z矩阵，分别运用文献[15]中定理1给出的估计式计算得

运用文献[16]中定理1的估计式计算得

运用本文给出的定理1计算得

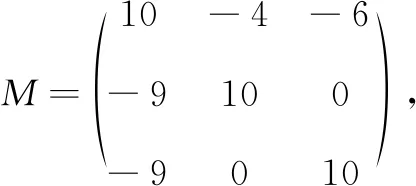
应用文献[7]中的推论1和本文推论2中的估计式分别计算得σ(A)≥5.8527，σ(A)≥4.9146。

4 结束语

从数值算例的计算结果可知，文中给出的新误差界比文献[15]和文献[16]中的更小，说明定理1给出的D-Z矩阵线性互补问题解的误差界优于已有结果，同时推论2中获得的最小奇异值新的下界改进了现有的结论，且计算简单易行，该研究进一步完善了该矩阵类的相关理论知识。