关于对偶对的Gorenstein平坦模及其维数
2020-09-02何东林
何东林, 樊 亮
(陇南师范高等专科学校数信学院, 甘肃 陇南 742500)
引 言
1 定义和引理
设x是一个左R-模类,y是一个右R-模类,M为任意左R-模。
定义1[12]称M是Gorenstein (x,y)-平坦模,如果存在左R-模正合列
X:…→X1→X0→X0→X1→…,
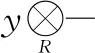
用GF(x,y)表示所有Gorenstein (x,y)-平坦模组成的类。
例1(1)对任意X∈x,有X∈GF(x,y)。
(2)正合列X的每个核、像及余核均是Gorenstein (x,y)-平坦模。
(3)如果x是平坦左R-模类F(R),y是内射右R-模类I(R),则Gorenstein (x,y)-平坦模就是Gorenstein-平坦模。
(4)如果x是平坦左R-模类F(R),那么Gorenstein (x,y)-平坦模与Gorensteiny-平坦模一致。
引理1[12]设GF(x,y)关于扩张封闭,则以下条件等价:


定义2[12]称(x,y)是一个对偶对,如果满足以下条件:
(1)X∈x当且仅当X+∈y,其中X+=HomR(X,Q/Z)。
(2)y关于直和因子和有限直和封闭。
进而,称对偶对(x,y)是完备的,如果R∈x且x关于扩张及直和因子封闭。
引理2[14]如果(x,y)是一个完全对偶对,那么F(R)⊆x且I(R)⊆y。
例2(1)(Fn,In)是一个完备对偶对,其中Fn是平坦维数不超过n的左R-模组成的类,In是平坦维数不超过n的右R-模组成的类。
(2) (Fn,FIn)是一个完备对偶对,其中Fn是FP-内射维数不超过n的右R-模组成的类。
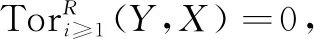
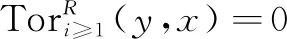
(1)M是Gorenstein (x,y)-平坦模。
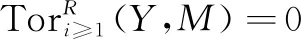
0→M→X0→X1→…,其中Xi∈x。
(3)存在左R-模正合列0→M→X→G→0,其中X∈x且G∈GF(x,y)。
引理4设w是x的余生成子且v是y的生成子,x和y关于扩张封闭,0→M′→M→M″→0是R-模正合列,则以下说法成立:
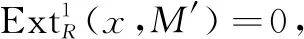

证明由文献[12]中命题3.1易证。
2 主要结果
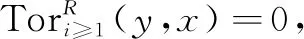


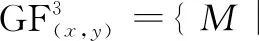
命题2设(x,y)是一个完全对偶对,则以下条件等价:
(i)M是Gorenstein (x,y)-平坦模。
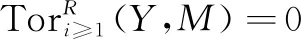
0→M→X0→X1→…,其中Xi∈x。

(v)存在左R-模正合列0→M→X′→G′→0,其中X′∈x且G′∈GF(x,y)。
证明(i)⟺(ii)⟺(v)由引理3易证。
(i)⟹(iv)设M是Gorenstein (x,y)-平坦模,则由定义1知存在左R-模正合列


(1)
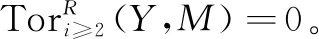

定理1设(x,y)是一个完全对偶对,(ε):0→U→V→W→0是左R-模正合列,则
(i)如果U,W∈GF(x,y),那么V∈GF(x,y)。
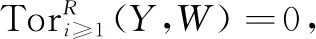
(iii)如果V,W∈GF(x,y),那么U∈GF(x,y)。
证明(i)设U,W∈GF(x,y)。因为GF(x,y)是投射可解的,由文献[12]中命题2.12知,GF(x,y)关于扩张封闭,所以V∈GF(x,y)。
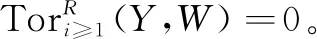
(iii)设V,W∈GF(x,y)。由V是Gorenstein (x,y)-平坦模及命题2可知,存在正合列0→G→X→V→0,其中X∈x且G∈GF(x,y)。构造拉回图,如图1所示。
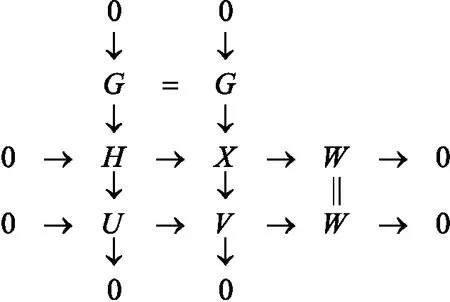
图1 U→V与X→V的拉回图
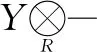
(2)
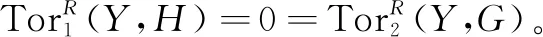
定理2设(x,y)是一个完全对偶对,(ε):0→U→V→W→0是左R-模正合列,则
(i)如果V∈GF(x,y),那么GF(x,y)-pd(W)≤GF(x,y)-pd(U)+1。
(ii)如果U∈GF(x,y),那么GF(x,y)-pd(V)≤GF(x,y)-pd(W)。
证明(i)设V∈GF(x,y)。若GF(x,y)-pd(U)=+∞,则GF(x,y)-pd(W)≤GF(x,y)-pd(U)+1显然成立。若GF(x,y)-pd(U)<+∞,不妨设x-GF(x,y)-pd(U)=n,则存在长度为n的正合列
0→Gn→…→G1→G0→U→0
(3)
其中Gi∈GF(x,y)(i=0,1,…,n)。将式(3)与(ε)拼接可得正合列
0→Gn→…→G1→G0→V→W→0
(4)
其中Gi∈GF(x,y)且V∈GF(x,y)。从而GF(x,y)-pd(W)≤n+1 =GF(x,y)-pd(U)+1。
(ii)设U∈GF(x,y)。若GF(x,y)-pd(W)=+∞,则不等式显然成立。若GF(x,y)-pd(W)<+∞,不妨设GF(x,y)-pd(W)=m,由文献[12]中定理2.16知,存在正合列0→K0→X0→W→0,其中X0∈x且GF(x,y)-pd(K0)=m-1。构造拉回图,如图2所示。
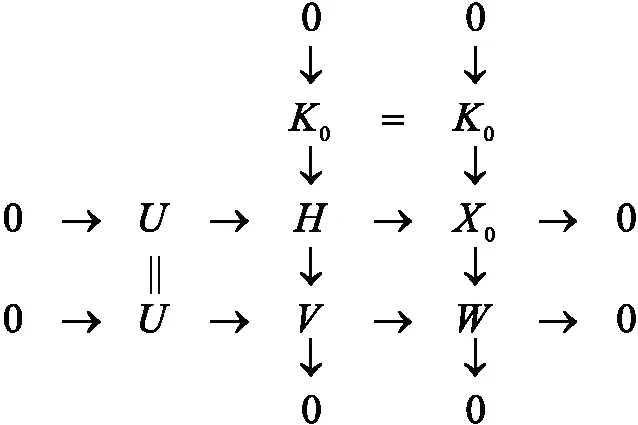
图2 V→W与X0→W的拉回图
在中间行正合列0→U→H→X0→0中,U,X0∈GF(x,y)且GF(x,y)关于扩张封闭,可见H∈GF(x,y)。又因为图2中间列正合列0→K0→H→V→0中,GF(x,y)-pd(K0)=m-1,所以GF(x,y)-pd(V)≤m-1+1=m,即GF(x,y)-pd(V)≤GF(x,y)-pd(W)。
定理3设(x,y)是一个完全对偶对,(ε):0→U→V→W→0是左R-模正合列,如果W∈GF(x,y)且(ε)在HomR(x,-)下正合,那么GF(x,y)-pd(U)=GF(x,y)-pd(V)。
证明设W∈GF(x,y)且(ε)在HomR(x,-)下正合。
先证不等式GF(x,y)-pd(U)≤GF(x,y)-pd(V)。若GF(x,y)-pd(V)=+∞,则不等式显然成立。若GF(x,y)-pd(V)<+∞,不妨设GF(x,y)-pd(V)=n。当n=0时,V是Gorenstein (x,y)-平坦模。由W∈GF(x,y)及定理1可知,U∈GF(x,y)。可见GF(x,y)-pd(U)=0≤GF(x,y)-pd(V),不等式成立。当n≥0时,存在长度为n的正合列
0→Gn→Xn-1→…→X1→X0→V→0
(5)
其中Xi∈x且Gn∈GF(x,y)。令K0=Ker(X0→V),显然GF(x,y)-pd(K0)=n-1。构造拉回图,如图3所示。

图3 U→V与X0→V的拉回图
在正合列0→H→X0→W→0中,X0∈x且W∈GF(x,y),由命题1可得H∈GF(x,y)。考虑图3中第一列正合列0→K0→H→U→0,因为GF(x,y)-pd(K0)=n-1且H∈GF(x,y),所以GF(x,y)-pd(U)≤n-1+1=n,即GF(x,y)-pd(U)≤GF(x,y)-pd(V)。
再证GF(x,y)-pd(V)≤GF(x,y)-pd(U)。若GF(x,y)-pd(U)=+∞,则不等式显然成立。若GF(x,y)-pd(U)<+∞,不妨设GF(x,y)-pd(U)=m。对m用数学归纳法,当m=0时,由GF(x,y)关于扩张封闭易知GF(x,y)-pd(V)=0,可见结论成立。假设结论对于m-1成立,下面讨论对于m的情形。由文献[12]中定理2.16知,存在长度为m的正合列
(6)
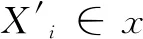
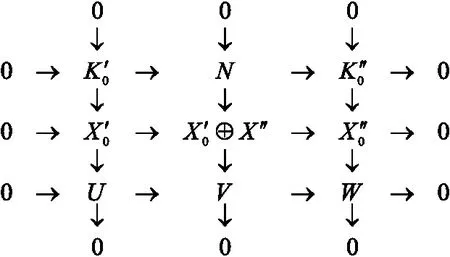
图4 交换图
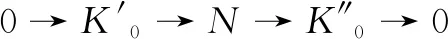
综上所述,GF(x,y)-pd(U)=GF(x,y)-pd(V)。
定理4设(x,y)是一个完全对偶对,则x是GF(x,y)的生成子和余生成子。
证明对任意左R-模M∈GF(x,y),根据定义3可得,存在左R-模正合列
X:…→X1→X0→X0→X1→…,
(7)
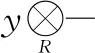
0→M′→X0→M→0和0→M→X0→M″→0,其中X0,X0∈x。又由例1中(2)可知,M′∈GF(x,y)且M″∈GF(x,y)。因此x是GF(x,y)的生成子和余生成子。
推论1设(x,y)是一个完全对偶对,0→M′→M→M″→0是R-模正合列,则
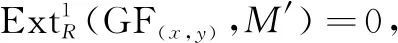
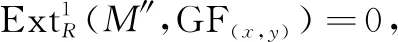
证明根据定理4、引理4以及完备对偶对的定义可证。
3 结束语