优化群分解在磁瓦内部缺陷声振检测中的应用

2020-09-02黄沁元冉茂霞

四川轻化工大学学报(自然科学版) 2020年4期

刘鑫，黄沁元,2，宋弘，冉茂霞，李强

(1.四川轻化工大学自动化与信息工程学院，四川自贡 643000;2.人工智能四川省重点实验室，四川自贡 643000)

引言

磁瓦是一种由铁氧体、铝镍钴等复合材料构成的永磁体，被广泛用于永磁电机中形成恒定磁场。磁瓦作为永磁电机的重要组成部件，其产品质量会直接影响电机的性能和使用寿命。在磁瓦的生产过程中，由于不恰当的温度、压力或人为因素，磁瓦可能会存在裂纹、空隙、夹层、起级等多种内部缺陷问题。这些缺陷对磁瓦的磁通量、剩余磁感应强度、抗过载退磁以及抗老化等产品性能有直接的影响[1]。如果在电机中使用了这些含有缺陷的磁瓦，将会产生不可预估的安全隐患。因此，必须对磁瓦内部缺陷进行可靠的检测，以保证磁瓦的质量和性能。

目前，磁瓦内部的缺陷主要通过人工检测方法来实现，该方法需要将磁瓦从一定高度跌落并撞击金属块来产生声音信号，然后通过人耳对该信号进行辨识，从而判断磁瓦是否存在内部缺陷。人工检测方法受人为因素制约，很难保证稳定的检测效率和检测精度。因此，研究一种自动检测算法并应用于磁瓦内部缺陷检测，具有重要的现实意义和应用价值。在目前无损检测技术中，虽然超声检测、磁粉检测、涡流检测和渗透检测等技术可对物体结构的内部缺陷进行检测，但对于大批量制造的磁瓦来讲难以满足检测速度快、成本低的需求。综合考虑磁瓦检测的特点和需求，声振检测无疑是实现磁瓦内部缺陷检测的一种可行手段[2-4]。

磁瓦与激振块碰撞产生的声音信号，显示出非线性、非高斯和非平稳特征，传统的信号数据处理方法是在信号线性或平稳特性的基础上，将非线性信号转化为线性信号进行处理，因此，不能很好地从复杂非线性信号中提取状态特征。随着信号处理技术的发展，信号的分解方法在机械故障诊断中起着至关重要的作用，受到越来越多研究者的关注。经验模态分解[5]是一种自适应的信号分析方法，可将信号分解为多个模态。然而，经验模态分解方法对噪声敏感，易遭受模态混叠等缺点，限制了经验模态分解在识别机械故障方面的应用。为了解决模态混叠等问题，对经验模态分解进行相应改进的方法被提出，包括集成经验模态分解[6]、带宽经验模态分解[7]等。受经验模态分解方法的启发，自适应信号分解的概念提供了更多的可能性，更多研究者按照这一概念来开发其他自适应信号分解方法，例如局部均值分解[8]、经验小波变换[9]和变分模态分解[10]，这些方法已广泛应用于机械故障诊断领域，并为人们所熟知和接受。

最近，受群智能的启发，利用群滤波(swarm filter，SWF)和迭代算法设计了一种新的信号分解方法[11]，即群分解(swarm decomposition，SWD)。群分解方法借鉴经验模态分解迭代滤波的思想，经过迭代群滤波将原始信号自适应地分解为若干单一模态的振荡分量。群滤波相当于一个带通滤波器，通过调节群滤波参数可以控制振荡分量主模态频率，使得群分解在信号的模态分解方面，可以将频率相近的两个谐波信号分离，相比经验模态分解具有更高的频率区分能力。然而，其阈值需要预先指定，这限制了该方法在机械故障诊断中的应用，难以获得令人满意的结果。为了提高SWD的性能，一种新颖的自然启发式优化算法，即鲸鱼优化算法(whale optimization algorithm，WOA)被提出[12]。WOA具有良好的特性，例如需要控制的参数数量更少，仅依靠一个参数就可以在探索和开发之间平稳过渡，在探索阶段，将根据随机选择的搜索代理找到最佳搜索代理来更新搜索代理的位置。WOA模仿了座头鲸的捕食行为，在文献[12]中论证了它的全局优化性能，已被广泛应用于解决工业领域中优化问题。文献[13]提出使用WOA寻找最优特征子集，该子集可最大程度地提高分类的准确性，同时保留最少数量的特征。文献[14]针对太阳能电池的参数估计问题，应用WOA来自动调整优化算法的内部参数。

得益于SWD和WOA的优点，提出使用WOA对磁瓦声振信号的SWD分解参数进行优化，从SWD分解得到的一系列分量中筛选出特征分量，并提取故障信息，进而对磁瓦内部是否含有缺陷进行判别，为解决磁瓦内部缺陷检测问题提供新的方案。

1 基础理论

1.1 群分解

SWD作为一种智能的分解方法，在正确参数化SWF的基础上，从多分量信号中迭代提取主振荡分量(oscillatory component，OC)。关于SWD分解的详细描述参考文献[11]。当使用SWD对信号进行分解时，算法流程可以总结为：

(1)

其中：Sx(ω)表示韦尔奇功率谱，q表示在执行SWD分解过程中第q次作为中心频率。

(2)

(3)

(3) 对输入信号进行离散化：xit[n]←x[n]，xit[n]为离散数据序列，it为序号。设置it=0，并指定y0[n]←xit[n]。

(4)j=1时，对x[n]进行SWF滤波[11]：

yj[n]←SWF(xit[n],M,δ)

(4)

(5) 计算迭代偏差StD：

(5)

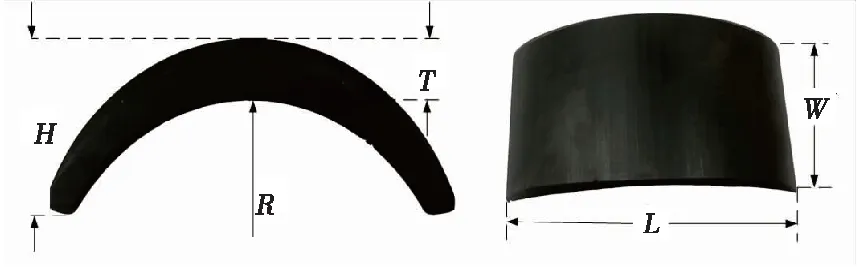
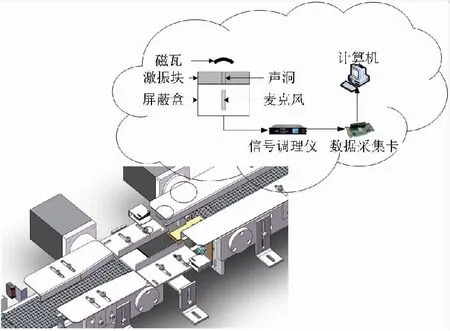
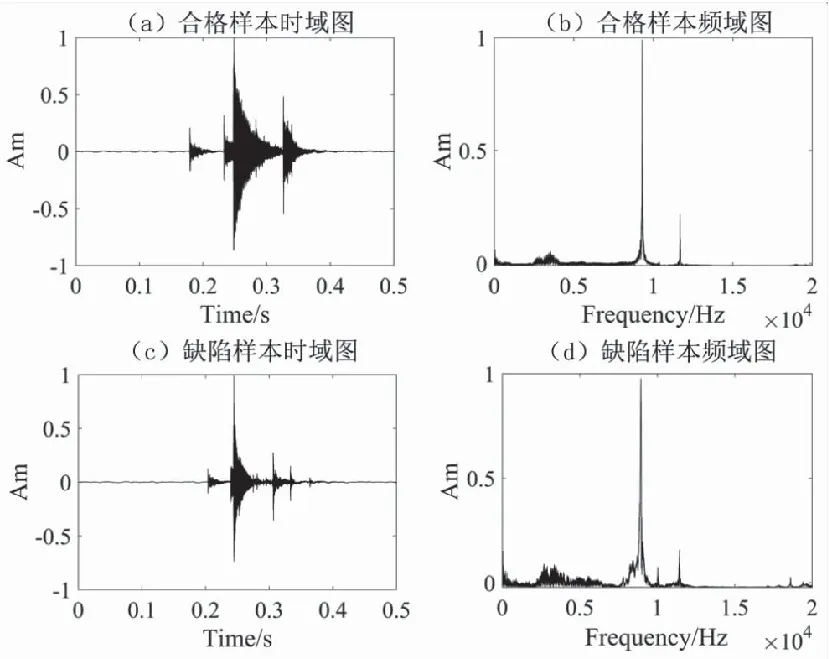
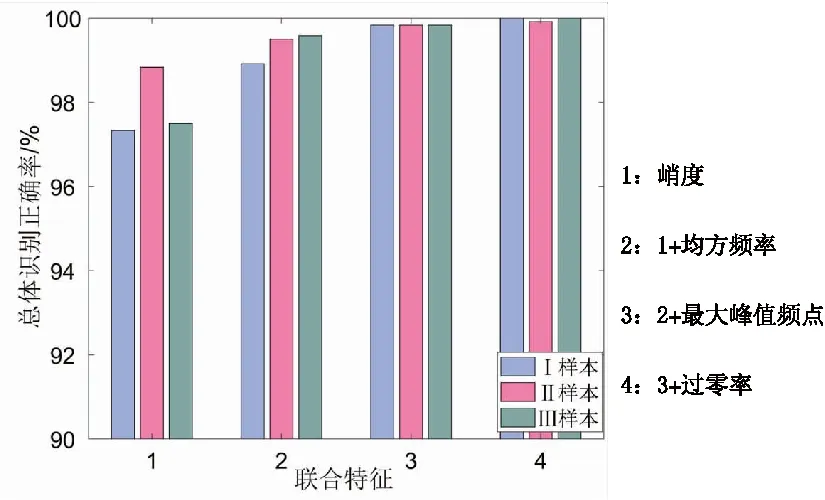
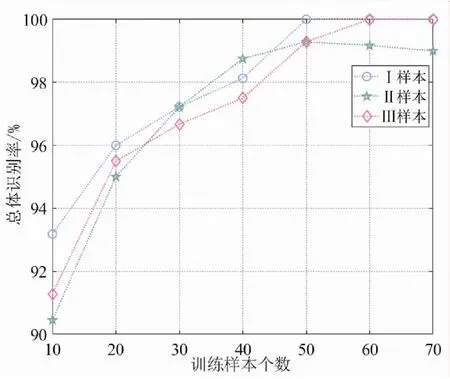
(6) 当Sx

(6)

否则，用xit+1[n]重复步骤(3)。

值得注意的是，不同阈值的SWD分解会得到不同的模态分量，而这些模态分量不一定适合用于故障识别和检测。这问题主要归因于阈值Pth和StDth的选择，这对于该分解方法的性能而言非常重要，它们可以控制分解过程结束时提取的振荡分量的数量。事实上，较小的阈值意味着更多的振荡分量和复杂的分解，但并不意味着更好的结果，同时，这需要耗费大量的计算，文献[11]建议将两个阈值设置为0.1，但是这个取值并非适合每一个磁瓦声振信号。因此，对于SWD而言，如何确定SWD的阈值非常重要。目前而言，WOA的阈值的选择阻碍了其广泛应用于机械故障振动信号分析[15]。为了解决这一瓶颈，本文提出了优化群分解，得益于WOA的优点并结合适当的优化准则，即使在不同的情况下，也可以找到适当的阈值，并利用SWD从复杂的多分量信号中分离并提取故障信息。

1.2 鲸鱼优化算法

WOA主要模拟座头鲸捕食的过程，从而提出的一种新的智能优化算法。座头鲸的捕食过程可以概括为三种行为：包围猎物、气泡网攻击以及搜寻猎物。

(1) 包围猎物

一旦发现猎物的位置，捕猎的第一步就是将其包围起来，该行为的数学模型如下：

D=|C·X*(t)-X(t)|

(7)

X(t+1)=X*(t)-A·D

(8)

其中：X*是目前得到的最佳解的位置向量，X是座头鲸的位置向量；A和C表示系数；t表示当前为第几次迭代。为了得到最佳解，鲸鱼的位置按照下列等式在每次迭代时进行更新：

A=2a·r-a

(9)

C=2·r

(10)

其中：r是[0,1]之间的随机向量；a在迭代过程中从2到0线性减小。

(2) 气泡网攻击

气泡网攻击法是一种仅在座头鲸中观察到的独特的狩猎方法，为了建立该行为的数学模型，设计了两种方法。

第一种称为收缩包围机制，该行为是通过减小式(8)中A的值来实现的。A的取值范围为[-a,a]，它的改变是通过减小a来实现。将A设为[-1,1]中的任意值，当0≤A≤1时，鲸鱼将攻击猎物。

第二种是螺旋更新位置，根据鲸鱼和猎物的位置生成一个螺旋方程，以模拟鲸鱼的螺旋状运动：

X(t+1)=D′·ebg·cos(2πg)+X*(t)

(11)

其中：D′=|X*(t)-X(t)|，表示鲸鱼与猎物之间的距离；b是一个常数，用来模拟对数螺线的形状；g是一个[-1,1]之间的变量。

为了模拟气泡网攻击，各有50%的概率选择上面方法之一来更新鲸鱼的位置，因此，数学模型为：

(12)

其中：p是[0,1]之间的随机值。

(3) 搜寻猎物

实际上，鲸鱼需要依靠彼此的位置来随机寻找猎物。A为随机值，当|A|>1时，搜寻代理被迫远离参考鲸鱼。下面的算子可以进一步提高WOA算法的全局优化性能：

D=|C·Xrandom(t)-X(t)|

(13)

X(t+1)=Xrandom-A·D

(14)

1.3 随机森林

RF算法是一种集成分类方法[16]，其基于训练集的引导样本应用bagging方法创建多个决策树，一个RF模型通过平均其成员树的决策来获得分类。训练集的一个引导样本可以独立构造一棵树，并可从预测变量的随机子集中选择每个节点的最佳分割，确保了在每棵树上以不同方式构造训练集和预测变量。RF的最终结果是通过统一投票获得的，获得最高票数的未标记数据是弱学习者的输出结果。

RF作为一种组合分类模型，由许多分类树模型组成：{h(X,θk),k=1,...,N}，其中变量集θk是独立同分布的随机向量，X是独立输入向量。一个树分类器h(X,θk)是基于训练集X和变量集θk构建的，每棵树都有一票选择最佳分类结果。根据不同训练集，RF可构建彼此差异的分类模型，以此提高组合分类模型的预测能力。经过k次训练，一个多分类模型系统{h1(X),h2(X),...,hk(X)}就可以得到。通过简单的多数投票可得最终分类结果，最终分类决策表示如下：

(15)

其中：H(x)是组合分类模型；hi是单个决策时模型；Y是hi(X)的输出变量。

2 检测方法与实验流程

2.1 实验样本

所有的实验样本都是由铁氧体材料制成，每一个样本都通过经验丰富的检验人员认定，以确定磁瓦是否存在内部缺陷。具有内部缺陷的样本标识为缺陷样本，其他标识为合格样本。根据样本的大小，将其分为三种类型(Ⅰ、Ⅱ和Ⅲ)，三种样本在尺寸上分别代表了大、中、小磁瓦，其产量和销量都比较高，因而较具有代表性。每种类型样本都有240片，合格与缺陷各有120片，磁瓦的示意图如图1所示，R为磁瓦半径，H为磁瓦高度，T为磁瓦厚度，L和W分别为磁瓦的长度和宽度。此外，根据用途的不同，每种类型又分为训练样本与测试样本两组，每组包含一定数量的合格和缺陷样本，用以验证所提方法的可行性。四种磁瓦样本的尺寸、数量和用途信息见表1。

图1 磁瓦结构示意图

表1 实验样本信息

2.2 声振信号采集

实验的目的是利用声振检测实现对合格样本和缺陷样本的自动分类，其中声振信号的获取和分析是实验的关键。磁瓦声振信号采集系统如图2所示，左下部分是磁瓦检测装置的结构示意图，屏蔽盒位于激振块的下方，右上部分为声音信号采集系统简化图。首先，为了产生声音信号，每个样本都从20 mm的高度跌落，与激振块碰撞。值得注意的是，合格磁瓦不会产生新的缺陷。声音信号激发的同时，麦克风就将其转化为电信号。考虑到环境噪声的影响，麦克风被安置在由隔音材料制成的屏蔽盒内，激振块位于屏蔽盒的顶端，且激振块中部有一直径2 mm的声洞。这样，能在较好地隔绝噪声影响的同时有效地传递声振信号。声振信号经信号调理仪放大滤波再由数据采集卡采集并存入计算机。

图2 磁瓦声振信号采集系统

2.3 实验流程

本文提出的磁瓦内部缺陷声振检测法整体流程如图3所示，具体过程为：

图3 算法整体流程

(1) 针对预先指定SWD的分解参数Pth和StDth，每个样本的声振信号SWD分解效果不能达到最佳的问题，在合适的优化准则下，利用WOA对SWD的分解参数进行优化。

(2) 利用获得的最优分解参数对每个磁瓦声振信号进行SWD分解，得到SWD的多个振荡分量。

(3) 计算分解得到的振荡分量的能量，选取能量最大者作为特征分量。

(4) 计算特征分量的峭度、均方频率、最大峰值频点和过零率，作为内部缺陷存在与否的联合描述，构建每个信号的特征数据向量。

(5) 将每类样本的特征量分为训练样本和测试样本，训练样本用作训练RF，并建立具有识别磁瓦内部缺陷功能的分类器，测试样本用作验证训练好的RF分类器的识别性能。

3 实验结果及分析

3.1 SWD参数优化

文献[17]已经提到，WOA进行寻优是通过使适应度函数值最小来完成的，为了保证优化算法的高效率和高准确性，一个简单且稳定的优化准则尤其重要。本文采用唐贵基[18]提出的包络熵，用于评定SWD分解结果的优劣。包络熵Eq表示为：

(16)

其中：N为信号的长度；qn为a(n)的归一化形式；a(n)为振荡分量经Hilbert解调后得到的包络信号。包络熵是信号稀疏特性的一种反应形式，信号的稀疏性越强，包络熵越小，反之，信号稀疏性越弱，包络熵越大。利用SWD对磁瓦声振信号处理得到一系列振荡分量，如果振荡分量中含有较多的噪声分量，信号的稀疏性较差，则信号的包络熵较大。因此，以振荡分量的局部包络熵值最小化为寻优目标，即适应度函数为：

fit=min(Eq)

(17)

SWD分解参数的寻优过程如下：

(1) 初始化鲸鱼数量、最大迭代次数和其余WOA算法的参数a、A、C和p，并设置SWD分解参数的范围。

(2) 根据鲸鱼所在位置的坐标为SWD分解的参数对磁瓦声振信号进行分解，得到一系列振荡分量。

(3) 以优化准则计算所有振荡分量的包络熵值，得到局部最小包络熵值，并设置对应的鲸鱼为最佳搜寻代理X*。

(4) 如果p<0.5，当|A|<1按照式(8)更新当前鲸鱼的位置，当|A|≥1按照式(14)更新当前鲸鱼的位置；如果p≥0.5，则按照式(11)更新鲸鱼的位置。

(5) 更新参数a、A、C和p的值。

(6) 确定当前迭代次数t是否小于最大迭代次数，如果是，重复步骤(2)～步骤(5)，否则得到最佳搜寻代理X*，最佳搜寻代理的位置坐标即为最终SWD寻优参数的取值。

为了验证WOA的性能，在样本Ⅱ中随机抽取一个合格样本的声振信号进行SWD参数寻优，将鲸鱼数量设置为20，最大迭代次数设置为10，随着WOA迭代次数的增，寻优路径如图4所示。从图4可以看出，随着迭代次数的增加，搜寻位置对应的参数在不断变化，其对应的适应度函数值逐渐减小，当找到全局最小值后不再变化。即WOA算法能够准确找到适应度函数的全局最小值，即确定SWD参数的最优值。

图4 WOA寻优结果

既提高检测方法的效率，又保证SWD方法分解精度的同时，在每类样本中，取合格与缺陷磁瓦声振信号各10个，利用WOA算法进行参数寻优。取20组参数的平均值作为这一样本类型的SWD分解参数，各类样本的参数设置见表2。

表2 SWD参数设置

3.2 声振信号SWD分解

对磁瓦声振信号进行群分解是其内部缺陷检测的关键一步。以样本Ⅱ中的声振信号为例，采样周期为0.5 s，采样频率为40 kHz，合格与缺陷磁瓦声振信号的时域、频域波形图如图5所示。从图5可以看出，合格与缺陷磁瓦的特征毫无规律性，无法直观提取有关内部缺陷的特征。限于篇幅，仅以合格磁瓦声振信号为例，将传统的集合经验模态分解(ensemble empirical mode decomposition，EEMD)作为对比，验证SWD算法在信号分解方面的优势。

图5 合格与缺陷磁瓦声振信号

为了直观地表示信号分解效果，对SWD和EEMD分解得到的模态分量分别进行频谱分析，分别如图6和图7所示，限于篇幅，图7中EEMD谱仅展示了前5个模态的频谱。从EEMD频谱可以看出，EEMD分解磁瓦声振信号时，出现较严重的模态混叠现象，一个模态分量含有多个频段成分。而经SWD分解处理获得的模态分量的中心频率相互独立，信号得到有效分解，优势显著。

图6 合格磁瓦声振信号SWD频谱

图7 合格磁瓦声振信号EEMD频谱

3.3 特征提取

利用WOA优化得到的SWD分解参数对磁瓦声振信号进行分解后，得到一定数量的振荡分量，这些分量都或多或少包含着有关内部缺陷的特征信息。利用振荡分量的能量大小筛选特征分量能简化数据处理并提高特征提取的有效性。从筛选出的特征分量中提取有效特征对磁瓦内部缺陷的识别起着至关重要。由于单个或单域特征难以全面准确反映出磁瓦内部缺陷，因此从特征分量中提取时域、频域特征，构建混合域特征集可以较为有效反映出磁瓦内部是否存在缺陷。具体特征信息如下：

(1) 峭度[19]：反映随机变量的分布特性的数值统计量，对信号中的冲击特性较为敏感，经实验发现，内部缺陷磁瓦声振信号的峭度一般大于合格磁瓦声振信号的峭度。信号x[n]的峭度为：

(18)

其中：μ是x[n]平均值，σ为x[n]的标准差，E(·)表示期望值。

(2) 均方频率[19]：描述功率谱主频带位置的变化，其计算公式为：

(19)

其中：s(f)为信号的功率谱，f为信号频点序号。

(3) 最大峰值频点：特征分量在快速傅里叶变换下可得到其频谱，频谱中最大峰值频点代表了磁瓦声振信号的振动频率，与磁瓦的物理结构有直接关联，能够作为区别合格与缺陷磁瓦的特征。

(4) 过零率[20]：计算信号穿越时间轴的次数，在一定程度上反映频谱的性质，表现为周期成分多时小，噪声成分多时大。计算公式为：

(20)

其中：N表示信号的长度，sgn(·)表示符号函数，即：

(21)

提取的4类特征的对比如图8所示。联合特征的识别正确率如图9所示，横坐标表示联合特征的个数，从单特征来看，虽然合格样本与缺陷样本在单个特征上具有一定的区分，但取单特征作为识别合格与缺陷磁瓦的特征，缺陷识别准确率不能满足检验精度。对比多个联合特征的识别正确率，将4个特征组合，作为识别缺陷与合格磁瓦的联合特征，满足磁瓦缺陷检测的精度要求。因此，联合峭度、均方频率、最大峰值频点和过零率这4个特征，作为识别缺陷与合格磁瓦的特征，达到磁瓦缺陷检测的目标。

图8 4类特征统计结果

图9 联合特征对识别正确率的影响

3.4 缺陷识别

提取有效特征后，便需要合适的分类器进行缺陷识别，用以确定样本是否为缺陷磁瓦。本文主要利用RF作为分类器，并使用k最近邻(k-nearest neighbor，KNN)和支持向量机(support vector machine，SVM)作为对比，以验证整个磁瓦内部缺陷检测方法的有效性。在实际生产中，为了保证只有经检测合格的磁瓦被用于电机等产品中，因此要求设计的检测方法对缺陷样本的识别正确率为100%。

SWD的参数优化对磁瓦缺陷识别正确率的影响如图10所示。为了简化，在设定SWD参数时，两参数取值一样，且跨越整个参数可取值的范围。虽然未优化参数时，也存在总体识别正确率超过98%，但其未能对缺陷样本做出100%识别，不能满足实际检测需求。对SWD的参数取值进行寻优后，不仅能对缺陷样本100%识别，而且总体识别正确率也是最高的。

图10 SWD参数优化对识别正确率的影响

分类器的识别能力得益于训练样本的训练效果，由于训练样本仅提供有无缺陷信息，因而对于识别能力的影响主要体现在训练样本的数量上。一般认为训练样本的数量越多，分类器的训练效果越好，但过多的训练样本数量容易引起重复训练，降低缺陷识别的效率。

训练样本由等量的合格与缺陷样本组成，训练样本个数对总体识别正确率的影响如图11所示。从图11可以看出，训练样本中合格与缺陷样本的个数增加时，3类样本的总体识别正确率逐渐递增，当训练样本个数为60时，Ⅰ样本、Ⅱ样本、Ⅲ样本的识别正确率达到识别准确的最佳值，分别为100%，99.17%和100%，满足实际检测需求。因此训练样本的数量确定为合格与缺陷样本各60，对于获得最佳识别正确率是合理的。

图11 训练样本个数对识别正确率的影响

确定合理的训练样本数量后，可根据测试样本的识别正确率来检验不同分类器的识别能力，表3展示了RF、KNN和SVM 3种分类器对磁瓦内部缺陷的识别效果。3种分类器的参数设置如下：RF中将树的数量nBag取50；KNN中，k值为5，距离函数为euclidean；SVM中，惩罚参数c为2，核函数参数γ为1。从表3可以看出，仅RF分类器满足检测要求，对3类样本中含有内部缺陷的磁瓦识别正确率为100%，对Ⅰ、Ⅱ、Ⅲ样本中合格磁瓦识别正确率分别为100%、98.33%和100%。