基于宽频电阻抗特性与阿尔奇公式的含水合物饱和度计算模型

牛佳乐，邢兰昌，魏 伟，韩维峰，曹胜昌

(1.中国石油大学(华东) 控制科学与工程学院，山东 青岛 266580；2.中国石油勘探开发研究院 新能源研究所，河北 廊坊 065007)

0 引言

天然气水合物是由一种或几种烃类气体和水组成的结晶状物质，自然界中水合物广泛分布在海底浅层沉积物以及陆上冻土带，其中海域水合物资源量占我国水合物总资源量的90%以上[1-2]。因天然气水合物具有巨大的地质储量和清洁无污染的特点，已成为一种重要的战略能源和潜在的未来资源[3-5]。

含水合物饱和度的评价是天然气水合物资源储量估算、勘探开发的关键问题之一。由于天然气水合物电阻率极高，当沉积物中的部分孔隙水被水合物取代时，沉积物电阻率会显著增大，理论和实践表明可以根据沉积物电阻率来估算含水合物饱和度[6-8]。Spangenberg等[9]测量了甲烷水合物在玻璃珠表面生成过程中的电阻率变化，发现阿尔奇公式中的电阻率增大指数与水合物饱和度在双对数坐标系下存在非线性关系。Lee等[10]测量了含四氢呋喃水合物的砂、泥沙和黏土的电阻率，结果表明电阻率显著反映含水合物饱和度的变化，但是会受到微观分布模式等其他因素的影响。陈玉凤等[11]测量了南海沉积物内甲烷水合物形成过程中的电阻率并利用阿尔奇公式建立电阻率与含水合物饱和度之间的关系，结果表明饱和度指数随含水合物饱和度变化而变化。上述研究显示由于受到沉积物的组分、水合物微观分布模式、孔隙水矿化度等因素的影响，基于电阻率数据并利用阿尔奇公式进行含水合物饱和度计算时遇到挑战。

含水合物沉积物电学性质较为复杂且影响因素众多，单一频率条件下测试得到的电阻率数据信息量有限，忽略了被测介质的电容性和频散特性。交流阻抗法测试频率范围宽，能够获得被测介质的阻抗值，因此有望更加全面地刻画含水合物沉积物的电学特性[12-13]。邢兰昌等[12]测试了四氢呋喃(THF)水合物的生成和分解过程的阻抗谱，在建立阻抗谱等效电路模型的基础上分析了电路元件参数的变化规律。金学彬等[14]对含甲烷水合物的天然海沙进行了阻抗谱测试，结果表明特定测试频率下的阻抗幅值与含水合物饱和度之间呈现近似线性关系。针对冻土区天然气水合物储层的特点，李栋梁等[15]利用模拟混合气合成含水合物砂岩样品，在1～200 kHz频率范围内测试了样品的电阻和电容，分别讨论了水合物形成对岩芯电阻率和介电常数的影响规律。王彩程等[16]在对含甲烷水合物的天然海砂体系进行阻抗谱测试的基础上探讨了含水合物饱和度对复电阻率频散特性的影响规律，建立了描述该复杂体系的复电阻率模型，利用该模型可以求解含水合物饱和度，但是模型的数值求解算法需要进一步研究。

本文利用自主设计开发的水合物电学参数测量装置在宽频率范围(5 Hz～400 kHz)内对含四氢呋喃(THF)水合物海沙体系进行了实验测试，分析了含水合物模拟沉积物宽频阻抗特性，并建立了基于宽频阻抗幅值和阿尔奇公式的含水合物饱和度实用计算模型，为沉积物中含水合物饱和度的评价提供了新的测试与计算方法。

1 实验装置与测量

1.1 实验装置

四氢呋喃(THF)在常压下呈液态，可与水以任意比例互溶，在常压下4.4 ℃时即可生成与天然气水合物性质相似的水合物，无需高压装置，实验相对简单安全[17]，因此本文以THF水合物为研究对象开展模拟实验与测试。所采用的实验装置为自主设计开发的THF水合物电学参数测量装置[18]，其结构如图1所示。该测量装置主要由反应釜﹑低温箱﹑电学测量系统﹑温度测量系统和工控机及测控软件组成。

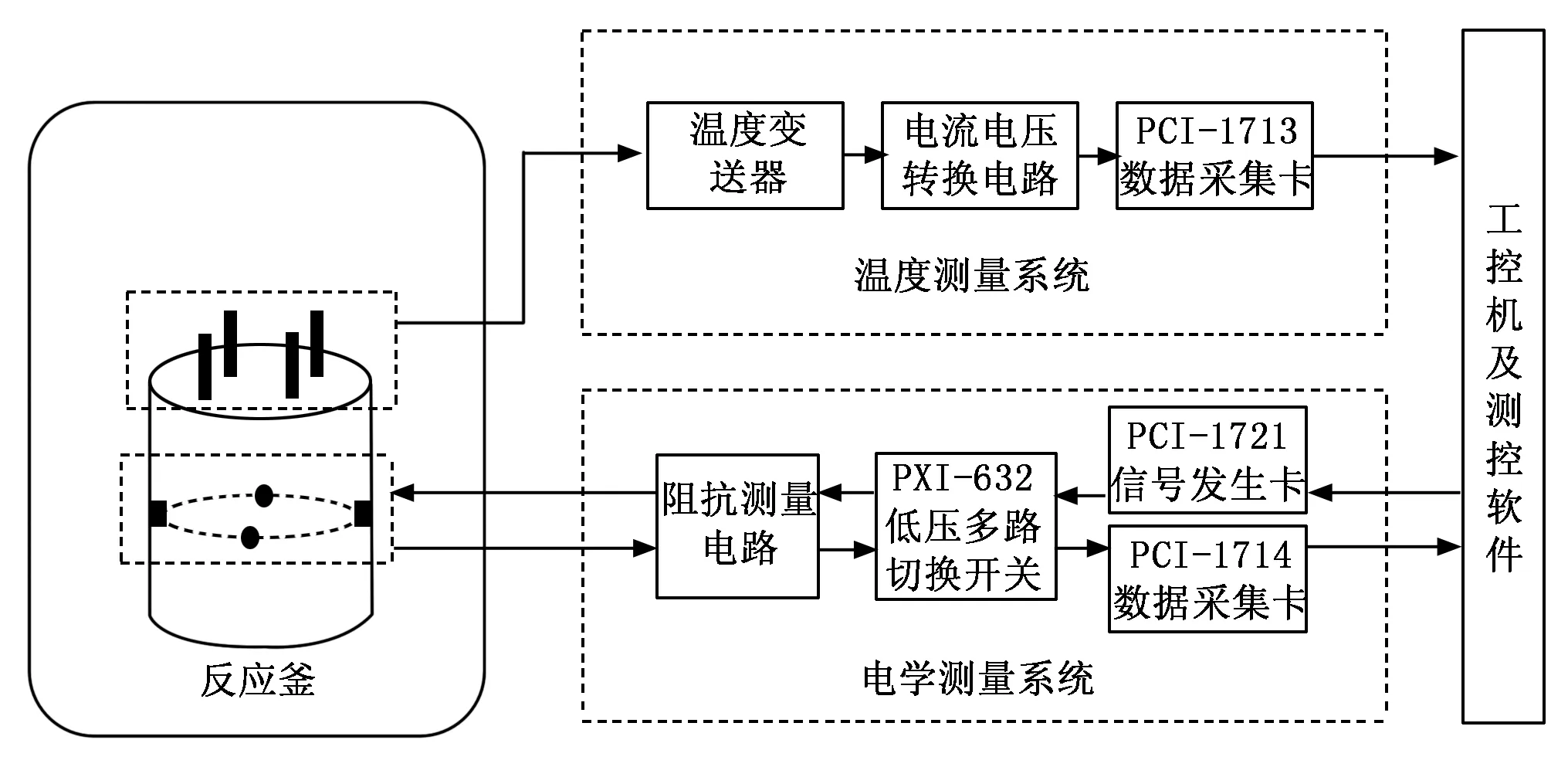
图1 实验装置总体结构

反应釜的材料为聚四氟乙烯，具有良好的耐腐蚀性。电学传感器为4个电极，均匀分布在反应釜四周；测温元件为Pt100热电阻，其测温精度为A级，通过反应釜盖插入反应釜内。采用PCI-1721信号发生卡输出5～500 kHz的正弦波来激励电学传感器；PCI-1714数据采集卡用于采集阻抗测量电路的电压信号；PXI-632低压多路切换开关用于电学传感器工作模式的切换。热电阻温度变送器输出标准的4～20 mA电流信号，进一步转换为1～5 V的电压信号后由PCI-1714数据采集卡采集。工控机及测控软件实现对整个装置的控制、对数据进行处理与显示。

1.2 传感器工作模式

电极在反应釜壁上的分布如图2所示，其工作模式设定如下：

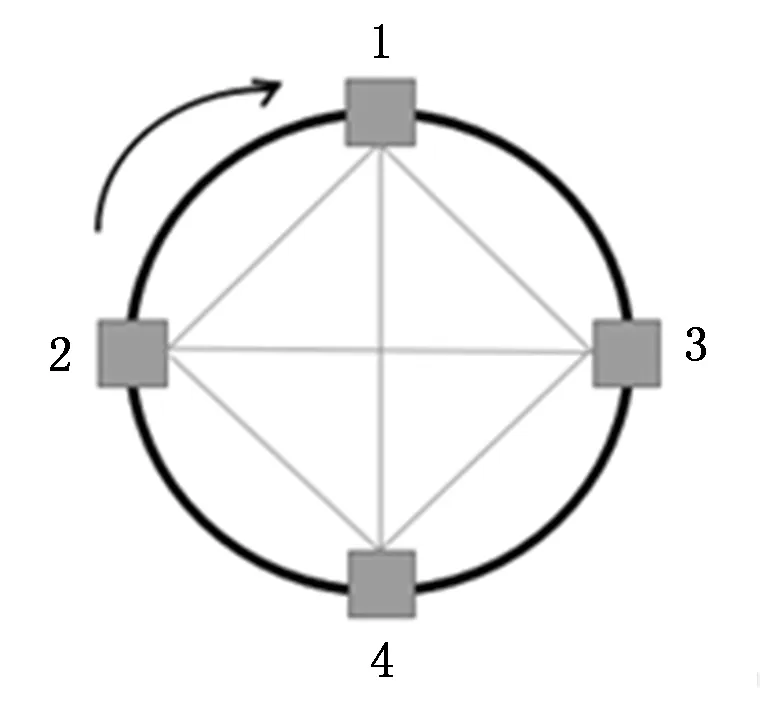
图2 电学传感器工作模式图

1)将1号电极依次与2号﹑3号和4号电极形成工作电极对，测量各电极对间的阻抗值。

2)将2号电极依次与1号﹑3号和4号电极形成工作电极对，测量各电极对间的阻抗值。

3)将3号电极依次与1号﹑2号和4号电极形成工作电极对，测量各电极对间的阻抗值。

4)将4号电极依次与1号﹑2号和3号电极形成工作电极对，测量各电极对间的阻抗值。

5)设置激励信号的频率为21个频率点：5 Hz、6 Hz、10 Hz、20 Hz、40Hz、60 Hz、100 Hz、200 Hz、400 Hz、600 Hz、1 kHz、2 kHz、4 kHz、6 kHz、10 kHz、20 kHz、40kHz、60 kHz、100 kHz、200 kHz、400 kHz。

1.3 实验步骤

1)对天然海沙进行筛选﹑漂洗﹑烘干，然后称取650 mL的60～80目的海沙装入反应釜内待用。

2)按照实验所需THF水合物饱和度分别计算THF和蒸馏水的质量，按照质量分数1%计算所需NaCl的质量。

3)用电子天平分别称取蒸馏水﹑THF和NaCl，并将三者混合搅拌，使其充分互溶。

4)将搅拌均匀的混合溶液缓慢倒入反应釜内，并用玻璃棒搅拌，使溶液充分填满孔隙，然后静置反应釜24小时。

5)待反应釜静置完毕后，将反应釜放入低温箱，设定温度为-1.5 ℃，开启测控软件，对THF水合物的降温生成过程进行测试。

6)THF水合物完全生成后，关闭恒温箱，对THF水合物的升温分解过程进行测试。

2 含水合物模拟沉积物宽频阻抗特性

2.1 THF水合物饱和度计算

实验中在保证THF水合物完全生成的条件下，海沙中含水合物饱和度可以通过THF与蒸馏水的配比来计算[19]。已知THF水合物的分子式为8C4H8O·136H2O，即每生成1 mol的THF水合物，需要消耗1 mol的THF和17 mol的H2O。设初始状态下水和THF的体积分别为VW和VTHF，水和THF的密度分别为ρw=1 g/cm3和ρTHF=0.888 g/cm3，水和THF的摩尔质量分别为MW=18 g/mol和MTHF=72.11 g/mol，海沙中THF水合物饱和度为Sh，则THF水合物完全生成后其物质的量nTHF为(海沙孔隙中存在剩余水)：

(1)

剩余水的饱和度为：

(2)

化简后得到THF水合物饱和度计算公式：

(3)

2.2 水合物生成分解过程的阻抗变化特性

图3为THF水合物饱和度为60%时，其生成分解过程中电极之间的阻抗幅值和温度随实验进程的推进而变化的曲线，结合温度变化曲线可以将整个实验过程划分为7个阶段。

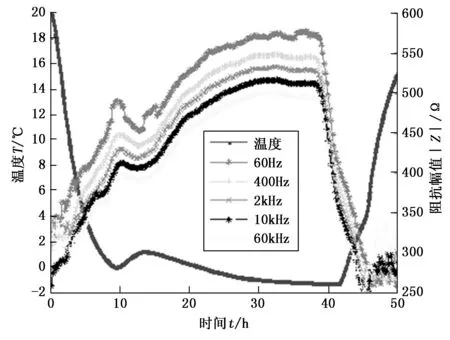
图3 水合物生成分解过程阻抗幅值和温度变化曲线

第一阶段为降温水合物未生成阶段(0～10 h)，反应釜内模拟沉积物的温度从20 ℃降低至0 ℃，400 Hz频率下的阻抗幅值从300 Ω增大到450 Ω。温度下降降低了孔隙溶液中导电离子的活性，导电离子在外加电场作用下定向迁移速度降低，则被测介质阻抗幅值呈现增大的趋势。

第二阶段为水合物生成初期阶段(10～14 h)，此阶段内水合物开始生成，模拟沉积物温度从0 ℃升高至1 ℃(放热效应)，400 Hz频率下的阻抗幅值从450 Ω减小到440 Ω。当温度减低到相平衡温度以下并持续一段时间后，THF水合物会在孔隙中逐渐生成，消耗孔隙水使得孔隙水中的离子浓度增大(排盐效应)，导致被测介质的阻抗幅值减小。

第三阶段为水合物持续生成阶段(14～25 h)，此阶段内水合物持续生成至所有的THF转化为水合物，400 Hz频率下的阻抗幅值从440 Ω增大到530 Ω。随着THF水合物生成量的增加，水合物对孔隙的堵塞作用增强，被测介质的阻抗幅值增大。

第四阶段为温度稳定阶段(25～39 h)，模拟沉积物温度逐渐降低至-1.5 ℃(设定温度)并稳定，400 Hz频率下的阻抗幅值从530 Ω增大到550 Ω。水合物完全生成后，温度的降低导致阻抗幅值略有增大。

第五阶段为升温水合物未分解阶段(39～44 h)，模拟沉积物温度从-1℃升高至3℃(低于相平衡温度)，水合物尚未分解，此阶段400 Hz频率下的阻抗幅值从550 Ω减小到350 Ω。温度的升高提高了孔隙溶液中导电离子的活性，导电离子在外加电场作用下定向迁移速度增大，则被测介质的阻抗幅值减小。

第六阶段为水合物分解阶段(44～46 h)，模拟沉积物温度从3 ℃升高至4～5 ℃(高于相平衡温度)，THF水合物开始分解，此阶段400 Hz频率下的阻抗幅值从350 Ω减小到250 Ω。随着水合物的分解，其水合物对孔隙的堵塞作用减弱，阻抗幅值减小。

第七阶段为持续升温阶段(46～50 h)，此阶段内，模拟沉积物的温度从5 ℃升高至16 ℃，被测介质阻抗幅值主要受温度影响，400 Hz频率下的阻抗幅值从270 Ω减小到250 Ω。

图4给出了测试频率为60 Hz时通过3组电极对得到的阻抗幅值随时间变化的曲线。由图可知，在水合物生成分解过程中，3组阻抗幅值的变化趋势一致，而且量值接近，其中3者最大差值为25 Ω，占该时刻平均幅值的4.5%。由于THF溶液与水可以任意比例互溶，即配置的混合溶液组分均匀，且填沙过程中注意将溶液均匀饱和于海沙孔隙中，所以在水合物生成分解过程中反应釜内水合物空间分布较为均匀，不同位置处的含水合物饱和度接近。

图4 不同电极对的阻抗幅值曲线

2.3 阻抗频散特性与水合物饱和度的关系

图5为在5 Hz～400 kHz频率范围内THF水合物饱和度不同时模拟沉积物阻抗幅值随频率变化的曲线。由图可知：阻抗幅值随着测试频率的增大而减小。分析原因如下：1)在外加电场作用下，多孔介质孔隙流体中原来达到平衡状态的离子会重新分布在孔隙壁的表面，阳离子顺着电场方向移动，阴离子逆着电场方向运动，同时孔隙壁也会感生出束缚电荷，使得孔隙流体中的导电离子堆积在孔隙壁上，孔隙壁与流体界面产生界面极化效应[20]，频率越低容抗越大；2)随着测试频率的增大，界面极化效应逐渐减弱，孔隙壁对孔隙流体中导电离子的束缚能力变弱，容抗减小继而导致阻抗幅值减小。

图5 含水合物模拟沉积物阻抗幅值频散曲线

为了定量分析含水合物饱和度对阻抗幅值频散特性的影响，将0.1 kHz和10 kHz的阻抗幅值分别记为低频和高频幅值(实际计算时，高频点与低频点可适当选取)，按照式(4)计算不同饱和度阻抗幅值的频散度[16,21]。

④在流域内部同一区域还存在地州与兵团师不同隶属关系、自成体系的两套水资源管理体制，存在着各自为政、分割管理的问题。

(4)

式中,|Z|PFE为阻抗幅值频散度；|Z|L为低频阻抗幅值；|Z|H为高频阻抗幅值。

图6所示为阻抗幅值频散度与含水合物饱和度的关系图。由图可知，在实验条件下阻抗幅值频散度随着含水合物饱和度的增大而逐渐减小，而且两者呈现出近似线性关系，因而可以将频散度作为特征参数来估算含水合物饱和度的大小，其表达式为：

|Z|PFE=-0.35Sh+0.43

(5)

3 基于阿尔奇公式的含水合物饱和度模型

通过上述分析可知，模拟沉积物的阻抗幅值与含水合物饱和度之间存在密切的关系，并且受到频率的影响，因此考虑建立不同频率下阻抗幅值与含水合物饱和度之间的定量关系模型，即含水合物饱和度计算模型。

阿尔奇公式描述了多孔介质电阻率﹑孔隙度与含水饱和度之间的关系，可以表示为以下两个表达式[22]：

(6)

式中,F为地层因子，Ro为饱和水多孔介质电阻率，Rw为孔隙水电阻率，φ为多孔介质的孔隙度，a为岩性系数，m为胶结指数。

(7)

式中,I为电阻率增大指数，Rt为含水多孔介质的电阻率，Sw为含水饱和度，b为岩性系数，n为饱和度指数。

本文模拟沉积物孔隙中只存在水和THF水合物，因此在计算得到含水饱和度后即可得到含水合物饱和度，即Sh=1-SW。上述公式中参数a﹑b﹑m﹑n的取值会影响水合物饱和度的计算结果，因而确定参数的合理取值是利用阿尔奇公式准确计算水合物饱和度的关键。当沉积物中不含泥质成分时，a值通常取值为1[23]。

在已知模拟沉积物的孔隙度φ的条件下，为了确定胶结指数m的值，需要测量模拟沉积物完全水饱和时的阻抗幅值|Zo|和孔隙水的阻抗幅值|Zw|，并分别代替式(6)中的Ro和Rw，进而计算得到地层因子F，最终求解出m。

图8给出了测试频率范围内胶结指数m的值。考虑到m与储层物性﹑孔隙结构等有关，因此利用图8选择合适的频率范围使得m为一稳定值，即在测试频率200～200 kHz时，m较为稳定，其平均值为1.35。

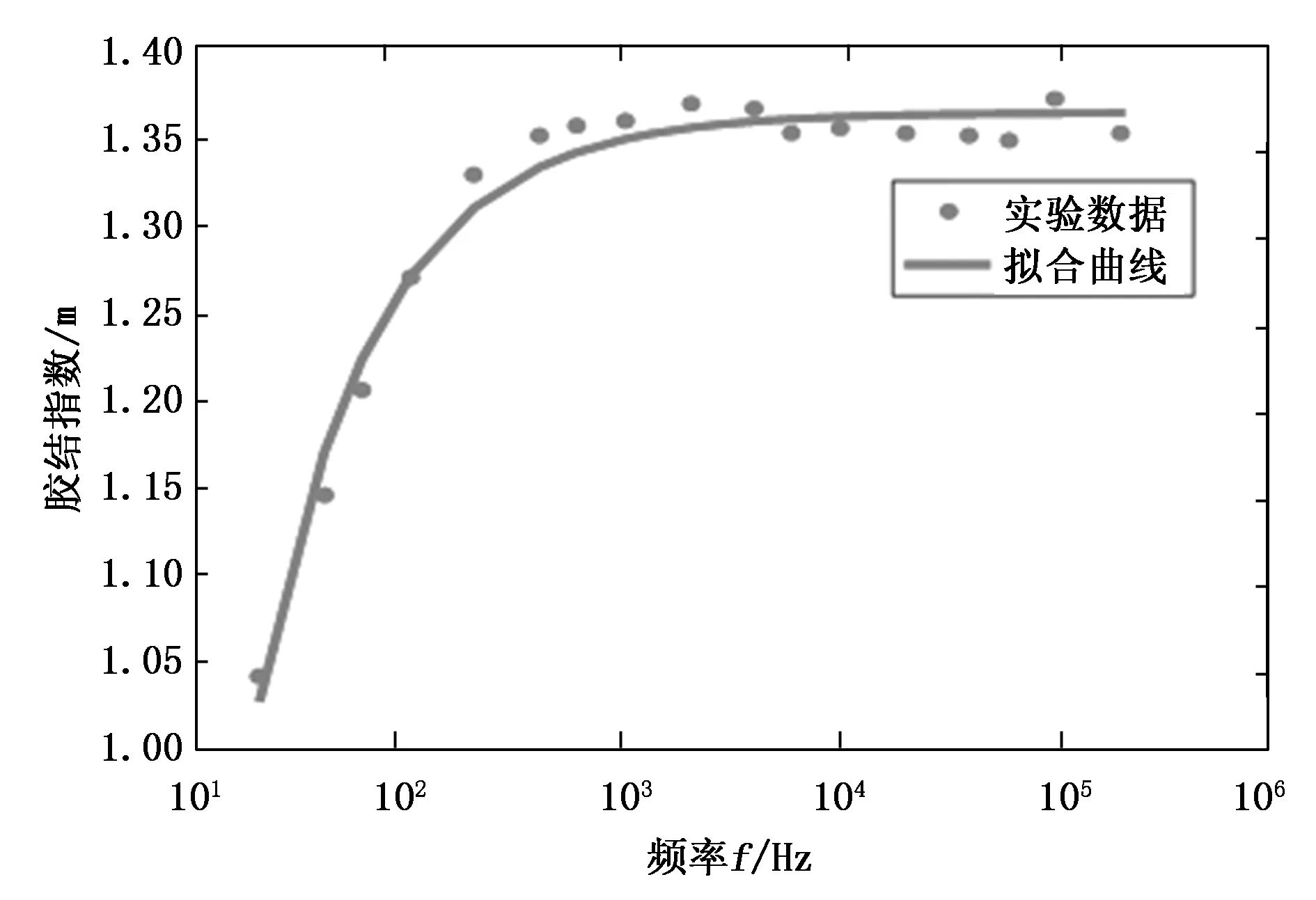
图7 胶结指数m与频率f的关系曲线

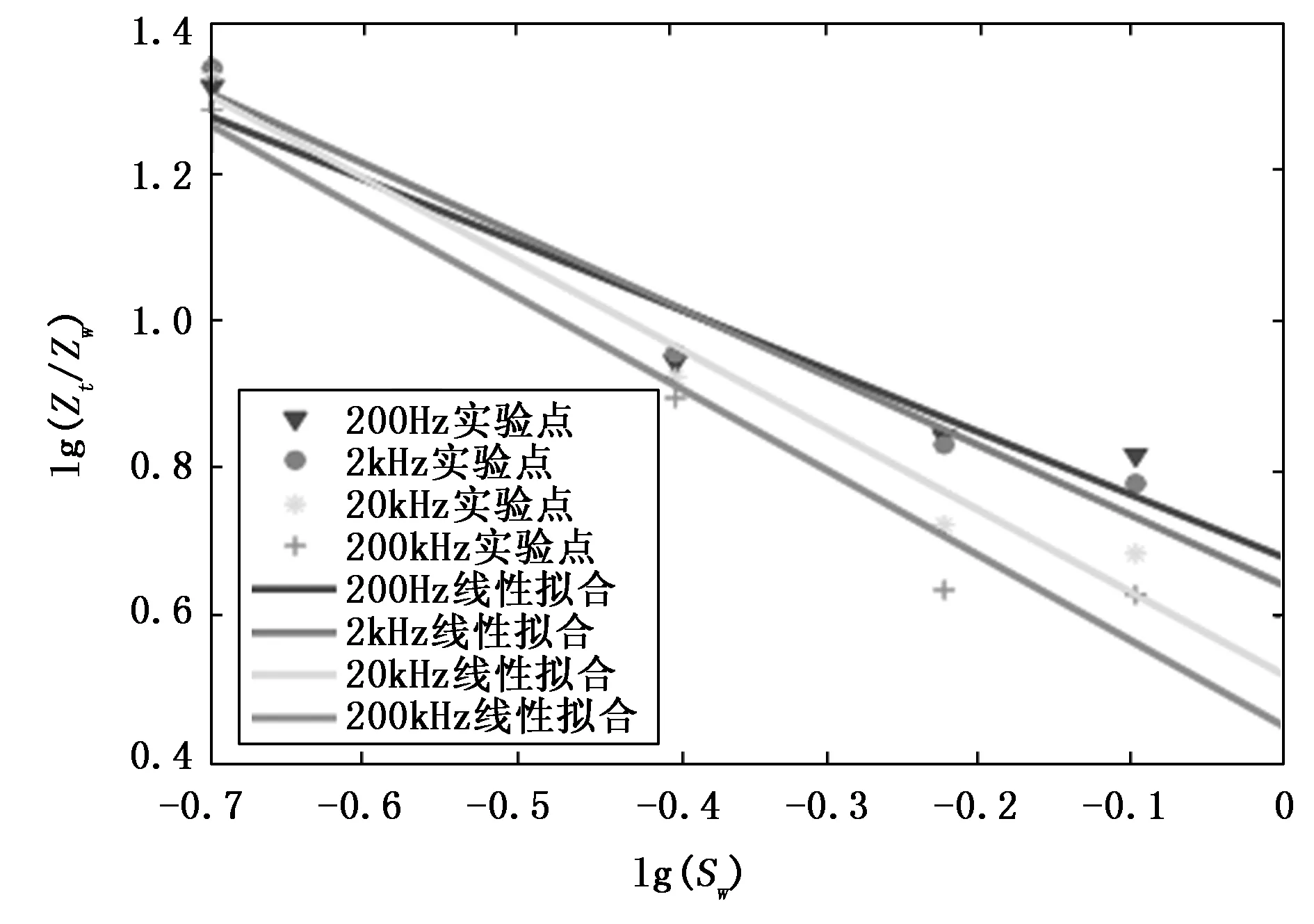
图8 不同测试频率下实验数据的线性拟合

为了求解岩性系数b和饱和度指数n，将式(6)与式(7)联立，并用模拟沉积物阻抗幅值|Zt|代替Rt，得到变形后的阿尔奇公式：

(8)

对式(8)两边同时取对数，并将a=1﹑m=1.35和φ=0.4代入，得到式(9)：

(9)

利用不同测试频率下的实验数据对式(9)进行线性拟合则可得到岩性指数b和饱和度指数n。

由图8可知：不同频率拟合出的直线截距差别不显著，考虑到岩性系数b由多孔介质自身的物理性质所决定，所以将各个截距值取平均作为b的取值，即b=1.13；当测试频率不同时拟合直线的斜率不同，说明饱和度指数n受到频率的影响，因此将n与lg(f)进行线性拟合(如图9所示)，表达式如下：

图9 饱和度指数n与lg(f)的线性拟合

n=0.12lg(f)+0.57

(10)

在确定了阿尔奇公式中4个参数a﹑b﹑m﹑n后，即可得到基于阻抗幅值和频率的含水合物饱和度计算模型：

(11)

式中,f为测试频率，其范围为200 Hz～200 kHz。

4 结束语

以自主设计开发的水合物电学参数测量装置为基础，首先建立了四氢呋喃水合物模拟实验的步骤与宽频电阻抗测试方法，然后在频率范围5 Hz～400 kHz内测试了不同饱和度条件下的含水合物海沙体系的宽频阻抗。基于测试数据分析了水合物生成分解过程中模拟沉积物的宽频阻抗特性、不同含水合物饱和度条件下的阻抗幅值频散特性及其与饱和度之间的定量关系，最后建立了基于宽频阻抗幅值和阿尔奇公式的含水合物饱和度计算模型。通过研究得到以下结论：

1)含水合物天然海沙体系的阻抗幅值呈现出频散特性，在频率5 Hz～400 kHz范围内该频散特性受到孔隙壁与孔隙流体之间界面极化效应的影响，阻抗幅值频散度与含水合物饱和度之间呈现近似线性关系。

2)在测试频率200～200 kHz时，阿尔奇公式中的胶接指数m较为稳定，因此限定了所建立模型的频率应用范围；饱和度指数与测试频率的对数之间呈现出近似线性的关系，因此在含水合物饱和度计算模型中应加入测试频率这一参数。

本文的研究为沉积物中含水合物饱和度的评价提供了新的测试与计算方法，所提出的含水合物饱和度计算模型适用于较宽频率范围的阻抗幅值，从而扩展了阿尔奇公式的应用范围。实际应用中，可同时测量多个测试频率的阻抗幅值并应用所提出的模型对含水合物饱和度进行计算，综合多个计算结果进而获得更加可靠的饱和度评价值。此外，还可将上述模型与声学测试数据/声学模型相联合[24]，建立电声联合模型，如阿尔奇公式与权重方程联合，综合声电测试数据以期获得更加可靠的储层含水合物饱和度评价结果。