非线性间歇过程的迭代学习状态估计

吴宏亮，赵忠盖，刘 飞

(1.轻工过程先进控制教育部重点实验室,江苏 无锡 214122;2.江南大学 物自动化研究所，江苏 无锡 214122)

0 引言

间歇过程是一类重复生产过程，按照相同的工序以批次为单位进行产品生产，越来越多地应用于食品、生物制药以及化工领域。间歇过程中很多关键参数直接与产品质量相关，需要对其进行实时监测。但是，受限于传感器技术的发展，间歇过程中的许多状态变量难以测量或者测量成本很高，因此对间歇过程状态变量的估计尤为重要，一直是工业界和学术界的关注焦点[1]。卡尔曼滤波(Kalman filter,KF)是一种广泛应用的最优状态估计的方法，但它适用于线性系统，而间歇过程通常具有非线性特性。对于非线性系统，通常采用扩展卡尔曼滤波(Extended Kalman filter,EKF)方法，无迹卡尔曼滤波和粒子滤波方法等[2-5]。但是，这些方法往往是连续过程状态估计的简单复制，忽略了批次之间的相关性。

近年来，为了提高间歇过程状态估计的性能，迭代学习策略被引入状态估计，考虑了批次运行之间的重复性和时间方向动态特性。迭代学习的思想来自于重复过程的控制，Arimoto等[6]提出一种迭代学习控制(iterative learning control,ILC)方法，针对重复运行的被控系统，通过前一次或前几次的控制误差信息修正当前操作的控制输入，最终实现在整个时间区间上系统的输出完全跟踪上期望轨迹。基于迭代学习的思想，文献[7-9]设计了确定性重复系统的迭代学习观测器。然而，实际间歇生产存在噪声干扰。

Zhao等[10]考虑包含随机噪声的非线性间歇过程，提出了一种用于批处理的迭代学习状态估计算法，在当前批次粒子滤波的基础上，引入上一批次输出值的估计误差作为修正项，包含了上一批次的信息，但修正项难以确定。Cao[11]等人提出了一种鲁棒迭代学习卡尔曼滤波方法，用于状态和输出矩阵均具有范数有界不确定性的重复过程系统的状态估计，但只给出了一种先验类型估计。在文献[12]中，提出了线性系统的迭代学习卡尔曼滤波器(Iterative learning Kalman filter,ILKF)，并在重复注塑机过程中进行了估计研究，验证了ILKF在间歇过程中优越的估计性能。

但是，文献[12]中的ILKF方法是一种线性状态估计方法，而大多数间歇过程非线性严重。本文将基于标称模型的拟线性化方法引入到间歇过程状态估计中来，提出一种迭代学习拟线性卡尔曼滤波(Iterative learning quasilinear Kalman filter,ILQKF)方法。其中，标称模型是间歇过程含噪声模型的期望[13]，可以根据机理建模求得。考虑间歇过程正常运行下，每个时刻的状态在标称轨迹周边变化，而状态的变化呈现线性特征，因此ILQKF以实际状态与标称状态之间的误差为新状态，首先基于标称轨迹的拟线性化方法建立了与误差相关的线性化模型；然后，应用ILKF方法对误差模型进行状态估计，而状态轨迹等于误差轨迹与标称轨迹之和。ILQKF在状态估计中充分利用了时间和批次双维的特性，并消除了重复误差。此外，相比ILKF方法，ILQKF还具有更宽松的初值条件。ILKF方法需要假设系统的初值满足正态分布且均值为零，这在间歇过程中是一个不合理的假设，比如发酵过程的初始状态可能是一个已知的非零量，如发酵过程中底物的初始浓度和发酵罐中的初值生物质浓度通常是一个给定的值，ILQKF方法更具有实用性。本文通过啤酒发酵例子验证了ILQKF算法优越的性能。

1 迭代学习卡尔曼滤波

ILKF方法结合了KF和ILC的思想，充分利用了间歇过程的多批次重复性。

对于线性间歇过程系统模型(1)：

(1)

其中:k是系统的批次数，k∈[1,+∞)，t是采样时间，t∈[0,M]，xk(t)∈Rn是第k批、第t时刻的状态变量，yk(t)∈Rl是第k批、第t时刻的输出变量，l≤n，d(t)是系统每批的重复干扰，为了设计ILKF，作以下假设[12]：

假设1：ωk(t)和vk(t)分别是独立的双维高斯过程噪声和测量噪声：

E[ωk(t)]=E[vk(t)]=0

E[ωi(j)vkT(t)] = 0

E[wi(j)wkT(t)] =Qδj,t;i,k

E[vi(j)vkT(t)] =Rδj,t;i,k

δj,t;i,k是双维克罗内克函数，仅当j=t,i=k时，δj,t;i,k=I，否则δj,t;i,k=0。

假设2：d(t)为未知的有界重复干扰，随时间变化。

假设3：初始条件xk(0)服从的独立正态分布N(0,ζ)。

以上3个假设中,假设1与假设2相当于间歇生产过程中的两种干扰，而假设3对初值的假设不符合绝大多数情况，本文第2节和第3节将给出合理解决假设3的方法。

定义δ为批次方向的后向差分算子：

δxk(t)=xk(t)-xk-1(t)

δyk(t)=yk(t)-yk-1(t)

(2)

同样可以定义δxk(t),δyk(t),δωk(t),δvk(t)。

可以将系统改写为两个子系统，分别为时间方向上的子系统∑T和批次方向上的子系统∑B：

(3)

(4)

可以发现在∑B中，xk(t)与xk-1(t)之间的转移矩阵是单位阵，即批次子模型∑B是个临界稳定系统，可能会导致xk(t)的值不断上升或震荡，可以在原∑B子系统中加入系数τ<1，使系统稳定[12]：

(5)

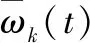
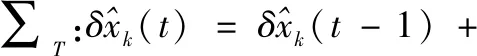
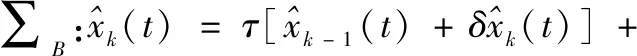
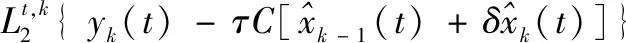
(6)

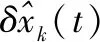
在间歇过程运行时，系统干扰分为重复干扰d(t)，随机噪声ωk(t)和vk(t)。通过把系统分解成时间方向和批次方向的子系统，并且设计子系统相应的估计器，抑制了随机噪声和重复干扰，并提高了间歇过程的估计精度。

图1是ILKF双向动态特性图，其中横轴Time代表时间方向，纵轴Batch代表批次方向，箭头表示传递方向，此外在每个采样时刻都有对应的测量值。横轴上x的转移只是随着时间转移，纵轴的x则通过批次方向的卡尔曼滤波进行更新，并且引入了矫正项δx，这个矫正项也可称为学习项，它在时间方向上通过卡尔曼滤波进行更新。

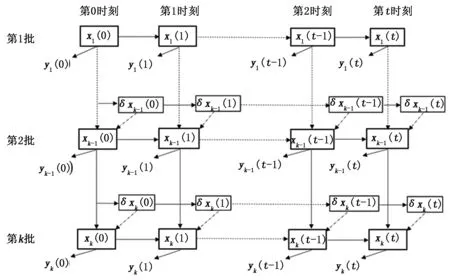
图1 ILKF双向动态特性图

2 非线性系统的拟线性化

2.1 动机

针对文献[12]中的ILKF存在的非线性问题和不合理的初值假设等，本文将通过基于标称轨迹的拟线性化方法将ILKF推广到非线性间歇过程，并构造了一个误差系统，通过对误差系统的状态估计来获得系统的状态估计，可以放宽初始值的假设。

考虑非线性间歇过程系统模型(7)：

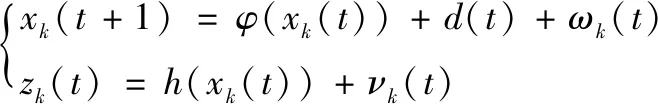
(7)

第1节中针对干扰的合理假设1和假设2在本节仍然成立；针对假设3，本节系统初值可以分布在任意均值的高斯分布中。

2.2 基于标称轨迹的拟线性化方法

基于标称轨迹的拟线性化方法对非线性模型(7)进行了线性化处理，在本节中，引入了一个误差状态系统，误差系统的状态为原系统状态轨迹和标称轨迹的偏差，通过估计误差系统的状态来得到非线性系统的状态估计。由于存在干扰和噪声，每批次运行所产生的状态轨迹是不同的，但均是在标称轨迹附近的波动[13]。

假设4：实际轨迹接近于标称轨迹。

(8)

并且定义Δ为状态的真实轨迹和标称轨迹的误差算子：

(9)

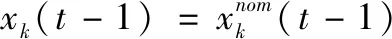
xk(t)=φ(xk(t-1))+d(t-1)+ωk(t-1)=

(10)

基于假设4，由(9)和(10)可得：

△xk(t)=Φ(t-1)△xk(t-1)+d(t-1)+ωk(t-1)

其中一阶偏导近似系数为：

(11)

同理可得：

△zk(t)=Hk(t)△xk(t)+vk(t)

(12)

其中一阶偏导近似系数Hk(t)为：

(13)

可以得到新的线性化系统：

(14)

Φ(t-1)和H(t)分别如式(11)和式(13)所示。

2.3 时间和批次方向的子系统

由式(2)中δ的定义易知：

δ△xk(t)=△xk(t)-△xk-1(t)

δ△zk(t)=△zk(t)-△zk-1(t)

工业生产中重复非线性过程一般每一批都是从相同的初始值开始，根据机理或者经验模型，每一批都具有相同的标称轨迹：

(15)

则根据式(2)和式(9)可得：

δxk(t)=xk(t)-xk-1(t)=△xk(t)-△xk-1(t)

即δxk(t)=δ△xk(t)，结合式(14)有递推式：

δ△xk(t)=△xk(t)-△xk-1(t)=

Φ(t-1)δ△xk(t)+δωk(t-1)

同理：

δ△zk(t)=△zk(t)-△zk-1(t)=

H(t)δ△xk(t)+δvk(t)

参考式(3)～(4)将式(14)改写成时间和批次两个子系统，时间方向上的子系统∑T：

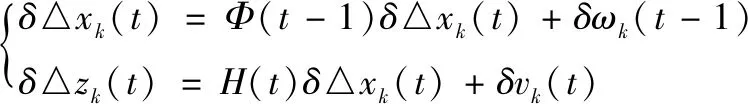
(16)

批次方向上的子系统∑B：

(17)

(18)

2.4 相关量的计算

本小节计算迭代学习卡尔曼滤波中需要用的量，相关噪声协方差计算如下：

E[δωk(t)δωkT(t)] =

E[(ωk(t)-ωk-1(t))(ωk(t)-ωk-1(t))T] =

E[ωk(t)ωkT(t)] +E[ωk-1(t)ωkT(t)]=2Q

E[(ωk(t)-ωk-1(t))(ωk-1(t)-ωk-2(t))T]=

所以有：

定义:

由式(14)得：

(19)

(20)

3 迭代学习拟线性化卡尔曼滤波

本节针对非线性间歇过程的状态估计问题，基于ILKF方法引入标称轨迹拟线性化方法，提出了一种迭代学习拟线性化卡尔曼滤波(ILQKF)方法。ILQKF与已有的传统状态估计方法相比有以下三点的改进。

首先，与现有的非线性滤波方法比，现有的非线性滤波方法只考虑了时间方向的状态转移，而ILQKF参考ILKF的滤波框架可以利用之前所有批次的状态信息，使得状态估计误差可以随时间和批次两个方向减小。

其次，与ILKF方法比，ILKF只针对线性系统，很难运用到非线性间歇生产过程上，而ILQKF引入拟线性化方法可以解决非线性问题，更适合运用到实际生产过程。

最后，与ILKF方法比，有着更为宽松的初始条件，在ILKF中，由于中间量的计算需要，文献[12]给出了假设3，即原系统的状态初值满足0均值的正态分布。事实上，如果不满足假设3，ILKF的递推式将会变得极复杂，并且不为0的初值可能会使得批次子系统中的误差协方差变大，从而降低滤波器的性能。然而，ILQKF不必满足假设3，其依据在于拟线性化时引入了标称模型作为中间变量。当系统初值满足任意高斯分布，将高斯分布的均值作为标称轨迹初值，则新状态仍是0均值的正态分布，即ILQKF可以用于初值期望不为0的非线性系统的状态估计。

3.1 ILQKF估计结构

与ILKF类似，基于ILQKF设计状态估计器分为两个阶段：时间方向状态估计和批次方向状态估计。时间方向状态估计包括对时间子系统ΣT的时间更新和测量更新；批次方向状态估计包括对批次子系统ΣB的批次更新和测量更新。ILQKF的双向动态特性与图1不同点在于系统估计对象不是原系统状态xk(t)，而是状态与标称轨迹的误差Δxk(t)。

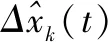
时间子系统ΣT的状态估计器如下：

(21)

批次子系统∑B的状态估计器如下：

(22)

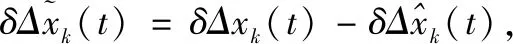
基于式(16)与式(21)得到∑T的估计误差系统为：

(23)

基于式(18)与式(22)得到∑B的估计误差系统为：

(24)

定义下列误差协方差矩阵：

3.2 时间方向状态估计

1)子系统∑T的时间更新：

(25)

(26)

2)子系统∑T的测量更新：

(27)

(28)

(29)

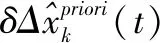
3.3 批次方向状态估计

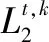
通过式(18)、式(22)，可得计算批次系统的估计误差协方差Ck：

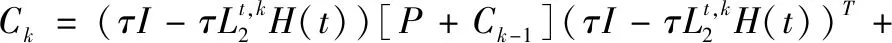
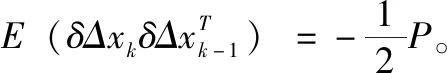
根据式(23)，式(24)和性质1，我们可以计算得到下面这些相关协方差：

批次方向状态估计流程：

1)子系统∑B的批次更新：

(30)

(31)

(32)

2)子系统∑B的测量更新：

(33)

(34)

(35)

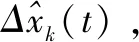
(36)

下面给出ILQKF算法：

算法开始：

输入：φ(xk(t-1)),h(xk(t)),Q,R,zk(t),M,K；

循环开始，t=1：

当t=M，循环结束，否则t=t+1。

滤波开始，k=1：

循环开始，t=1：

当t=M，循环结束，否则t=t+1；

当k=K，滤波结束，否则k=k+1；

算法结束。

4 啤酒发酵过程仿真

啤酒发酵过程是一种输入为生物质(酵母)，基质(糖)和水，输出为酒精，二氧化碳和水的间歇反应过程。发酵过程中，糖类和酵母的浓度都必须控制在合理的范围之内[15]，因此十分有必要对啤酒发酵过程中的糖浓度和酵母浓度进行状态估计。

将所提出的ILQKF方法应用到啤酒发酵过程的步骤如下：

步骤1：根据已有数据或者机理确定啤酒发酵的非线性标称模型。

步骤2：初始批生产开始时，用EKF算法对糖浓度与酵母浓度进行估计。

步骤3：从第二批生产开始，以上一批的估计数据和标称模型为基础，用ILQKF算法进行估计，直到生产结束。

啤酒发酵过程中的糖浓度和酵母浓度的状态空间模型[16]如下所示：

d(t-1)+ωSk(t-1)

Xk(t-1)+d(t-1)+ωXk(t-1)

zSk(t)=Sk(t)+vSk(t)

zXk(t)=Xk(t)+vXk(t)

其中:Sk(t)，Xk(t)，zSk(t)，zXk(t)，ωk(t)，vk(t)分别代表第k批次、第t时刻糖浓度，酵母菌丝的浓度，糖浓度的测量值，酵母菌浓度的测量值，过程噪声，测量噪声，ωk(t)和vk(t)相互独立。d(t)表示每批只随时间变化的重复性干扰，tc表示采样间隔。模型参数如表1所示。

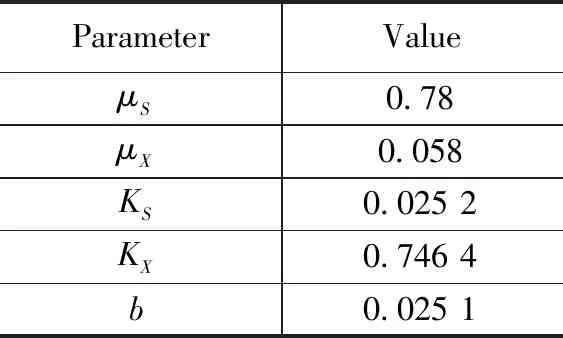
表1 模型参数表

设定步长为[0,3000]，初始值x(0)=xnom(0)=[S(0),X(0)]=[30;3]，白噪声协方差矩阵Q=[0.00001,0;0,0.00001]，R=[0.25,0;0,0.0025]，设置τ=0.96，σ=10-12。

仿真时，初始批，即k=0批时，直接采用EKF进行状态估计；从k=1批开始，将第0批由EKF得到的状态估计值与标称状态之差作为ILQKF第1批的初始估计值，再采用ILQKF算法得到之后每一批的状态估计值。

图2显示了啤酒发酵中基质(糖)和生物质(酵母)的状态估计结果图，实线代表实际值，虚线代表估计值。计算第20批基质浓度和生物质浓度平均估计误差分别为0.082 203与0.017 091；计算第100批基质浓度和生物质浓度平均估计误差分别为0.014 453与0.01 033。可以发现估计精度随批次增加而增加。这是由于ILQKF建立了批次间的传递关系，可以过滤批次间的重复干扰，随着批次的增加，滤波使用的信息越来越多，估计效果也越来越好。

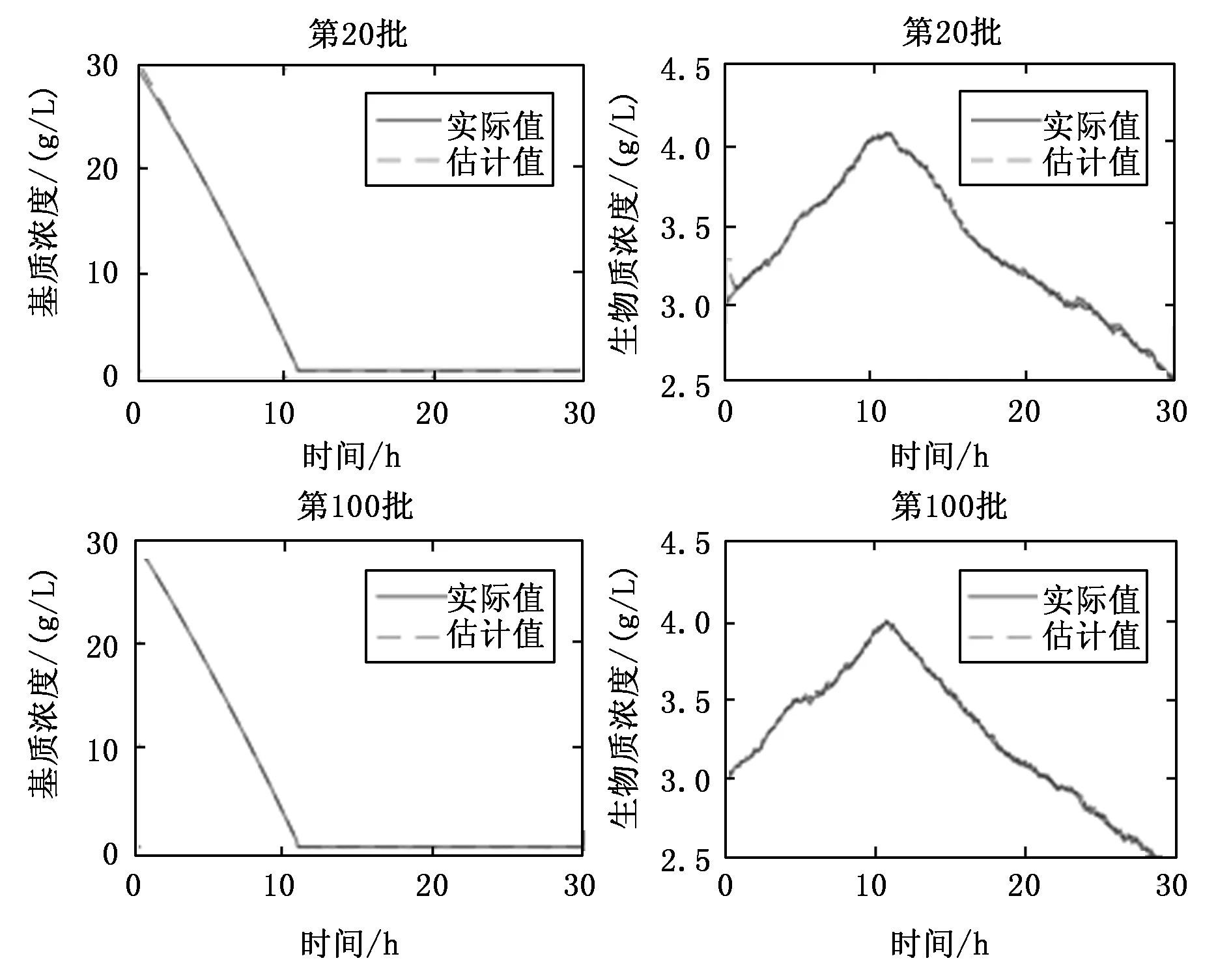
图2 啤酒发酵状态估计结果

图3比较了EKF和ILQKF的状态估计误差。由于EKF估计对于每一批次都是独立的，估计精度只依赖于初始值与动态噪声的大小，随着批次的增加，EKF的估计误差没有很大变化。而ILQKF可以利用上一批次的估计信息更新初始值减小初始误差，还同时考虑了重复干扰与动态噪声，随着批次的增加，ILQKF状态估计误差逐渐收敛。图3结果也表明ILQKF估计误差随批次递减，而EKF估计误差随批次变化不大，所以ILQKF在多批次运行时的状态估计效果明显优于EKF。

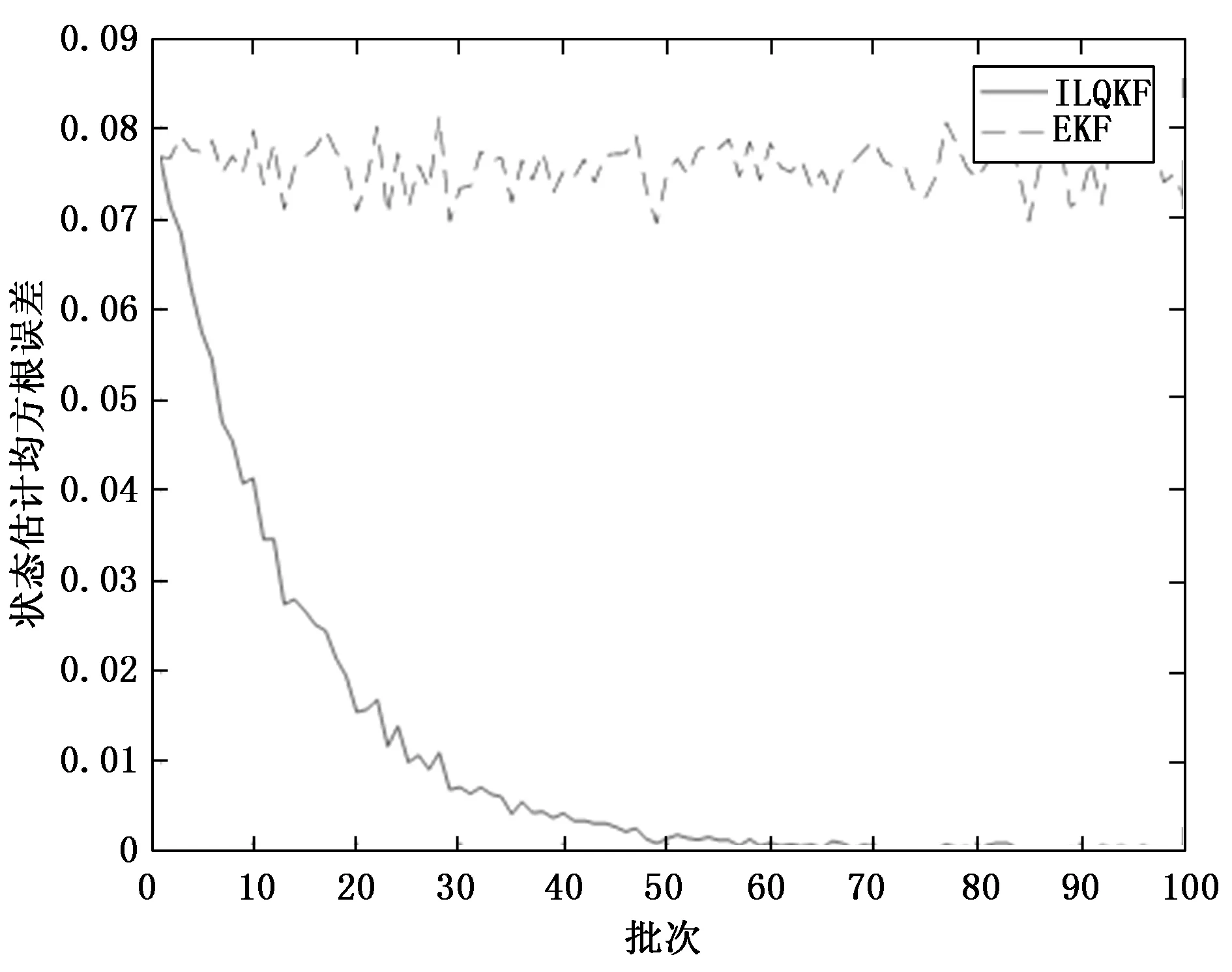
图3 ILQKF和EKF的状态估计误差对比

5 结束语

本文基于迭代学习和标称轨迹线性化的思想，设计了一种用于间歇过程的迭代学习拟线性化卡尔曼滤波器。该ILQKF方法将文献[12]的ILKF方法扩展到非线性过程中，利用了间歇过程多个批次的信息，设计了时间方向和批次方向相应的卡尔曼滤波器，得到当前批次当前时刻的状态估计值。啤酒发酵过程的仿真结果表明，状态估计误差随批次的增加而减小直至收敛，相对于传统的估计方法有一定的优势。