基于变结构控制的固定前置角制导律设计
2020-09-02马清华苗昊春闫智强
马清华,成 高,苗昊春,闫智强,马 骏
(西安现代控制技术研究所,西安 710065)
0 引言
合成孔径雷达(SAR)是一种主动式现代高分辨力微波遥感成像雷达[1]。近年来,得益于数字信号压缩处理技术、微波成像技术、微电子技术、天线技术及数字计算机领域的迅猛发展,合成孔径技术得到了进一步的发展与完善[2-3]。军事上,为了获取高分辨率的景象匹配图象以及目标区域地貌特征等,合成孔径雷达的研究也越来越受到重视[4-8]。另一方面,精确制导武器作为现代战争中举足轻重的角色,其精确打击的关键在于导引头对目标的识别、分辨和捕获的能力。相较于红外成像导引头、可见光成像导引头、激光雷达导引头等,合成孔径雷达导引头具有明显的优势[9]。其通过对导弹飞行过程中不同弹目关系下回波阵列信号的接收和处理,提高方位分辨能力。具有全天时、全天候的工作能力,不会受限于地形、地貌、恶劣的天气条件以及战场上的火光、烟雾干扰等影响,并且具有一定的穿透能力,可以识别伪装、遮蔽物后方的目标[10-16]。
合成孔径雷达(SAR)具有的种种优势为现代战争中精确制导武器的发展方向提供了一种新的思路。然而,弹载合成孔径雷达(合成孔径雷达导引头)在应用时仍受到一些限制,其末制导段采用的前侧视工作模态与弹目相对运动关系、弹体姿态等密切相关[17-18],因而,为了确保SARS采用前侧视工作模态下,其具有良好的成像效果和工作性能,必需保证前侧视条件成立,因而必需设计固定前置角制导律,规划合理弹道方案。
1 系统模型的建立
弹目相对关系如图1所示,由图可得弹目相对运动方程[4]如下:
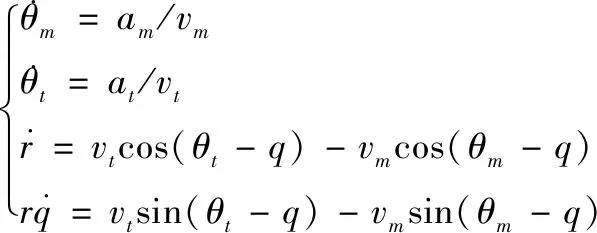
(1)
所谓速度前置角,是指导弹在飞行过程中某一时刻,导弹速度方向超前弹目连线(视线)方向的夹角。式中,r为弹目之间的距离;vm,vt分别表示导弹运动速度和目标运动速度;am,at分别表示导弹法向加速度和目标法向加速度;q为基准线下的视线角;θm,θt分别为导弹和目标的速度方向角(速度矢量和基准线之间的夹角);ηm,ηt分别为导弹和目标的速度矢量和视线之间的夹角,即速度矢量前置角。
弹目相对运动关系建立后,需要建立系统的误差模型。
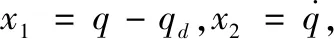

(2)
式中,
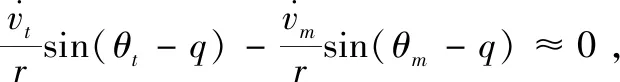
(3)
2 变结构固定前置角制导律设计
基于式(2)设计变结构制导律[5]。
选取滑模面为:
(4)

(5)
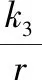
下面基于选取的滑模切换函数和趋近律,推导固定前置角制导律。
对式(4)两边求导得:
(6)
注意到期望视线角存在以下关系式:
(7)
然后将式(1)、(5)和(7)代入式(6),可得:
(8)
合并同类项后得:
(9)
进而可得指令加速度为:
(10)
由于
(11)
将式(3)和式(11)代入式(10)后,制导律式(10)可以改写成如下形式:
(12)
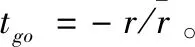
另外,该导引律中含有关于目标加速度的补偿项,当打击目标为机动目标时,需要通过雷达获取目标加速度信息。
由于实际系统中存在各种测量误差和随机干扰,因而在确定各项增益系数时应充分考虑参数适应性及波动范围,避免由于干扰或随机误差等系统因素影响控制品质。
3 固定前置角导引法性能分析
下面从理论上对固定前置角制导律的弹道特性进行分析。
为了得到固定前置角导引的一般特性,作如下假设:目标作等速直线运动,导弹作等速运动。
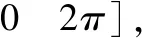
1)情形1:考虑当导弹的弹道倾角大于视线角一个小角度Δq时:
弹目相对运动关系如图2所示,视线角的变化率可采用如下方程表示:

图2 当弹道倾角始终大于视线角一个小角度Δq时,弹目相对运动图
(13)
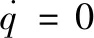
或
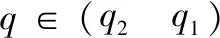


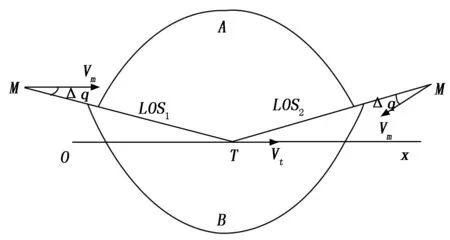
图3 当弹道倾角始终大于视线角一个小角度Δq时,视线角变化趋势图
如果视线落在A区域内,则视线将会沿着逆时针方向转动,趋向于LOS1;当视线落在B区域内,则视线将会沿着顺时针方向转动,趋向于LOS1;当视线与LOS1或LOS2重合时,拦截弹将沿直线攻击目标。
2)情形2:考虑当导弹的弹道倾角小于视线角一个小角度Δq时:
弹目相对运动关系如图4所示,视线角的变化率可采用如下方程表示:
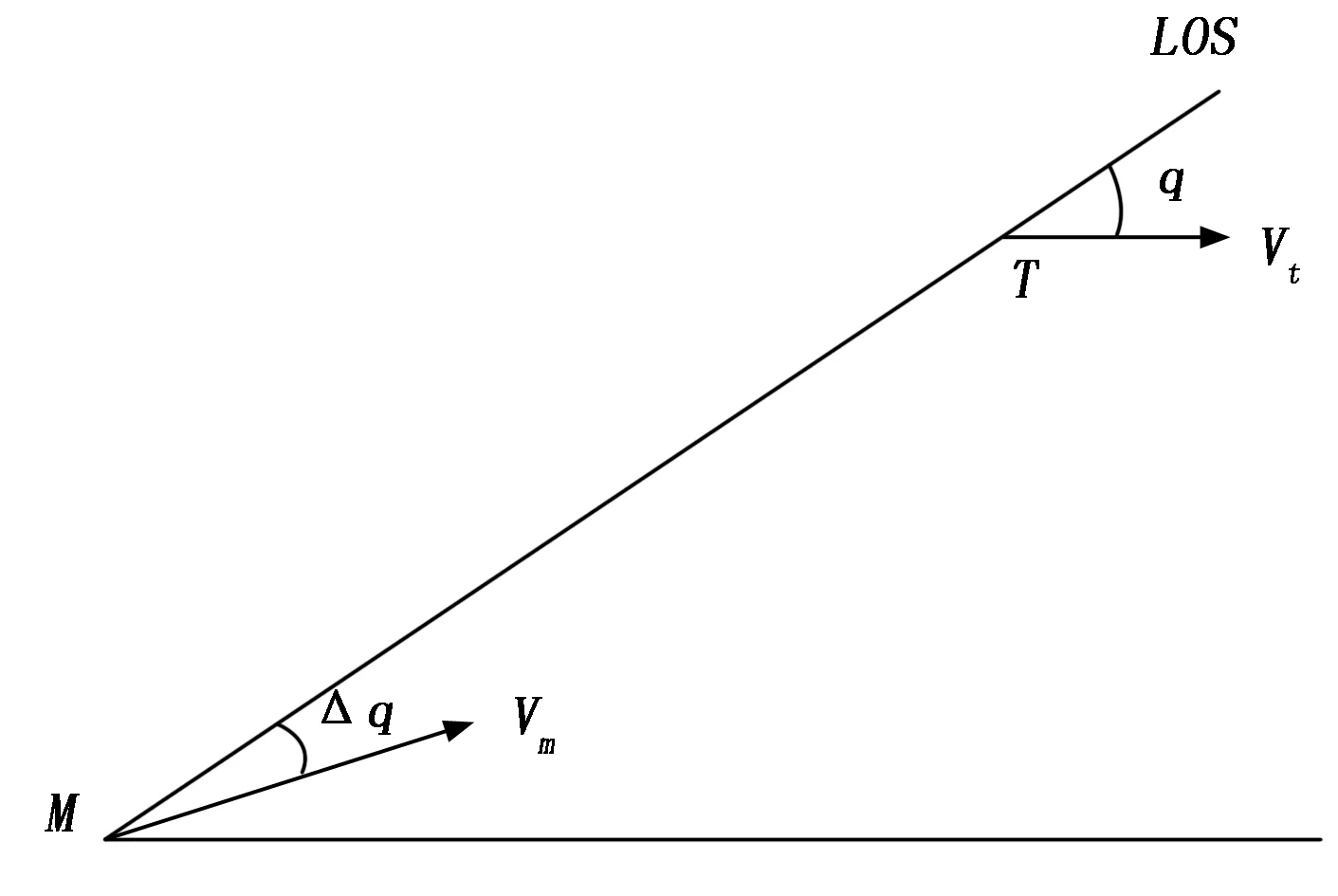
图4 当弹道倾角始终小于视线角一个小角度Δq时,弹目相对运动图
(14)
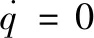
或
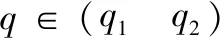
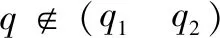
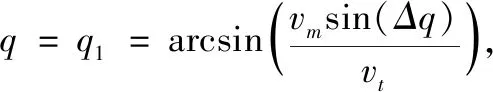
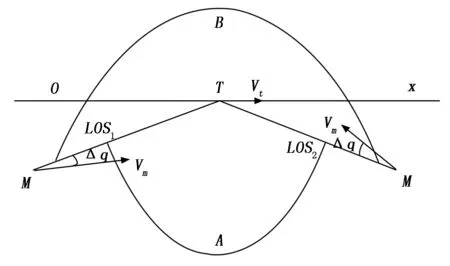
图5 当弹道倾角始终大于视线角一个小角度Δq时,视线角变化趋势图
如果视线落在A区域内,则视线将会沿着顺时针方向转动,趋向于LOS1;当视线落在B区域内,则视线将会沿着逆时针方向转动,趋向于LOS2;当视线与LOS1或LOS2重合时,拦截弹将沿直线攻击目标。
根据上述分析可知,固定前置角导引法具有如下特点:
1)能够约束导弹拦截轨迹跟踪指定的固定前置角,从导引律角度上约束了导引头与目标的视线方向,以保证合成孔径雷达前侧视成像条件成立;
2)由于需要跟踪一个固定的前置角,因此导弹有绕到目标的侧后方去追击目标的攻击趋势,这样会导致拦截弹道较为弯曲(尤其是在命中点附近);
3)由于导弹总会绕到目标侧后方攻击,因而在命中点附近需要的法相过载相对较大,从而对导弹的机动性和过载能力提出了一定要求;
4)该导引法在尾追攻击时需要的过载相对于迎击时需要的过载较小;
5)由于导弹有从侧后方尾追目标的趋势,因此需要导弹的速度大于目标的速度,才可能拦截到目标。
4 全空域弹道仿真
在理论分析的基础上,通过数学仿真的方式对固定前置角制导律的攻击特性进行验证。采用等速运动目标0~360°全空域覆盖仿真。
仿真时初始参数:θm=10°,r=10 000 m,q=30°,vm=800 m/s,xm=0,ym=0,xt=8 660.3,yt=5 000;制导律参数为:k1=15,k2=3,k3=0;期望视线角:qd=θm-17.2°;目标匀速直线运动且vt=400 m/s,制导律采用由式(12)表示的变结构固定前置角制导律。当目标的速度方向取不同的数值时,拦截弹道如图6~9所示(参照AIM-9X具体型号指标,导弹过载限制为50 g)。

图6 目标运动方向在0°~90°之间变化时的拦截弹道汇总
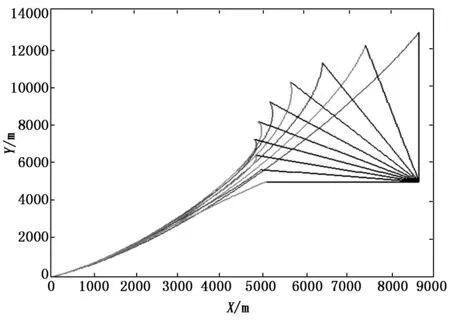
图7 目标运动方向在90°~180°之间变化时的拦截弹道汇总

图8 目标运动方向在180°~270°之间变化时的拦截弹道汇总

图9 目标运动方向在270°~360°之间变化时的拦截弹道汇总
可见,导弹可以实现全向攻击,并且能够保证很小的脱靶量(数学仿真下,全向脱靶量均小于3 m)。其中,导弹攻击侧向运动目标时,脱靶量小于1 m;尾追目标时,脱靶量小于1.6 m。侧向攻击及尾追效果明显要优于迎头攻击,这是因为视线角固定前置角的限制对于导弹有一个持续拉偏的作用,从而使得拦截过程中导弹始终有绕到目标侧后方进行攻击的趋势,由于弹道末端弹目相对运动变化较快,这种趋势在弹道末端表现得尤为明显。这也导致了该固定前置角导引律在拦截弹道末端需要较大的过载,对导弹机动能力提出了较高的要求。
需要指出的是,为了使拦截弹道更加直观地体现出固定前置角制导律攻击特性,在仿真时选取的固定前置角为Δq=17.2°,可以想象,偏置值的增大将会导致控制力增大,从而所需过载也随之增大,弹道则相对更加弯曲。而在实际工程实践中,固定前置角的取值往往很小就能够保证合成孔径雷达导引头的前侧视条件成立,弹道的弯曲程度远小于图中仿真曲线。
5 角度跟踪仿真
固定前置角制导律设计的根本目的在于确保合成孔径雷达导引头前侧视条件成立,因此,视线角跟踪的效果将是衡量该制导律性能的一项重要指标。本节仿真主要用于测试变结构固定前置角制导律能否对期望的视线角进行有效地跟踪。
选取仿真时初始参数:θm=60°,θt=-68°,r=10 000 m,q=60°,vm=400 m/s,xm=5 000,ym=0,xt=0,yt=8 660.3;制导律参数为:k1=15,k2=3,k3=0;目标匀速直线运动且vt=200 m/s,制导律采用由式(12)表示的变结构固定前置角制导律。
1)选取固定前置角Δq=15°,则期望视线角:qd=θm-15°,仿真结果如图10所示。
其中,左图为视线角跟踪期望值效果曲线,右图为拦截弹道,脱靶量为0.49 m。
2)当固定前置角Δq=10°时,期望视线角:qd=θm-10°,仿真结果如图11所示。
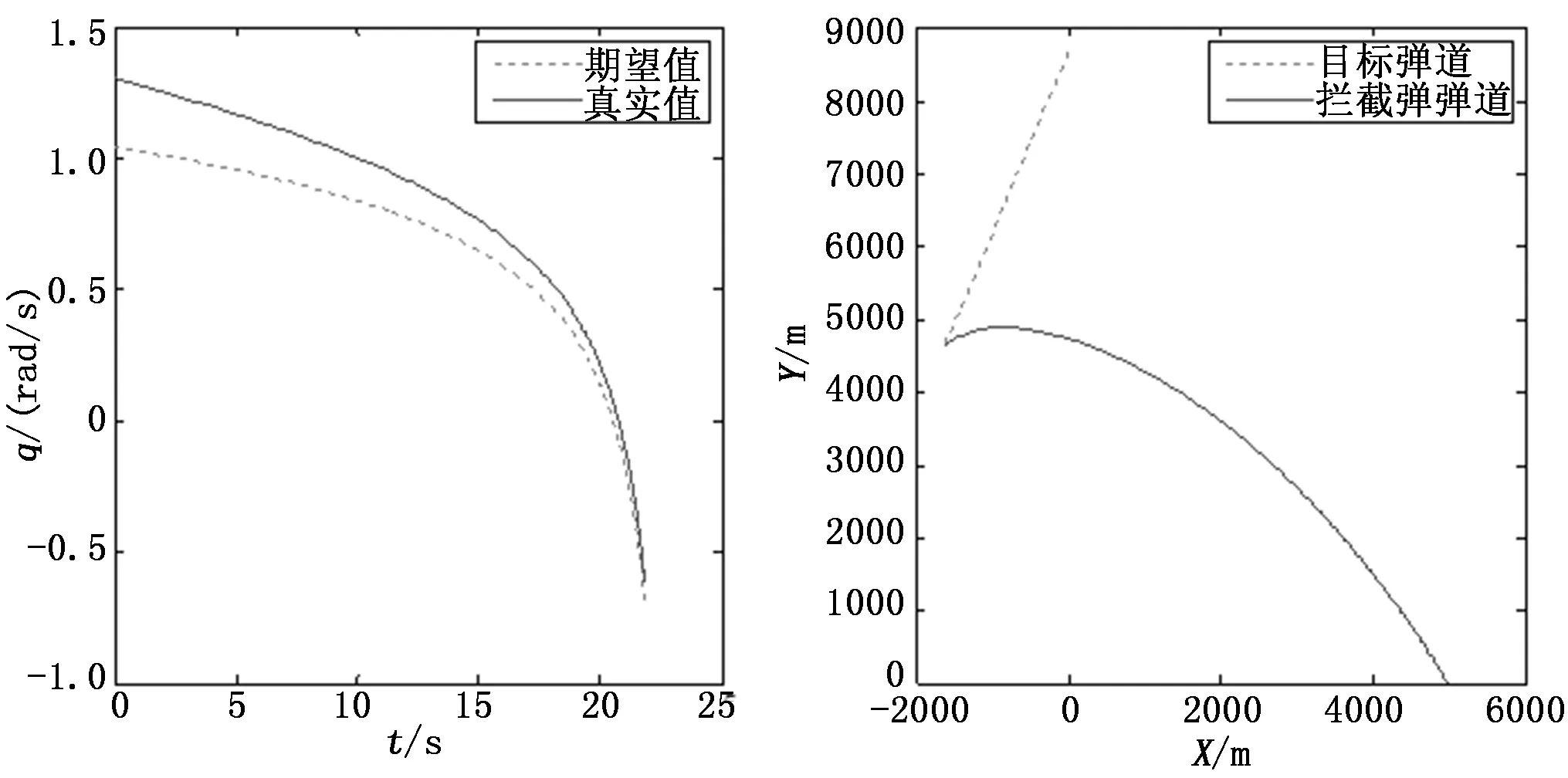
图11 固定偏置10°时仿真结果图
脱靶量为0.32 m。
3)当固定前置角Δq=5°时,期望视线角:qd=θm-5°,仿真结果如图12所示。
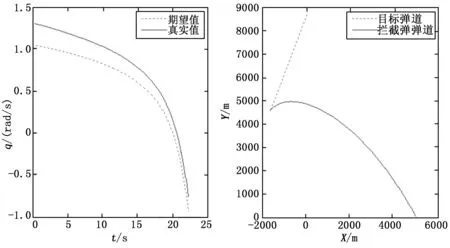
图12 固定偏置5°时仿真结果图
脱靶量为0.21 m。
可见,所选的固定前置角为5°、10°、15°时,视线角真实值总能跟上期望值,且在跟踪过程中真实值总是大于期望值,这说明在导引头跟踪目标过程中离轴角始终大于等于我们所选取的固定前置角。而跟踪收敛的快慢则取决于弹目相对位置初始时刻视线角真实值与期望值之间误差角度的大小。导弹的视线角速率及过载变化曲线如图13所示。
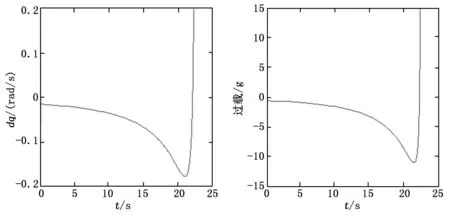
图13 视线角速率及过载(前置角15°)
可见,在拦截末端表征弹目相对运动变化率的视线角速率增大,需用过载也相应增加(11.2 g),这与第三节中固定前置角导引法性能分析的结论一致。
6 结束语
本文针对合成孔径雷达末制导成像角度问题,采用变结构控制方法设计了固定前置角制导律,并进行了仿真验证。得到以下几点结论:
1)使用变结构固定前置角制导律可以实现导弹全空域全向攻击,并且能够保证很小的脱靶量。
2)变结构固定前置角制导律下,视线角真实值跟随期望值效果良好。在制导律参数确定的条件下,跟踪收敛的速率取决于弹目相对位置初始时刻视线角真实值与期望值之间误差角度的大小。
3)通过合理的选择制导律参数,可以调整弹体响应速度,稳定的跟踪指令。
4)通过选择适当的固定前置角,可以调整导弹末制导段弹目关系,以适应合成孔径雷达前侧视成像条件中侧视角度的要求。
