CAN总线中改进的EDF调度算法可调度性分析
2020-09-02张凤登
王 浩,张凤登
(上海理工大学 光电信息与计算机工程学院,上海 200082)
0 引言
CAN总线采用面向消息的优先级控制方式,用标识符定义静态消息优先级,以及其短帧格式和CSMA/CA访问控制,使得CAN具有极高的可靠性和独特的设计,特别适合工业过程控制设备的互连[1],因此CAN总线不仅仅局限适用于车体的控制系统中,在舰艇、航天、检测等控制领域,CAN总线的身影也逐渐增多。从而,国内外的学者均投入了大量精力,针对于CAN总线的调度做研究。最初,由Tindell等人将针对于单处理器的调度分析演化为求消息的最坏响应时间来对CAN总线调度进行分析[2];K.M.Zuberi和K.G.Shin首次提出将EDF算法应用于CAN总线[3],但当时他们提出的方法对CAN做出一些不切实际的假设并且由于时间范围较短,调度能力的体现有一定的局限性,因而Livani对Zuberi等人的方法进行改进[4];国内对于这方面的研究起步较晚,主要集中于理论研究,例如,谌介人、彭军等人提出了基于指数分区的EDF算法,一定程度上较平均分区的EDF算法保证了实时性[5];袁暋、檀明等人针对抢占式和非抢占式的EDF调度算法,提出了任务集新的可调度性测试条件[6]。但是,在某些特殊情况下,现有的EDF算法经常会导致CAN总线无法正常通讯调度,因此针对此现象,本文通过优化算法改善总线仲裁机制完成对消息集的调度,提出了一种新的基于双幂函数分区的EDF调度算法。
1 平均分区EDF算法
1.1 平均分区的EDF算法
EDF(Earliest deadline first)算法是按照绝对截止时间的远近来分配优先级,即消息的绝对截止时间越近,任务的优先级越高。在这种调度机制下,消息的优先级并不是固定的,而是在每次仲裁前依据截止时间的变化,计算相应的动态优先级,最大程度的保证消息不错过其截止时间。EDF算法的核心就是将消息的截止时间通过编码方式转换为标识符的一部分,通过比较标识符大小判定消息的优先级。但是从实际情况可以看出,随着时间的增大,消息的绝对截止时间也会无限增大,当增大到一定程度时,由于标识符位数的限制,从而无法对其编码转为标识符的一部分。针对于此,文献[4]中提出相对截止期的概念,因为消息的时间参考点是每一次仲裁开始时间,所以相对截止时间等于绝对截止时间减去仲裁开始时间,定义:
D=d-ts
(1)
式中,D为相对截止时间。随着ts的增加,D会逐渐减小。根据EDF算法,相对截止时间D会逐渐减小,从而在前一次仲裁失败的消息其D的减小意味着下次仲裁时优先级的提升。当然,即使通过这种优化,相对截止时间表示的时间范围仍会很大,因此Livani提出了平均分区的EDF调度算法。对于一组消息{m1,m2,…,mn},其中,相对截止时间为{D1,D2,…,Dmax},并且按照从小到大顺序排列。平均分区就是将时间轴等分成k段,最后一段区间需要包含最大的相对截止时间Dmax,一般可以直接将时间轴的最大值设为最大相对截止时间,其中每段的时间长度称为基本时间单元U。如图1所示,在每一轮仲裁开始时,根据公式(1)计算出相对截止时间,再根据图1所划分的区域判断相对截止时间在哪个时间段中,再根据当前时间段的区间号来表示消息的优先级。

图1 平均分区示意图
1.2 量化误差的分析和影响
由C.L.Liu[7]等人提出的EDF调度算法判定定理:假定存在一个由n个周期性消息构成的任务集{M1,M2,…,Mn},如果消息i满足如下判定式(2),则该消息可调度。
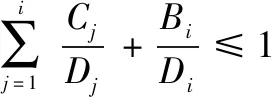
(2)
若任务集中所有消息均满足上式,则该任务集可调度。
其中:Ci为消息i的传输时间,Di为消息i的截止时间,Bi为消息i的最大阻塞时间。
我们通过计算可以得到相对截止时间,尽管这些值可能在数值上的确有些差异,但是在将相对截止时间进行分区时,分割所得到的每个区间是有长度的,无法保障不同的截止时间落到不同的区间中,从而导致不同相对截止时间的消息得到相同的优先级。这是“分区”方案所带来的误差,且无法避免,将这种误差称之为“量化误差”。由图(1)可得,最糟糕的情况下,即两个相对截止时间分别无限接近于某个区间的上下限,此时量化误差最大可近似等于基本时间单元U。因此,在量化误差的影响下,判定式可更新为下式:
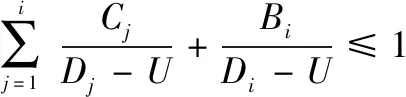
(3)
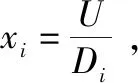
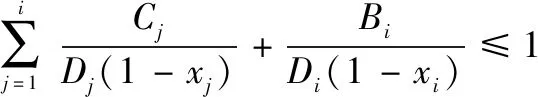
(4)
取max{xi}=x,则:
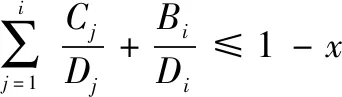
(5)
对比式(2)、(5)可以看出,量化误差对CAN总线的消息传输带来影响,且使得任务可被调度的条件更为严苛。
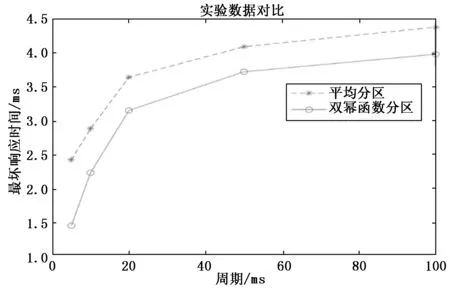
若存在消息mi和mj的标识符分别为Ii和Ij且Ii>Ij,即mj的优先级高于mi。参考图1,当两个消息的相对截止时间十分接近时,且Di 由于平均分区的缺陷,使得优先级反转现象频出,也正是基于此,本论文提出新的幂函数分区方法。 具体过程如下:采用以a为幂指数的方式对相对截止时间Dmax进行分区,a的值取决于实际的系统情况。为简化计算,以及考虑到CAN总线通讯时各节点处理器的工作情况,第二次使用幂函数分区时,幂指数取1。幂函数分区使得不同截止期的消息更容易分到不同的母区间内,更好地保证了消息的实时性。分区方法如图2所示。 图2 双幂函数分区示意图 Ui,j= (6) 令右式记为函数f(x),利用数学方式求极限[8]: 所以如果已有: 则必有: (7) (8) 显然,满足判定式(8)时,任务集是可被调度的,各参数的取值取决于实际环境中消息截止期的分布范围,选取合适的参数值可以获得合适的分区范围,从而使得调度性能得到优化。通过对比图1和图2可以发现,采用双幂函数分区时,可以将接近起始时间的区域分区更小,提高精度,从而使得不同截止期的消息可以分配到不同的母区间,有效减少了截止期相近的的消息被分配到同一个母区间内的概率。与平均分区相比,调度的条件也变得更加苛刻,这是保证消息实时性所必须要达到的前提条件。 在上一章节,借助量化误差的概念理论上给出了消息集可调度的判定准则,接下来我们通过系统模拟方式来验证是否满足可调度性。采用系统模拟方式简单易行,虽然结果不能完全反应系统的真实情况,但能够作为一种辅助手段去验证我们提出的双幂函数分区调度算法。 参考本文所提出的改进的EDF调度算法,采用CANoe平台进行仿真实验。CANoe的主要组成部分:模拟界面编辑、CANdb++编辑器、CAPL浏览器、面板设计等。目前市面上流行的几种总线,如CAN、LIN、FlexRay、以太网等,均可在CANoe上实现仿真测试。通过CANoe可以将所有节点虚拟化,对于各个节点相应的通信数据可以使用CANdb++编辑器建立所需要的数据库,并通过CAPL语言编写各CAN节点程序实现节点间的通讯、错误处理等。 此外,汽车工程师协会(SAE)提供了一个“基准”应用[9],其描述了在原型电动汽车上的7个不同子系统之间发送的一组信号。尽管这个汽车控制系统是使用点对点链路设计的,但是这组信号为说明CAN总线在复杂分布式实时控制系统中的应用提供了一个很好的例子,因此,针对于本次实验,我们将通过CANoe搭建出此网络通信模型。其中7个子系统分别是:电池(Battery),车辆控制器(V/C),逆变器/电机控制器(I/M C),仪表盘显示(Ins),驱动器输入(Driver),制动器(Brakes),变速器控制(Trans),如图3所示。 图3 节点示意图 连接这些子系统的网络需要处理总共53个信号,按照信号的接收方、发送方、信号周期以及信号长度等要求将信号打包成10个消息,如表1所示。根据表中信息,通过操作CANdb++,将所有信号打包封装,并且对该网络的相关参数进行配置,如波特率、采样点等。根据表1消息矩阵中消息的周期分布情况,同时在满足判定式(8)的前提下,可将分区中各参数选取为:a=2,k=16,q=8。 表1 消息矩阵 CAN网络中的节点在收发消息时,依据本文所提出的双幂函数分区EDF调度算法,利用CAPL编程对消息以及通讯进程进行动态处理,以实现合理的调度。具体实现过程如下:在本文的调度机制下,CAN节点在发送消息前,计算该消息的相对截止时间,然后依据所得相对截止时间算出对应的母区间和子区间号,将对应的区间号转换为消息的优先级并进行进制转换得到消息的标识符,再根据当前的标识符进行仲裁。部分程序设计如下所示: if(msg4.DIR!=TX) { t_new=timeNow()/100000.0+0.16; write("t_new=%f",t_new); D=d-t_new-init; count++; if(D>0.001&&D<62.5) { g=1; h=_floor(7-(1000.0/(16*D))); } else if(D>62.5) { g=_floor(5-exp(1000/D)); h=_floor((exp(6-g)*6*D-7000)/(exp(6-g)*D-1000)); } p=h+(g-1)*5; write("p4=%d",p); p=0x14-p; p=p<<18; 对于双幂函数分区调度算法的网络性能分析,我们主要将关注点放在最坏响应时间上,最坏响应时间是消息的最大时延,即消息在队列中的最长排队时间和传输时间的总和,因此实时性的强弱在数据上最直观的体现就是最坏响应时间的大小。其中,挑选出5组周期差别较大的消息通过对比平均分区方法来验证双幂函数分区的优越性。每组实验3次后计算“消息最坏响应时间”的平均值,实验结果如图4所示。 图4 消息最坏响应时间 结合实验结果,对比传统的基于平均分区EDF调度算法,我们可以发现本文提出的基于双幂函数分区方法所具有的优点: 1)针对于消息集的截止期,采用传统的平均分区EDF调度算法(分区大小为2 ms),在对标识符进行编码时至少需要7位才能够满足编码要求,而采用本文的方法,只需要6位就可以满足需求。 2)通过计算可以得知,在本文的试验参数下,最小的子区间大小约为0.05 ms,相较于平均分区的2 ms,明显提高了分区精度,换言之,在经历一段时间后,消息的截止期在不断地减小,那么仍然会导致多个消息的截止期落在同一个分区内,从而获得同样的优先级,而本文的双幂函数分区方法可以将截止期划分至微秒级,从而保证了较高的辨识度。 3)采用双幂函数分区的EDF调度算法,可以降低消息集的最坏响应时间,从图5中可以观察到20 ms以内的消息,即高优先级消息,最坏响应时间的减少尤为明显,这也验证了第二点,双幂函数分区现在对较小的截止期上依然保证了很强的辨识度。 显然,通过双幂函数分区的方法进行调度,分区误差进一步减小,对于截止期最终落在哪个分区更为精确,降低了因优先级反转而无法调度的情况,使得消息的最坏响应时间得到了有效的缩减,从而提高了网络传输的实时性。 本文对比平均分区EDF调度算法,对于量化误差引起的消息不可被调度问题,引入一种双幂函数分区的方法。理论分析量化误差对该方法的影响,并论证了该方法使用时消息可调度的判定条件。实验证明了本文的双幂函数分区调度算法对消息的截止周期进行合理的分配,从而克服了传统EDF算法在调度方面的不足,优化了消息的最坏响应时间,提高系统实时性,对于EDF调度算法在实际中更好的应用于CAN总线通信优化中起着指导作用。2 双幂函数分区EDF算法
2.1 双幂函数分区的EDF算法
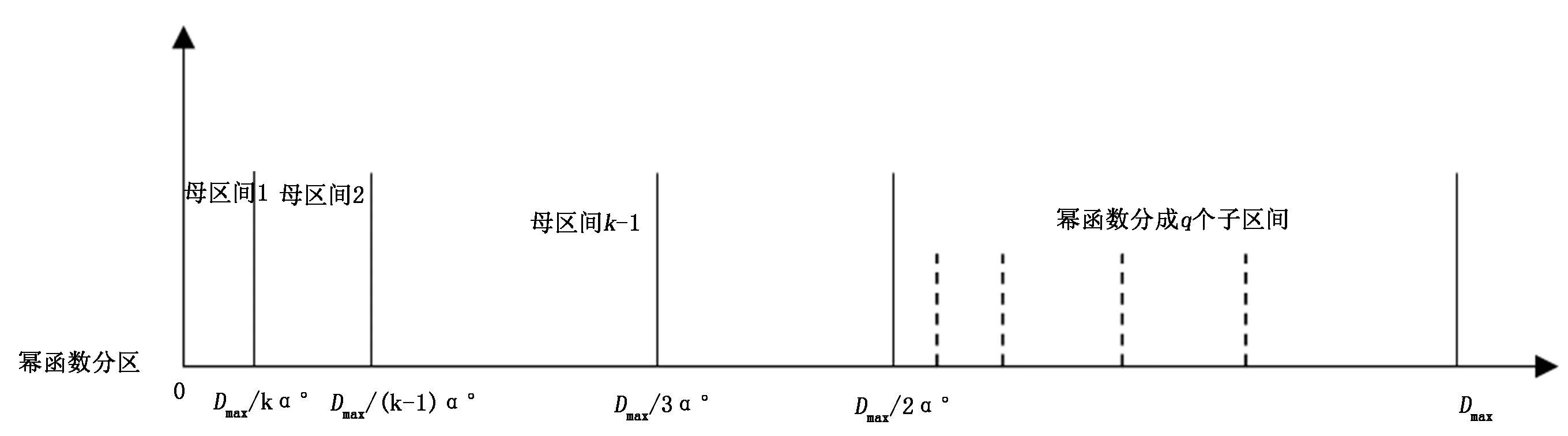
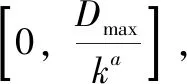
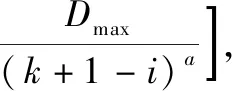
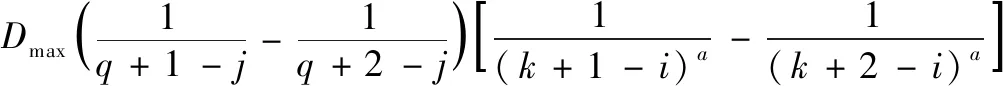
2.2 可调度性分析
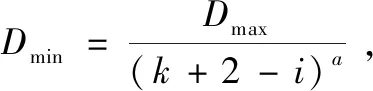

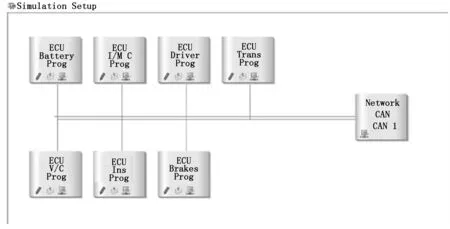
3 实验验证与分析
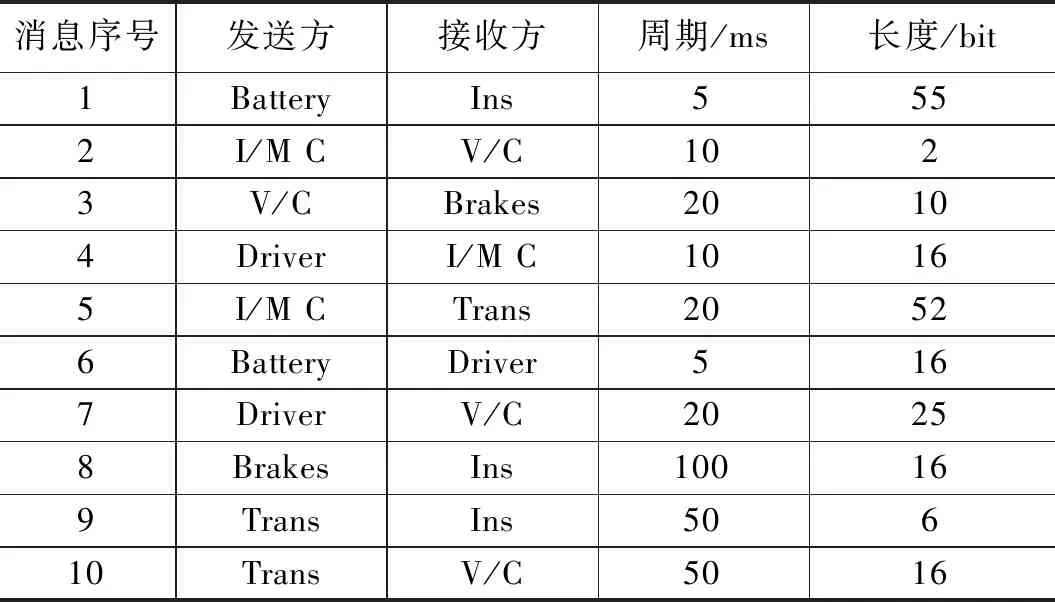
4 结束语
