基于GNSS移动基线的列车完整性监测

姜 维，刘永强，王 剑*，张文彪

(1.北京交通大学a.电子信息工程学院，b.轨道交通控制与安全国家重点实验室，c.北京市电磁兼容与卫星导航工程技术研究中心，北京100044；2.中电科西北集团共性技术分公司，软件产品部，西安710068；3.中国铁路青藏集团有限公司电务部，西宁810007)

0 引 言

列车各节车厢是通过车钩钩缓装置物理连接在一起的，在列车前进过程中，需要频繁的加速和制动，长时间的作用会损坏车钩，故车厢之间存在脱钩的风险[1].一旦列车脱钩，列车完整性监测系统应立即给出报警信息，避免列车脱轨或与后车碰撞等事故发生.因此，列车完整性监测是列车运行控制系统的重要部分，对保证列车完整，避免追尾甚至脱轨事故的发生具有重要意义.

被广泛使用的列车完整性监测方式包括风压检测和轨道电路占用检查两种方式.下一代列车控制系统(NGTC)，需要减少轨道电路等轨旁设备的依赖[2].文献[3]设计了一种基于GNSS 及无线通信的列车完整性监测系统，通过车长的比较进行列车完整性监测，并加入虚拟卫星，以克服列尾设备的可见卫星数目少的问题.文献[4]采用基于GPS及速度传感器的列车定位系统实现列车完整性监测.文献[5]针对基于GPS 及IMU的列车完整性监测系统，提出基于模糊逻辑的列车完整性检测方法，通过计算列首及列尾的相对车长、速度及加速度判断列车完整性状态.文献[6]提出GNSS伪距差分的方法用于列车完整性监测，但需要轨道数据库等约束信息.上述基于车长的列车完整性检测方法误差均在10 m 左右，不仅存在虚警及误警的安全隐患，也不利于铁路运输效率的提高.

为进一步减小解算车长的误差，本文提出一种基于GNSS移动基线的列车完整性监测方法.与伪距定位相比，载波相位定位具有更高的精度.在解算移动基线时，为得到高精度的基线长度，同时避免对误差进行复杂的建模估计，采用双差载波相位的解算方式，消除卫星和接收机的时钟误差，电离层和对流层等与传播路径相关的误差.建立双差载波相位的观测方程，用卡尔曼滤波算法估计移动基线长度，所得结果与参考车长进行比较，实现列车的完整性监测.

1 GNSS移动基线模型

基线是指两个天线之间构成的位置矢量.一般基线包括静态基线和动态基线两种：静态基线一般安装在固定静态结构体，用于桥梁、大坝、高大建筑等的变形监测；动态基线一般安装在移动载体上，用于舰船、飞机、导弹等载体的定向和姿态测量.本文将天线固定在列车的两端车厢，在列车行驶过程中，基线会随列车的前进而移动，计算移动基线长度实现列车完整性状态监测.

图1为列车完整和脱钩两种情况下，移动基线的示意图.通过解算得到两天线之间移动基线长度，与参考车长进行比较，判断列车的完整性状态.

图1 移动基线示意图Fig.1 Moving baseline diagram

基于移动基线的完整性判断流程如图2所示，包含以下4个步骤：

Step 1相对位置计算，通过双差载波相位模型和卡尔曼滤波解算两天线的相对位置.

Step 2基线长度计算，在已知两天线相对位置的基础上，用两点间距离公式得到基线长度L.

Step 3比较判断，已知基线参考长度与阈值η，判断基线与参考车长的偏差是否在阈值范围内.

Step 4得到完整性状态，解算长度在阈值范围内，则说明列车完整性状态正常；反之，则列车完整性状态异常，系统应给出报警信息.

图2 列车完整性判断流程Fig.2 Train integrity judgment process

基于以上列车完整性监测方法，不依靠轨道电路、差分基站等地面设备，实现实时列车完整性监测.

2 移动基线解算的数学模型

2.1 双差载波相位原理

载波信号的传播路径如图3所示，但其测量值受卫星钟差，接收机钟差，电离层延迟误差和对流层延迟误差等误差源影响.

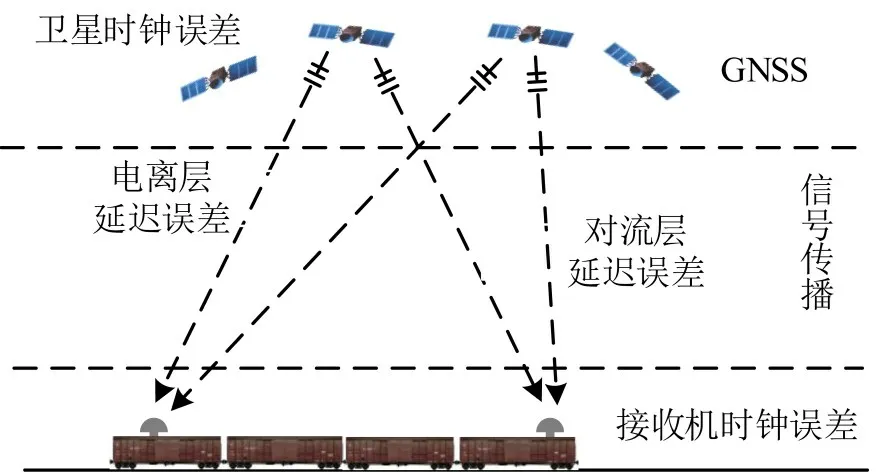
图3 载波相位定位误差Fig.3 Carrier phase positioning error

根据载波信号传播过程，列首和列尾两接收机的载波相位观测方程为

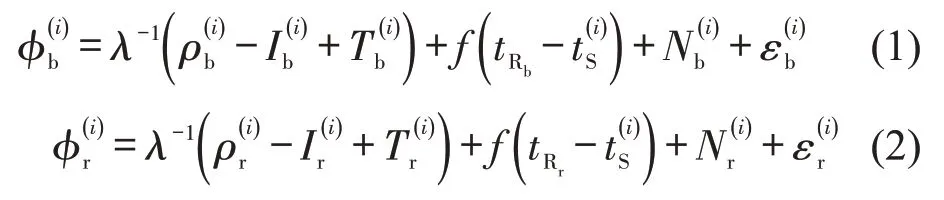
式中：φ为载波相位测量值；λ为载波信号的波长；ρ为卫星到接收机的真实距离；I为电离层延迟误差；T为对流层的延迟误差；f为载波的频率；tR为接收机的钟差；tS为卫星的钟差；N为整周模糊度；ε为难以定量描述的误差总和，包括接收机噪声等；i为第i颗卫星；b,r分别为基准站和辅助站.

列车两端天线间的距离很短，故载波信号从卫星传播至两天线的路径几乎一样，在两天线之间做差可以基本消除卫星钟差的影响和传播路径引起的误差，包括电离层和对流层的延迟误差.对式(1)和式(2)间做一次单差，得到的载波相位的单差方程为

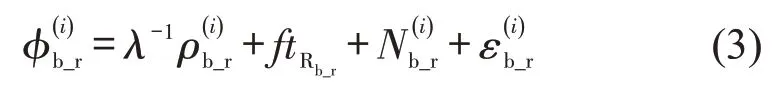
式中：下标b_r代表基准站和移动站两接收机间做差.

类似地，假设两接收机同时跟踪到另一颗卫星j，可得到载波相位的单差方程为

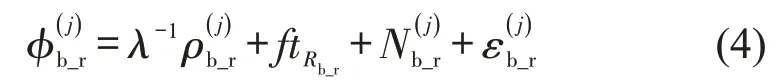
对同一个接收机而言，在卫星之间再次做差后，可以消除接收机的钟差等与接收机有关的误差.对式(3)和式(4)做星间差分得到双差观测方程为

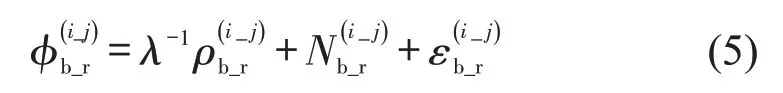
式中：上标i_j代表在第i颗星和第j颗星之间做差.

需选定一个天线作为基准天线，另一个作为辅助天线.假定基准天线地理坐标为(xb,yb,zb)，辅助天线的概略坐标为，本文基线长度远小于天线和卫星之间距离(约20 200 km)，故可选用基准天线b的位置作为天线r的概略位置，将辅助天线r到卫星的距离在其概略位置处一阶泰勒展开，可得

一阶泰勒展开系数表示基准天线指向卫星的方向余弦，定义3个轴向余弦分别为(l,m,q)，则有

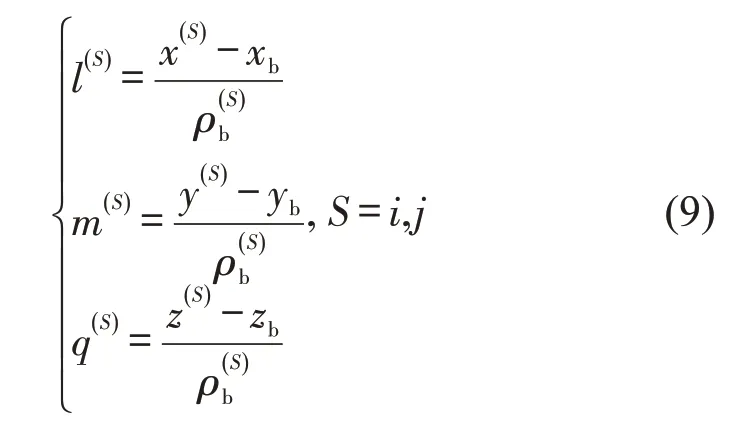
将式(7)～式(9)代入式(6)可得

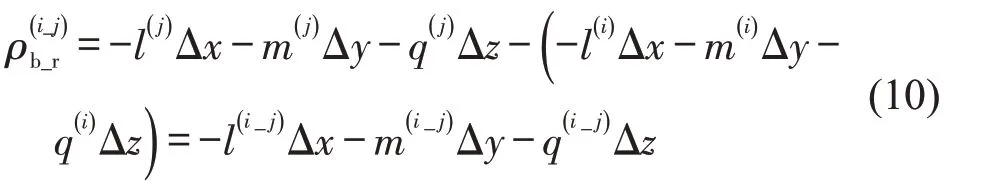
将式(10)代入式(5)，得到

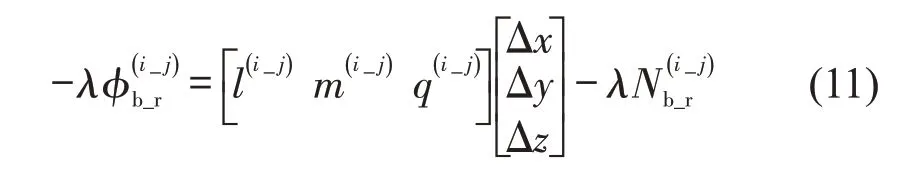
假设当前历元中，两接收机同时观测到卫星数目为n，选取一颗参考卫星，则可得到(n-1)个载波相位的双差方程，写成矩阵形式为

式中：φ为载波相位双差值组成的矩阵；为轴向余弦(l,m,q)组成的矩阵；N为模糊度组成的矩阵.三者的维度都是(n-1).

式(12)中只有基线向量X和双差整周模糊度N是未知的，用卡尔曼滤波算法求解.

2.2 卡尔曼滤波解算基线位置矢量

卡尔曼滤波系统模型为

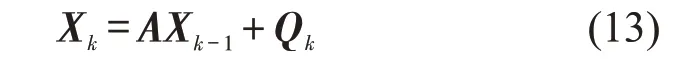
式中：Xk为k时刻系统状态矢量；A为状态转移矩阵；Qk为系统过程噪声.

系统状态维度为6+(n-1)，包括3个方向的相对位置，相对速率，以及双差整周模糊度.

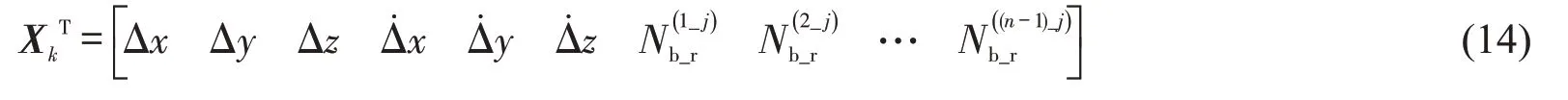
状态转移矩阵为

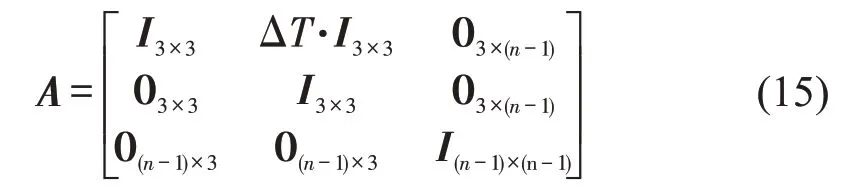
式中：I为单位矩阵；0为零矩阵；ΔT为时间间隔，ΔT=0.1 s.

系统噪声矩阵为

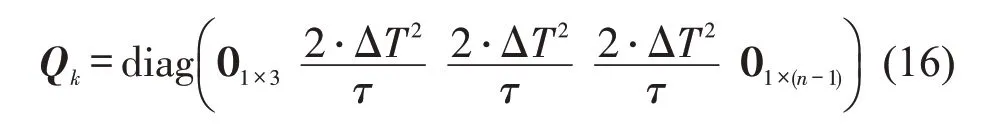
式中：τ为相关时间.

系统测量模型为

式中：Zk为系统观测向量；Hk为量测矩阵；Vk为高斯白噪声，对应协方差矩阵为R.

系统观测矢量为

系统测量矩阵为

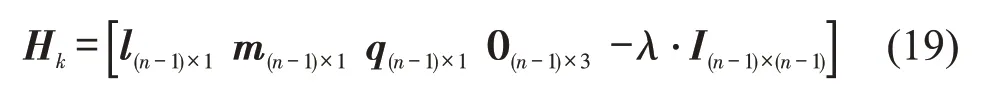
式中：(l,m,q)为(n-1)余弦参数(l,m,q)的差组成的矩阵.

噪声协方差矩阵为

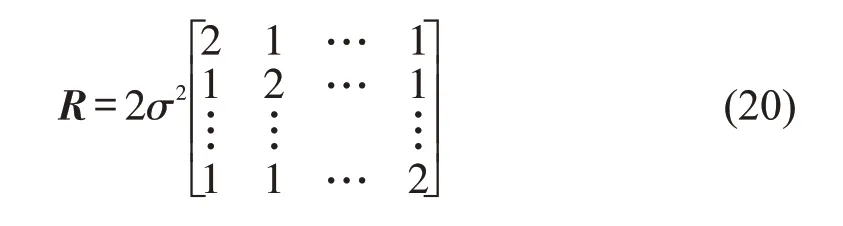
式中：参数σ为L1 载波噪声的标准偏差，取值为0.000 8 m[7].

2.3 数据处理流程

根据2.1节和2.2节，移动基线解算数据流程如图4所示，分为以下步骤：

Step 1根据式(3)，在两天线之间作一次单差，消除卫星的钟差，电离层延迟误差和对流层延迟误差的影响.

Step 2根据式(5)，在其他卫星与参考卫星之间再次作差，消除接收机钟差的影响.

Step 3根据式(13)～式(20)，用卡尔曼滤波估计每个时刻两天线之间的相对位置矢量，相对速度，以及双差整周模糊度.再利用两天线之间的相对位置计算得到基线的实时长度.

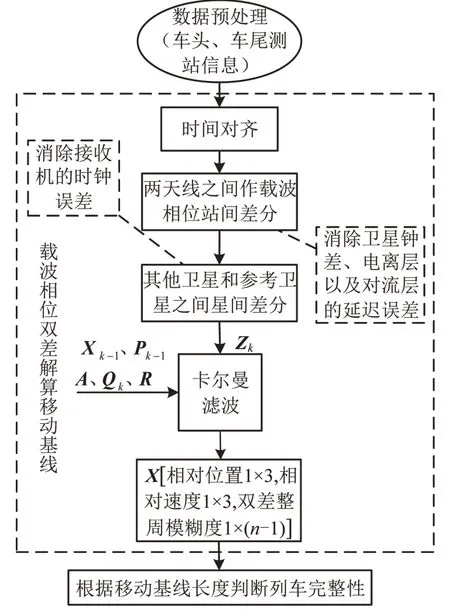
图4 移动基线解算的数据流图Fig.4 Data flow diagram of moving baseline solution

2.4 选择参考卫星及卫星变化处理

(1)选择参考卫星.

2.2节在卫星之间作第二次载波相位差分时，必须人为选定一颗卫星作为参考.一般高度角越大的卫星对应的观测值误差越小[8]，依次计算每颗卫星的高度角，选出高度角最大的一颗卫星作为参考卫星.

计算卫星高度角时，先计算卫星在车头天线处的载体坐标系下的坐标，转换关系为

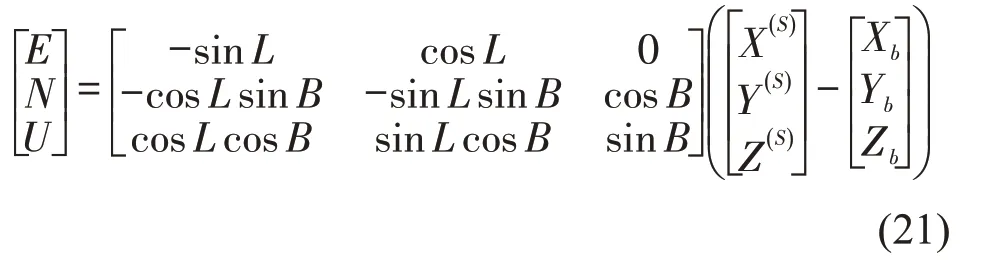
再计算卫星在车头天线处的高度角为

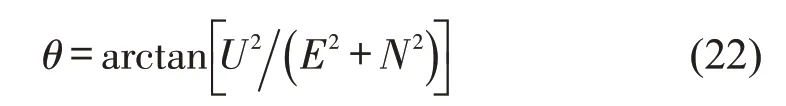
(2)卫星变化的影响及处理.

在列车实际运行过程中，跟踪到的可见卫星是不断变化的，对应卡尔曼滤波状态矩阵X和误差协方差矩阵P也要随之改变.卫星变化分以下3种情况：

①卫星减少.

此时，可见卫星与上一时刻相比，在状态矩阵和协方差矩阵中去掉与失锁卫星对应的值，再进行滤波解算.

②卫星增加.

Step 1根据上一时刻可见卫星对应的矩阵滤波，得到当前时刻两天线的相对位置(Δx,Δy,Δz).

Step 2根据式(11)，用当前时刻相对位置反解增加卫星对应的双差整周模糊度

Step 3用Step 2 得到的更新状态矩阵X；协方差矩阵P则保留对应位置和速度部分，其余部分全部初始化.

Step 4将Step 3得到的X和P先滤波一次，进行平滑处理，再供下一时刻滤波使用.

③卫星减少同时增加其他卫星.

先根据①作减星处理，再根据②作加星处理.

3 验证及分析

为验证本文所提算法的有效性，选用2018年6月京沈高铁试验段数据进行实验验证.选取数据时长近10 min，列车行驶约32.5 km.列车实际运行轨迹如图5所示，位于黑山北站和新民北站中间，该段现场线路的试验场景开阔，卫星信号质量良好.

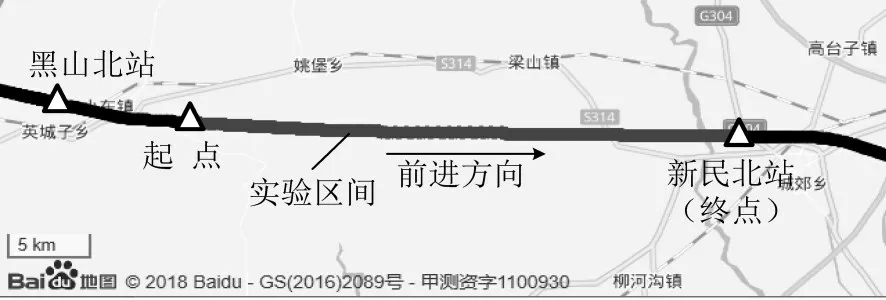
图5 列车行驶轨迹Fig.5 Test train trajectory

试验列车为复兴号列车，如图6中(a)图所示.在头部车厢和尾部车厢顶部放置导航卫星信号接收天线，经过测量，两天线间绝对长度为186.9 m.将两天线间的绝对距离作为解算结果的对比参考值.

图6 实验列车和车载接收机Fig.6 Test train and on-board equipment

图7中：上图为实验过程中公共可见卫星数，下图为对应每个时刻的位置精度因子(Position Dilution of Precision，PDOP)值.可以看出，整个实验过程中，卫星数频繁变化，但多数情况下有8颗公共可见卫星.PDOP值反映整个过程中可见卫星的分布情况，可以看出，可见卫星数目越多，对应的PDOP值越小.整体可见卫星状况良好，图7中虚线框圈出部分，卫星数目略有减少，这是因为列车进新民北站停车，车站顶棚的遮挡使跟踪到的卫星数目减少.移动基线长度解算结果如图8所示.与参考长度比较，误差结果如图9所示.整体而言，解算结果达到预期效果，最大误差不超过0.5 m.

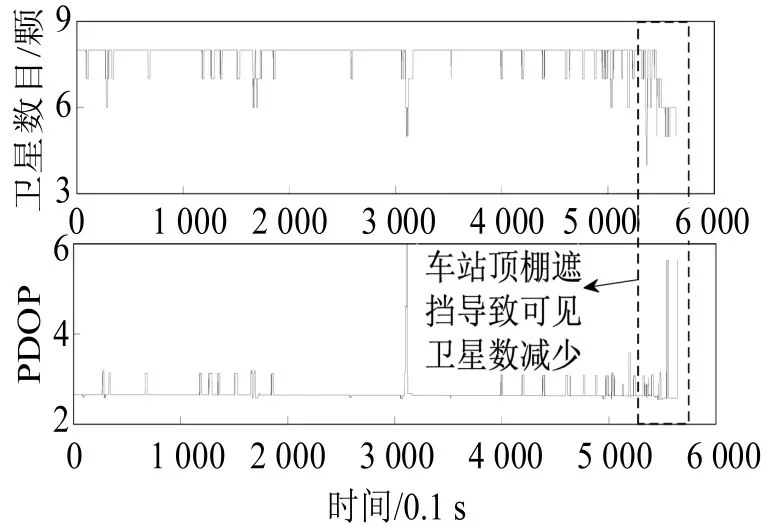
图7 可见卫星数和PDOP值Fig.7 PDOP and visible satellites number

图8 解算结果与参考长度比较Fig.8 Comparison of solution results with reference length

图9 基于移动基线解算结果误差Fig.9 Error based on moving baseline solution results

解算初始阶段，由于卡尔曼滤波收敛需要时间，解算结果出现明显震荡.解算结果曲线整体不够平滑，这是因为整个过程中可见卫星频繁变化，对应卡尔曼滤波的状态矩阵X和误差协方差矩阵P需要重新初始化，而初始化值无法准确给定.在5 300 历元以后，误差明显增大，对比图7可见卫星数目可以看出，这是因为可见卫星数目减少导致的.

实验过程中使用的两款接收机均为高精度接收机，为进一步说明所提算法的优越性，用单点定位结果作为对比实验，结果如表1所示.整体来看，基于移动基线的平均误差为0.3 m，基于单点定位的平均误差为0.7 m.

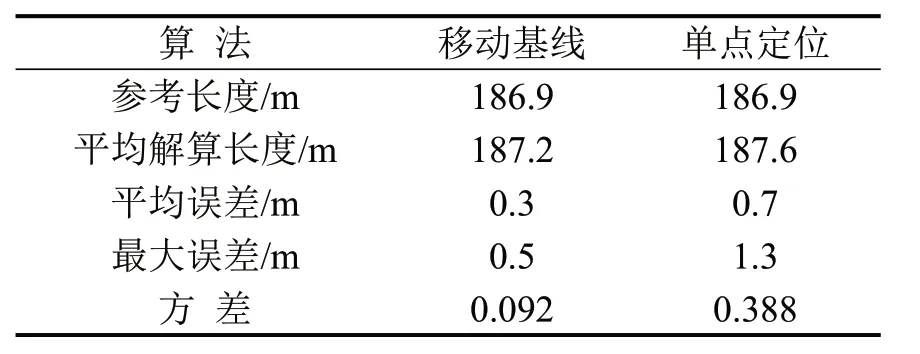
表1 移动基线与单点定位计算结果比较Table1 Comparison between moving baseline and single point positioning

两种结果对比如图10所示，整体而言，基于移动基线的结果比单点定位的结果更平稳，连续性更好.特别当可见卫星数目明显减少时，基于单点定位的误差增大更加明显，达到1.3 m，而基于移动基线的误差约为0.5 m，说明移动基线的结果优于单点定位的结果.

图10 移动基线和单点定位的结果比较Fig.10 Comparison of calculation results between moving baseline and single point positioning

4 结 论

本文提出一种基于GNSS 移动基线的列车完整性监测方法.为得到高精度的基线长度，引入载波相位双差方法计算移动基线长度.建立双差载波相位的双差观测方程，用卡尔曼滤波算法动态估计基线的相对位置，得到移动基线的实时长度，与参考车长进行比较，监测列车完整性状态.京沈高铁试验结果表明，移动基线长度误差在0.5 m以内，较之前基于车长的完整性监测方法性能有明显提升，证明将GNSS移动基线用于列车完整性监测的有效性.

本文仅使用GPS数据进行算法验证，后续考虑引入北斗系统，进一步提高系统的精度和稳定性；此外，进一步结合风压、惯导等建立高精度、高可靠性的列车完整性监测系统.