多重边融合复杂网络的间歇式量化同步分析
2020-09-01洪雅娴黄振坤宾红华
洪雅娴,黄振坤,陈 超,宾红华
(集美大学理学院,福建 厦门 361021)
0 引言
目前,许多学者对于复杂网络的研究多是针对单边、单一性质的网络[1-10]。如:文献[11]在随机选择的点对点之间添加了较低的快捷方式,给出了小世界网络平均路径长度和模型中路径长度分布的均值场解;文献[12]通过一个标量传输信号,解决了驱动型混沌系统的自适应同步问题;文献[13]提出了一种具有时变时滞的线性混合耦合网络,对网络的全局同步进行了进一步的研究。但现实生活中包含大量的由多种性质子网络构成的多重边融合复杂网络(complex networks with multi-links,MLUCN),这方面也引起了研究者的广泛关注[14-16]。
研究复杂网络的同步问题是很重要的一个课题[1],自适应控制法[2-5]、滑模变结构同步法[6]、(鲁棒)脉冲同步控制法[7-8]、耦合矩阵反馈[9]和分散反馈控制[10]等在基于连续时间内耦合网络的同步问题得到广泛应用。但实际上常常由于信道堵塞、频率改变、延时等因素,网络节点发生脉冲式间断,现实世界中常常是不连续时间的耦合网络,故本文考虑间歇式的耦合网络。同时,量化作为网络控制系统中必不可少的环节,在转换时会产生量化误差,由于这种误差有网络诱导时延、数据丢包、带宽约束等因素的影响[17],使得网络控制系统中对量化影响的研究比较困难。目前,一些学者已经考虑到了量化问题:文献[18]引入量化器对具有数据包丢失和混合时滞的Markov切换离散型复杂网络的可稳性和可同步性问题进行了分析;文献[19]将量化和触发误差融合在一起,讨论Lurie形式在有限信道下驱动响应系统的同步问题;文献[20] 在传输前对耦合信号进行量化,并将量化误差转化为扇区有界的不确定性,考虑了一类具有交换拓扑和量化效应的复杂网络的非脆弱H∞估计问题。
由于网络的节点之间往往存在多重性质,因此,MLUCN得到广泛关注[14-16]。文献[14-15] 应用自适应方式研究MLUCN的同步问题,文献[16]提出了一个MLUCN的动态演化模型。然而量化因素在现有的MLUCN研究中往往被忽略了,量化同步在多重边融合网络中很少有相关报道。本文引入网络拆分[14-16]的思想,根据节点间信息传输速度的不同,引入时滞对多重边网络进行拆分,并考虑到量化转换过程中产生的误差,采用了对数量化器来控制。为了节约信道资源和带宽,只在一个周期内的部分时间添加控制器,首次研究具有间歇式多重边融合的复杂网络同步分析。
1 模型描述

(1)
其中:xi=(xi1,xi2,…,xin)T∈Rn为第i个节点的状态变量;f:Rn→Rn为连续非线性函数;常数εl>0为第l个子网络的耦合强度;Γl∈Rn×Rn为第l个子网络中各节点状态变量之间的内部耦合矩阵函数;τl为第l个子网络相对于零子网络的时滞时间。

本文目的是设计合适的控制器ui(t),使得网络(1) 的状态指数收敛到如下同步域:x1(t)=x2(t)=…=xN(t)=s(t),
(2)

(3)
控制输入ui(t)设计为如下反馈控制器:ui(t)=-kiq(xi(t)-s(t))=-kiq(ei(t)),
(4)
其中:i=1,2,…,N;ki为待设计的反馈控制系数。
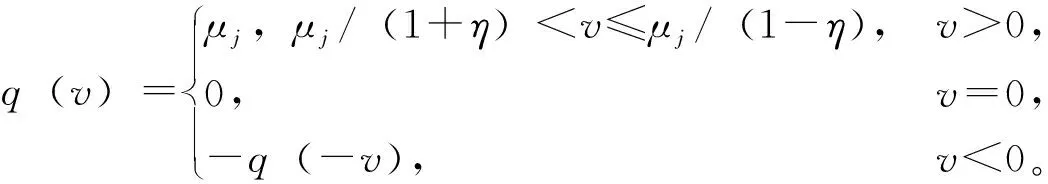
(5)
其中:μj构成q量化水平集S={±μj,μj=ρjμ0,j=0,±1,… }∪{±μ0}∪{0},0<ρ<1,μ0>0;v为量化器的输入;q(v)为量化器的输出;Δ为量化器q(·)的量化同步误差;η为参数,且满足η=(1-ρ)/(1+ρ),显然有q(v)-v=Δv,且Δ∈[-η,η]。
为便于叙述,将误差系统(3)表示为如下矩阵张量积的形式:
(6)
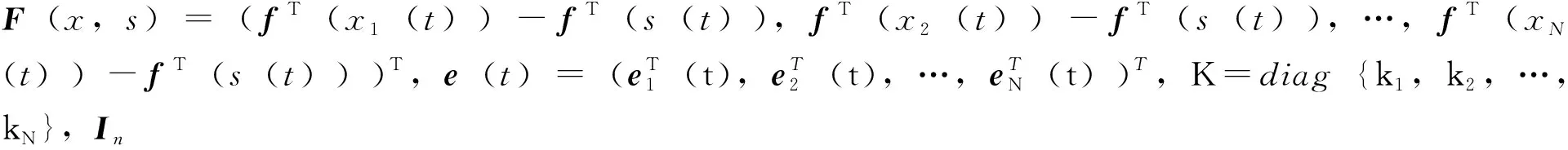

注1 条件(H1)通常被称为全局Lipschitz条件,Li是Lipchitz常数,容易知道许多复杂网络系统都能满足(H1)。
注2 条件(H2)利用比较定理易证得。
2 主要结果

证明构造如下Lyapunov函数V(t)=eT(t)e(t)/2。
(7)
对V(t)沿系统(6)求导,当dT eT(t)e(t)/2+eT(t)(L⊗In)T(L⊗In)e(t)/2≤ λmax(INn+(L⊗In)T(L⊗In))V(t)= λ1V(t)。 两边积分可得V(t)≤V(dT)exp(λ1(t-dT))。 (8) 当dT+δ eT(t)F(x,s)+ε0eT(t)(B(0)⊗Γ(0))e(t)+ε1eT(t)(B(1)⊗Γ(1))e(t-τ1)+ …+ εm-1eT(t)(B(m-1)⊗Γ(m-1))e(t-τm-1)-eT(t)(K⊗In)q(e(t))≤ eT(t)(INn+(L⊗In)T(L⊗In))e(t)/2+ε0eT(t)((B(0)⊗Γ(0))/2+ (B(0)⊗Γ(0))T)e(t)+eT(t)(ε1(B(1)⊗Γ(1))(B(1)⊗Γ(1))T/2+…+ εm-1(B(m-1)⊗Γ(m-1))(B(m-1)⊗Γ(m-1))T)e(t)/2+(ε1eT(t-τ1)e(t-τ1)+…+ eT(t)((INn+(L⊗In)T(L⊗In)+ε0((B(0)⊗Γ(0))+ (B(0)⊗Γ(0))T)/2+ε1(B(1)⊗Γ(1))(B(1)⊗Γ(1))T+…+ (ε1eT(t-τ1)e(t-τ1)+…+εm-1eT(t-τm-1)e(t-τm-1))/2≤ λ2V(t)+ε1V(t-τ1)+…+εm-1V(t-τm-1), 由比较定理可知V(t)≤V(dT+δ)exp{-λ(t-(dT+δ))}。 (9) 当t=dT+δ时,由式(8)知V(dT+δ)≤V(dT)exp(λ1δ)。 (10) 从而当dT+δ (11) 1)当dT (12) 2)当dT+δ (13) 情形1 先对式(12)进行考虑,此时dT ⅰ)若λ+λ1≥0,有 V(t)≤V(0)exp(λ1t+d(λ+λ1)(δ-T))≤V(0)exp(λ1t+(t-δ)(λ+λ1)(δ-T)/T)= (14) ⅱ)若λ+λ1<0,有V(t)≤V(0)exp(λ1t+d(λ+λ1)(δ-T))≤V(0)exp(λ1t+t(λ+λ1)(δ-T)/T)= V(0)exp{(λ1+(δ/T-1)(λ+λ1))t}=V(0)exp{(δ(λ+λ1)/T-λ)t}≤ (15) 情形2 再对式(13)进行考虑,此时dT+δ ⅰ)若λ+λ1≥0,有V(t)≤V(0)exp(-λt+δ(d+1)(λ+λ1))≤V(0)exp(-λt+δ((t-δ)/T+1)(λ+λ1))= (16) ⅱ)若λ+λ1<0,有V(t)≤V(0)exp(-λt+δ(d+1)(λ+λ1))≤V(0)exp(-λt+δt(λ+λ1)/T)= (17) (18) 由于总可以选取合适的K使得δ(λ1+λ)/T-λ<0。由上述推导可知,误差系统(3)是指数型稳定的,即耦合网络(1) 在控制器(4)的作用下能够实现同步。 (19) 此时多重边耦合复杂网络模型为: (20) (21) 其中函数Λ(ei1)=|xi1+1|-|xi1-1|-|si1+1|+|si1-1|。 本文引入网络拆分的思想对多重性质的网络进行研究,利用Lyapunov稳定性理论并结合脉冲控制周期和量化器的特征,首次给出基于量化控制信号的间歇耦合多重边融合复杂动态网络同步化准则,所得结果是对文献[14-16]的补充和拓展。最后通过仿真实例证明了所得结果的有效性。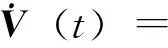

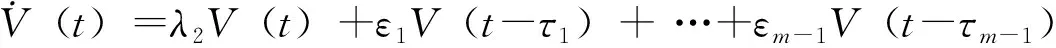

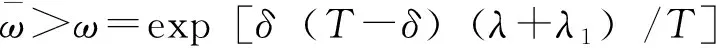


3 仿真实例







4 结论
