不确定移动机械臂的反演滑模轨迹跟踪控制

杨素珍

(漳州职业技术学院机械工程学院，福建 漳州 363000)

0 引言

移动机械臂是一类在移动平台上增加操作机械臂的系统[1]，该系统将移动平台的机动性和机械臂的灵活性相结合，操作空间大，可以完成单一移动平台或机械臂无法完成的复杂作业任务，因此移动机械臂的应用前景十分广阔[2-3]。轨迹跟踪控制是移动机械臂的核心控制内容之一，其控制移动机械臂跟踪给定时变参考轨迹，常见于移动机械臂工作任务轨迹规划后使用，可见轨迹跟踪性能直接影响工作任务完成效果，因此对移动机械臂轨迹跟踪控制器进行相关研究意义重大。

基于理想模型的常规控制器[4-5]已经不能满足轨道跟踪的控制需求，针对移动机械臂的轨迹跟踪控制，常规的有滑模控制方法，如文献[6]，但存在滑模抖振问题。为了减小滑模抖振影响，文献[7]结合自适应估计系统，研究了不确定上界的方法，但控制方法复杂度高，影响系统的实时性。本文研究一类移动机械臂的鲁棒轨迹跟踪控制，构建包含总体不确定性的移动平台和机械臂耦合动力学模型，以保证控制器在复杂环境中仍具备良好性能。

1 动力学模型分析

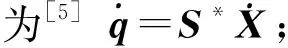
(1)

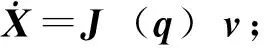
(2)

(3)

将式(1)求导代入式(3)，并将方程两边乘以S*T，得到移动臂的动力学模型为：

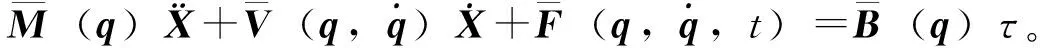
(4)

从式(4)可以看出，移动机械臂是一个复杂的多输入多输出耦合的非线性系统，同时由于采用非完整移动平台，无法实现输入-输出状态线性化，轨迹跟踪控制难度加大。

2 控制器设计与稳定性分析

首先采用非线性反馈

(5)

式中：U为辅助控制输入。

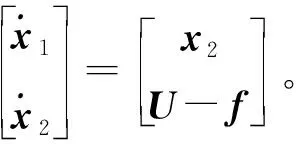
(6)

本文通过反演分步设计方法降低移动臂轨迹跟踪控制器的设计复杂度。

第一步 定义位置跟踪误差e1=x1-xr。

(7)

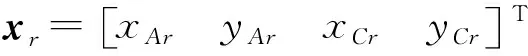
定义一种虚拟控制误差

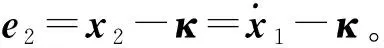
(8)

(9)

第二步 为了抵御系统复杂不确定性的影响，对控制器引入滑模鲁棒控制，设计切换项为

(10)

式中：k1为正定对角常数矩阵。

定义正定Lyapunov函数为V2=V1+(sTs)/2。

(11)

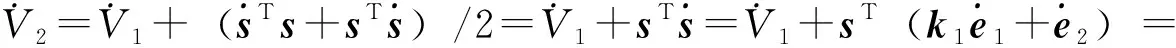
(12)

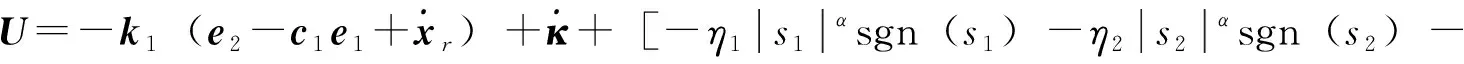
(13)

式中：η1、η2、η3、η4为正的常数；0<α<1。

定理：对于式(6)，如果满足假设1，则控制器式(13)可使得闭环系统渐进稳定。

证明：采用式(11)的Lyapunov函数，求导后将式(13)代入可得

(14)

文中控制器的结构图如图2所示，采用幂次趋近率有利于减小滑模控制的抖振现象。

3 仿真实验与分析

移动臂仿真模型物理参数取值为：移动平台的质量为m0=40kg；总惯量为J0=1.217kg·m2；车轮半径为r=0.1m；轮轴距为R=0.25m；机械臂连杆1的质量和长度分别为m1=5kg、l1=0.45m；机械臂连杆2的质量和长度分别为m2=3kg，l2=0.3m；连杆1和连杆2的转动惯量分别为J1=0.04kg·m2，J2=0.032kg·m2。

滑模控制器参数取：c1=diag(4,4,4,4)；k1=diag(2,2,2,2)；η1=5；η2=5；η3=5；η4=5；α=0.5。

常规PD控制器[5]跟踪结果如图3所示。本文控制器的轨迹跟踪结果如图4、图5所示。

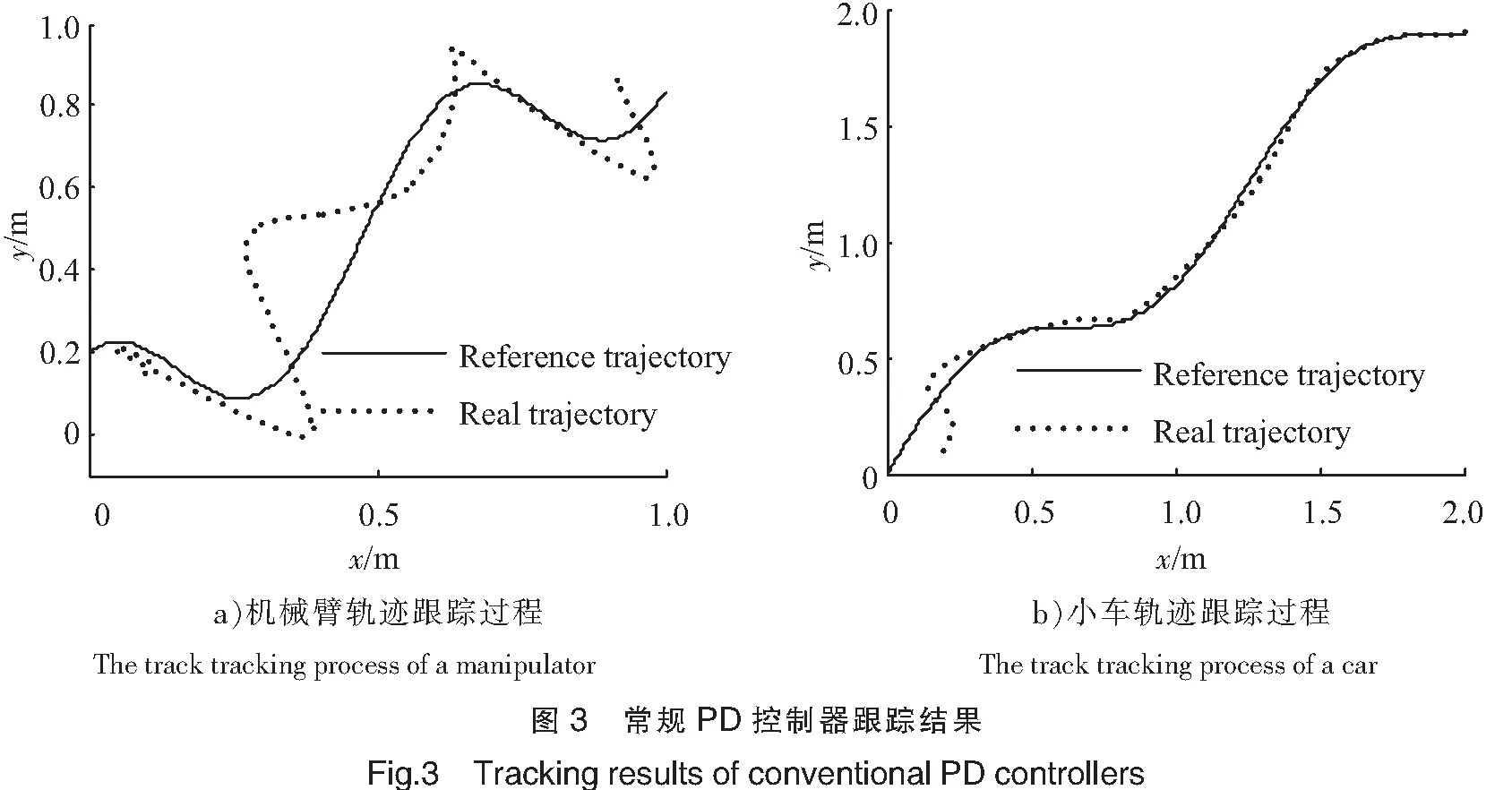
由图3可知，由于系统存在复杂不确定性，常规控制器无法消除其影响，轨迹跟踪误差较大。由图4、图5可见，滑模控制器的鲁棒性使得不确定性得到有效抑制，保证跟踪误差快速渐进收敛于零，可以满足复杂环境下移动臂较高精度的需求。

4 结束语

研究双轮驱动二连杆非完整移动机械臂的轨迹跟踪控制问题，构建系统不确定动力学模型，并应用输入-输出非线性反馈实现线性化。在此基础上，设计一种结合反演设计和滑模控制的轨迹跟踪控制器，并对滑模控制引入幂次趋近率，以减小滑模抖振现象。仿真结果表明，该控制器能有效抵御系统有界不确定性，跟踪速度快，精度高，可为高性能非完整移动机械臂控制器地开发提供有益参考。