轴测投影的若干问题

何援军

轴测投影的若干问题

何援军

(上海交通大学计算机系，上海 200240)

重新审视了轴测投影定义的表述。轴测投影法是用平行投影的方法，沿投射方向将空间坐标系投射到投影面上得到轴测坐标系并进而在这个坐标系下表述空间形体，用这种方法得到的图纸叫轴测图。三视图用3个视图分别表示形体的3个方向(面)，轴测图用一个视图同时表示三直三面角，其本质都是要表达出形体的3个方向(面)，在平面上表述空间形体。讨论了轴测投影中的一些根本问题，包括平行投影体系、轴测三角形、轴测投影体系、轴测投影的基本要素和基本公式，剖析了正轴测投影和斜轴测投影之共性和不同，给出了其原理图。

图学；平行投影体系；轴测投影；轴测图

这是论述大“图学”学科的第8篇文章[1-7]，本文主要讨论轴测投影中若干问题。

投影，是一种光线照射下形体在地面或墙面上有影子现象的模拟和抽象。其基本要素是形体、投射线和投影平面。所谓投影就是通过形体轮廓点的一系列投射线与投影面交点关系的集合。这是一种通过降维(投影)在平面上表示空间形体的办法。

通过物体的投射线向选定的面投射且在该面上得到图形的方法叫投影法，根据投影法所得到的图形叫投影。工程图常用的投影方法有以下 4种：多面正投影法、轴测投影法、透视投影法和标高投影法。

空间视角的基本条件是能同时看到物体的 3个面，因此用单面投影图表达一个形体的空间感觉，就要同时表述一个立方体的3个面，才接近于人们的视觉习惯，形象逼真，富有立体感。三视图用3个视图分别表示形体的3个面，轴测图用一个视图同时表示三直三面角(立方体任一个顶点由3个互相垂直的面相交而成)，其目标都是要表达形体的3个面。这，就是引入轴测投影体系得到轴测图的缘由。

轴测图是工程上的一个重要图纸类型，轴测图一般不能反映出物体各表面的实形，因而度量性差，同时作图比较复杂。因此，在工程上常把轴测图作为辅助图样以帮助读图，说明机器的结构、安装、使用等情况，在设计中，用轴测图帮助构思、想象物体的形状，以弥补正投影图的不足。

1 轴测投影体系

最早的轴测投影画法出现在英国[8]，奠基人是Wiliam Farish (1759–1837年)，1820年，他在英国哲学学会会刊上发表了题为“论等测透视图(On Isometrical Perspective)”的论文，明确提出了表现力较好的立方体的一个面投影表示法：“从立方体一条对角线上的无穷远点，向一个垂直于该对角线的平面投影”，这构成了等轴测投影法。这个设想的扩展构成了后来的轴测投影法，其建立在向空间平面作平行投影的基础上，建立了空间坐标系、投射方向、投影面三者之间的几何关系，构成了轴测投影体系。

1.1 轴测投影的基本定理

德国几何学家K•波克证明了波克定理：“平面上从一个点引出的任意3条(不共线的)线段，总可以作为空间3条互相垂直的相等线段的平行投影。”波克定理被称为轴测投影的基本定理，其不仅奠定了轴测投影的理论基础，也打开了研究轴测投影的道路。波克定理还定性地描述了轴测投影中各参数之间的互相关系：投影平面上轴测轴的各种位置(轴间角)和轴测单位的各种长度(轴向伸缩系数)是与空间坐标轴的各种位置和投射方向相对应的。当任意选定了轴向伸缩系数的比值和轴间角以后，总能求出空间坐标轴的位置和相应的投射方向。

1.2 平行投影体系

轴测投影建立在一个平行投影体系上。

平行投影体系。设在空间坐标系下表述的 一个平面，一个方向和任意一点。如果通过点引一条与方向平行的直线使其与平面相交，则交点就叫做点沿方向的平行投影。直线叫做投射线，平面叫做投影面。如果投影方向与投影面垂直，这种投影就叫做正投影，否则叫做斜投影。由空间坐标系、投影面和投射方向构成的一组元素叫做平行投影系，其表达空间坐标系、投射方向、投影面三者之间的几何关系。

1.3 轴测投影的表述

下面给出轴测投影的完整表述：

轴测投影法是建立在平行投影的基础上，将一个空间坐标系沿投射方向投射到投影面上，由空间坐标轴的三投影得到轴测轴，构成轴测坐标系，在这个平面轴测坐标系下表述表示三直三面角的空间形体。

因此，简单地说，轴测投影就是：用平行投影的方法，将一空间坐标系向设定的投影面投影，构成投影面上的轴测坐标系。在这个轴测坐标系下表示的空间形体的图形叫做轴测图。

如图1~4所示，空间笛卡尔坐标系，投影平面，投射线(图1~2投射线，同向1)，三坐标轴，，与的交点分别为，，。

在投影面上，空间坐标系原点在上的投影为1，空间三坐标轴(,,)在面上的三投影(11,11,11)构成轴测坐标轴，三者以1为原点，构成轴测坐标系。

若⊥，构成正轴测投影(图1~2，投射线与1重叠)；否则，构成斜轴测投影(图3~4，1//，*⊥)。

图1 正轴测投影体系原理图

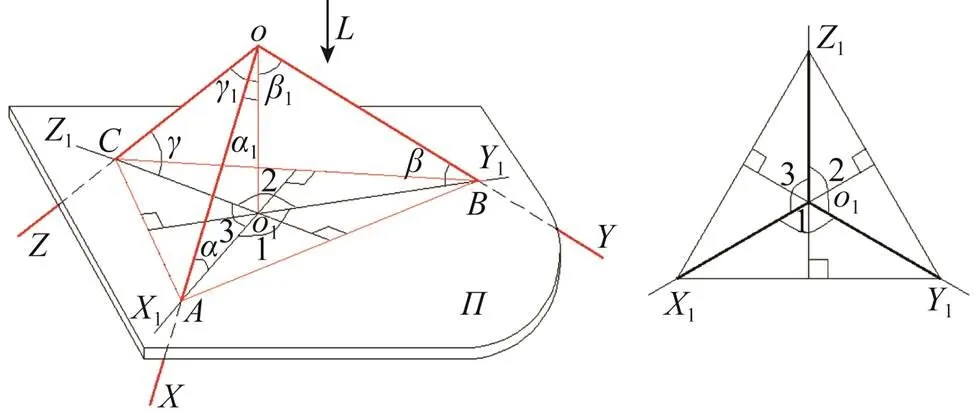
图2 正轴测投影要素关系

图3 斜轴测投影体系原理图

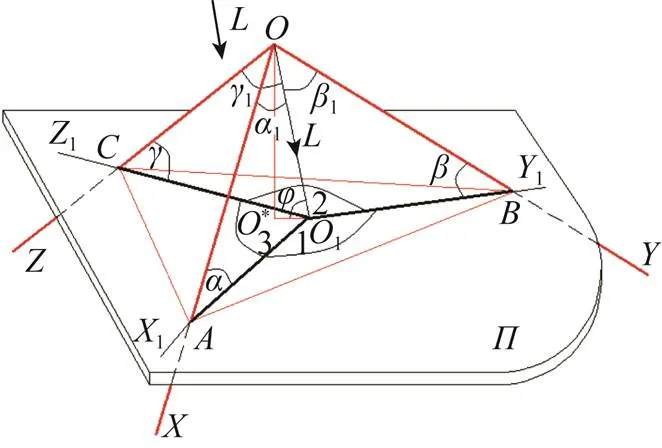
图4 斜轴测投影要素关系

1.4 轴测投影三角形

的3个坐标轴与的交点，，构成一个三角形△，称为“轴测投影三角形”，△是投影面与空间笛卡尔坐标系3个轴相交的交点形成的三角形，其与三直三面角的空间坐标系的3个坐标面构成一个四面角-。

这个△在轴测投影理论与应用的研究中有特别的意义。以后关于轴测投影的研究基本上是基于这个轴测投影三角形展开的。

1.5 轴测投影的基本术语

除了轴测投影三角形以外，在研究轴测投影中，还将用到下列术语。

(1) 轴测轴。空间三坐标轴(,,)在投射方向()下在投影面()上的投影为轴测投影轴，简称轴测轴(11,11,11)。

(2) 轴间角。相邻两轴测轴间的夹角称为轴间角(∠1, ∠1和∠1)。

(3) 轴测量度。形体的投影所反映的长、宽、高数值是沿轴测轴1，1，1来测量的。

(4) 轴向变形系数。沿轴测轴方向线段的投影长度与其真实长度之比，称为轴向变形系数，即

轴的轴向变形系数η＝1；

轴的轴向变形系数η=1；

轴的轴向变形系数η＝1。

2 轴测投影体系参数的决定

轴测投影体系表述空间坐标系、投射方向、投影面三者之间的几何关系。轴测投影体系也由这三者决定，其基本参数分为空间参数和轴测参数(参阅图1~4)。

(1) 空间参数。三直三面空间坐标系、投射方向、投影面。其中，和都是在下表达的。空间参数包括，，与1，1，1和等7个参数。投射方向与空间坐标系的互相位置由1，1，1确定。空间坐标系与投影面的互相位置由，，确定。投射方向与投影面的互相位置由确定。

(2) 轴测参数。轴向变形系数η，η，η和轴间角∠1，∠2，∠3等共6个参数可称为轴测参数。其是在轴测投影图上决定物体空间形状的作图依据。知道了轴间角和轴向变形系数，就可以沿着轴向度量形体的尺寸，也可以沿着轴向量画出形体上各点、各线段和整个形体的轴测投影。

2.1 用几何方法决定轴测投影参数

平行投影系的关键是投影面和投影方向，因此，在改变或确定这两个因素之后，轴测投影三角形△也就确定了，从几何的角度可以看到，轴测投影△一旦确定，轴测投影系中其他的相关参数也相应确定，参阅图1~4。其中，图2和图4只是图1和图3从不同方位看的同一图，图2是正轴测投影三角形的平面图。

(1) 首先，空间笛卡尔坐标系是确定的。

(2) 一旦投影面确定，空间笛卡尔坐标轴，，与面的交点，，就决定了，轴测投影△也就决定了(△1，△1和△1是共点的3个直角三角形)。

(3) 投射方向，空间坐标系原点到投影面(△)的投影1就决定(1=∠1，1=∠1，1=∠1为投射线1的方向角)。

(4)1一经确定，空间坐标系在面上的投影1，1，1也就确定了。由此，轴测轴(轴测坐标系确定)：

①投影面上的轴测轴1，1，1是确定的，从而轴间角∠1，∠1和∠1是确定的。

②变形比例(轴向变形系数)1，1，1是确定的。

③轴间角∠1 (∠1)，∠2 (∠1)和∠3 (∠1)确定的。

用几何方法决定轴测投影参数既是定性的，但也可以通过空间几何求交算法定量求得。

2.2 轴测投影参数的解析关系

轴测投影体系都是在笛卡尔直角坐标系下讨论的，这使得轴测投影参数可以用解析式表示和计算。空间7个参数和轴测6个参数(参阅图1~4)不全是独立的，其间有一些制约关系。下面先列出这些轴测参数间相互关系的主要解析式。其中，式(1)被称为轴测投影体系的基本公式。

(1) 各轴测参数满足下列约束

(ηηsin∠1)2+(ηηsin∠2)2+(ηηsin∠3)2

=η2+η2+η2–1 (1)

∠1+∠2+∠3=360° (2)

(2) 各空间参数满足下列约束

cos×cos1+cos×cos1+cos×cos1=sin(3)

cos2+cos2+cos2=1 (4)

cos21+cos21+cos21=1 (5)

cos×cos1+cos×cos1+cos×cos1=sin(6)

(3) 空间参数和轴测参数间的约束

η2+η2+η2=2+co2或η2+η2+η2=1+1/sin2(7)

(ηηsin∠1)2+(ηηsin∠2)2+(ηηsin∠3)2=csc2(8)

下面对上述轴测投影参数的8个关系式作出一些说明。

①对式(7)和式(8)的证明。

②基本式(1)的证明。基本式(1)的证明是在式(7)和式(8)的基础之上完成的，式(7)说明3个轴向伸缩系数的平方和是的函数，式(8)说明变形系数和轴间角也是的函数。先认定式(7)和式(8)成立(证明比较长，列在后面，作为参考)，证明基本式(1)。联立式(7)和式(8)，从中消去。就推导出基本式(1)。

基本式(1)反映了轴测投影中各轴测参数之间的定量关系。

③轴测投影体系的自由度。根据式(1)~(8)的约束，空间的7个参数有5个是独立参数，有 4个自由度，只要任给出其中4个独立参数，就能求出其余空间参数，从而也就能确定轴测系统的位置。

在基本式(1)中，3个轴间角只有2个是独立的，那么基本式本身也只包含有5个独立参数，只要任给出其中4个独立的轴测参数，就可以确定其余的参数。

这说明了一般形式的轴测投影体系有4个自由度。

④轴测投影体系的特例——正轴测投影。再来看轴测投影中的一个特例当投射方向与投影面垂直，即投射角=90°时，就是正轴测投影，此时式(7)可化简为

η2+η2+η2=2 (9)

将其代入基本式(1)，就得到

(ηηsin∠1)2+(ηηsin∠2)2+(ηηsin∠3)2=1 (10)

这就是正轴测投影基本定理。

3 常用轴测投影体系

轴测投影体系由空间坐标系、投射方向和投影面三者决定，空间坐标系是确定的，于是，轴测投影体系将根据投射方向和投影面的不同选择决定，这样得到的轴测投影体系可以有无限多个。

在长期的工程实践应用中只采用了少数几个轴测投影，由特殊的轴测参数轴间角∠1，∠2，∠3和轴向变形系数η，η，η给出(图6)[9-12]。

(1) 正等测。轴向变形系数η=η=η=0.816，轴间角∠1=∠2=∠3=120°。

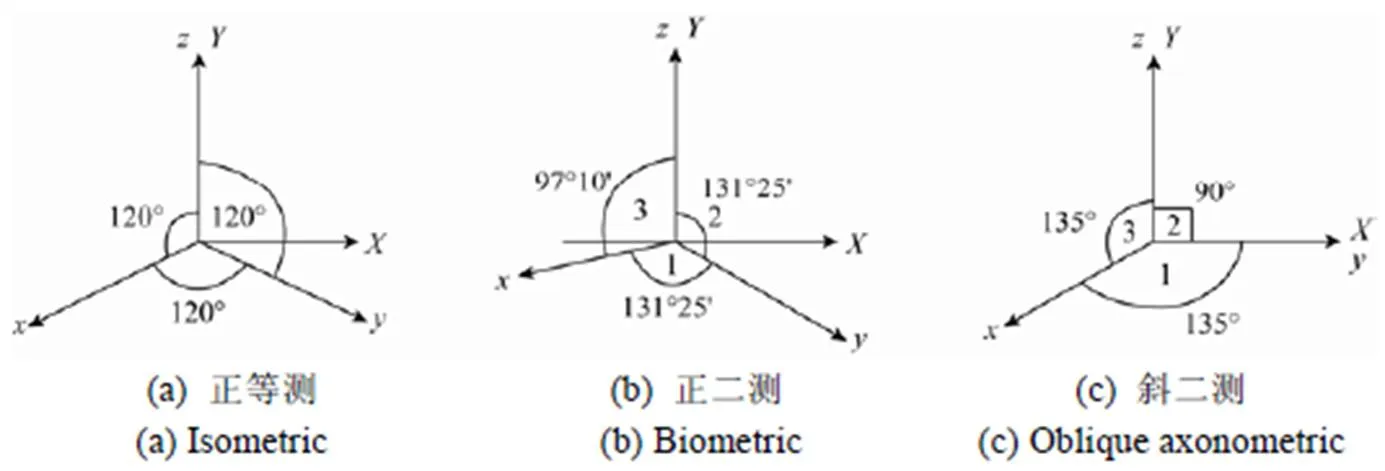
图6 常用轴测坐标系

(2) 正二测。取η=η=0.94，η=0.47，轴间角∠1=131°25'，∠2=131°25'，∠3=97°10'。

(3) 斜二测。取η=0.5，=η=1.0，轴间角∠1=135°，∠2=90°，∠3=135°。

轴测图并不是空间的精确描述，其功能是产生较好的空间视觉效果，可根据需要选用其中一种轴测图。上述轴向变形系数和轴间角是画法几何的经典值，并非有严格的标准，将轴向变形系数调整，只是将形体沿轴测方向等比扩大或缩小而已，只要视觉上能够接受。

3.1 正轴测投影要素

参阅图1~2，，，为三投影轴，为投影平面，投射线1⊥，三投影轴与的交点分别为，，和1，1，1分别为空间坐标系在面上的投影。△1，△1和△1是共点的3个直角三角形。1=∠1，1=∠1，1=∠1为投射线1的方向角。

3.2 正轴测投影的基本关系式

根据轴测投影体系基本关系式(1)，由于=90°，所以，正轴测投影的基本关系式为式(9)和式(10)。

(1) 正轴测轴向变形系数与轴间角的关系。根据轴测投影定义，轴向变形系数η，η，η与轴间角∠1，∠2，∠3间的关系是确定的，即

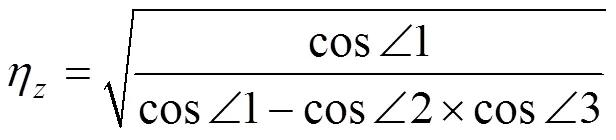
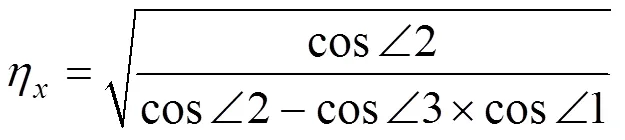
如果先给定轴向变形系数，可由式(11)~(13)求得轴间角；如先给定轴间角，则可由式(14)~(16)求得轴向变形系数。

(2) 正二测的轴向变形系数与轴间角

已知：根据画法几何的约定，一般正二测轴向变形系数取η=η=2η(图6(b))

求：轴间角。由式(7)解之得：

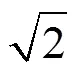
由式(11)~(13)，可解得

因为轴测图的作用主要是图示，是一种眼观标准，不严格体现在几何形体的尺寸量度上，因此对轴向系数并未有严格的精确要求。实际绘制时，一般教材均建议对正等测和正二测的轴向系数靠向简单的比例因子，例如0.47取0.50，0.94取1.00等等。

3.3 斜轴测投影要素

(1) 斜轴测投影的基本关系式。斜轴测投影时(图3~4)，平行投影的方向是不平行于投影面法线方向的，设其与投影面△成角，斜轴测投影轴为1，1和1，坐标原点在投影面△上的正投影是*前已证明，斜轴测投影时有

η2+η2+η2=1+1/sin2=2+cot2

这是斜轴测投影的基本关系式，即投影方向与变形系数之间的关系。斜轴测投影的变形系数的平方和随投射线对轴测投影面的夹角而变化。

(2) 空间参数与轴测参数间的关系。在斜轴测投影中，还有以下结论：笛卡尔坐标轴(空间参数)与对应的轴测投影轴(轴测参数)的放射比(轴向变形系数)和两者的夹角余弦的乘积之和等于2，即有

ηcos+ηcos+ηcos=2

但与正轴测投影不同，在斜轴测投影中，下列3式不成立，即

cos=η，cos=η，cos=η

但是有

η(cos–η)+η(cos–η)+η(cos–η)=–ctg2

此式给出了笛卡尔坐标轴在任意轴测投影面上作轴测投影时，坐标轴与轴测轴两者仿射比(变形系数)之间的关系，以及斜投射方向与投影面法向的夹角之间的关系。

4 投影面和轴测轴的求取

决定一个轴测投影的要素是投影面，以及投影方向。

(1) 投影面。轴测图在投影面上得到，与投射方向的选择相关。

方式1. 可以是形体不动，改变投影面。这常是一种斜投影方式。

方式2.固定投影面，对形体作空间变换。这常是一种正投影方式。

方式1多用于理论研究，方式2多用于实际应用，工程制图中常用坐标平面作为投影面。

(2) 投射方向。在投影面决定以后，投射方向决定正投影(投射方向与投影面垂直)还是斜投影(投射方向倾斜于投影面)。

(3) 坐标轴。空间是笛卡尔坐标系，投影面上是轴测坐标系，后者是前者在投影面上的投影。

4.1 固定形体寻找投影面产生轴测图

先讨论固定形体，形体在这样的局部坐标系下表示：其至少有一个主面平行于坐标平面。在空间坐标系下决定一个投影面，给出的一个表达形式：面上的一个点，和在空间坐标系下的单位法向量，使得形体在面上的投影是形体的轴测图。

(1) 正等测图投影面的决定。轴测投影初始是得到正等测投影，投影面的法向与空间坐标系 3个坐标轴有相同的夹角，所以在空间坐标系的单位法向是：(0.577350, 0.577350, 0.577350)。

面上一点的选择可有无穷多种，可以在空间坐标系的，，3个轴上，离原点距离相等的3个点0，1，2构筑一个等边三角形，通过该3点构筑的平面作为形体的投影面，其法向满足正等测投影面的法向条件(图7~9中的灰色面)。例如：可取以下3个点：0(0.0, 0.0, 1.0)，1(1.0, 0.0, 0.0)，2(0.0, 1.0, 0.0)。根据显示要求， 3个点0，1，2可以按同比例改变，保证单位法向不变。

面投影中心为，有以下的结论(参阅图1~2)：

⊥，∠0=∠1=∠2=90°；

0，1，2在面上的投影分别为0，1和2；

0，1和2构成轴测坐标系。其3个轴间角相等，即

∠=∠=∠=∠01=∠02= ∠12=120°。

0：0=1：1=2：2=0.816。

形体在面上的投影。是在面上的正投影，表示的正等测图。相对于空间坐标系，投射方向是斜的(的单位法向是，图7)。

1+3组投射线各组各自互相平行，其中3组分别垂直于总坐标平面，1组垂直于面(平行于面的法向)，与3个坐标平面有相同的夹角。

形体的正轴测投影的线性尺寸与形体的线性尺寸比为0.816(=︰)，这个比例就是轴向变形系数。

图7~9是分别在正二测和正等测(注意两者重合)下显示的投影原理图。

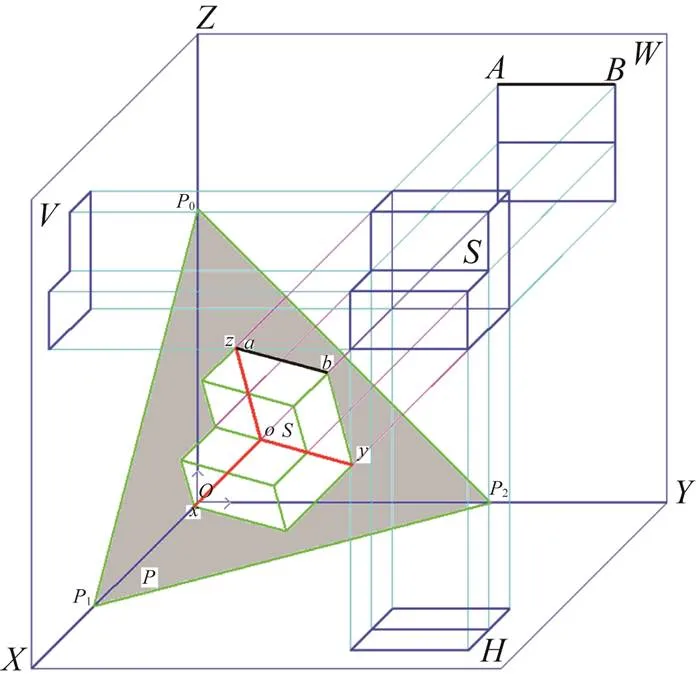
图7 正等测原理图

图8 正等测原理图之二

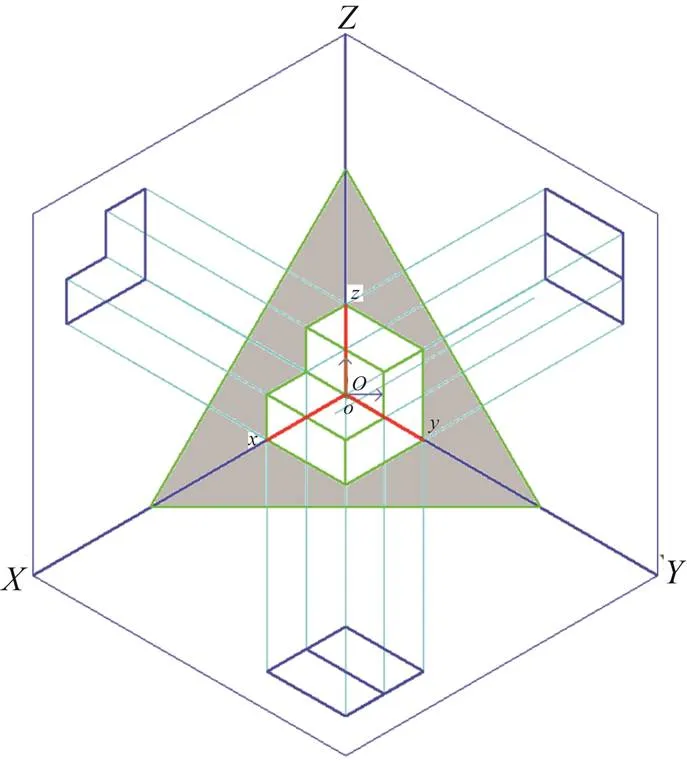
图9 正等测原理图之三

(2) 正二测图投影面的决定。正二测投影面(图10~12中的灰色面)，可在空间坐标系的，，3个轴上的3个点0，1，2构筑一个三角形，通过该3点构筑的平面作为形体的投影面。与正等测不同的是，3个点0，1，2离原点距离是不等的，三角形也不是等边三角形。

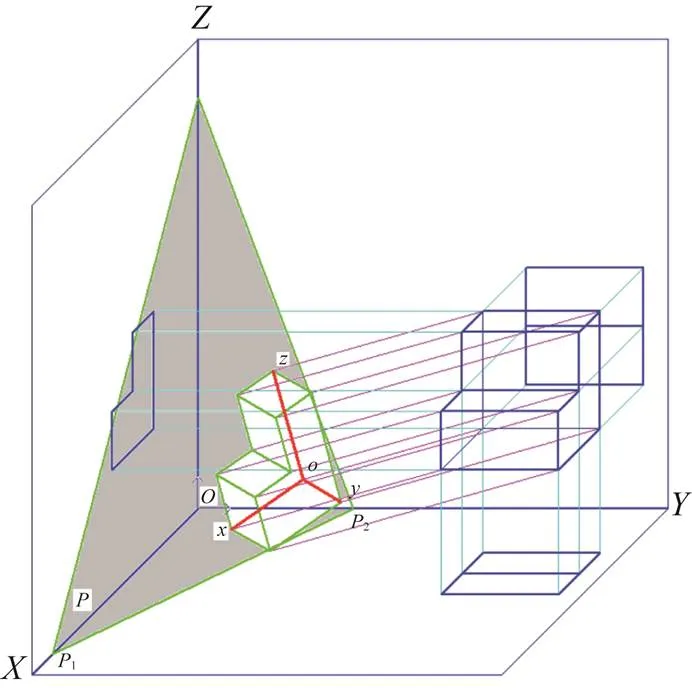
图10 正二测原理图

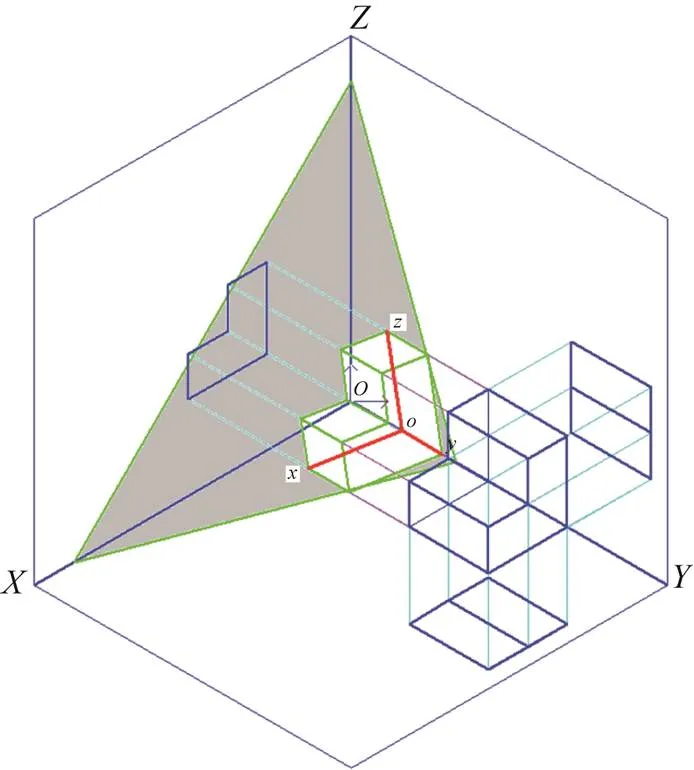
图11 正二测原理图之二

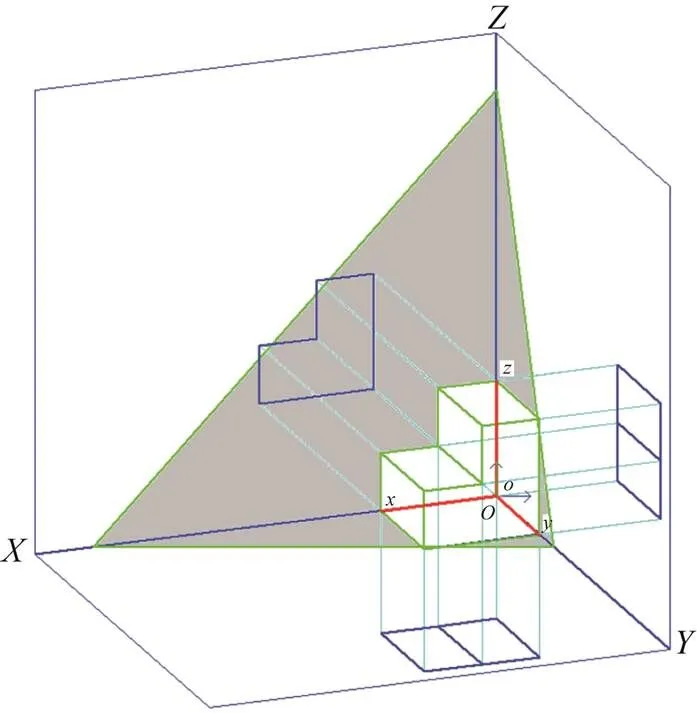
图12 正二测原理图之三

正二测投影面在空间坐标系的，，下的单位法向是：(0.881931, 0.333333, 0.333297)。

下面是一组构成投影面3点的例子，为方便，这3点可取在原坐标轴的轴上。其中，第一个可先决定，任选，后面两点根据选定的首点及正二测投影面的单位法向经计算得到：

1(0.0, 0.0, 1.0)，2(0.377918, 0.0, 0.0)，3(0.0, 0.999892, 0.0)

根据显示要求，1点可以离原点远一点，例如，取1(0.0, 0.0, 2.0)，1(0.0, 0.0, 3.0)等，2和3由正二测投影面的单位法向重新计算得到。

(3) 斜二测图投影面的决定。一般的叙述。斜二测图中，形体有一个主平面与投影面平行，投射线的方向是垂直于这个投影面的。所以，可以选择与面垂直的面作为斜二测图的投影面，投影面的法向与面平行。构筑一个以面法向作为新的轴，面作为新的平面的新坐标系，在这个新坐标系向经错切变换后向平面投影，这个投影就是形体的斜二测投影图。

但是，因为需要“形体有一个主平面与投影面平行”这样一个条件，而这个条件在选择形体坐标系时更为需要，所以，在斜二测图产生中，不建议选择除了坐标平面外的投影面。例如，选择的投影面是平面，那么，投射线的法向是：

(0.0, 0.0, 1.0)。

4.2 固定投影面而变换形体产生轴测图

这是产生轴测变换的另一种方式：通过对空间形体的旋转或者错切变换，将轴测投影转化为正投影。方法如下(图13~15)。

(1) 正等测图。如果以平面作为投影面，在这个面上产生正等测图。那么可先将空间形体绕轴旋转–45°，再绕轴正旋转35.26442° (35°15.865')然后向-平面投影(取,坐标)，得到正等测图。

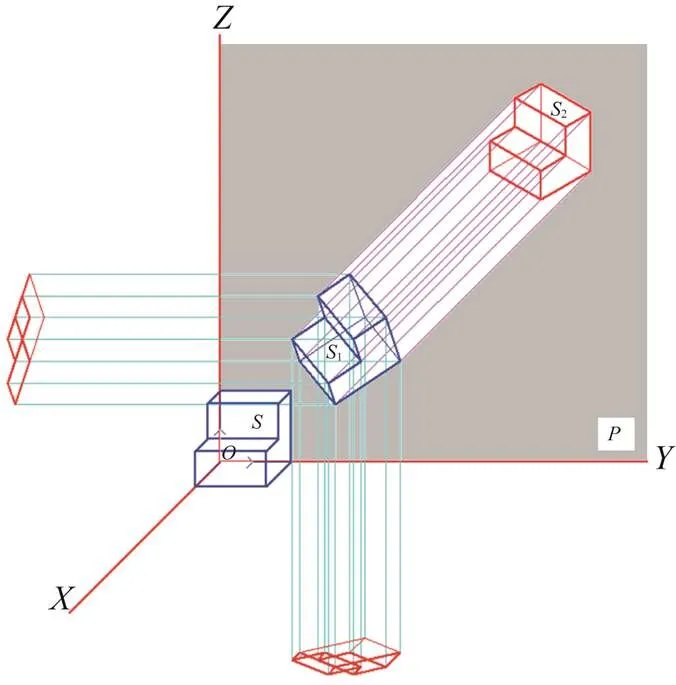
图13 旋转产生正等测图

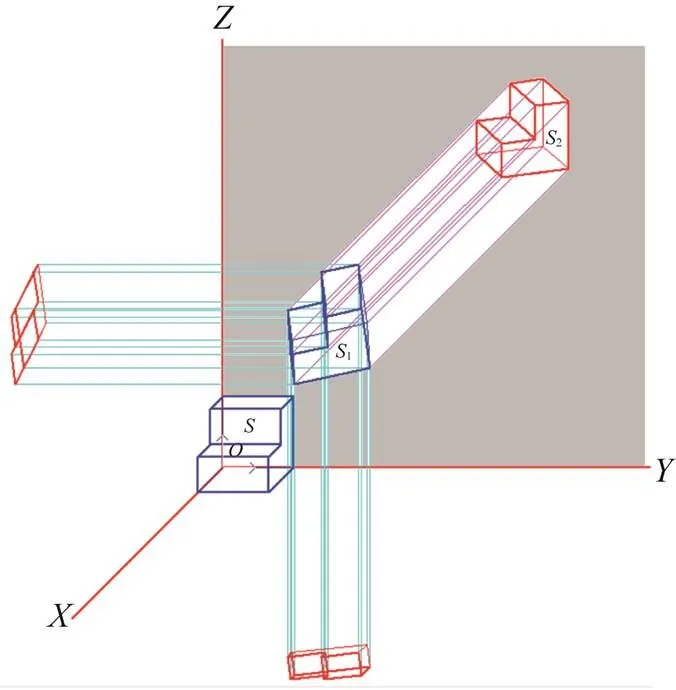
图14 旋转产生正二测图

图15 错切产生斜二测图

(2) 正二测图。如果将空间形体绕轴旋转–69.297539° (–69°17'10'')，再绕轴正旋转19.47122° (19°28'16'')，然后向平面投影(取,坐标)，得到正二测图。

(3) 斜二测图。先沿向错移–0.3535且离开轴([3,0]=–0.3535)，然后沿轴错移–0.3535且离开轴([3,1]=–0.3535)，然后向平面投影(取,坐标)，得到斜二测图。

下面是根据上述方法绘制的原理图，说明 如下：

：原始形体。

1：经过旋转或者错切变换后的一个三维“中间体” (因显示原因而作了平移)。

2：1在投影面面上的正投影2表示出的轴测图。

这里的面是与其中一个坐标平面重合的(图13~15)。1在其他2个坐标面上的投影标明，其与不是一个物体，只是借用其得到了轴测图罢了。实际上，1也是不存在的，只是计算中的一个过程而已，借用1在坐标平面上的正投影得到原始形体的轴测图。

5 总 结

空间视角的基本要素是能同时看到物体的3个可见面，因此用单面投影图表达一个形体的空间感觉，就要同时表述一个立方体的3个方向，即互相垂直的3个面，这才能接近于人们的视觉习惯，表达出立体感。三视图用3个视图分别表示形体的3个方向(面)，轴测图用一个视图同时表示三直三面角，其目标都是要表达形体的3个面。

本文重新审视了轴测投影的表述问题。认 为，轴测投影法是用平行投影的方法，沿投射方向将空间坐标系投射到投影面上得到轴测坐标系，在这个坐标系下表述空间形体，得到的图纸叫轴测图。

讨论了形体、投射线和投影平面等轴测投影的基本要素，和轴测投影的空间参数、轴测参数之间的关系，给出了其原理图和轴测图的2种生成方法。

轴测投影的理论是从坐标系及坐标轴的投影引入的，轴测投影体系中形体、投射方向和投影面之间的关系以及参数约束似乎也依赖于坐标系。但是，从几何的不变性，形体以及在平面上表述形体的正视图、轴测图等并不依赖于坐标系。

[1] 中国图学学会. 2012-2013图学学科发展报告[M]. 北京: 中国科学技术出版社, 2014: 3-30. China Graphics Society. Report on advances in graphics 2012-2013[M]. Beijing: Science and Technology of China Press, 2014: 3-30 (in Chinese).

[2] 何援军. 画法几何新解[J]. 图学学报, 2018, 39(1): 136-147. HE Y J. Interpretation of descriptive geometry[J]. Journal of Graphics, 2018, 39(1): 136-147 (in Chinese).

[3] 何援军. 图学与几何[J]. 图学学报, 2016, 37(6): 741-753. HE Y J. Graphics and gemetry[J]. Journal of Graphics, 2016, 37(6): 741-753 (in Chinese).

[4] 何援军, 王子茹. 谈谈图学教材[J]. 图学学报, 2015, 36(6): 819-827. HE Y J, WANG Z R. On graphics textbook[J]. Journal of Graphics, 2015, 36(6): 819-827 (in Chinese).

[5] 何援军. 一种基于几何的形计算机制[J]. 图学学报, 2015, 36(3): 319-330. HE Y J. A shape computing mechanism based on geometry[J]. Journal of Graphics, 2015, 36(3): 319-330 (in Chinese).

[6] 何援军, 童秉枢, 丁宇明, 等. 图与图学[J]. 图学学报, 2013, 34(4): 1-10. HE Y J, TONG B S, DING Y M, et al. Graph and graphics[J]. Journal of Graphics, 2013, 34(4): 1-10 (in Chinese).

[7] 于海燕, 蔡鸿明, 何援军. 图学计算基础[J]. 图学学报, 2013, 34(6): 1-5. YU H Y, CAI H M, HE Y J. The computational basis of graphics[J]. Journal of Graphics, 2013, 34(6): 1-5 (in Chinese).

[8] M∙ST∙包太兹, N∙P∙米列斯库. 轴测投影理论与应用[M].李世铨译. 北京:机械工业出版社, 1988: 158-166. BOTEZ M S T, MIRESCU N P. Mirescu editura tehnica[M]. LI S Q, Translation. Beijing: China Machine Press, 1988: 158-166 (in Chinese).

[9] 何援军. 几何计算[M]. 北京: 高等教育出版社, 2013: 1-26, 226-240. HE Y J. Gemetric computing[M]. Beijing: Higher Education Press, 2013: 1-26, 226-240 (in Chinese).

[10] 何援军. 计算机图形学[M]. 3版. 北京: 机械工业出版社, 2009: 180-183. HE Y J. Computer graphics[M]. 3rd ed. Beijing: China Machine Press, 2009: 180-183 (in Chinese).

[11] 何援军. 图形变换的几何化表示——论图形变换和投影的若干问题之一[J]. 计算机辅助设计与图形学学报, 2005, 17(4): 723-728. HE Y J. Geometric representation of graphics transformation[J]. Journal of Computer-Adied Design & Computer Graphics, 2005, 17(4): 723-728 (in Chinese).

[12] 何援军. 投影与任意轴测图的生成——论图形变换和投影的若干问题之二[J]. 计算机辅助设计与图形学学报, 2005, 17(4): 729-733. HE Y J. Projective transformation and generation of arbitrary axonometric drawing[J]. Journal of Computer-Adied Design & Computer Graphics, 2005, 17(4): 729-733 (in Chinese).

On axonometric projection

HE Yuan-jun

(Department of Computer Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The definition of axonometric projection was re-examined. Axonometric projection is a method by means of parallel projection, projecting the spatial coordinate system to the projection plane along the projection direction to obtain the axonometric coordinate system and express the spatial shape under this coordinate system. The resulting drawing is designated as axonometric drawing. Three views represent three directions of a body respectively, and the axonometric drawing represents three straight and three face angles with one view. The essence is to express the spatial body on the plane. This paper further discussed some fundamental problems in axonometric projection, such as the parallel projection system, axonometric triangle, axonometric projection system, the basic elements and formulas of axonometric projection, analyzed the similarities and differences between normal axonometric projection and oblique axonometric projection, and gave their schematic diagrams.

graphics; parallel projection system; axonometric projection; axonometric drawing

TP 391

10.11996/JG.j.2095-302X.2020040667

A

2095-302X(2020)04-0667-10

2020-02-16；

2020-05-21

21 May, 2020

16 February, 2020;

何援军(1945–)，男，浙江诸暨人，教授，博士生导师。主要研究领域为CAD/CG、几何计算的理论与算法研究等。E-mail：yjhe@sjtu.edu.cn

HE Yuan-jun(1945–), male, professor.His main research interests cover CAD/CG, theory and algorithm of geometric computing, etc. E-mail: yjhe@sjtu.edu.cn