数字化设计与制造三维MBD模型尺寸完备性检查及分析技术研究

张胜文，尤炎炎，李滨城，程德俊

数字化设计与制造三维MBD模型尺寸完备性检查及分析技术研究

张胜文1,2，尤炎炎1，李滨城1,2，程德俊1,2

(1. 江苏科技大学机械工程学院，江苏 镇江 212003；2. 江苏省船海机械装备先进制造重点实验室，江苏 镇江 212003)

针对三维基于模型的定义(MBD)技术存在的结构复杂、尺寸标注易出错、人工检查难度大等问题，提出了一种尺寸标注完备性检查及尺寸链分析技术。将空间标注尺寸转换成一系列的矩阵结构，从三维层面上保证模型中尺寸标注的完备性，并在此基础上分析计算尺寸链中各成员尺寸，验证设计尺寸的合理性。运用矩阵的数学形式表达、存储三维MBD模型上的标注尺寸，通过尺寸标注节点位置与数量关系判断尺寸冗余与缺失情况，并从模型上提取待判定尺寸链进行分析与校核，保证产品制造信息(PMI)传递的准确性并输出检查报告。以某型号船用柴油机的连杆为对象验证了该方法的可行性，极大降低了检查时间和设计错误率，提高了工作人员的设计效率。

三维MBD模型；产品制造信息；尺寸标注；完备性检查；尺寸链分析

随着计算机技术在制造业中的快速发展和数字化工厂的逐步推进，设计、工艺等过程逐步向无纸化转变，零部件从设计到制造过程的信息依据由传统的二维工程图纸转变为三维模型，三维模型在设计、工艺、生产等部门的应用成为必然趋势。产品制造信息(product manufacturing information，PMI)也由二维标注向三维标注的数字化模型发展，基于模型的定义(model based definition，MBD)技术以全新的方式定义产品，改变传统信息授权模式，工程图纸与三维实体模型结合的制造方法将被淘汰[1]。三维标注是MBD技术和未来无纸化设计与生产的关键环节，而尺寸标注作为最基本、最重要的设计制造信息，一直是计算机辅助设计(computer aided design，CAD)、计算机辅助工艺规划(computer aided process planning，CAPP)领域的重要研究课题。

实际工程应用中，标注问题占绘图总量的40%~60%。三维模型设计及制造信息繁多且分散，具有视图表达多样性和尺寸标注灵活性等特点[2]，在零件或装配体较复杂的情况下，极易出错，不仅影响设计效率，还关系后续工艺设计、生产装配、质量检测等各阶段信息来源的可靠性，成为困扰研发人员和使用者的技术难题[3-6]。

为提高工作效率和尺寸标注准确率，国内外学者进行了大量研究，并取得了阶段性的研究成果。谭祯[7]运用图论原理解决了多视图的尺寸完备性问题，但该方法仅适用于二维工程图。文献[8-9]提出将尺寸完备性转换为几何基元的约束状态判定，但对复杂基元的约束还需进一步研究。PODGORELEC等[10]提出用几何约束求解法检查几何元素的过约束问题，但未有效解决尺寸缺失问题。

目前，针对三维模型的尺寸标注检查问题，仍缺乏完整有效的检查方法。在前人研究的基础上，本文运用计算机表达模型中尺寸大小及位置关系，通过尺寸节点的位置、数量关系及矩阵运算规则自动化判断冗余与缺失情况，在三维模型上提取与分析待判定封闭环所在尺寸链，极大缩短了检查时间，解决了现有方法效率低、原理复杂等问题。

1 三维尺寸标注转换模型

三维尺寸标注转换模型以模型视图为检查单位，将空间标注尺寸按规则划分于不同标注平面，被计算机记录为多个维矩阵，并将尺寸标注的位置和大小关系客观映射到对应矩阵上，如图1所示。以此简化利用计算机识别提取尺寸、判断尺寸位置关系问题的繁琐性，为实现自动化的尺寸标注完备性检查提供准确无误的数据源。

图1 尺寸标注转换模型

1.1 尺寸标注转换模型的构建

构建尺寸标注转换模型需对模型数据进行预处理，包括尺寸的遍历、获取和存储，按标注平面与标注角度分类获取并存储尺寸，将零件三维空间尺寸转换为位于不同模型视图标注平面上的尺寸。

尺寸标注转换模型结构如图2所示，标注平面作为树状结构中的节点，标注角度为其子节点，获取零部件尺寸标注值、尺寸标注节点和尺寸所属成员类型，形成层次化的零部件标注尺寸存储结构，直观化表达标注点、线、面间的关系。其中，尺寸标注节点指尺寸标注时引出线的起点，尺寸所属成员类型指尺寸在该尺寸链中作为组成环或封闭环。

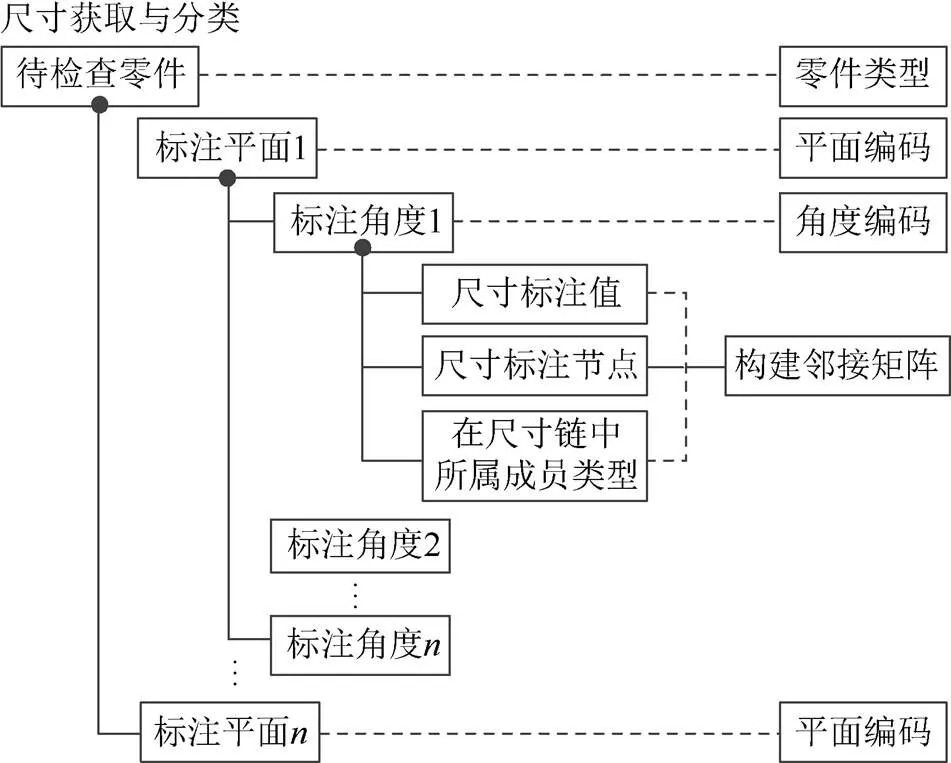
图2 尺寸标注转换模型结构

1.2 尺寸标注节点编码方法

尺寸标注节点的编码应无遗漏、无重复，确保涵盖模型上所有待查尺寸。

编码方法如图3所示，运用NX提供的相关函数遍历模型所有尺寸，按照标注平面与标注角度对各尺寸进行分类并获取对应标注节点，分级存储于容器中，如图4所示。由于不同标注尺寸间存在部分标注节点重合的问题，为保证标注节点编码的唯一对应关系，比较容器中各标注节点坐标位置，剔除重叠点，按照存储位置顺序由1至编码。

图3 各平面角度方向上尺寸标注节点编码

图4 尺寸标注节点分级存储方式

1.3 尺寸标注转换模型的数据存储结构

变换后的尺寸标注数据通过邻接矩阵将复杂的空间尺寸位置、大小关系转化为数学表达形式。矩阵中的各元素均与模型实际标注尺寸对应。

以阶矩阵为例，阶数为一标注平面某角度方向上标注尺寸的总节点数，矩阵元素a表示和节点间标注尺寸的数值大小。位于矩阵主对角线上元素下标=，没有实际表示意义，故设值为0。对称分布于主对角线两侧的元素a与a均表示和2个节点之间的尺寸数值，赋值相等，即

2 尺寸标注完备性检查

尺寸标注完备性检查即检查模型中标注尺寸是否能确定所有特征或所有对象(点、线、面等)的位置与大小，包括尺寸冗余及缺失。

尺寸标注信息的检查与分析过程如图5所示，导入模型后，对数据进行预处理，构建尺寸标注系统转换模型，获取建立邻接矩阵所需的各项信息，将标注尺寸用矩阵的数学方式表示；制定各类尺寸标注问题对应的检查规则，检查同一或不同标注平面间尺寸冗余与缺失情况；再根据反馈的检查结果修改尺寸标注，保证尺寸标注的正确与完整；然后提取显示待分析尺寸链，参考相关公式进行校核调整。

图5 尺寸标注信息检查与分析

2.1 尺寸冗余判断规则

尺寸冗余主要包括尺寸重复标注和尺寸标注多余形成封闭尺寸链2种情况。

2.1.1 尺寸重复标注判断

对于线性尺寸而言，每一尺寸均对应2个标注节点。若同一类型的多个尺寸(如水平、竖直、平行尺寸等)存在标注节点相同的情况，则尺寸间定存在重复标注。以此为据，判别尺寸重复标注的流程如图6所示，步骤如下：

步骤1. 对模型数据预处理，获取零部件尺寸集及各尺寸对应尺寸节点；

步骤2. 若尺寸节点数量大于1，则转到步骤3，否则循环到下一尺寸比较；

步骤3. 遍历零部件所有尺寸，将其与尺寸集中尺寸对比，若2个尺寸的标注节点对应的坐标位置相同，则转到步骤4，否则循环到下一尺寸比较；

步骤4.重复标注尺寸数加1，并在模型图上高亮显示重复标注的尺寸。

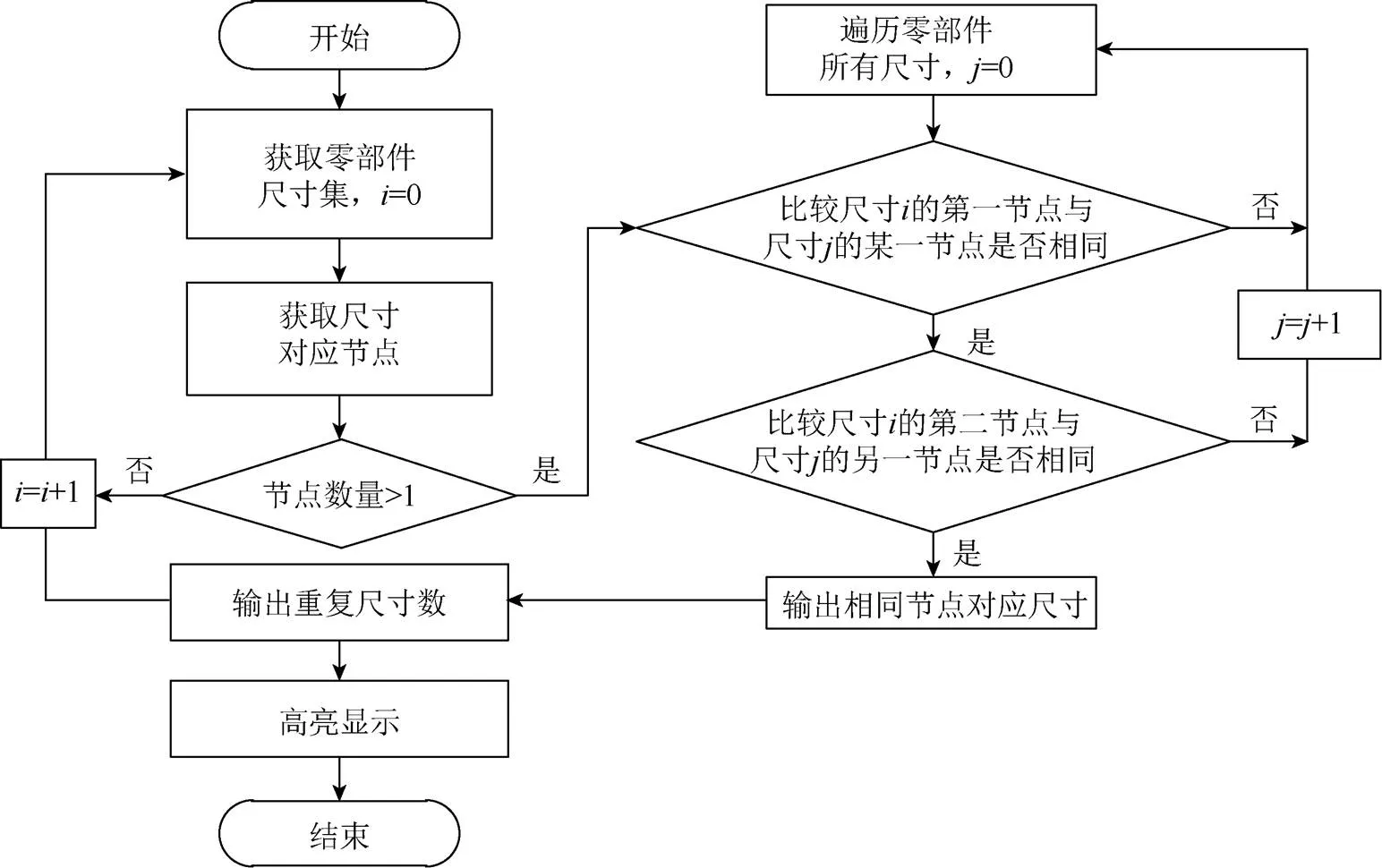
图6 重复标注判断

2.1.2 尺寸标注封闭性判断

由多个标注尺寸首尾相接形成的尺寸闭环，是造成尺寸冗余的主要原因。根据封闭尺寸链中各成员尺寸首尾相接的特性，提出了判别尺寸标注封闭性问题的具体方法。假设标注平面上有任一的标注尺寸为封闭环，以该尺寸的标注节点作为封闭环的始末元素，搜索与封闭环起点关联的尺寸环，标记该尺寸环的终止元素，并以此元素为新的搜索起点，以此循环，直到搜索出的尺寸环与封闭环的终止元素重合，呈现一条完整的封闭尺寸链。

同时，考虑到以同一封闭尺寸链中的不同尺寸元素作为封闭环而搜索到的尺寸链存在重复现象，待搜索结束后，利用计算机对各链中尺寸比较核对后，剔除多次重复获取的尺寸链。

2.2 尺寸缺失判断规则

尺寸缺失指现有标注无法完全约束点、线、面间的位置与大小关系，造成了尺寸标注不连通现象，包括已有标注节点间缺少必要的尺寸约束和节点未进行过标注但缺少必要的尺寸约束，如图7所示。

图7 尺寸缺失情况示意图

2.2.1 有尺寸标注节点的缺失

对某平面有个尺寸标注的节点而言，在不存在尺寸标注冗余的情况下，应有–1个尺寸对其完全约束，故尺寸缺失数目的判断如下

其中，为总标注尺寸数；为重复标注尺寸数；为封闭尺寸链数；为缺失尺寸数。

2.2.2 无尺寸标注节点的缺失

尺寸标注中存在点-线-面依次递进的约束关系，面的位置确定，则与面相关的线及点确定，故从模型中面的位置与大小是否完全确定的角度考虑无标注节点的缺失问题。针对机械零部件中常用平面、圆柱面、圆锥面、球面制定相应检查规则，检查孤立标注面的尺寸缺失情况，见表1。

表1 常用面的尺寸缺失检查规则

3 尺寸链分析与校核

在尺寸标注完备的基础上，为合理确定工序尺寸及公差、满足装配精度要求，必须快速、准确地提取表示各道工序和配合关系的尺寸链。利用计算机识别图形、描述位置关系来生成抽象的尺寸链图，具有一定难度，故本文提出一种在原模型上直接提取待判定封闭环所在尺寸链的方法，直观可视化显示尺寸链图，避免了上述存在的技术难题。

3.1 尺寸链分类

尺寸链是在零件加工或机器装配过程中，由相互关联的尺寸按顺序首尾相接排列而成的封闭尺寸组。按功能应用、几何特征、相互联系可作如图8所示分类。

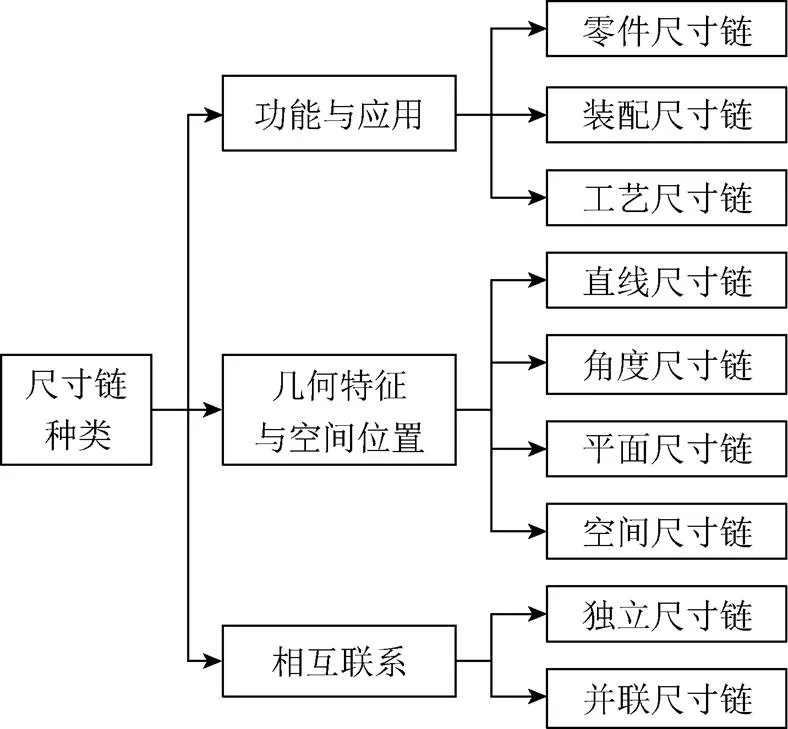
图8 尺寸链的种类

3.2 尺寸链提取方法

提取待判定尺寸链时，以尺寸标注节点为依据进行搜索，如图9所示。将封闭环的标注节点作为始末元素，搜索该环所在尺寸链的其他成员要素。当搜索到完整尺寸链时，在原三维模型图上高亮显示该链所有成员。对于尺寸链间的重叠嵌套现象，根据搜索路径可将其拆分成多个并联或串联尺寸链进行提取与计算。

图9 尺寸链提取

尺寸链提取原理与上述尺寸标注封闭性判断原理类似，但此处已知封闭环，可直接确定尺寸链搜索的起点与终点，省略了计算机比较各链中尺寸来剔除多次重复获取的尺寸链的过程。

3.3 增减环自动判断规则

增减环的判断是尺寸链校核计算的关键环节。若组成环的变化引起封闭环同向或反向变化，则该环为尺寸链的增环或减环。将尺寸链中各环当作矢量环，矢量方向由搜索起点指向终点元素，比较组成环与封闭环的矢量方向确定增减性，若矢量方向一致，则该环为增环；反之，则为减环。

以图10直线尺寸链为例，已知为封闭环，指定其节点2，3为搜索起点与终点，则搜索的尺寸顺序为---，节点顺序为2-1-4-3。封闭环矢量方向由起点2指向终点3，组成环的矢量方向与封闭环相同，故为增环；组成环，的矢量方向与封闭环相反，故为减环。

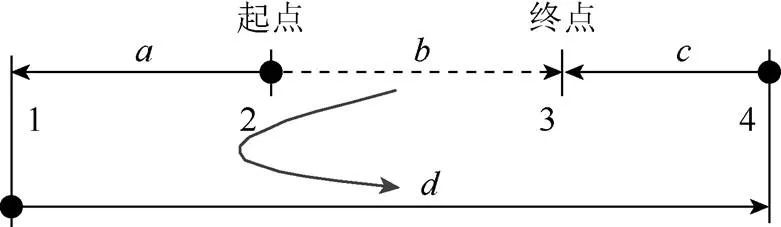
图10 组成环增减性判断示意图

3.4 校核计算

尺寸链校核计算即公差设计计算，是验证封闭环的基本尺寸和极限偏差是否满足设计要求的过程。采用极值法计算封闭环的上下偏差，验证封闭环设计值是否满足[0+0,0+0]范围。

4 应用与实例

以某型号船用柴油机的连杆为例，A-A面为其剖视图标注平面，该平面有3个标注角度，出现标注错误的是水平和竖直角度。首先，遍历该平面标注角度方向上的所有尺寸，建立树状存储结构，获取标注尺寸数和节点数。根据上述判断规则检查各种错误形式的数量，用绿、蓝、橙3色显示重复、封闭和缺失3种错误尺寸(图11)，并导出检查报告，如图12所示。图11中，尺寸1 110为重复标注尺寸，其所在尺寸链标注节点为4，由于–(+)<–1 (即4–(1+0)<3–1)，故判断尺寸缺失数为1，图11示虚线尺寸160或950为推荐缺失尺寸；尺寸165，107，29形成首尾相接的尺寸链，故封闭尺寸链数为1。尺寸标注完备性检查无误后，设定封闭环并提取其所在尺寸链，判断各组成环增减性，将各环数据代入校核计算公式验证设计合理性。

图11 尺寸完备性检查实例

图12 检查报告

5 结束语

本文归纳了尺寸标注存在的几种错误形式，并对不同错误的检查规则进行了具体说明，以三维模型标注尺寸为载体建立了尺寸存储结构及节点属性的树状图，为完备性检查与尺寸链计算提供数据源。针对图形与位置关系不易被计算机识别描述的问题，通过比较相邻尺寸间的节点位置关系，在原模型图上提取显示待判定尺寸链，无需计算机根据已有模型另外生成抽象的尺寸链图进行分析。根据上述原理以NX为平台开发了基于三维MBD模型的尺寸标注完备性检查及分析系统，并通过实验验证了方案的可行性和实用性，极大减少了检查时间和设计错误率。本文方法目前还无法应用于孔、倒角等非线性尺寸标注的完备性检查，为进一步提高尺寸标注完备性检查的自动化程度，还需开展针对非线性尺寸等检查方法方面的研究。

[1] 朱广涛. 基于三维模型的PMI信息提取及应用技术研究[D]. 廊坊: 北华航天工业学院, 2018. ZHU G T. Research on PMI information on extraction and application technology based on 3D model[D]. Langfang: North China Institute of Aerospace Engineering, 2018 (in Chinese).

[2] 纪杨建, 张树有, 谭建荣. 基于空间坐标转换模型的多视图尺寸完备性检查[J]. 计算机辅助设计与图形学学报, 2001, 13(6): 561-565. JI Y J, ZHANG S Y, TAN J R. Completeness testing of dimensioning in multi-views based on space coordinate transformation[J]. Journal of Computer-Aided Design & Computer Graphics, 2001, 13(6): 561-565 (in Chinese).

[3] 卢晓露. 基于特征建模的三维尺寸自动标注研究[D]. 武汉: 华中科技大学, 2019. LU X L. Research on automatic annotation of 3D dimensions based on feature modeling[D]. Wuhan: Huazhong University of Science and Technology, 2019 (in Chinese).

[4] 王永霞. 船用柴油机关键件全三维数字化定义及信息完备性检查技术研究[D]. 镇江: 江苏科技大学, 2017. WANG Y X. Research on full three dimensional digital definition and information integrity check technology of key components of marine diesel engine[D]. Zhenjiang: Jiangsu University of Science and Technology, 2017 (in Chinese).

[5] 刘晓军, 程亚龙, 邢嘉路, 等. 三维尺寸标注及完备性检测技术发展概况[J]. 机械制造与自动化, 2017, 46(2): 1-5, 20. LIU X J, CHENG Y L, XING J L, et al. Development of 3D dimensioning and completeness detection technology[J]. Machinery Manufacturing & Automation, 2017, 46(2): 1-5, 20 (in Chinese).

[6] 罗磊, 刘远, 郑国磊. 三维零件模型工程尺寸完备性检查算法[J]. 计算机辅助设计与图形学学报, 2018, 30(9): 1748-1754. LUO L, LIU Y, ZHENG G L. Algorithm for checking the dimensional completion of 3D part model Engineering[J]. Journal of Computer-Aided Design & Computer Graphics, 2018, 30(9): 1748-1754 (in Chinese).

[7] 谭祯. 二维工程图尺寸完备性检查的研究[D]. 沈阳: 东北大学, 2008. TAN Z. Study on completeness testing of dimensioning in 2D drawing[D]. Shenyang: Northeastern University, 2008 (in Chinese).

[8] 程亚龙, 刘晓军, 刘金锋. 基于轨迹相交的三维顺序尺寸标注完备性检查[J]. 计算机集成制造系统, 2014, 20(8): 1799-1806. CHENG Y L, LIU X J, LIU J F. Completeness check of 3D sequential dimensioning based on trajectory intersection[J]. Computer Integrated Manufacturing System, 2014, 20(8): 1799-1806 (in Chinese).

[9] 付超凡. 基于MBD的三维尺寸完备性检查技术研究及实现[D]. 武汉: 华中科技大学, 2019. FU C F. Research and implementation of 3D dimensional completeness inspection technology based on MBD[D]. Wuhan: Huazhong University of Science and Technology, 2019 (in Chinese).

[10] PODGORELEC D, ŽALIK B, DOMITER V. Dealing with redundancy and inconsistency in constructive geometric constraint solving[J]. Advances in Engineering Software, 2007, 39(9): 770-786.

Dimensional completeness check and analytical technology of 3D MBD model

ZHANG Sheng-wen1,2, YOU Yan-yan1, LI Bin-cheng1,2, CHENG De-jun1,2

(1.School of Mechanical Engineering, Jiangsu University of Science and Technology, Zhenjiang Jiangsu 212003, China; 2. Jiangsu Provincial Key Laboratory of Advanced Manufacturing of Machinery and Equipment, Zhenjiang Jiangsu 212003, China)

A technology for checking the completeness of dimensioning and analyzing the dimensional chain was proposed to solve problems, such as complicated structure of the 3D model based definition (MBD) model, error-prone dimensioning and the difficulty of manual check. The spatial dimensions were converted into a series of matrices to ensure the completeness of the dimensions at 3D level, based on which the sizes of each member of the dimensional chain were calculated to verify the rationality of the design. Matrix was used to express and store the dimensions on the 3D model and the redundancy and deletion of the dimensions was judged by the position and quantity of dimension nodes. Then the to-be-judged dimensional chain was extracted from the model for analysis and verification to ensure the accuracy of product manufacturing information transmission and an inspection report was produced. The feasibility of the method was verified by using the connecting rod of a certain type of marine diesel engine, which greatly reduced the inspection time and the design error rate and improved the design efficiency of the staff.

model-based 3D definition; product manufacturing information; dimensioning; completeness check; dimensional chain analysis

TP 391

10.11996/JG.j.2095-302X.2020040599

A

2095-302X(2020)04-0599-07

2020-01-30；

2020-03-02

2March, 2020

30 January, 2020；

国防基础科研基金(B0720060844)

National Defense Basic Scientific Research Foundation (B0720060844)

张胜文(1963-)，男，安徽阜阳人，教授，博士，硕士生导师。主要研究方向为CAD/CAPP/CAM集成技术、先进加工工艺与装备、数字制造系统等。E-mail：651565706@qq.com

ZHANG Sheng-wen (1963-), male, professor, Ph.D. His main research interests cover CAD/CAPP/CAM integration technology, advanced processing technology and equipment, digital manufacturing systems, etc. E-mail：651565706@qq.com