特大型城市具有需求流动性约束的急救中心设施选址优化

王伟 张佳玮 李明琨 赵霞

摘 要： 以我国特大型城市的急救设施布局为研究对象，探讨需求流动性约束下的设施点区位决策，决策过程充分考虑需求的阶段性变化、设施点的成本因素和急救点服务容量等多方面因素。为兼顾服务成本与服务效率的不同目标，提出一种两阶段决策方法，在第一阶段控制初期投入成本，同时在第二阶段通过合理的分配策略来提高服务急救点的效率。选取上海市中心城区急救点布局的真实案例，将两阶段模型应用于决策过程，获得的可行解决方案可有效提升城市管理者的决策水平与急救服务效率，在有效覆盖比率等指标上优于上海市政府规划的具体要求，高出近6个百分点。通过案例解读，验证了该方法是对选址问题理论方法模型的有效补充。

关键词： 特大型城市;流动性;急救中心;选址;两阶段优化

中图分类号： F 294.1   文献标志码： A

Abstract： We study the location problem for emergency services with periodical change of demands. We consider various factors in the decision making， e.g. time-dependent change of demands， costs and capacities of facilities. We aim at minimizing the costs as well as maximizing the efficiency of services， and therefore we propose a two-stage optimization method. In the first stage， we introduce an integer programming model to cover all demand nodes with minimal number of costs. In the second stage， we attempt to improve the service level by re-allocating demand nodes to facilities. We study a real case in Shanghai. Experimental results indicate that our method generates a satisfactory solution for the authority， as 98.3% demand nodes can be covered.

Key words： metropolitan; mobility; emergency site; location; two-stage optimization

1 問题描述与模型建立

本研究考虑特大型城市应急医疗急救服务设施区位问题，其具有以下一些特点：1）急救服务的公共服务产品属性要求在设置急救点时，必须将服务功能辐射至城市的所有需求点。2）作为公共物品，社会公益属性是首要考虑因素，但财政资源的约束必然影响到应急服务设施的建设与布局。3）急救设施的选址一旦确定，其布局将在很长一段时期内基本不变。对急救服务点进行规划时，往往首先考虑在现阶段条件下，设施如何布局能够使服务范围更大。而人口的迁入迁出、老龄化、流动性等都可能在不同阶段影响城市不同区域的服务需求，使原本比较合理的布局规划需要重新调整。如何增加急救服务点选址规划的柔性和鲁棒性是本研究的一个重要问题。因此，笔者根据案例问题实际背景，提出一种两阶段规划模型方法。

阶段一：满足城市各区域的基本急救服务需求，规划急救设施点选址，使得财政支出最少;

阶段二：提升城市急救服务水平，基于前阶段所得结果，对城市需求点与设施点进行重新匹配，使得在一个更高标准下的服务覆盖范围最大。

基于此方法思路，规划模型建立如下：

符号说明：

N：急救服务设施点集合，包括现有急救服务点与新增备选急救服务设施点;

N0：计划开始前，已存在的急救服务设施点集合，例如N0={j∈N|x0j=1}，其中x0j=1表示急救服务设施的初始状态为“被选中”;

M：需求点集合;

aij：0-1参数，当aij=1时，在Sar标准下，需求点i在急救服务设施点j的覆盖范围内;

bij：0-1参数，当bij=1时，在Sbr标准下，需求点i在急救服务设施点j的覆盖范围内;

fj：建设或移除急救服务设施点j的费用;

vj：维持急救服务设施点j运行的费用;

hi：在工作时间段内，需求点i的人口数;

h′i：在非工作时间段内，需求点i的人口数;

Cj：急救服务设施点j能提供的服务人口容量。

决策变量：

xj：0-1决策变量，当xj=1时，急救服务设施点j在候选集合中被选中;

yij：0-1决策变量，当yij=1时，表示在Sar标准下，需求点i指派给急救服务设施点j;

zij：0-1决策变量，当yij=1时，表示在Sbr标准下，需求点i分配给急救服务设施点j。

此阶段目标函数为在Sbr标准和需求流动性特征下，急救点能覆盖的加权总人口数最大。

（7）表示对任意需求点i，在Sbr标准下，最多只能被指派给一个急救点服务。

（8）表示对任意需求点i，如果能被指派给急救点j，急救点j必须被选中且在Sbr标准下可覆盖到需求点。

（9）和（10）表示在设施点已选定的前提下，对任意急救点j，不论何时间段，指派给急救点j的需求点人口之和不能超过其服务能力。

2 案例研究

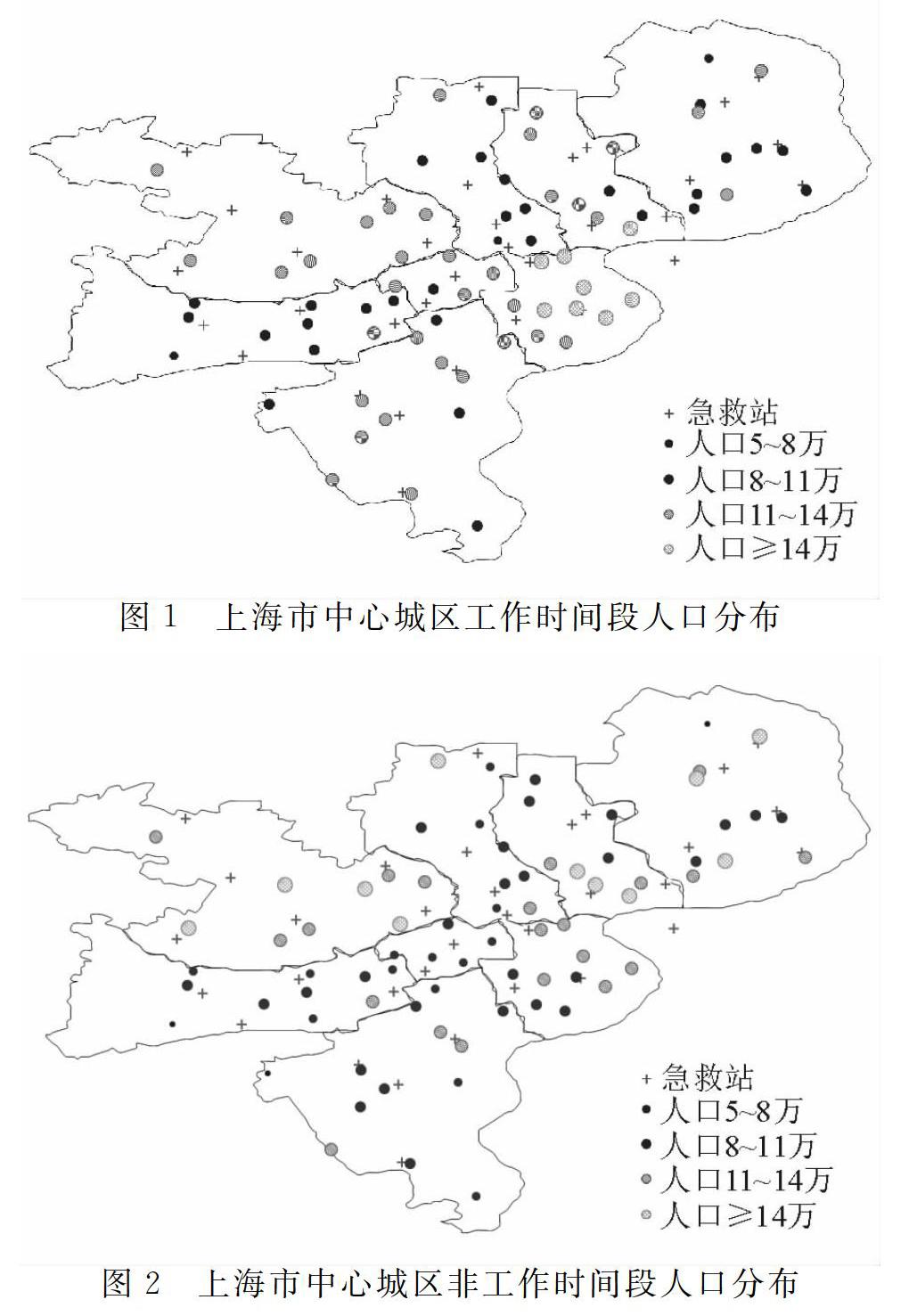
本文选取上海市的实际案例进行分析研究。随着城市的发展扩张，不同区域间的功能定位和规划各不相同，人口在区域间的流动性特征明显，并以工作时段与非工作时段的区域人口变化最为显著。本案例以2011年、2012年上海市各区县统计年鉴、上海市第六次人口普查全国人口普查中的统计资料等为依据，对上海中心城区8个区76个街道在工作时间段和非工作时间段的人口分布分别绘制图形，如图1所示。

从图1和图2可以明显看出上海中心城区的商业工作区和居民住宅区的人口周期性变化特征。需要说明的是，上海目前对中心城区与各郊区县的院前医疗急救服务采取财政独立、分开管理的方式。本文选取由上海市政府统一管理的中心城区进行进一步数据分析。

参数设定：

（1） 人口

根据前述统计资料，非工作时间段，中心城区人口数量以常住人口基准作为参考，设定为792.44万人。工作时间段，以上海各区县法人单位从业人员作为参考，设定为858.64万人。居民需求点的选择至中心城区街道这一层级，即以上海市中心城区76个街道两个时间段的人口情况为需求点的研究对象。以18～60岁上班族作为人口流动的主体，考察他们一天中处于两个不同时段的位置状态，忽略人们因短暂出行等导致的人口流动情况。

（2） 备选急救点集合

考虑到上海城市土地资源稀缺性、医疗资源分布不平衡、行政审批制度等客观因素，在上海已开设的医疗机构中，筛选出146家符合要求的医疗机构作为急救点选址的备选点集合。

（3） 服务覆盖半径

根据《上海市院前医疗急救事业发展“十二五”规划》，中心城区急救站的有效急救半径为3～5公里。因此，在第一阶段规划中，从社会公共服务属性出发，以公平性、全覆盖等为主要标准，将急救点的基础服务覆盖半径设定为5公里。在第二阶段，将急救点的服务覆盖半径设定为3公里，考察如何提升各急救点的服务效率。

（4） 急救站服务容量

根据已经建立并营运的33个（包括浦东1个）急救点、210辆救护车的部署量，以及《上海市院前医疗急救事业发展“十二五”规划》市民日常急救车辆保持≥0.25辆/万常住人口的水平要求，经测算，平均每个急救站的服务容量为25万常住人口。

（5） 建设成本

按照场所建设成本（或应急功能增建与改造成本）进行大致划定，具体成本参考：建设成本100万/个，假设移除成本为建设成本的10%，为10万/个，日常运作成本为25万/个。

（6） 时间权重

将人口的流动划分为工作时间段与非工作时间段，假定急救需求在一天中的任意时刻发生的概率相同。同時，上海等大城市居民在路途和工作上的时间约为总时间三分之一。因此，设定第二阶段模型中目标函数工作时间段的权重为1/3。

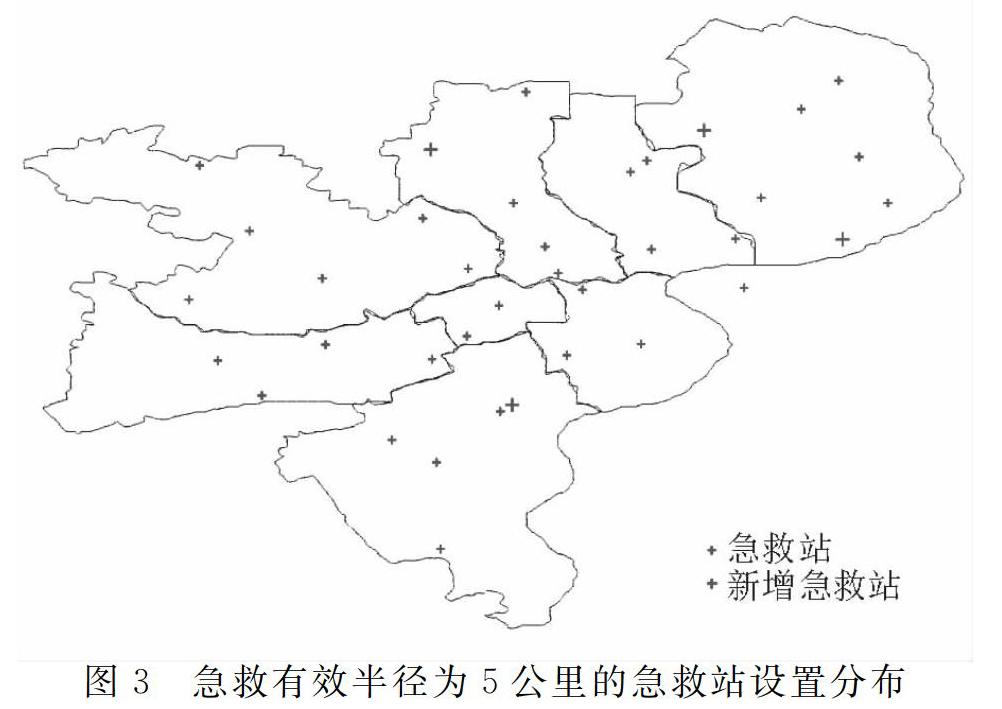
在3GHz处理器的台式机上使用IBM ILOG CPLEX 12.8测试所有案例数据。运行结果显示，在第一阶段，将保留原先已存在的33个急救点（标注为小十字），同时在146个备选点中选取了4个新的急救点（标注为大十字），即共需37个急救点，就能达成急救有效半径为5公里的全覆盖目标。规划后，急救点的分布状况与新增急救点的设置如图3所示。

在第二阶段规划中，考察急救服务有效半径为3公里时，如何最大化急救点的服务效率，使急救资源能够发挥最大的效用。鉴于资金、土地等资源的稀缺性约束，将上阶段所得到的急救点分布数据作为参数输入本阶段模型，并对急救设施的服务范围进行重新划分。结果显示，当对急救服务效率有更高要求时，部分需求点的服务不能及时响应。例如，以3公里为服务响应半径，通过调整需求点分配策略，可使绝大多数区域获得更好服务，但有两个需求点未能被覆盖，如图4所示。

为了更好体现两个阶段规划需求点与急救站点匹配结果的差异，将两阶段中决策变量和结果制表反映如下：

从表1可以看出，为了能在资源的有限性和服务的效率性上取得相对的平衡，在不同的决策阶段对急救点的服务策略进行调整，可在现有资源条件下，通过重新分配急救点的服务范围，来充分挖掘急救体系的整体潜能，从而提高急救系统的整体效率。

虽然第二阶段未能实现3公里半径的急救服务全覆盖（如表1中绿色空格部分），但是从已经被覆盖的期望人口数801万与整体期望人口数814万的比值看，在第二阶段提出的模型优化后所能完成的人口覆盖比率达到98.3%，比《上海市院前医疗急救事业发展“十二五”规划》要求的92.5%高出了近6个百分点。

与文献[28]的不同偏好模型的结果相比较，在成本控制优先考虑的情况下，当不能增加急救服务设施点时，急救服务响应水平和急救服务覆盖率与本文结果有显著差异。在3公里服务半径的高救援响应标准下，本文研究结果仍高于考虑有限预算偏好模型6.31个百分点。但预算设施点需增加4个，两模型急救点的分布状况与新增急救点的设置如图5所示。

考虑最大人口覆盖率方面，在较低急救响应标准（5公里服务半径）下，最大人口覆盖率模型与两阶段模型都能够达到100%人口覆盖率。但在同样新建四个急救站的情况下，本研究通过第二阶段再规划，使得在更高的急救响应标准（3公里服务半径）下，人口覆盖率仍可达98.3%。这对我国快速推进现代医疗急救服务，特别是上海等特大城市建设有重要意义。规划后，两模型急救点的分布状况与新增急救点的设置如图6所示。

3 结论

人口流动性已成为我国特大型城市的主要特征，并使得城市管理决策如急救设施布局的各种要素关系更加复杂。本文以上海这类特大型城市的急救设施布局为研究对象，探讨需求流动性约束下的设施点区位决策。在决策过程中，充分考虑了多方面的因素，如：需求的阶段性变化，设施点的成本因素和急救服务容量等。同时，为兼顾效率与效益，提出一种两阶段决策方法，在第一阶段控制初期投入成本，同时在第二阶段通过合理的分配策略来提高服务急救点的效率。

本研究选取上海市中心城区急救点布局的真实案例，将两阶段模型应用于布局决策优化过程。通过对案例数据的分析解读，验证方法模型的有效性。计算结果显示，采用本文提出方法获得的决策方案在有效覆盖比等指标上优于上海市政府规划的具体要求，同时可控制服务设施总体成本。因此，本模型方法可为城市管理者进行类似决策问题的有效理论方法工具。

本研究所探讨的具有需求流动性约束的急救中心区位布局问题，是对具有时间约束的覆盖问题的具体补充。研究显示，需求的流动性对急救点布局产生了巨大影響。本文提出两阶段模型方法，获得有效可行解，充实了文献中对此类问题的研究方法，并可作为后续扩展研究的基础。例如，可同时考虑人口覆盖率和成本预算的多目标优化模型，也可考虑居民急救需求水平的波动性与流动性的鲁棒优化模型，或者在更为详细数据资料的基础上，将两个时间段扩展为多个时间段，并可进一步考察不同急救点承担的服务压力的区别，探讨如何通过资源有效分配，平衡各急救点的服务压力等。

参考文献：

[1] 刘承良， 薛帅君. 上海市主城区公共服务设施网点分布的空间异质性[J]. 人文地理， 2019， 34（1）： 122-130.

[2] 陆相林，侯云先，林文，等.基于设施选址理论的小城镇应急医疗服务中心功能优化——以山东省滕州市为例[J]. 经济地理， 2011， 31（7）： 1119-1123.

[3] 齐腾飞，景军.中国1996—2015年城市院前急救反应时间分析[J].中国公共卫生，2017，33（10）：1466-1468.

[4] 施佳华，尹清菊，应仁祥，等.上海部分地区外来务工人员就医意愿、流向及影响因素分析[J].上海交通大学学报（医学版），2017，37（2）：234-239.

[5] TOREGAS C， SWAIN R， REVELLE C， et al. The location of emergency service facilities[J]. Operations Research， 1971， 19 （6）： 1363-1373.

[6] CHURCH R， REVELLE C. The maximal covering location problem[J]. Papers in Regional Science， 1974， 32 （1）： 101-118.

[7] INDRIASARI V， MAHMUD A R， AHMAD N， et al. Maximal service area problem for optimal siting of emergency facilities[J]. International Journal of Geographical Information Science， 2010， 24（2）： 213-230.

[8] GRIFFIN P M， SCHERRER C R， SWANN J L. Optimization of community health center locations and service offerings with statistical need estimation[J]. IIE Transactions， 2008，40（9）： 880-892.

[9] VERTER V， LAPIERRE S D. Location of preventive health care facilities[J]. Annals of Operations Research， 2002，110（1-4）： 123-132.

[10] SYDNEY C K， CHU CHU L. A modeling framework for hospital location and service allocation[J]. International Transactions in Operational Research， 2000，7（6）： 539-568.

[11] CURRENT J， OKELLY M. Locating emergency warning sirens[J]. Decision Sciences， 1992，23（1）： 221-234.

[12] HOGAN K， REVELLE C. Concept and applications of backup coverage[J]. Management Science， 1986（32）： 1434-1444.

[13] GENDREAU M， LAPORTE G， SEMET F. Solving an ambulance location model by tabu search[J]. Location Science， 1997，5（2）： 75-88.

[14] DOERNER K F， GUTJAHR W J， HARTL R F， et al. Heuristic solution of an extended double-coverage ambulance location problem for Austria[J]. Central European Journal of Operations Research， 2005，13（4）： 325-340.

[15] SCHMID V， DOERNER K F. Ambulance location and relocation problems with time-dependent travel times[J]. European Journal of Operational Research， 2010，207（3）： 1293-1303.

[16] 彭春，李金林，冉倫，等.需求不确定下应急医疗服务站鲁棒配置模型与算法[J].运筹与管理，2017，26（9）：21-28.

[17] REPEDE J F， J BERNARDO J. Developing and validating a decision support system for location emergency medical vehicles in Louisville， Kentucky[J]. European Journal of Operational Research， 1994，75（3）： 567-581.

[18] RAJAGOPALAN H， SAYDAM C. A minimum expected response model： formulation， heuristic solution， and application[J]. Socio-Economic Planning Sciences， 2009，43（4）： 253-262.

[19] ICHOUA S， GENDREAU M， POTVIN J Y. Vehicle dispatching with time-dependent travel times[J]. European Journal of Operational Research， 2003，144（2）： 379-396.

[20] FLEISCHMANN B， GIETZ M， GNUTZMANN S. Time-varying travel times in vehicle routing[J]. Transportation Science， 2004，38（2）： 160-173.

[21] FLEISCHMANN B， GNUTZMANN S， SANDVOSS E. Dynamic vehicle routing based on online traffic information[J]. Transportation Science， 2004，38（4）： 420-433.

[22] DONATI A V， MONTEMANNI R， CASAGRANDE R， et al. Time-dependent vehicle routing problem with a multi ant colony system[J]. European Journal of Operational Research， 2008，185（3）： 1174-1191.

[23] SCHMID V， DOERNER K F. Ambulance location and relocation problems with time-dependent travel times[J]. European Journal of Operational Research， 2010，207（3）： 1293-1303.

[24] 陈希，赵柳，张晓.考虑不确定性的医疗中心动态选址方法[J].工业工程与管理，2017，22（3）：93-98.

[25] 马云峰， 杨超， 张敏， 等. 基于时间满意的最大覆盖选址问题[J]. 中国管理科学， 2006， 14（2）： 45-51.

[26] 屈波， 杨超， 马云峰， 等. 基于时间满意的覆盖问题及混合遗传算法实现[J]. 工业工程与管理， 2008（1）：31-52.

[27] 翁克瑞. 面向快速响应与成本优化的设施选址问题[J]. 运筹与管理. 2012， 21（6）：32-37.

[28] REVELLE C， EISELT H A， DASKIN M S. A bibliography for some fundamental problem categories in discrete location science [J]. European Journal of Operational Research， 2008， 184（3）： 817-848.

[29] FARAHANI R Z， ASGARI N， HEIDARI N， et al. Covering problems in facility location： a review[J]. Computers & Industrial Engineering，2012， 62（1）： 368-407

[30] LI M K， ZHANG J W. Maximizing set coverage of emergency medical services with time-dependent restrictions： a case study in Shanghai[J]. HKIE Transactions， 2019， 26（1）： 9-19.