混合动力汽车工况识别及动态协调策略研究

吴静波，李明明，卢耀真，郭志军

(1.河南省汽车节能与新能源重点实验室，河南 洛阳 471000；2.河南科技大学车辆与交通工程学院，河南 洛阳 471000)

与传统燃油车相比，混合动力汽车拥有多种运行模式，如何合理地进行切换，实现节能减排，能量管理策略的制定是关键，而行驶工况是能量管理策略制定的基础，若能依据当前行驶工况的特点合理分配各个动力源的扭矩，可以进一步改善车辆的燃油经济性[1]。但是，车辆在道路上行驶时，实际工况是复杂多变的，因此，行驶工况的在线识别对能量管理策略的开发具有重大意义。

近些年，一些国内外学者在研究行驶工况的预测和判别时，主要采用模型预测的控制方法，预测汽车在未来时域内的扭矩需求，实时优化变量并得到扭矩分配比等参数。Borhan等[2]指出，混合动力汽车的需求扭矩在未来时域内将会按照指数函数的形式衰减，提出建立线性优化控制模型，然而，指数函数在预测车辆的动力需求时存在着很大的误差。Zhang等[3]建立了神经网络模型对驾驶员行为进行在线分类，并将驾驶员行为和预测的交通信息整合在一起优化目标函数，但是这些都需要大量的数据对神经网络进行训练，而且存在收敛速度慢等缺点。刘爽等[4]提出了一种基于驾驶意图识别的NAR神经网络短期工况预测方法，将模糊推理得到的驾驶意图与历史车速数据共同用于NAR神经网络短期工况预测。秦大同等[5]在应用欧几里得贴近度识别工况的基础上，运用粒子群算法优化不同工况下的汽车能量管理控制参数，但是常规的粒子群算法易陷入局部极值而出现早熟收敛，往往达不到全局最优。上述这些方法在进行工况预测时均未考虑在工况发生突变时产生的动态油耗等问题。

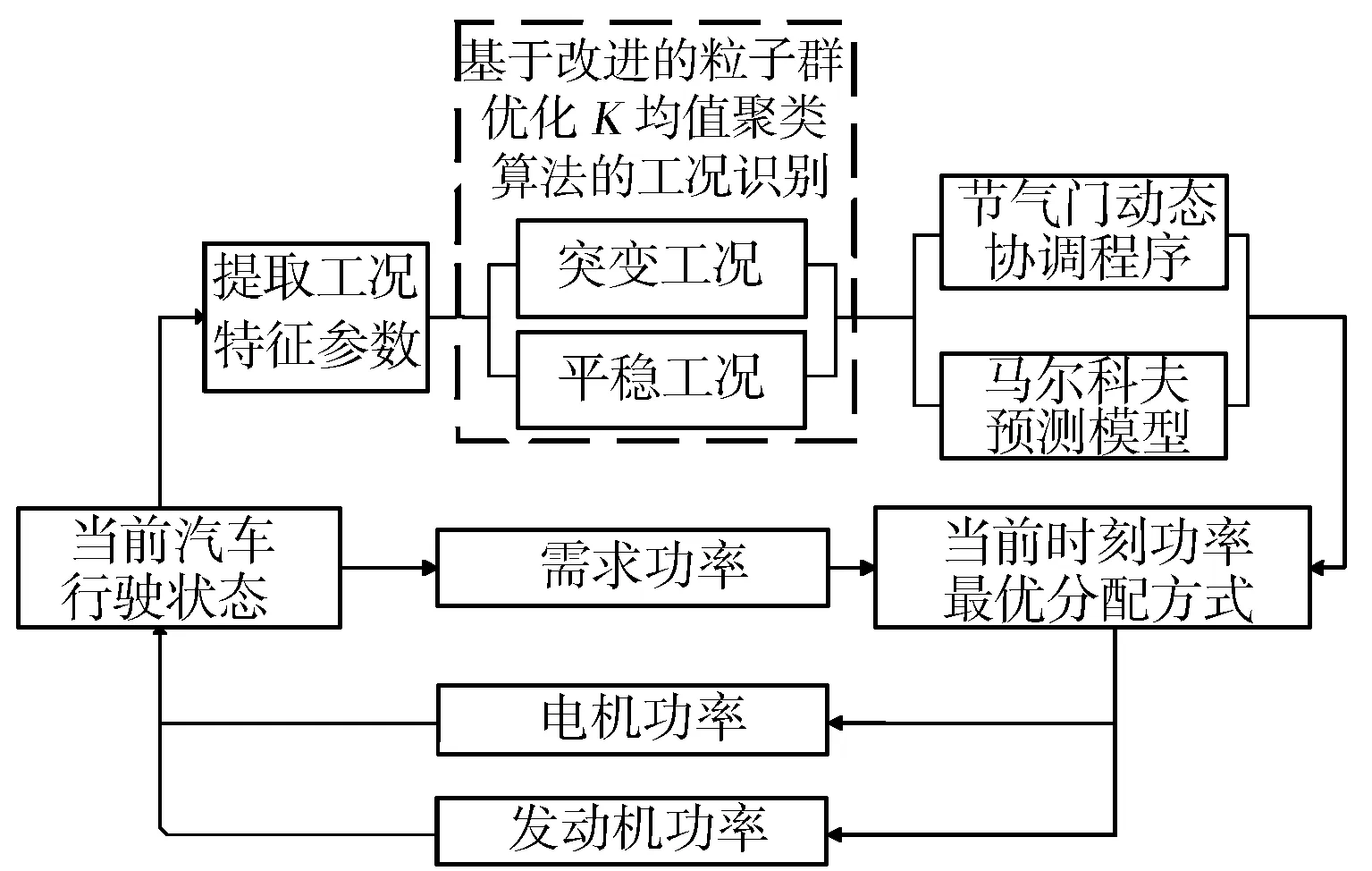
针对以上存在的问题，本研究在常规的粒子群算法基础之上进行改进，利用改进后的粒子群算法优化K均值聚类中心，之后进行工况分类[6]。针对不同的工况类型采用马尔科夫链或限制节气门开度变化率的方法对需求扭矩进行合理分配，并建立优化目标函数和约束条件，通过优化算法进行求解得到最优控制变量，从而降低混合动力汽车在工况突变时产生的动态油耗，改善行驶平顺性。

1 并联式混合动力系统模型

1.1 系统结构

本研究以BSG型混合动力汽车为研究对象，主要部件包括BSG(带传动一体化起动/发电机)、发动机、CVT变速器、动力电池等。BSG电机取代了传统的起动机,当其作为电动机时，动力电池放电提供助力；当其作为发电机时，动力电池处于充电状态，而且在启动时加入了电池自加热的功能，克服了在极端天气下启动困难等问题。系统结构见图1，整车主要部件参数见表1。

图1 BSG混合动力系统结构示意

表1 整车主要部件参数

1.2 混合动力汽车动力学模型

动力学模型为

0.5ρairCdAfvv2]，

(1)

ωL=vv/r，

(2)

ωe=ωLi0h，

(3)

(4)

式中：τL为车轮需求扭矩；vv为行驶速度；ρair为空气密度；R0为滚动阻力系数；α为坡度角；Cd为空气阻力系数；Af为迎风面积；mv为整车质量；g为重力加速度；ωL为车轮转速；r为车轮半径；h为换挡速比；ωe为发动机转速；τe为发动机扭矩；ηf为传动系统效率。

电机特性可描述为

Tm_min=fm_min(ωm)，

(5)

Tm_max=fm_max(ωm)，

(6)

Tm∈[Tm_min,Tm_max]，

(7)

ηm=fm_map(Tm,ωm)，

(8)

(9)

Ib=Pb/Vb。

(10)

式中：Tm_min，Tm_max分别为电机最小、最大扭矩；fm_min(ωm)为电机制动扭矩特性查表函数；fm_max(ωm)为电机驱动扭矩特性查表函数；ηm为电机效率；fm_map为电机效率函数；Ib为动力电池输出电流；Pb为输出功率；Vb为端电压。电机效率见图2。

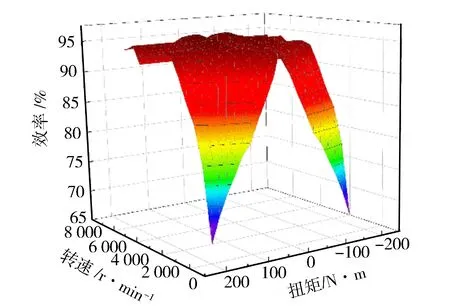
图2 电机效率Map图

2 工况在线识别

2.1 典型循环工况的构建

利用K均值聚类算法在离线状态下对工况进行划分，依据工况内的车速波动和节气门开度变化率，将行驶工况划分为平缓工况和突变工况。为了正确识别行驶工况的类型，需要谨慎提取工况特征参数。在综合考虑其他学者选择特征参数的基础之上，按照特征参数对工况识别的重要性，本研究选择了7个参数作为工况识别的特征参数[7]，分别为最高车速vmax、最低车速vmin、车速标准差vavg、最大加速度amax、最大减速度dmax、加速时间t、加速度标准方差ad。图3示出选取Cruise中25种工况构成的识别样本。

图3 综合后的基础工况

2.2 行驶工况的聚类

2.2.1改进粒子群优化K均值初始聚类中心

K均值算法的聚类中心选取时比较敏感，存在容易陷入局部最优解的缺陷。本研究将粒子群算法(PSO)与K均值聚类算法相结合，运用PSO算法的全局搜索能力对K-means算法的初始聚类中心进行优化，PSO算法具有在解空间中搜索的随机性特点，可以大大减小K-means算法陷入局部极值的概率，提高聚类结果的准确率[8]。

常规的PSO算法易陷入局部极值而出现早熟收敛的现象，因此本研究对各个粒子以及粒子群的最优值进行实时优化，对因陷入局部极值而出现早熟收敛的粒子进行变异，增加粒子群的多样性[9]，并采取以下公式更新粒子状态：

vid(t+1)=ωvid(t)+c1r1(pi-xid)+

c2r2(pg-xid)，

(11)

xid(t+1)=xid(t)+vid(t+1),

i=1,2,…n;d=1,2,…D。

(12)

式中：vid(t)，xid(t)为第t次迭代时粒子i的速度和位置；pi，pg为粒子i的个体最优位置和群体最优位置；ω为惯性权重系数；c1，c2为学习因子；r1，r2为随机权重。

pi可通过以下公式进行更新：

pi(t+1)=

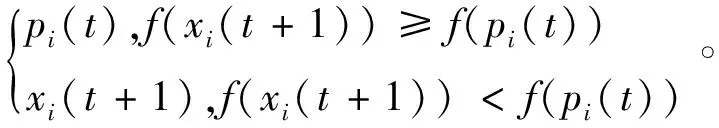
(13)

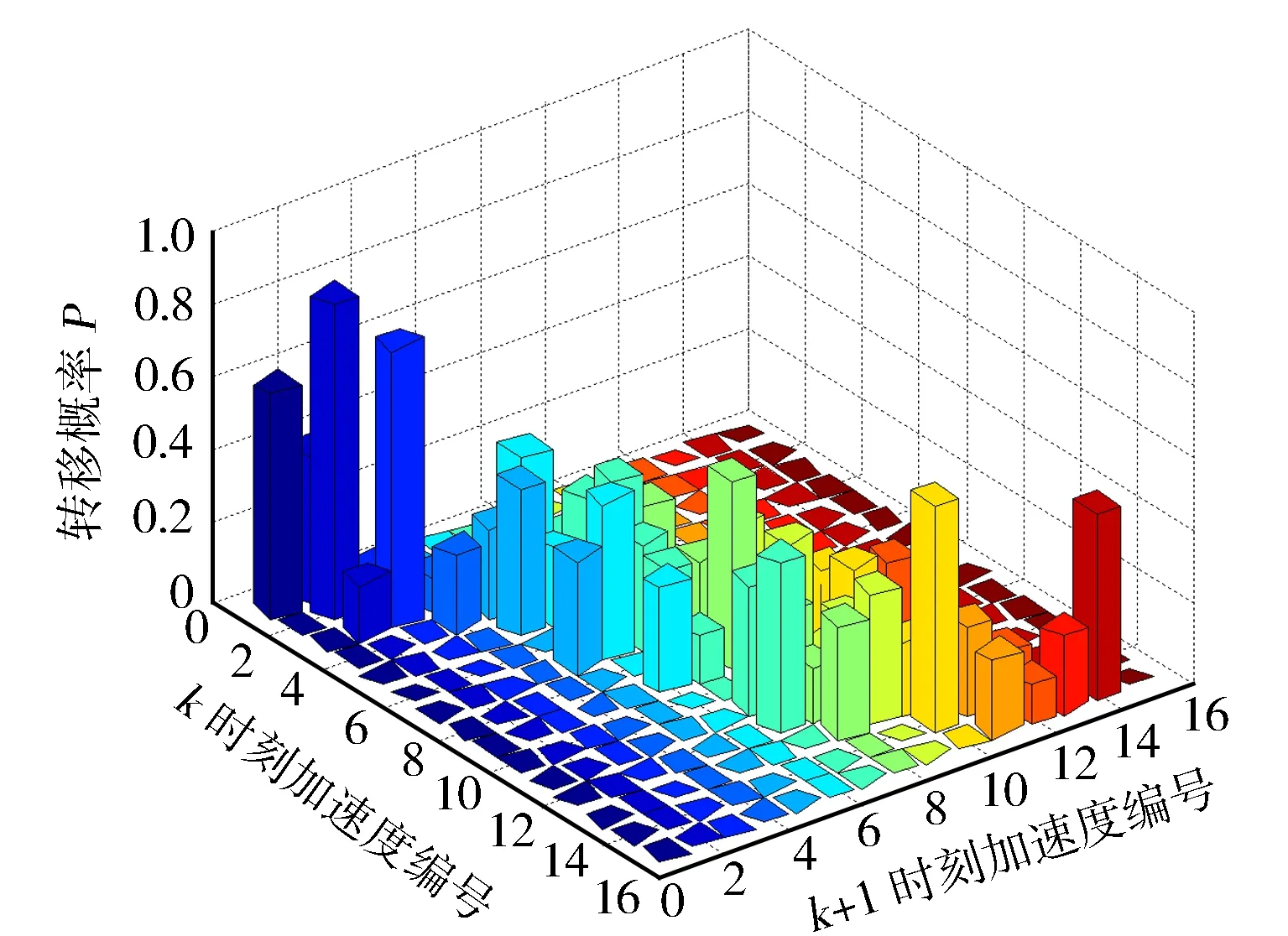
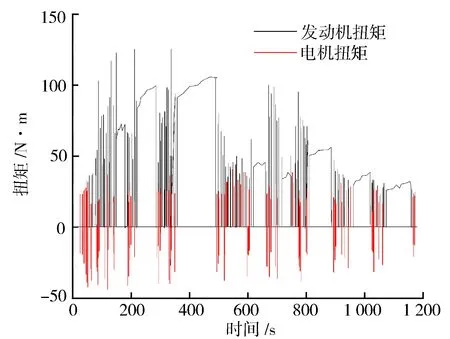
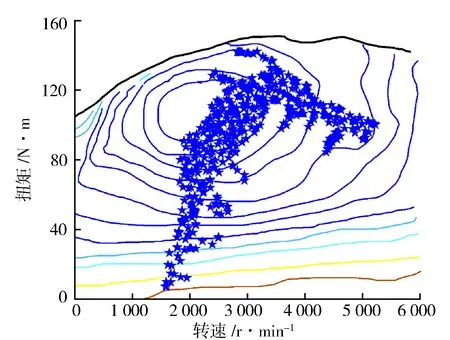
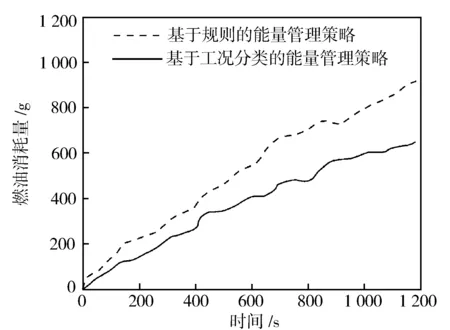
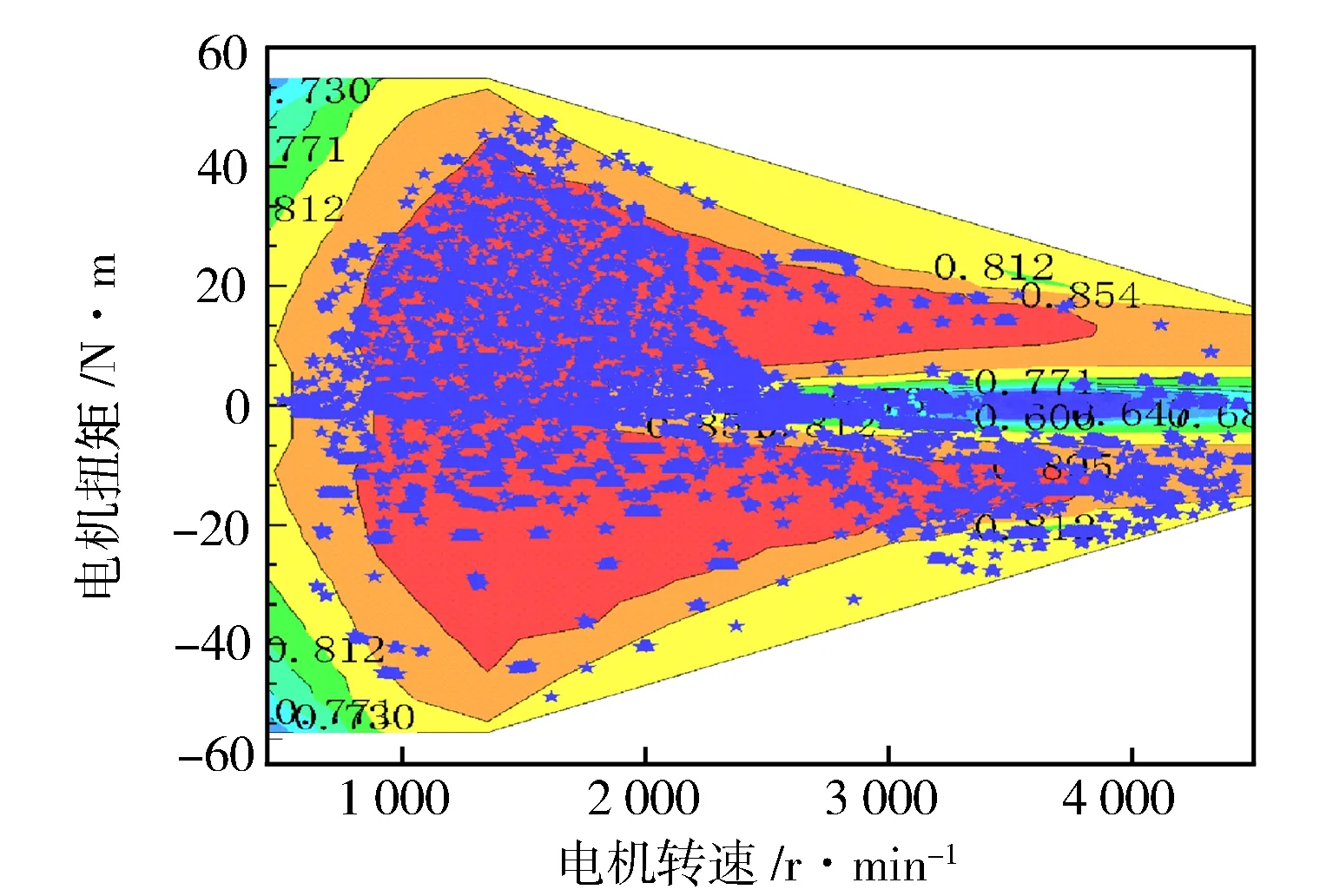
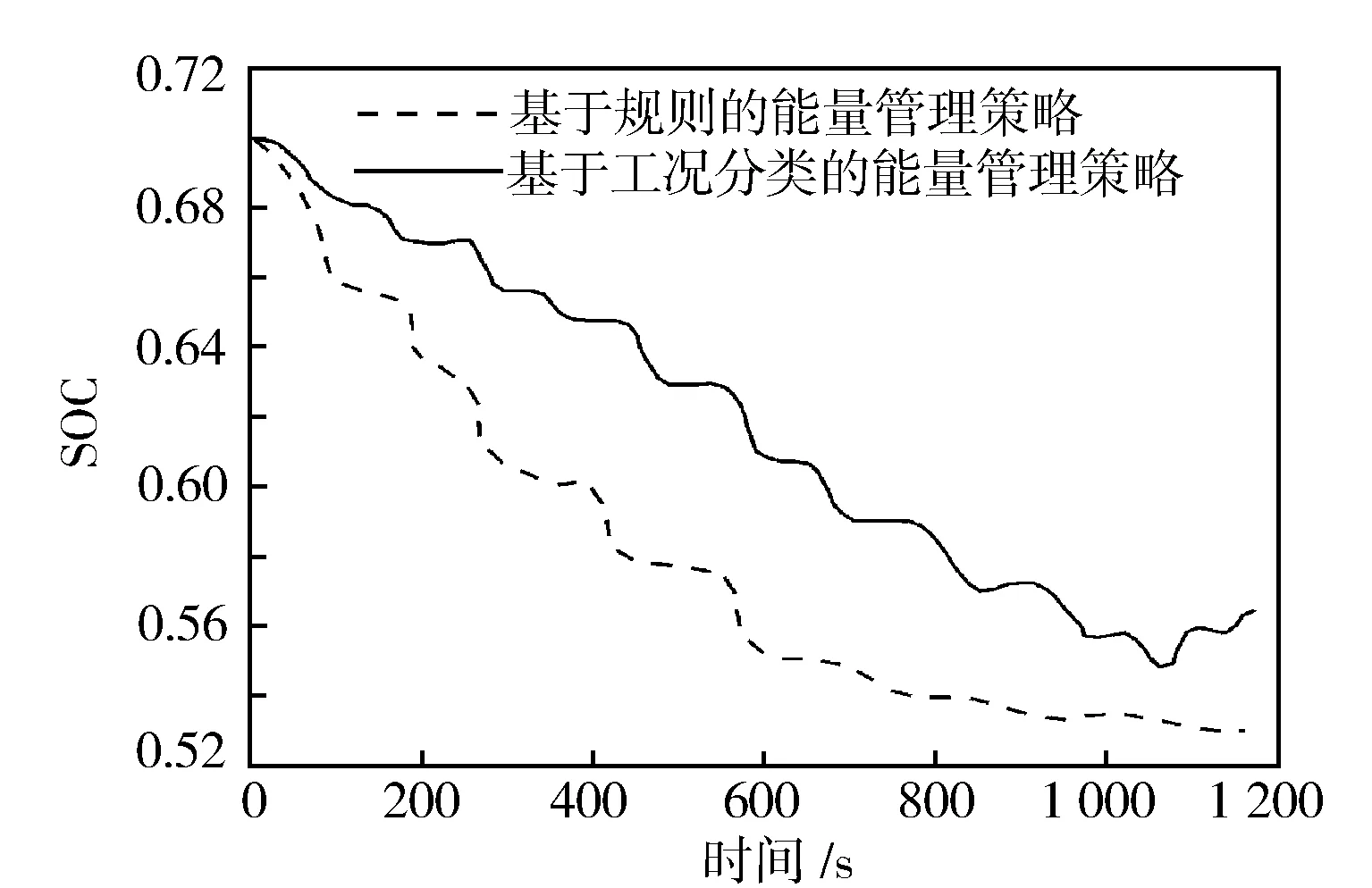
式中：f(x)为粒子群的适应度函数；f(xi(t+1))

2.2.2离线划分和在线识别

离线划分：

1)本研究进行工况判别的周期为120 s，判别结果每5 s更新一次，提取典型循环工况中每一采样时刻过去10 s的工况特征参数，将提取的特征参数作为一个数组[10]，得到样本数组[x11,x12,…x1m]，[x21,x22,…x2m]，…[xn1,xn2,…xnm]，其中m为特征参数数目，n为循环工况长度。

2)利用改进后的粒子群算法优化K均值算法的初始聚类中心，对待识别的工况数据进行聚类划分，得到最终的聚类中心c1=[c11,c12,…c1m],c2=[c21,c22,…c2m]，计算识别周期内待识别的工况数据到聚类中心的欧氏距离，并将数据按照就近原则分配到邻近的簇内。

3)根据聚类后得到的工况数据，计算聚类c1、聚类c2的类内差异w(C)、类间差异b(C)和准则函数E。

K均值算法的准则函数E为

(14)

类内差异w(C)为

(15)

类间差异b(C)为

(16)

不断调整聚类中心，直到准则函数E、w(C)、b(C)不再发生变动，则认为分类稳定，最终得到平缓工况的聚类中心c1和突变工况的聚类中心c2。

在线识别：

1)在混合动力汽车行驶过程中提取识别周期内随机工况的特征参数。

2)将提取的特征参数看作一个数组，根据下式计算该数组与各个最终聚类中心的欧氏距离。

(17)

3)将距离聚类中心c1或c2最近的一组工况数据视为该工况所属的簇，此簇中当前时刻的工况为该簇所代表的工况类型[9]。

2.3 平缓工况下的扭矩分配

平缓工况下，若能预知混合动力汽车在未来时域内的驾驶状态，便可以在当前时刻运用算法优化车辆在该时域内的驾驶状态。车辆的加速度在任一时刻只由当前的状态所决定，而与过去的状态无关，可认为车辆加速度的变化是一种马尔科夫过程，即在行驶过程中把车辆的加速度当作预测量，加速度的未来状态视为一种概率分布，而概率分布可以从过去的行车数据或标准工况中提取和归纳。计算当前时刻加速度概率向下一时刻转移的关键是计算出概率转移矩阵，其中，概率转移矩阵中的每一个元素分别代表了加速度从当前时刻向下一时刻转移的概率[11]，选取转移矩阵中概率最大值作为确定下一时刻的加速度值。

混合动力汽车行驶属于时间连续、状态离散的过程，令an为加速度的集合，可离散为有限的数值：

an∈{a1,a2,a3,…am}。

(18)

预测加速度的变化即是描述转移概率矩阵P(a,b)。

令向量

P(k+i)=(Pq1(k+i),Pq2(k+i),

Pq3(k+i),…Pqs(k+i))。

(19)

式中：Pqs(k+i)表示在t(k+i)时刻加速度大小在qs处的概率。因此可以得出以下关系式：

P(k+n-1)=P(k+n-2)PM=

P(k)(PM)n-1。

(20)

若在t(k)时刻，加速度大小τ(k)已知，所以P(k)已知，根据上式求出加速度在预测时域内各个预测点处的位置分布概率。

Pa,b的值能通过最大似然预测法确定：

(21)

(22)

a,b∈{1,2,…S}。

(23)

式中：M(a,b)为加速度从a转移到b的次数；Ma为加速度从a转移的次数之和。

将新欧洲行驶工况(NEDC)、城市道路循环工况(UDDS)、中国城市工况(CUDS)和全球统一轻型车测试规程(WLTP)4种工况作为样本工况来提取车速及加速度数据，得到了转移概率矩阵。图4示出由k时刻的加速度向(k+1)时刻转移的概率分布。

图4 马尔科夫链模型转移概率分布

根据建立的马尔科夫模型，可由当前k时刻的加速度预测出(k+1)时刻的加速度，并求出(k+1)时刻车速：

(24)

基于(k+1)时刻车速，在预测周期内不断更新预测区间，采用动态规划算法得到发动机和电机扭矩输出[12]，实现最优的扭矩分配，设第t0阶段预测时域th时刻优化目标函数为

ωv(v(t+1)-vtar(t+1)2)]dt。

(25)

式中：ωm，ωs，ωv为权重系数，SOCr为SOC参考值，vtar为预测车速。

同时对SOC进行约束，其表达式为

(26)

式中：α为常数，计算过程中取值105。

2.4 突变工况下的动态协调

经过上述分析，综合考虑研究对象的运动特性，马尔科夫模型预测方法在平缓工况下能有效预测未来车速，根据设定的目标函数进行扭矩最优分配，但在突变工况下此方法无效。因此，针对突变工况，本研究采用PID控制算法限制节气门开度变化率和电动机补偿差值扭矩的方法，有效地避免了燃油过度喷射和混合动力汽车模式切换过程中造成的冲击[13]。

通过PID控制算法限制节气门开度变化率，在突变工况下，整车控制器VCU对需求扭矩进行分配，当发动机控制器ECU接收到目标扭矩之后，对目标扭矩进行解析，将其解析成节气门开度β的指令。节气门开度变化率在单位时间内的增量是一个有限的数值，根据积分性质可知，若对未来一段预测区间内的节气门开度变化率Δβ进行积分，可得到具体的节气门开度数值。将节气门开度变化率Δβ作为PID控制器的输出，实现对发动机输出扭矩的控制，可表示为

|Δβ|=min{|Δα|,|kp·e+

(27)

燃油流量可以从具体的燃油效率Map图中通过下式计算：

(28)

式中：e=Te_tar-Te_act为发动机扭矩偏差控制量；Te_tar，Te_act分别为发动机的目标扭矩和实际扭矩；kp，ki，kd分别为比例、积分、微分增益系数；|Δβmax|为限制的最大节气门开度变化率。发动机的扭矩控制见图5。

图5 发动机的扭矩控制图

利用电机响应迅速的优点来补偿节气门动态协调控制中的差值，电机的目标扭矩为

Tm_tar=Treq-Te。

(29)

电机在输出扭矩时会受到自身的一些限制，因此对电机进行约束：

(30)

式中：Tm为电机输出扭矩；Treq为整车需求扭矩；Tm_max为电机的最大输出扭矩。

节气门开度调节过程中，发动机的输出扭矩为Te：

(31)

式中：Te_tar为发动机目标扭矩；Δβ为发动机节气门开度变化率；Δβlimit为发动机节气门开度变化率的限制值。

当发动机节气门的开度变化率大于Δβlimit时，对发动机进行动态协调控制，限制节气门的开度变化率在|Δβ|内，利用电机的快速响应特性来补偿减少的扭矩差值，同时保证两者的扭矩之和不会发生大的波动[14]，避免节气门突变时燃油经济性和排放的恶化。限制后的发动机和电动机动态扭矩控制结构见图6。

图6 限制后的发动机和电动机动态扭矩控制结构

3 仿真结果与分析

在Matlab/Simulink中搭建整车仿真模型，验证该策略的合理性。仿真过程中把能量管理控制策略的采样时间间隔设置为0.5 s[15]，同时设定预测时域P=6 s，电池SOC初始值为0.75，参考值为0.55。图7示出改进粒子群优化K均值聚类算法的工况分类动态协调控制策略示意。

图7 改进粒子群优化K均值聚类算法的工况分类动态协调控制策略示意

图8示出工况在线分类的仿真过程，在构建的循环工况中随机提取一段典型工况进行判别。由图8可知：车速加剧变化时，如在245—460 s,670—750 s和960—1 120 s，工况可判别为突变工况；而当车速在小范畴内波动或车速缓慢加减速时，如760—970 s，1 160—1 335 s和1 510—1 760 s，工况判别为平缓工况。由此可见，对工况进行分类的方法是有效的。

图8 在线工况判别结果

图9示出车速预测结果。由图9可知，通过对工况的在线分类和识别之后，能够较为准确地预测出该工况下的行驶车速。

图9 车速预测结果

为了更准确地评估预测值与真实值之间的误差，引入平均绝对误差MAE(Mean Absolute Error)作为评价指标。MAE表示预测值与真实值绝对误差的平均值，能更好地反映两者误差的实际情况，计算公式如下：

(32)

(33)

式中：MAE(k)为综合循环工况中第k个采样点在下一时域内的平均绝对误差；MAE为整个综合循环工况下的平均绝对误差；NC为综合循环工况下的采样点个数；va(k+i)为综合循环工况下第(k+i)个真实车速的采样点，误差范围0～0.5。图10示出预测车速和实际车速之间误差。

图10 预测车速与实际车速之间的误差

由图11仿真结果可知，针对综合循环工况，采用限制节气门开度变化率的动态协调控制策略后，车速和电机转速的波动仅为0.1 m/s和20 r/min。仿真结果表明，如110—190 s时间段加速度发生突变，经过动态协调控制策略控制之后，由油门突变引起的对传动系统的冲击明显减小，提高了模式切换时的行驶平顺性。

图11 动态协调仿真结果

建立动态协调控制策略的仿真模型，与传统的混合动力汽车进行对比分析，图12示出综合循环工况下发动机与电机的输出扭矩，图13和图14示出分类前后发动机的工作点分布。由图可以看出，采用该策略之后，车辆能够依据不同的工况合理地分配需求扭矩，在平缓工况下，发动机承担了几乎所有需求扭矩，并在高效率区运行；突变工况下，通过控制节气门的开度变化率，车辆更好地协调了BSG电机和发动机之间的扭矩分配，由于节气门开度变化更平缓，所以发动机也能够更好地维持在高效率区工作。

图12 发动机和电机的输出扭矩

图13 工况分类前发动机工作点

图14 工况分类后发动机工作点

从图15可以看出，经过工况划分后，车辆在保证了动力性的基础上，有效改善了燃油经济性。

图15 不同能量管理策略的燃油消耗曲线

本研究中，选取识别时间P=6 s，在WLTP工况下，与未采用工况分类的控制策略进行对比，对采用工况分类的控制模型编写m程序，并通过仿真模型调用程序。从图16至图18的仿真结果可以看出，驱动电机大多工作在25～55 N·m之间的高效区域，工作效率在89%以上，能有效提高系统的工作效率。

图16 综合测试工况电机工作点分布

图17 综合测试工况下电机扭矩

图18 综合测试工况下电机效率

图19示出电池SOC的仿真结果。工况的在线分类属于一种实时优化，能够合理地通过电池SOC的波动来调节发动机，保证发动机在高效区工作，并且电池SOC值变化平稳，保持在高效区0.5～0.7之间波动，既可以保证电池高效充放电，又可避免汽车在运行过程中由于动力电池SOC下降过快电机无法实现扭矩补偿的功能。本研究在保证了汽车的动力性与经济性的情形下，验证了动态协调控制策略的合理性。

图19 不同策略下电池SOC仿真结果

表2列出基于工况在线分类的能量管理控制策略。与未采取工况分类的能量管理控制策略的仿真对比，对节气门的开度变化率进行了限制，表中Q100表示综合测试工况下折合成的百公里油耗。与常规的混合动力汽车相比，采用本研究提出的基于工况分类的动态协调控制策略后，在整个综合测试工况下燃油消耗降低10.88%，表明该控制策略能够通过行驶工况的不同，合理地改善车辆在工作模式切换时带来的冲击，降低整车的综合燃油消耗。

表2 燃油经济性对比

4 结束语

混合动力汽车不同的行驶工况对能量管理策略控制效果的影响也不相同，因此，本研究提出了行驶工况在线分类判别的方法，将行驶工况分为平缓工况和突变工况，分类结果可为实现混合动力汽车动态扭矩协调控制提供理论基础。

平缓工况下利用马尔科夫模型进行车速预测，突变工况下对发动机节气门的开度变化率进行限制，大大减少了由于油门突变带来的动态油耗以及对传动系统造成的冲击，在改善了燃油经济性的同时，提高了行驶平顺性。

基于Matlab/Simulink仿真软件，建立整车控制策略仿真模型，验证了所提出的改进粒子群优化K均值算法进行工况分类的动态协调控制策略的合理性。结果表明，该策略可使汽车在行驶过程中，大大减小在突变工况下产生的动态油耗，同时电池的SOC下降速度明显降低，有效防止了汽车在运行过程中由于电池SOC下降过快，电机无法提供助力的问题。