住宅内部特征对房价指数影响研究与思考——以高层住宅楼层差异为例

□

在房地产价格统计调查中，新建住宅网签数据是以小区为单位进行分类汇总，通过加权平均计算每月房价指数。然而在实际操作中发现，此种方法忽略了同一小区内不同楼幢、不同住宅类型、不同装修标准甚至不同楼层间住宅的内部特征差异。本文以楼层差异对常州高层住宅的影响为例，尝试找出住宅内部特征对房价影响的一般规律，尝试找出研究类似问题的方法，为改进房价统计调查方法，进一步提高房价指数真实性提供参考。

|研究背景与意义

（一）新建商品住宅价格指数计算方法及问题

在现行房价调查方法制度中，房价指数计算方法是：先计算某一项目90 平方米及以下、90-144 平方米、144 平方米以上三个基本分类的环比指数，再将所有项目按照双加权汇总计算全市三个基本分类的环比指数，然后对这三个分类环比指数加权汇总，计算出新建商品住宅环比指数。

然而同一项目同一分类月度成交内部特征差异，导致均价环比存在非市场波动因素。一是销售房屋的位置、楼层、户型、朝向、装修程度等不同造成均价差异较大；二是部分特殊户型引起均价变动较大，如某幢住宅顶层户型价格普遍高于其他楼层，每平方价格高出上千元，这主要是由于顶层户型为复式且赠送面积较大，造成均价波动较大。还有一些是由于普通住宅和排屋、别墅价格的差异引起；三是尾盘销售，由于尾盘房源品质相对差些，加上回笼资金的需要，加大打折力度，造成同一楼盘环比价格差别。这些非市场因素一定程度上影响房价指数准确真实。

（二）楼层差异对价格影响研究现状

国外住宅别墅和低层洋房占比很高，对楼层的研究和关注度不高。在利用特征价格法计算房价指数时，中外官方机构及学者通常将总楼层这一特征简单归类为高层、中层、低层，或者直接忽略，对于所在层的关注就更少了，通常只考虑是否为底层或顶层。而当前我国高层住宅占比较高，对楼层差异的相关研究就具有较大意义，同时可填补这一空白。

（三）楼层差异对价格影响研究意义

房地产是国民经济的重要组成部分，对我国经济发展起着举足轻重的作用。在房住不炒的政策背景下，分析影响房价的因素，探究房价涨跌的原因对房地产市场的健康发展至关重要。真实可靠的房价指数是研究房价走势的重要指标。研究楼层差异等住宅的内部特征对房价指数的影响可有效解决前文所述相关问题，进一步提高房价指数真实性，可靠性。

因住宅的内部特征较多，本文主要以研究楼层差异对常州高层住宅房价的影响为主，其研究思路和结果可应用于住宅其他内部特征。

研究楼层差异对房价影响不仅对现行房价统计调查制度有参考意义，还能在一定程度上对开发商住宅定价、房屋价值评估等提供标准，也可对消费者购房时楼层选择提供参考。

（四）房价与楼层的一般关系

房地产价格是指建筑物连同其占用土地的价格，即房地产土地价格加建筑物价格，此价格是房地产市场运行和资源配置最重要的调节机制。影响房价的因素有经济因素、社会因素、政治因素、住宅内部特征和环境因素。楼层是内在特征中的一个方面。

从供应端看，总高不同的住宅建筑其平均建筑成本有明显差异，更高的楼层意味着更高的消防标准和安全标准，以及更多的水电等配套设施。客观上，房屋价格因不同楼层视野、日照、通风、噪音等方面的差异而有所不同。从需求端看，不同楼层便利程度、空气质量、堪舆（即风水）、电梯配比甚至楼层数字都会是购房者考虑的因素，从而对房价产生一定影响。横向比较，关于楼层的消费偏好各个国家甚至相同国家的不同地区和城市因文化和风俗习惯等的差异都有很大的差别。

|实证研究

（一）指标选择与数据来源

国家相关规定将10 层及10 层以上住宅定义为高层住宅。因10 层以下的住宅数据量小、且楼层差距对价格影响更为复杂，难以量化，故暂不做研究。

为了保证数据可靠性和可得性，尽可能保证数据完整，本文在2019年9 月到2020 年2 月常州市（不含溧阳）新建商品住宅（不含保障房）成交网签备案数据中随机抽取了5040 条成交记录。每条成交记录的均价记为p1，数据按照相同项目相同楼栋相同户型和面积进行汇总计算平均价格记为p2。因各个楼盘之间甚至不同楼栋之间价格差异较大，因此引入了两个均价的比值字段记为pr。pr 值的含义即为单套住宅均价占相同住宅不同楼层均价的比值，其值越大代表此套住宅价格相对其他楼层价格越高。需要说明的是，在数据汇总时，并不是所有项目楼栋的全部楼层都有成交，所以在选择数据时剔除了部分成交记录较少的楼栋。对于楼层，因为不同楼栋总层数不同，所以研究所在层数的绝对数对价格的影响在不同总层数的楼栋之间不具可比性。因此本文引入了相对位置的概念，相对位置包括在整栋楼中的楼层位置以及相对中间楼层的位置。楼栋的总层数记为zcs，所在层数记为szcs，所在层的相对位置即所在层数与总层数的比值记为cswz，距离中间楼层距离（计算方法为所在层数与二分之一总层数的差取绝对值然后除以二分之一总层数）记为zjwz。为研究特殊楼层，同时引入四个虚拟变量：1 楼、4 楼、18 楼、顶楼，分别记为F、F4、F18、FN，若符合楼层条件赋值为1，否则为0。表1 为数据导入STATA/SE 15.0后简单的数据描述。

（二）初步观察与分析

首先我们利用STATA 软件绘制各变量的矩阵散点图，观察各个变量两两之间的关系，如图1 所示。通过观察发现pr 和cswz 两个变量有正相关的线性关系，pr 和zjwz 两个变量可能存在负相关的线性关系。其余变量除有直接逻辑关系之外没有明显线性关系。这也和我们的常识基本吻合，即高层住宅越高层越贵，或者高层住宅越靠近中间层越贵。接下来用一元线性回归的方法具体研究。

表1 各变量的数据描述

（三）做一元线性回归

利用STATA 软件分别对pr 和cswz、pr 和zjwz 两组数据做一元线性回归，所得结果如表2 和表3 所示，cswz 系数符号为正代表相对价格高低与楼层高低呈正相关，P 值小于0.05 拒绝了原假设，代表整个方程是可信的。

再来看pr 和zjwz 变量回归分析的结果，zjwz 变量系数符号为负表示离中间楼层越远价格越低，P 值同样小于0.05。但R2值偏小且远远小于pr 和cswz 变量回归分析的R2值，拟合优度较低。

通过以上的简单分析，我们基本可以采信pr 与cswz 呈线性正相关的模型，即 pr=0.0725593cswz +0.9603831。其现实意义可简单解释为楼层越高相对价格越高。

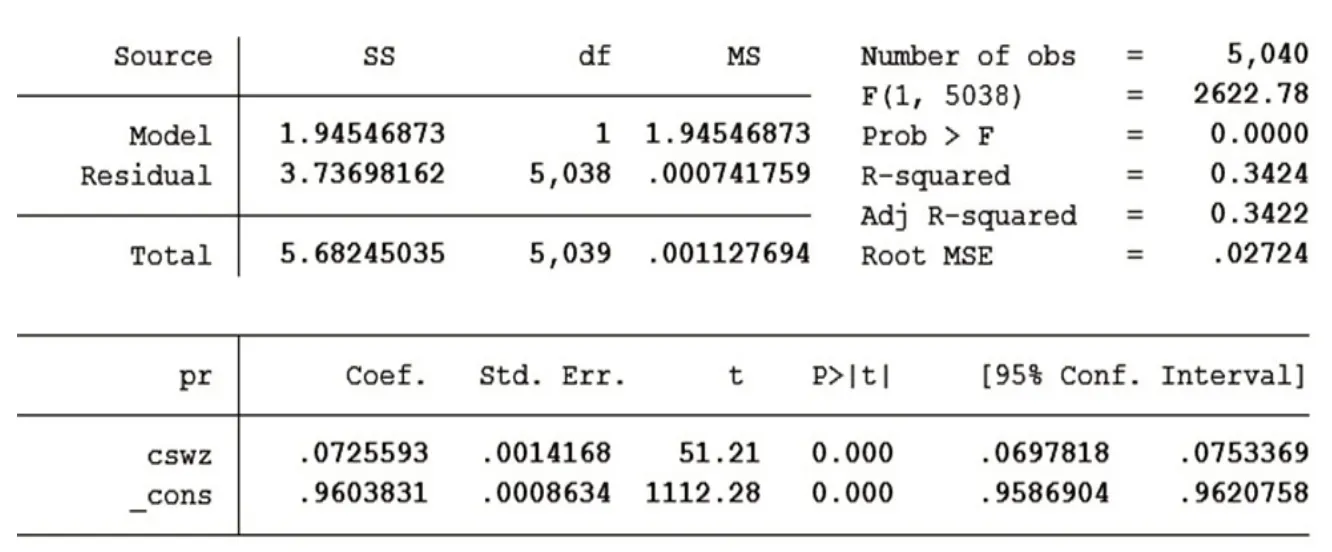
表2 变量pr和cswz一元线性回归分析结果

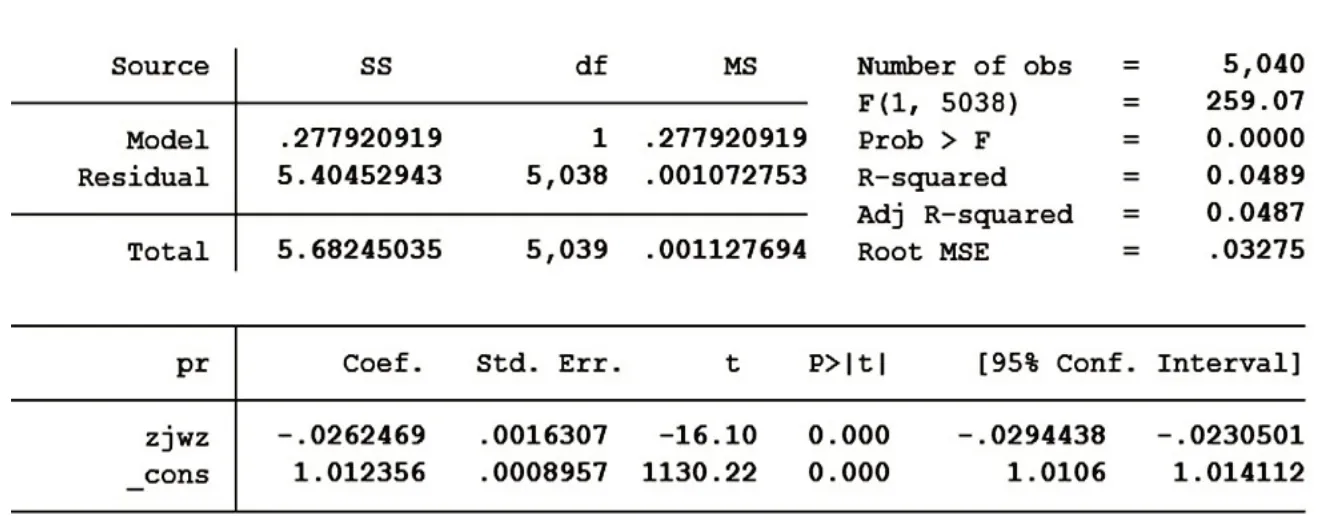
表3 变量pr和zjwz一元线性回归分析结果

（四）分析首层和顶层对价格的影响

图1 各变量的矩阵散点图

我们注意到图1 中首层和顶层有明显的偏低或偏高的数据，因此，我们借助前文的结果引入F 和FN 两个虚拟变量做多元线性回归分析。结果如表4：

结果显示，F 和FN 的系数符号均为负，代表首层和顶层均对房价有负面影响。同时我们注意到整个方程的调整的R2值为0.5130，相对0.3422 有了明显的提高，证明引入两个变量后方程的拟合优度更高。

（五）分析特殊楼层对房价的影响

为了研究特殊数字楼层对房价的影响，我们以4 楼和18 楼为例，进一步引入两个虚拟变量F4 和F18 进行研究。需要注意的是，18 楼有可能同时是顶楼。多元线性回归结果如表5：

与表4 的结果类似，F4、F18 变量系数的符号同样为负，证明4 楼和18楼对房价同样有负面影响。调整后的R2值进一步增大，拟合优度优于前式。

（六）实证分析结果

通过以上分析，结合实地走访调研的情况，我们可以得到以下结论：

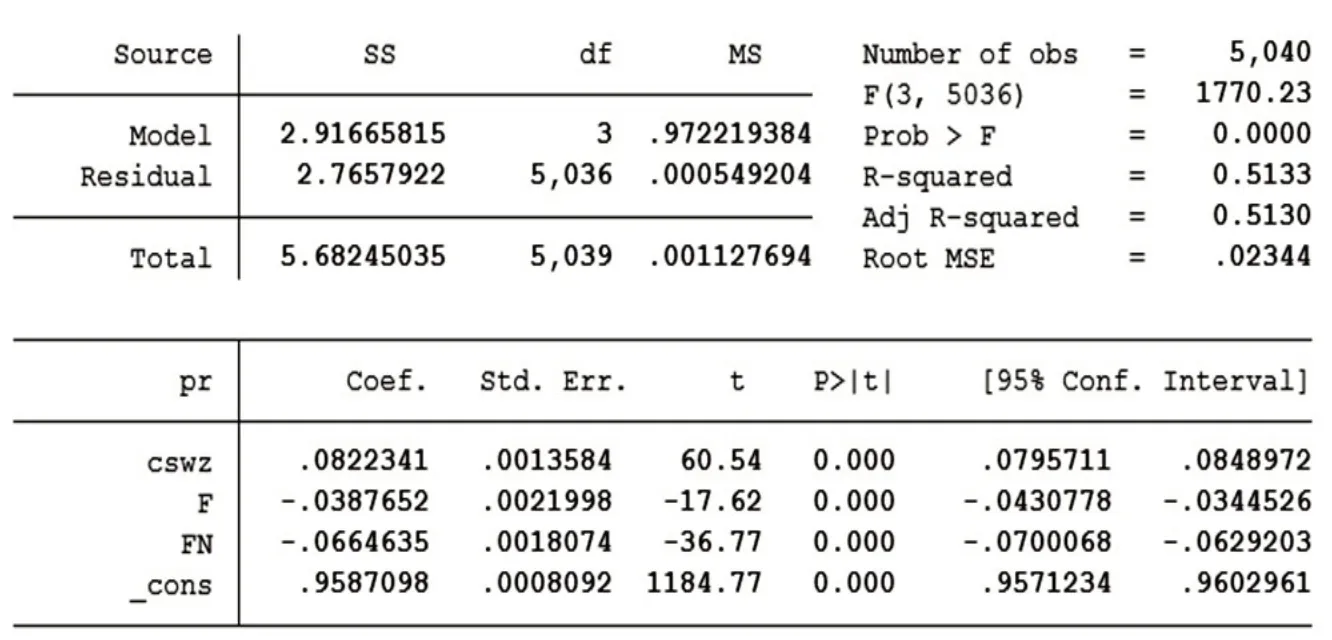
表4 变量pr、cswz、F、FN线性回归分析结果

表5 变量pr、cswz、F、F4、F18、FN线性回归分析结果

在其他条件相同时，房价与所在楼层数呈较强的正相关，与距离中间层的距离呈较弱的负相关。同时首层和顶层会显著拉低住宅价格，一些特殊楼层也会对价格产生一定负面影响。

在图1 中，一些首层和顶层呈现异常高价。结合之前的实地调研，分析可能的结果是部分首层会赠送庭院，顶层送阁楼或者楼顶使用权，导致价格较高。

在表1 的数据描述中，可以发现首层的频数占比明显低于本应该相等的4 楼成交数占比。原因一方面是一楼相对的销售周期会比较长，通常会比普通楼层长数周甚至数月，导致在数据提取和筛选时没有包含部分跨统计周期的备案数据，另一方面是部分开发商会将传统意义的一楼建为车库或其他设施导致一楼相对数量少。

根据表5 的结果我们可以得到楼层位置与相对价格的一般关系：pr=0.080286cswz -0.0403764F -0.0108292F4 -0.0065108F18 -0.0656799FN+0.9604305。取极值得到pr 最大最小值的比值为112.75%，也就是说因楼层差异相同住宅价格平均最大相差12.75%。此结果基本接近实地调研的真实情况。这说明，在样本较少的极端情况下，单个项目价格的环比指数可能会偏离正常值12.75%。

|相关思考和探索

（一）结合数据分析和实际工作经验，高层住宅首层和顶层等劣势楼层交易周期相对较长，通常会跨不同统计周期。而此类住宅的价格通常明显低于同幢住宅平均价格，在现行房价调查制度下，会在一定程度上拉低房价指数。建议可以采用加权或者剔除的方法消除特殊楼层对指数的影响。

（二）以项目为最小单位分类汇总新房网签数据直接忽略了项目内部特征的差异，而这些差异足以影响房价指数的准确性。可以此文的相关结论和模型为基础，采用对相应楼层的住宅赋予不同权数等方法优化房价指数计算方法。

（三）扩展到住宅其他内部特征，可以采用加权平均和特征价格法相结合的方式计算指数。即总的加权平均的计算方法不变，但在项目内部，采用特征价格法的思路，将项目内部的各个特征赋予不同的系数或权数。比如装修标准，将同项目内不同装修标准的住宅赋予不同的权数参与指数计算。以此类推，用特征价格法计算各项目的指数，再加权平均计算总指数。