可收卷复合材料层板大变形弯曲性能研究

周 震，程小全，张 涛，陈 磊，吴永康

(1. 北京航空航天大学航空科学与工程学院，北京 100083；2. 上海卫星工程研究所，上海 201109；3. 航天特种材料及工艺技术研究所，北京 100074)

近年来，先进复合材料在航空、航天飞行器结构中的应用比例不断增加，其中平面编织复合材料(又称编织布)越来越多地用于现代飞行器及结构中[1]。编织复合材料具有许多优点，如密度低、疲劳性能好、材料性能可设计性强以及柔韧性可控等[2]。与单向带复合材料相比，编织复合材料从结构形式到材料性能、损伤形式等均有很大差别[3]。编织复合材料会在一定的加载模式下表现出高度非线性行为，在大幅度弯曲时会更加明显[4]。

英国的RolaTube 公司于1998 年用编织复合材料开发出了一种可收卷智能结构，这种结构可以在可变换的两种稳定形态下交替使用：一种形态是可承力的舒展结构；另一种则是实现收藏功能的紧密卷筒结构。它们已广泛用于便携式支撑杆、机械臂和通信天线骨架等结构中[5]。

对于可收卷复合材料薄壁结构的研究一直是空间结构研究的重点之一，其原因是机械连接会破坏纤维的连续性[6]，而由复合材料薄壁结构制成的可收卷结构比强度、比刚度高，在没有展开机械机构辅助的条件下，就可以在到达轨道后实现展开，是执行空间任务的理想结构。可收卷复合材料结构在高功率太阳能电池阵列、相控阵天线、重力梯度杆、太阳帆等空间结构中已经或正在得到应用[7]。

可收卷复合材料结构在使用过程中会发生很大的弯曲变形，结构及材料都表现出高度的非线性，这与复合材料结构传统使用性能相距甚远[8]。研究表明，传统的复合材料结构失效分析方法不适用于薄壁层板大变形弯曲性能分析，因为纤维在大变形情况下呈现出高度的非线性的[9]。

目前对于复合材料在大变形条件下的研究，大部分侧重于理论研究，试验研究较少。Takano等[10]在分析复合材料在大变形下的力学行为时假设微观结构在局部区域变形均匀，建立了宏观和微观模型，并得到了试验验证。Xing 等[11]建立了大变形条件下不同变形速率的非线性本构模型，以表征聚合物基复合材料非线性大变形拉伸渐进损伤的相关行为。Aboudi 等[12]建立了一种宏观本构方程，用来预测复合材料在大变形超弹性阶段的静态稳定性失效问题。Xue 等[13]建立了一种基于复合材料的微观结构的细观和宏观本构模型，用来预测复合材料在大变形过程中力学性能。Upadhyay等[14]研究了在均匀横向压力作用下复合材料平行四边形板的大变形弯曲特性，结果表明平行四边形板处于大偏斜角(大于45°)时非线性效应占主导地位，处于小偏斜角(小于45°)时非线性效应则不明显。Peterson等[15]对可展开的碳纤维复合材料薄板的弯曲性能进行了试验研究，用解析法对其弯曲刚度进行了分析，并得到了试验的验证。Cui 等[16]研究了球拱型复合材料薄壳结构的在横向载荷下的大变形行为，试验发现变形形状一开始便已经产生，并逐渐扩展成最终的形状，且在屈曲变形之前发生了分层。截止目前，还鲜有看到有关复合材料薄壁层板大变形疲劳性能的研究报道。

本文将对玻璃纤维编织复合材料层板在大变形条件下的弯曲静力学性能和疲劳性能进行研究。因为现有的应变片量程一般只有15000 με，而复合材料层板大变形时的最大应变高达20000 με以上，市场上可以测量大应变的应变片价格偏高，所以为控制成本，在疲劳试验之前先进行静力试验，据此建立有限元模型来模拟薄板的静态弯曲行为，使模拟的应变结果在应变片量程范围之内与试验结果吻合，以保证模型的有效性。根据有限元模型计算的结果，选取合适的载荷进行疲劳试验，研究不同铺层薄板的疲劳性能和相同铺层层板的疲劳寿命曲线，旨在为复合材料可收卷层板的设计与寿命评定提供参考。

1 大变形弯曲静力试验

1.1 试件

本试验在参考ASTM D790[17]、ASTM D7264[18]和GB/T 3356[19]等复合材料层板弯曲试验标准后，根据可收卷复合材料层板实际使用中须承受剪切力的要求，确定使用三点弯曲加载方式。

考虑到夹具的尺寸和试验件在加载过程中产生的变形和滑移，将试验件的名义长度定为140 mm，名义宽度定为50 mm，如图1 所示。

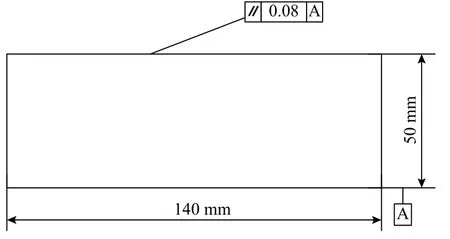
图1 试验件形状与尺寸Fig.1 Shape and size of test specimens

试验件材料有SW-100/9368 和SW-200/9368(玻璃布/环氧树脂)两种，仅单层厚度存在差别，分别为0.1 mm 和0.2 mm。试验件的铺层顺序及数量如表1 所示，试验件的铺层顺序为两种材料及(0°/90°)和(±45)两种方向的组合，此外还有一组表面加了一层0.7 mm 聚氨酯的试验件，用来研究表面保护能否增加试验件大变形弯曲下的疲劳寿命。

试验件中[(0°/90°)]8层板和[(±45°)]8层板各1 件用于静力试验，所有铺层层板各3 件用于测试相同载荷下的疲劳寿命及失效形式，余下的[(0°/90°)]8层板和[(±45°)]8层板各6 件用于测试它们在其他载荷下的疲劳寿命。

表1 试验件铺层顺序与数量Table1 Stacking sequences and number of test specimens

1.2 试验与测试方法

静力试验在Instron8801 液压伺服疲劳试验机上进行，利用应变片和试验机自带位移传感器分别测量试件在跨距60 mm 和80 mm 时的应变与挠度。应变测量点位置如图2 应变片位置所示，试验夹持及加载情况如图3 静力试验夹持与加载所示。

图2 应变片位置Fig.2 Positions of strain gauges

试验机的加载速度为4.0 mm/min，连续加载直到应变达到应变片量程值。卸载后观察应变数据能否归零，如不能归零，说明应变片已经出现损坏，需要重新贴应变片或更换试验件进行试验。

可收卷复合材料层板是以弯曲大变形来实现收卷与展开功能，实际使用中，一般是弯曲到某一固定形态而不是施加固定的载荷。为了模拟真实情况，试验时用位移(变形量)对其进行加载，并测量试验件应变与挠度的关系，而不控制或测量载荷。

图3 静力试验夹持与加载Fig.3 Clamping and loading in the static test

同样，在进行疲劳试验时采用位移加载方法。疲劳试验使用如图4 疲劳试验装置所示的自制的试验装置进行加载与测量。

图4 疲劳试验装置Fig.4 Setup of fatigue tests

三点弯夹具的下支座固定，上压头与曲柄滑块机构连接，并在中间安装载荷传感器，电机通过驱动曲柄滑块机构实现对试验件的循环加载。位移量通过曲柄滑块机构调整后固定，载荷则由载荷传感器测量。试验中电机的初始频率为10 r/min，若试验件没有产生错位移动等异常现象，则将电机频率增加到100 r/min。

此外，大变形弯曲会出现试验件与下支座产生横向(垂直试件长度方向)滑移，疲劳试验中长时间的滑动摩擦还会磨损试验件，并使试验件沿纵向逐渐偏离初始位置，所以需要在下支座上设计防滑移装置，并在试验件与下支座的接触部分涂抹润滑黄油，以减少滑动摩擦。

1.3 静力试验结果与分析

将3 个应变片测得的应变数据取平均值，[(0°/90°)]8层板在跨距60 mm 和80 mm 下及[(±45°)]8层板在跨距60 mm 下的应变平均值随位移的变化如图5 所示。

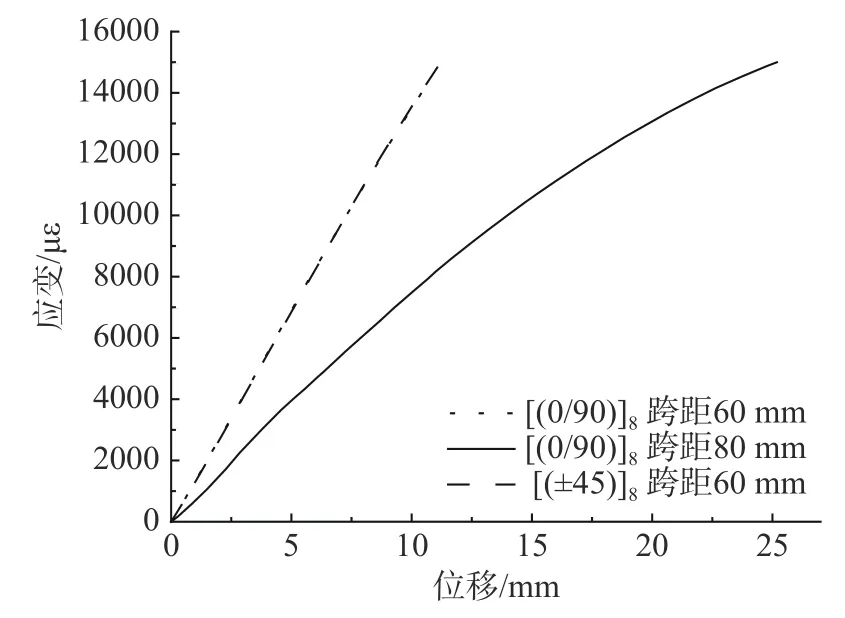
图5 应变-位移曲线Fig.5 Strain-displacement curves

从应力-位移曲线可以发现，大变形条件下，试验件中间段的应变与位移呈现非线性关系，且随着位移的增大，曲线的斜率越来越小。对比[(0°/90°)]8层板在跨距60 mm 和80 mm 的应变-位移曲线，可以看出跨距对试验件的应变-位移曲线影响很大，且跨距越小，应变随位移的增大变化的越快。

对比两种铺层层板在跨距同为60 mm 时的应变-位移曲线，两者的应变-位移曲线几乎重合，最大偏差仅为1.4%。可见，[(±45°)]8层板和[(0°/90°)]8层板试验件应变和位移的关系与铺层方向无关。

2 层板大变形弯曲性能有限元分析

2.1 有限元模型

静力试验中使用的SW-100/9368 材料性能参数数据见表2。SW-200/9368 的E1和E2为21.0 GPa，其余与SW-100/9368 相同。

表2 SW-100/9368 材料弹性常数Table2 Elastic constants of SW-100/9368 ply

在ABAQUS 中建立有限元模型，模型中用半径为5 mm 的空心圆柱刚体模拟三点弯夹具，如图6 有限元模型所示。有限元模型通过对下方两个圆柱刚体施加固支的边界条件，对上方的圆柱刚体施加一个向下的位移载荷来模拟大变形条件下的三点弯静力试验具体的加载情况。

在厚度方向层板共有8 层，每个铺层划分一层网格，另外两个方向单元间隔设置为1.6 mm，最终划分出23040 个单元，单元类型为C3D20R。因为大变形弯曲时层板与支座的接触部位一直在改变，变化的几何形状与边界条件引起了层板应变的非线性响应，而ABAQUS 中的Nlgeom 参数适用于几何非线性，所以在分析步中将Nlgeom打开。

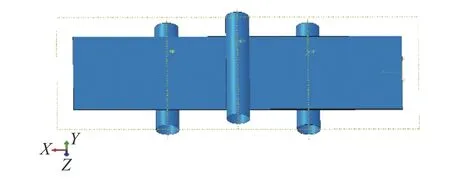
图6 有限元模型Fig.6 Finite element model

2.2 结果与分析

有限元模型计算得到[(0°/90°)]8层板沿长度方向的应变如图7 所示。中间段的应变最大，向两边逐渐减小，与实际情况吻合。

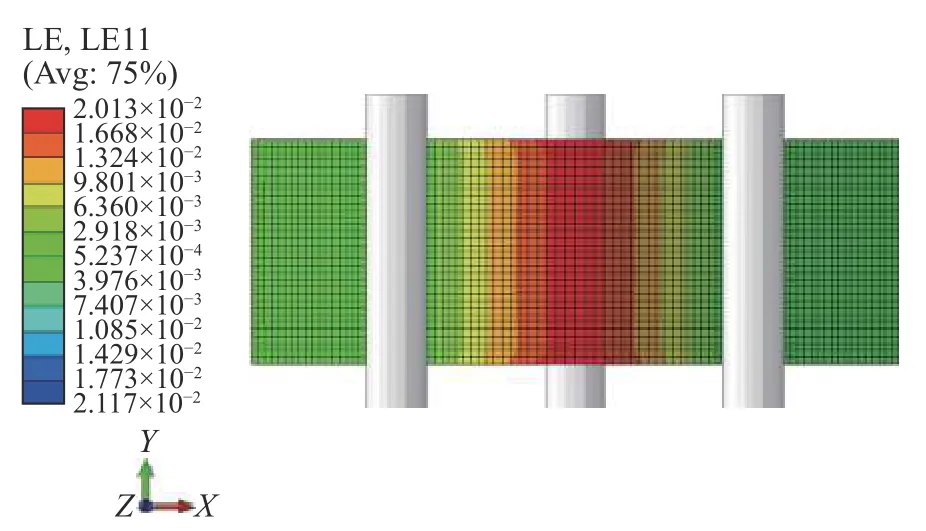
图7 [(0°/90°)]8 层板沿长度方向应变Fig.7 Strain diagram along the length direction of [(0°/90°)]8 plate

取加载过程中模型拉伸面长度方向应变的最大值，做出应变-位移曲线，并与试验得到的应变-位移数据作对比。[(0°/90°)]8层板试验与有限元模拟得到的在跨距60 mm 和跨距80 mm 情况下沿长度方向的应变-位移曲线如图8 所示。从图8 中也可以发现[(0°/90°)]8层板的非线性程度在跨距60 mm时大于80 mm。

改变模型中的铺层，得到[(±45°)]8层板沿长度方向的应变，如图9 所示。与[(0°/90°)]8层板类似，[(±45°)]8层板沿长度方向的应变也呈现出中间段的应变最大，向两边逐渐减小的趋势，但在中间段的上下边缘，出现了应力集中的现象。

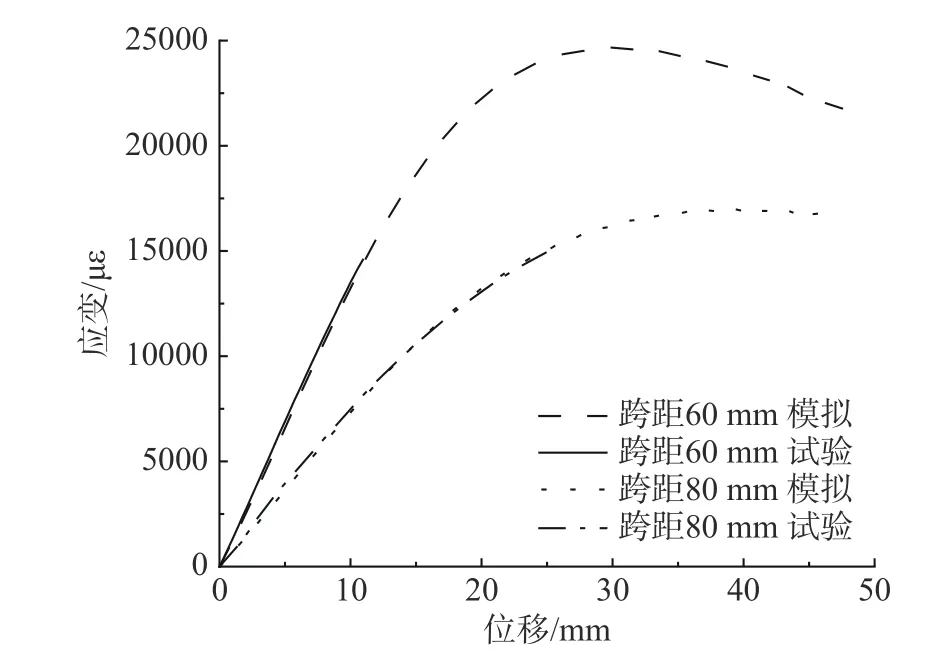
图8 [(0°/90°)]8 层板模拟与试验应变-位移曲线Fig.8 Simulated and tested strain-displacement curves of [(0°/90°)]8 plate

图9 [(±45°)]8 层板沿长度方向应变Fig.9 Strain diagram along length of [(±45°)]8 plate

取加载过程中模型拉伸面中心点沿长度方向的应变，作出应变-位移曲线，并与试验得到的应变-位移数据对比。[(±45°)]8层板试验与有限元模拟得到的在跨距60 mm 情况下沿长度方向的应变-位移曲线如图10 所示。

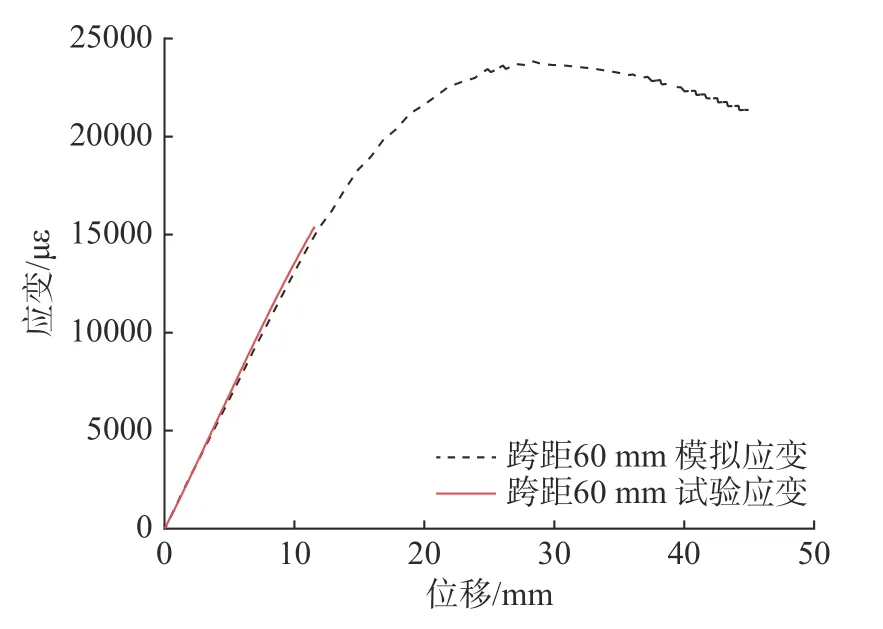
图10 [(±45°)]8 层板模拟与试验应变-位移曲线Fig.10 Simulated and tested strain-displacement curves of [(±45°)]8 plate

对比发现，有限元模拟得到的应变-位移数据与试验吻合得很好，[(0°/90°)]8层板跨距60 mm 时试验与有限元模拟之间的最大误差为4.2%，跨距80 mm 时的最大误差为10.6%，[(±45°)]8层板跨距60 mm 时试验与有限元模拟之间的最大误差为2.6%，均在可接受范围之内。基于上述分析，有限元模型计算得到的应变-位移数据与试验值趋势一致，误差较小，由此可以说明有限元模型的正确性。

有限元模拟中应变随着位移增加，呈现出先增大后减小的趋势，推测是由于开始时的位移量主要由层板的几何变形提供，所以应变迅速增加，而之后的位移量主要由层板的滑移提供，且两支座之间的层板长度增加，减缓了中间段的几何变形，所以产生了应变增加减缓直至不变甚至减小的现象。

跨距为80 mm 时，有限元模拟得到的最大应变仅为17000 με左右，跨距为60 mm 时最大应变则可以达到24000 με左右，而疲劳试验的应变需要达到20000 με，所以选择60 mm 作为疲劳试验的跨距。

3 层板大变形弯曲疲劳试验研究

3.1 不同铺层层板的疲劳寿命及失效模式

根据有限元模拟结果，选择跨距为60 mm，并选择最大应变20000 με，最小应变9000 με作为测试不同铺层弯曲疲劳性能的载荷，其对应的位移分别是16.76 mm 和6.76 mm。

在试验中，除试验件断裂破坏外，动刚度下降10%也是常用的疲劳失效判据之一。动刚度定义为一个加载循环内载荷差与位移差的比值：

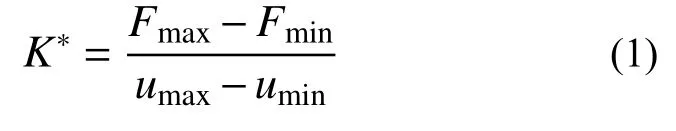
式中：Fmax和 Fmin分别为一个循环中的施加的最大载荷和最小载荷；umax和umin分别为一个循环中的夹头的最大位移和最小位移。

不同铺层层板在大变形条件下的疲劳寿命与失效模式如表3 所示。编号的前半部分表示表1中的铺层序号，后半部分代表该铺层的试验件序号。其中试验件7-1 的疲劳寿命与同组其他数据差别较大，予以舍去。

部分铺层同组之间的数据也存在着较大差距，说明该复合材料的弯曲疲劳寿命也存在着较大的分散性，这可能与复合材料层合板厚度的均匀性、内部初始缺陷和细观结构上的随机性有关。

为了显示更为直观，将各组的疲劳寿命平均后取对数，并整理为柱状图，如图11 所示，图中的横坐标为表1 中的铺层序号。

表3 不同铺层层板疲劳寿命与失效模式Table3 Bending fatigue life and failure mode of different laminates

从图11 中可以明显看出铺层3、6、9 和12的试验件疲劳寿命比较接近且大幅度超过其他铺层，其中又以铺层12 的试验件疲劳寿命最高。铺层3、6、9 和12 的纤维方向均为(±45°)，可见(±45°)铺层层板弯曲疲劳性能会显著大于(0°/90°)铺层层板。而铺层6 的单层厚度均为0.2 mm，疲劳寿命在4 种铺层中最低，破坏模式为纤维断裂和分层，可见完全使用厚度大的单层会使层板疲劳性能有所降低。

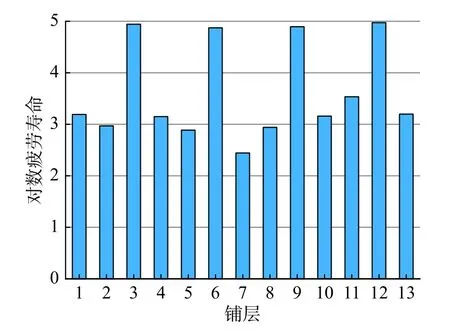
图11 不同铺层层板对数疲劳寿命Fig.11 Logarithmic bending fatigue life of different laminates

而对比铺层1 和13 的试验件可以发现，在试验件表面加入一层聚氨酯后，试验件的弯曲疲劳寿命基本没有变化，可见，聚氨酯对弯曲过程中的疲劳损伤没有明显的保护作用。

根据试验件的失效形式，可以发现最外层铺层为(0°/90°)的试验件均在疲劳试验过程中发生了纤维断裂。纤维断裂失效的如图12 所示，拉伸面的中间段出现了一条纤维断裂而形成的白色裂纹，压缩面中间段则出现了压缩破坏，且出现了较大面积的表面损伤。

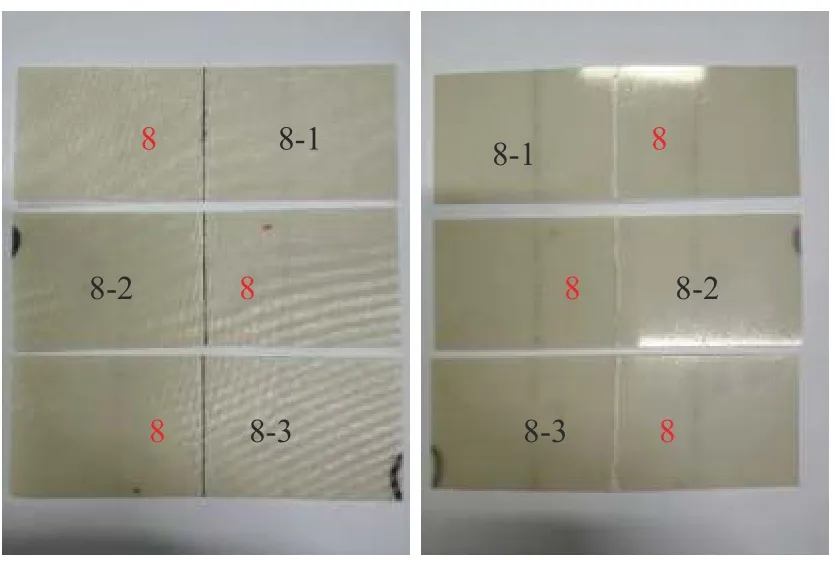
图12 纤维断裂失效模式Fig.12 Failure mode of fiber breakage

而除铺层6 外，最外层铺层为(±45°)的试验件在疲劳试验过程中均以动刚度下降10%而失效。[(±45°)]8层板试验件3-1、3-2 和3-3 在不同循环数下的动刚度如图13～图15 所示。将不同循环数下的动刚度测量点连接起来，可以在一定程度上反应试验件在试验过程中动刚度的变化趋势。三条曲线中动刚度均是在初期快速下降，然后下降的趋势变缓，最终变为初始动刚度的90%。

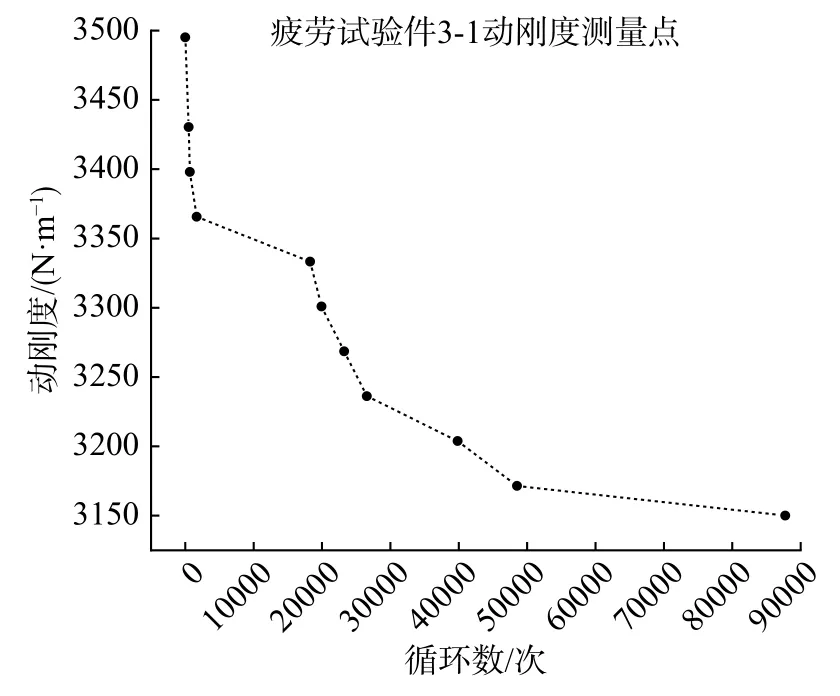
图13 [(±45°)]8 层板试验件3-1 动刚度-循环数曲线Fig.13 Dynamic stiffness-cycle number of [(±45°)]8 plate 3-1

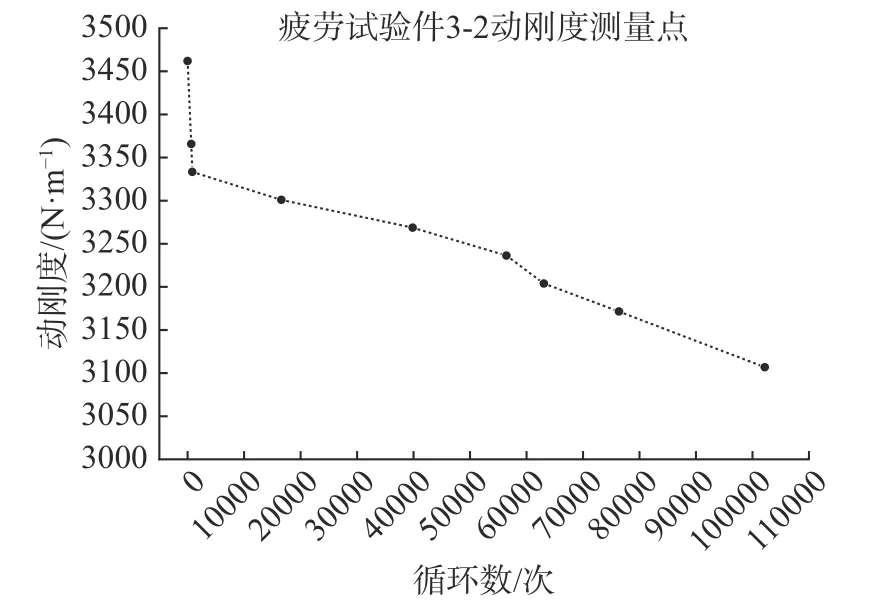
图14 [(±45°)]8 层板试验件3-2 动刚度-循环数曲线Fig.14 Dynamic stiffness-cycle number of [(±45°)]8 plate 3-2

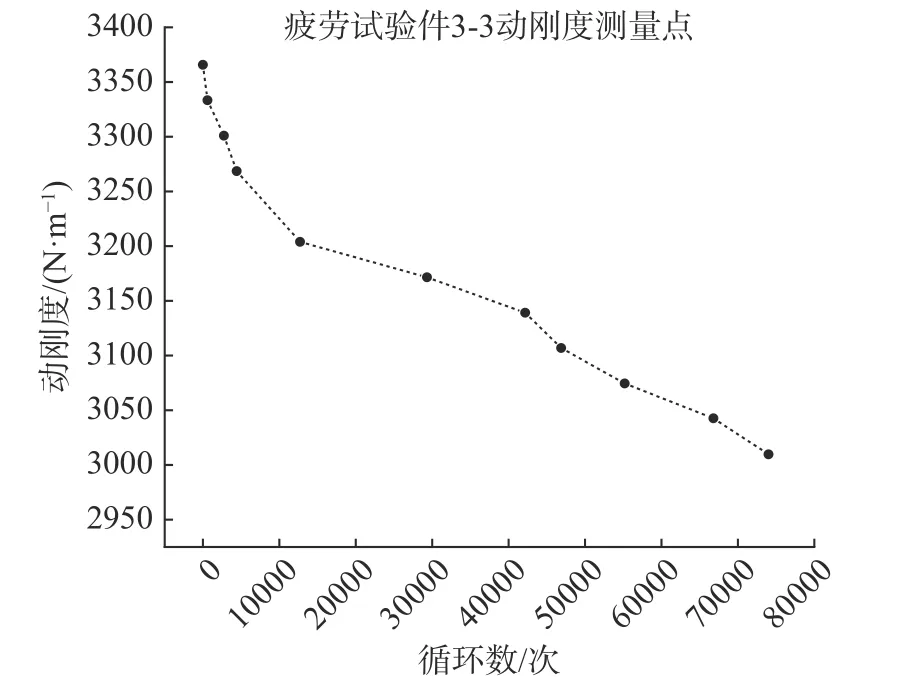
图15 [(±45°)]8 层板试验件3-3 动刚度-循环数曲线Fig.15 Dynamic stiffness-cycle number of [(±45°)]8 plate 3-3

3.2 相同铺层层板疲劳寿命曲线

保持最小应变和最大应变的比值不变，在其他载荷下对[(0°/90°)]8和[(±45°)]8层板试验件进行疲劳试验，并根据试验数据拟合出疲劳寿命曲线。试验加载中的最大和最小应变及对应的位移如表4 所示。

表4 应变及对应位移Table4 Strain and corresponding displacement

[(0°/90°)]8层板的疲劳数据如图16 所示， [(±45°)]8层板的疲劳数据如图17 所示，[(0°/90°)]8层板的失效形式均为纤维断裂，而[(±45°)]8层板的失效形式均为动刚度下降10%。

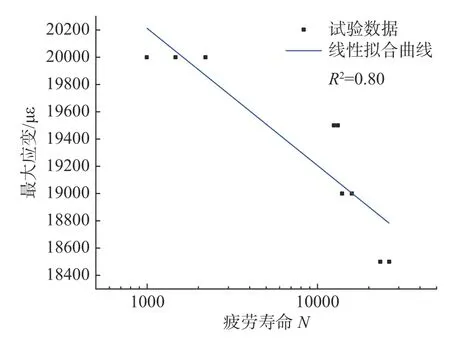
图16 [(0°/90°)]8 层板疲劳数据Fig.16 Fatigue life of [(0°/90°)]8 plate

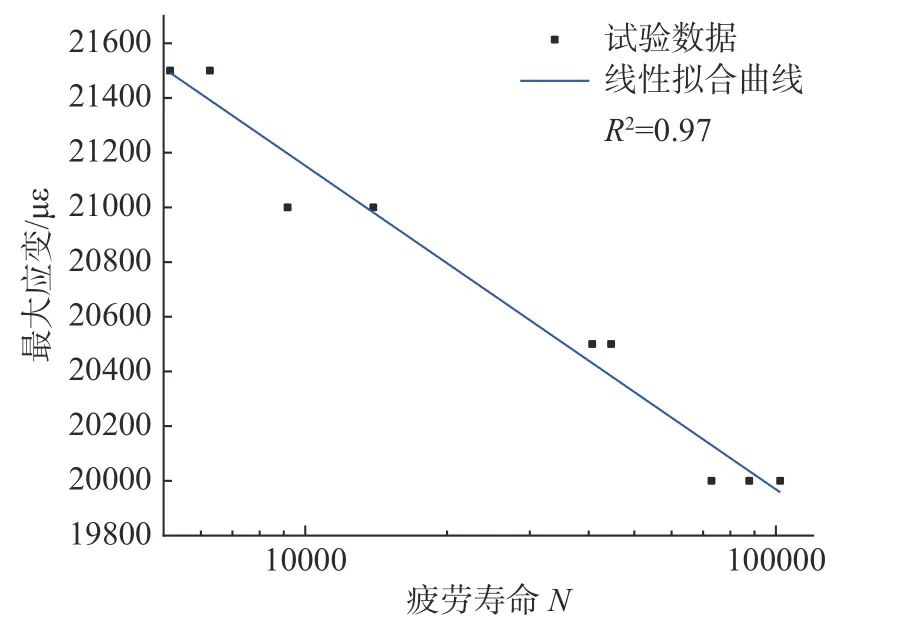
图17 [(±45°)]8 层板疲劳数据Fig.17 Fatigue life of [(±45°)]8 plate

两种复合材料相同铺层层板均有9 个有效数据，所有疲劳数据按照以对数寿命为横轴、最大应变为纵轴进行整理绘制。由于复合材料具有疲劳寿命分散性大的特点，为更加直观的阐明当前材料体系下疲劳试验数据的稳定性，在图中绘制出了基于一元线性回归方法的对数疲劳寿命-最大应变拟合曲线，并给出了其R2系数。[(0°/90°)]8层板疲劳数据拟合曲线的R2系数为0.80，而[(±45°)]8层板疲劳数据的R2系数为0.97，表明疲劳试验数据的线性拟合度较好，弯曲过程中的最大应变和对数疲劳寿命之间存在线性关系。

4 结论

可收卷复合材料结构能够在多种应用中代替机械机构，保持了纤维的连续性且增加了空间利用率，未来将在飞行器及空间结构中扮演越来越重要的角色。本文通过弯曲静力试验得到了层板在大变形条件下的应变和位移的关系，然后通过有限元模拟静力试验并与试验结果对照，确定了疲劳试验的载荷，最后研究了在大变形条件下不同铺层层板的弯曲疲劳寿命及失效形式和相同铺层层板的疲劳寿命曲线，得到以下结论：

(1) 在大变形弯曲下，复合材料层板的应变与位移呈现非线性关系，且跨距对试验件的应变-位移曲线影响很大，跨距越小，应变随位移的增大的越快。此外，通过对比[(0°/90°)]8层板和[(±45°)]8层板的应变-位移曲线可以发现，层板在应变片量程范围内的应变由几何关系决定，与铺层方向无关。

(2) 考虑到试验中层板变化的几何形状与边界条件引起了应变的非线性响应，有限元建模中将Nlgeom 打开并使用C3D20R 单元，由此建立的可收卷复合材料层板大变形弯曲性能有限元模型计算得到的应变-位移数据与试验值趋势一致，误差较小。

(3) 疲劳试验时，为了模拟可收卷复合材料层板在实际使用过程中只弯曲到某一固定形态，采用固定位移的加载方法，而非固定载荷。试验发现(±45°)铺层层板弯曲疲劳性能显著大于(0°/90°)铺层层板。最外层铺层为(0°/90°)的试验件的失效形式均为纤维断裂，而最外层铺层为(±45°)的试验件在疲劳试验过程中大部分以动刚度下降10%而失效。因此，在进行可收卷复合材料结构设计时，宜使用(±45°)的铺层，且应尽量避免全部使用厚度大的单层，以提高疲劳寿命。

(4) 在最小应变和最大应变比不变的情况下，[(0°/90°)]8层板和[(±45°)]8层板疲劳试验数据的线性拟合度较好，弯曲最大应变和对数疲劳寿命之间存在线性关系。