浮放花瓶动力反应机理与振动台试验研究

黄宝锋，华 夏，卢文胜

(1. 南京工业大学土木工程学院，江苏，南京 211800；2. 同济大学土木工程学院，上海 200092)

现行的抗震结构设计规范已经比较成熟，在建筑结构的地震破坏愈来愈得到控制的大趋势下，种类繁多的非结构构件尚缺乏系统的抗震研究工作，在地震中破坏现象极为常见[1 − 2]。据调查，酒店、办公楼和医院的非结构件成本通常占总成本的70%、62%和48%；Taghavi 等[3]调查发现：花瓶类陈设品、货架、橱柜等占建筑总成本的44%、20%和17%。这些物品(或设备)与地面或楼面之间通常没有机械锚固，容易受到来自楼面或地面动力作用的影响，因此在地震中往往损失严重。以汶川地震为例，据不完全统计，仅四川省就有216 家文物收藏单位的3169 件陈列文物(含一级文物16 件)受损。浮放类艺术品、馆藏文物等不仅具有经济价值，更具有艺术及文化价值[4]，因此对该类物品的抗震研究就显得极为必要。

浮放非结构构件在地震作用下的反应理论研究开展较早，Housner[5]以矩形刚体为分析模型，将其进一步简化为倒置的单摆，探讨其动力反应规律，得出了相对比较完备的解析解。Ishiyama[6]、Stonton 等[7 − 9]、赵桂峰等[10]和Gesualdo 等[11]对在地面运动下浮放物体的运动及其影响因素做了研究，其基本运动模式包括：滑移、摆动、跃起，以及多个运动的组合(如：滑移伴随摆动)。Wittich等[12 − 13]在研究偏心对浮放物体运动影响时发现，除了上述几种平面内的运动状况，还出现了平面外运动(平面外摆动、扭转)，这是由于偏心及接触面的缺陷造成的，在理想条件下不可能出现，故对该现象的讨论及研究较少。崔浩然等[14]对摇摆构件摇摆前的模型缺陷进行了分析。现阶段，对于浮放物品运动的研究大都聚焦于摆动反应，而对于相对滑移的研究则相对较少[15 − 20]。

振动台试验是验证分析结果，了解地震作用下真实地震反应规律的有效方法之一。Ishiyama[6,20]采用正弦波与地震波作为外部输入，研究摆动与倾倒的临界值问题。Winkler 等[21]采用有限元方法，研究了单个矩形木块和组合木块在简谐波和地震波作用下的地震反应，并进行了数值模拟。Konstantinidis 等[22]分析了6 层钢筋混凝土房屋的楼面地震反应，并将其作为输入波形，对3 种典型设备开展了振动台试验研究。Nagao 等[23]研究了高层建筑中非结构构件的抗震性能，对于打印机、储物柜、冰箱、书架等多种非结构构件开展了振动台试验，探讨其楼面滑移规律。周乾等[24 − 27]先后对馆藏文物的抗震性能开展了分析和振动台试验研究，并提出了各种有效的抗震措施。Fujita等[28]通过振动台试验和有限元的方法探讨导致刚块倾倒的理论解。Yeow 等[29]采用正弦波输入研究了办公桌在楼面运动下的滑移情况，结果表明，平均摩擦力-滑动位移关系呈现近似弹塑性规律。Isobe 等[30]针对5 种常用家具，开展了振动台试验，并用补偿法建立了数值模型。Sarhosis 等[31]研究了多层浮放圆柱地震作用下的表现，拓展了多层浮放非结构物的倒塌机理。

当前，非结构构件的抗震性能研究引起了科研人员的重视，然而对于浮放非结构构件的研究尚不够深入。主要存在以下几个问题：1)分析模型为已简化的平面矩形刚体，质量也均匀分布，与实际浮放非结构构件的形状和质量分布存在很大区别[32]；2)形状和质量分布不规则可能会导致既有的研究成果不再适用；3)既有的振动台试验研究并没有紧密结合理论分析成果，并对其进行验证或改进；4)浮放非结构构件的自由摆动规律与传统的建筑结构有很大区别，目前尚未对其开展针对性试验研究；5)当前的研究较少涉及馆藏文物类非结构构件，如各种珍贵瓷器、花瓶等；6)美国土木工程学会(FEMA E-74)[33]已经对抗震设计和分析方法做出了规定，而中国规范尚未对浮放非结构构件相应的设计和分析方法。因此，有必要在既有研究的基础上，解决这些科学和技术问题。对于浮放非结构物，浮放花瓶的动力反应机理和抗震性能具有普遍性和代表性，本文通过慢速推拉试验，获得花瓶的摩擦系数，通过振动台试验，探讨其地震反应特征，为制定浮放花瓶抗震措施提供试验基础和理论依据。

1 运动理论

1.1 运动模式

在地震激励作用下，浮放物体的运动模式主要包括：相对静止、相对滑移、摇摆、摇摆伴随滑移[9]。当无外部输入时，浮放物品(以立方体为例)受力平衡(图1)，当外部输入(ag)施加到一定程度，浮放立方体有顺时针摆动的趋势受力状况如图2。已知立方体高为h，底部宽度b，立方体重心处加速度为ab；假设浮放物体与接触面间动摩擦系数与最大静摩擦系数相等为µ。可通过对浮放物品受力情况的分析得到不同运动模式与相关因素的关系。

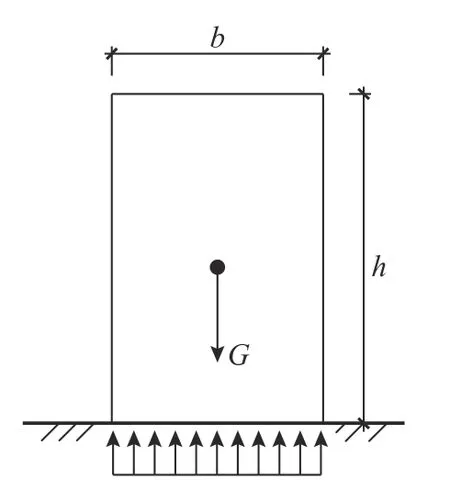
图1 静止状态Fig.1 Static condition

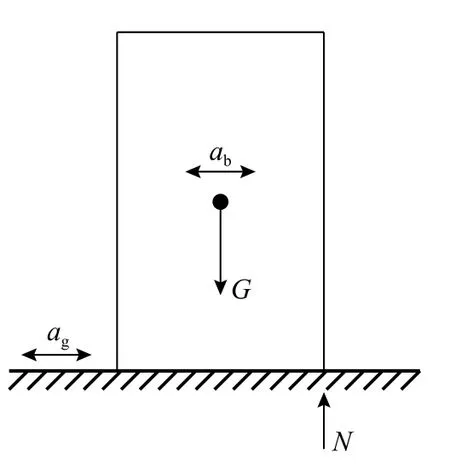
图2 摆动初期Fig.2 Rock starting

当接触面加速度较小，物体与接触面保持相对静止(ag=ab)，物体受力平衡，没有相对滑移：

此时浮放物体也不产生摆动，重力对转动点的力矩可以克服惯性力产生的矩：

化简得：

当接触面加速度增加，物体与接触面产生相对滑移(ag>ab)，但物体未摆动，根据受力条件可得：

化简得：

当物体与接触面不产生相对滑移(ag=ab)，但物体发生摆动，根据受力条件可得：

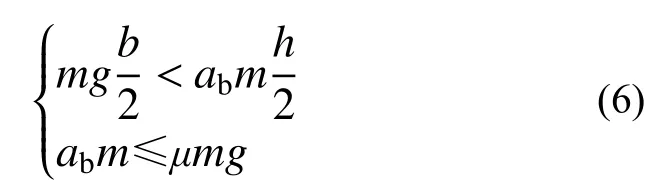
化简得：

当物体与接触面产生相对滑移(ag>ab)，且发生摆动，根据受力条件可得：

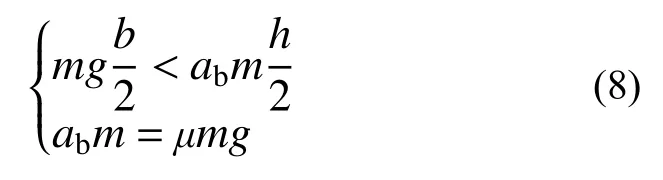
化简得：

运动模式的关系如图3 所示，显然，物体运动模式与物体自身的高宽比b/h、加速度峰值ag/g 和接触面与浮放物品间摩擦系数µ三个因素密切相关。浮放非结构物的几何形状(即高宽比)为物体的固有属性之一，不能改变。因而，可以通过调整另外两个参数，即摩擦系数和外部加速度输入的手段来改善或提高其抗倾覆性能(抗震性能)。需要指出的是：动摩擦系数和静摩擦系数在数值上差别很小，一般把动摩擦系数作为动力分析的主要参数。

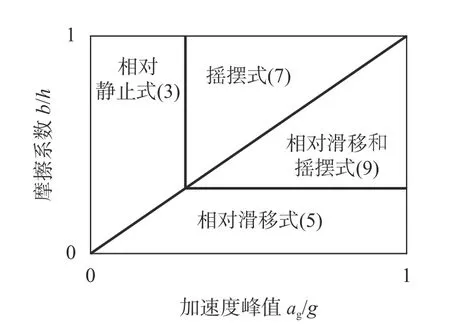
图3 运动模式Fig.3 Response mode

1.2 摆动方程

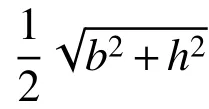
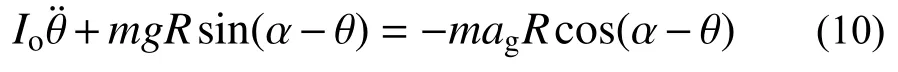
式(10)为二阶非线性方程，可将其线性简化或通过数值方式求得结果。当ag为0，初始释放角度θ0不为0 时，即为浮放物品自由摆动运动方程：

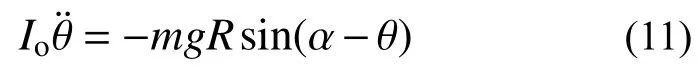
Housner[5]认为式中所涉及的角度较小，符合小角度假设，可对其进行线性化，则由式(11)可得：

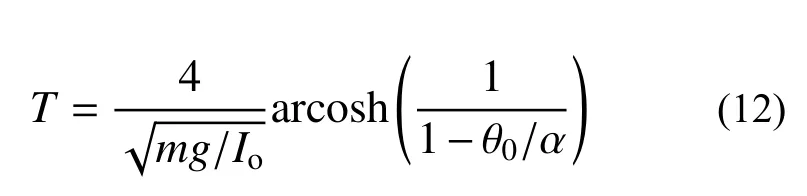
由式(12)可知，自由摆动周期与花瓶自身几何形状和初始释放角度θ0相关，因此，通过改变这两个参数可调整其振动特性。

式(1)～式(12)的基本假定为均匀平面矩形刚体，其重心与形心重合，适用于理想的平面刚体模型，对于浮放花瓶类体型和材质复杂的非结构构件，其适用性需通过振动台试验研究来校核。

2 几何形状和摩擦系数测试

2.1 三维扫描

本文研究对象为高1.25 m 的陶瓷花瓶(图4)，该类花瓶在住宅、办公室、酒店等建筑中常作为装饰品，是常见的非结构构件之一。相对于传统的建筑结构，花瓶表面具有弧度，几何形状复杂，难以运用传统的测量方法获得其几何参数。因此，采用了三维激光扫描仪(COMETL3D)对其空间尺寸进行观测(图5)，具体参数列于表1。其中，对应重心位置的确定(h0)，是将花瓶分成图5(b)所示的网格，采用离散积分的方法来确定，具体见式(13)，其中，mi为每个网格的质量，hi为每个网格到花瓶底部的距离，ci为每个网格的高度，Vi为网格的体积。

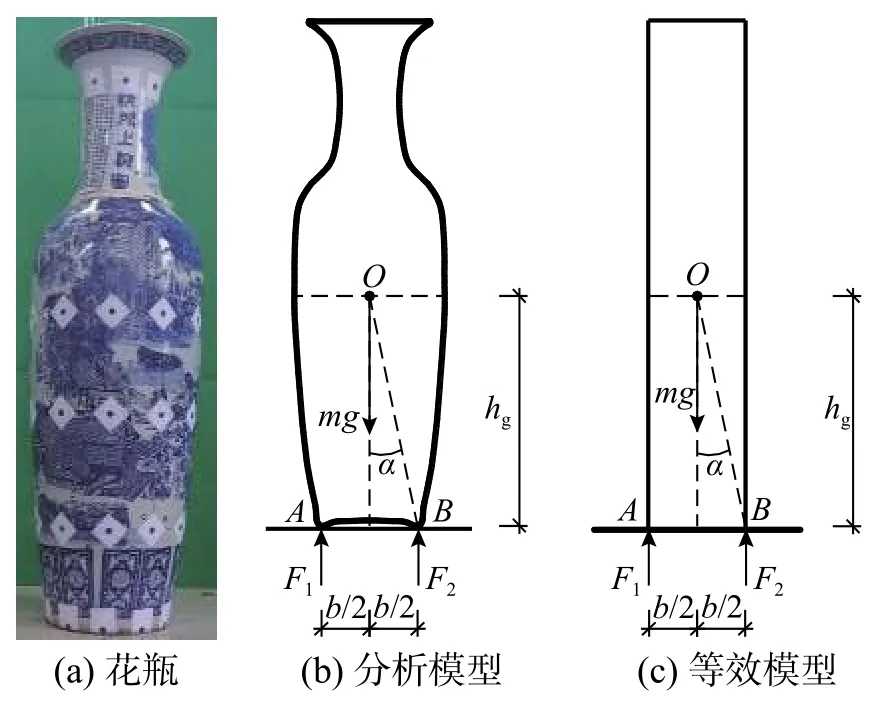
图4 花瓶模型Fig.4 Real and analytical model of the vase

图5 花瓶3D 扫描Fig.5 3D scanning of the vase

表1 花瓶几何参数/mmTable1 Geometric parameters of the vase

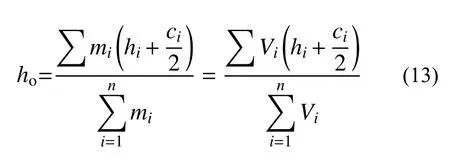
根据这些参数，可以对其动力反应特征开展计算和评估。

2.2 理论周期

将2.1 节中获得的浮放花瓶相关参数，代入式(12)，可得花瓶摆动周期与释放初角θ0的关系为：

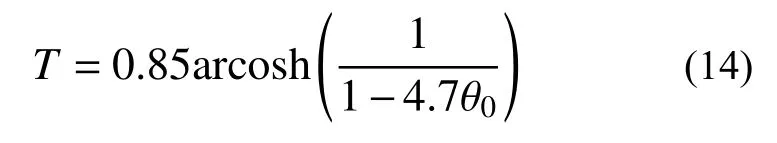
其关系如图6 所示，从此图可以看出，周期随释放角度的增加呈非线性增加，这一点与传统的建筑结构的周期特点不同。

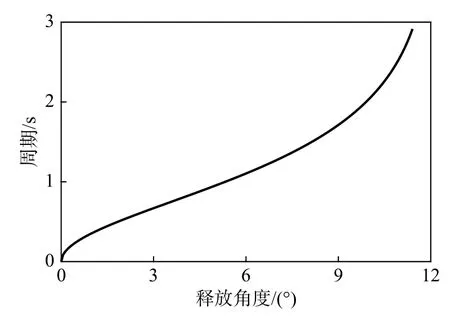
图6 周期与释放角度之间关系Fig.6 Rocking period and releasing angle

2.3 摩擦系数

从2.2 节可以得知，花瓶与接触面间的摩擦系数也是一个重要试验参数，花瓶运动的动力就来自于接触面的摩擦力[34]。测量摩擦系数的方式较多，慢拉试验是较为简洁且有效的方法。即用外力慢速推拉花瓶或其支撑面，使得两者之间产生相对运动，推拉力就是两者之间的摩擦力，再根据重力与摩擦力之间的关系，很容易求得摩擦系数的数值。将花瓶底部用套箍与拉力传感器连接，并固定在反力架上，花瓶下面则是安装在小车上的大理石板，通过缓慢推拉动小车使大理石板运动，保持拉力方向与钢拉杆方向在同一直线上，而花瓶相对地面静止，以此来测得两者间的动静摩擦系数(图7)。

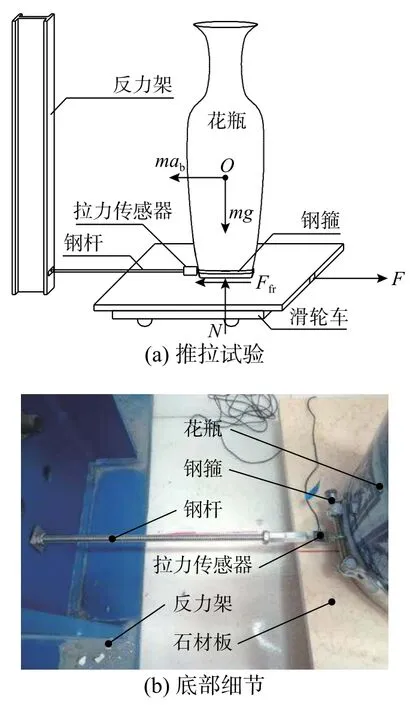
图7 摩擦系数测试Fig.7 Friction coefficient test

摩擦力测试结果如图5 所示，在开始阶段，随着拉力的逐渐增加，花瓶与大理石板间无相对位移，因此传感器读数也随之增大。在力加到一个最大值后两者发生相对运动，此时传感器显示力会有所下降。随后，花瓶在拉杆的拉力作用下与摩擦力平衡，相对反力架保持静止，传感器读数稳定在一个范围内。已知花瓶的质量为32.5 kg，可求出动摩擦系数为0.23，静摩擦系数为0.31(图8)。

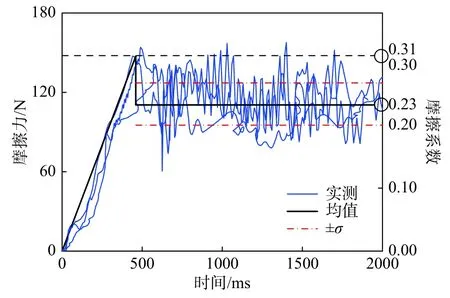
图8 摩擦系数Fig.8 The coefficient of friction

3 输入波形和试验工况

选择输入波形是振动台试验的重点和难点，浮放花瓶在建筑中可能的摆放位置有2 种，即地面和楼面，因此，输入波形也应该与这两种情况对应。振动台试验中选取了4 条波形：2 条历史地震波和2 条人工地震波。为了考核放置于地面的花瓶的地震反应，在NGA-West3 数据库中选取了El Centro(南北向)波[35]，其对应的地面加速度峰值为0.35 g(图9(a))，持续时间长且频谱丰富，在世界范围内广泛运用，具有一定的代表性。为了考核放置在楼面上的花瓶的动力反应状况，从美国强震数据库(CESMD)中选择了一栋7 层钢筋混凝土酒店(Van Nuys)的屋面加速度时程，该记录发生于1994 年1 月17 日Northridge 地震，加速度峰值为0.58 g，持续时间为59.98 s(图9(b))，该波形周期在0.35 s～2.2 s 时，反应谱加速度比较大，可见其长周期分量较为丰富(图10)。该波为实际楼面地震记录，其持续时间和频谱也比较丰富，具备一定的代表性，有利于考核花瓶在实际楼面地震作用下的动力反应特征[36]。另外2 条是根据AC156 人工拟合的波形[37]。由于建筑结构类型、高度、场地条件等因素均会对楼面地震动造成影响[38]，因此很难找到一个具有代表性的楼面波形用于振动台试验。AC156 是目前非结构构件或系统抗震鉴定的基本依据之一，适用于非结构体系的振动台试验[37]。因此，根据AC156 中推荐的目标反应谱合成2 条波形，1 条持续时间为60 s(图9(c))，用于研究放置在高层建筑上的花瓶的抗震性能[39]。另一条持续时间为30 s(图9(d))，可用于研究在多层建筑中浮放花瓶的抗震性能[40]。4 种运动对应的反应谱如所示。从图中可以看出El Centro 波的反应谱加速度峰值最小，当周期超过1.3 s 时，其加速度峰值迅速减小，因而并不具备长周期作用(Van Nuys)的效果。因此，所选4 条波形可以基本涵盖浮放花瓶所可能承受的楼面地震作用。

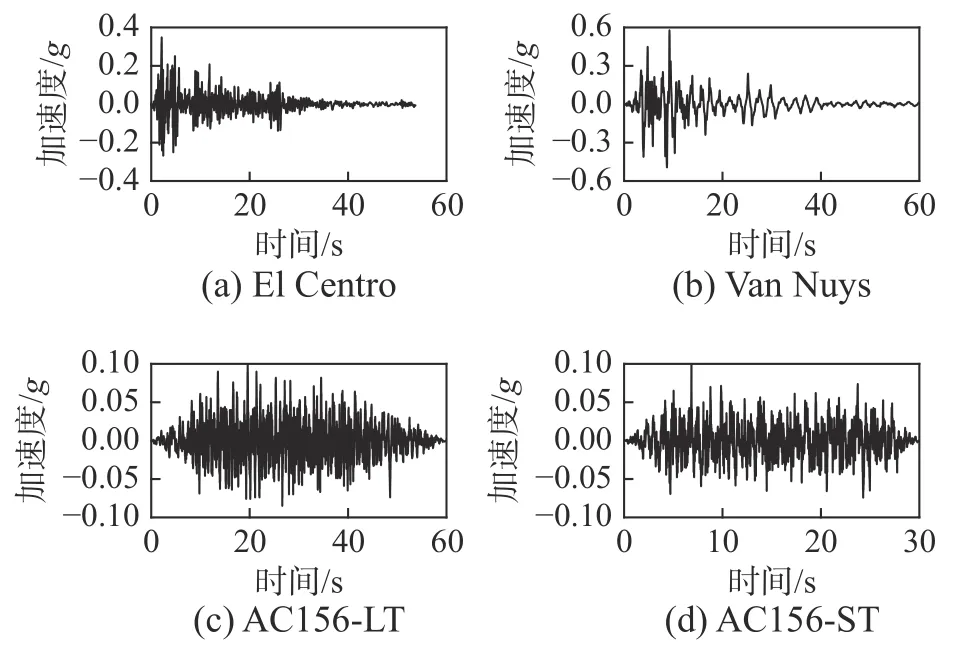
图9 加速度时程Fig.9 Input motions

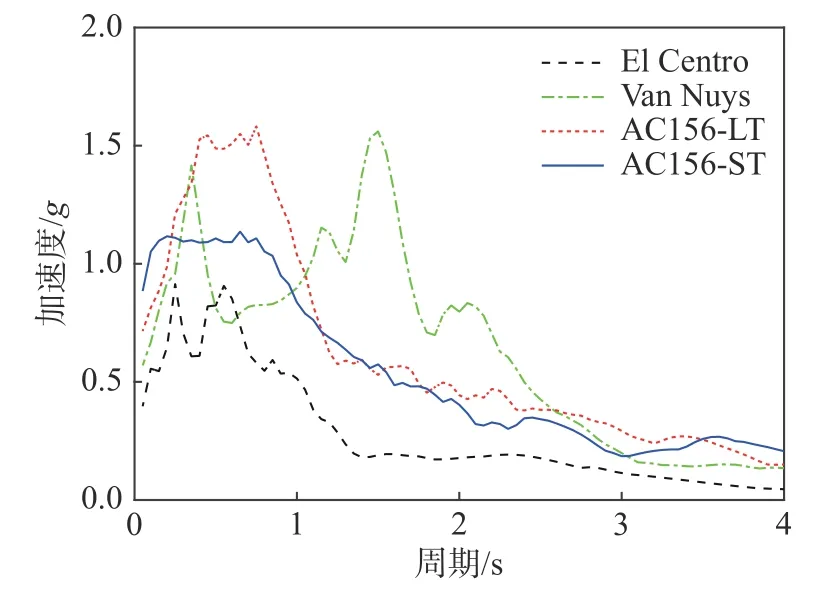
图10 加速度反应谱(ζ=0.05)Fig.10 Response spectra (ζ=0.05)

根据现行抗震规范[38]，三水准(多遇、基本和罕遇地震)的加速度峰值分别为0.035 g、0.1 g 和0.2 g。根据1.1 节所得结论，只有当输入加速度峰值大于动摩擦系数(0.23)与重力加速度的乘积时，才会发生相对运动[9]，峰值小于0.23 g 时，花瓶与地面将保持相对静止，因此，输入峰值从0.20 g 开始，略小于动摩擦系数与g 的乘积。人工波的输入峰值为0.2 g～0.6 g，天然波形的峰值均增大到实际加速度幅值，即El Centro 波和Van Nuys波分别增加到0.35 g 和0.58 g。试验工况见表2，其中，根据上文中提到的运动模式，在工况1～工况4中预期花瓶将保持相对静止，工况5～工况11 中预计花瓶将滑移且摇摆。本次试验中波形输入均为单向，试验过程中，采用加速度控制。

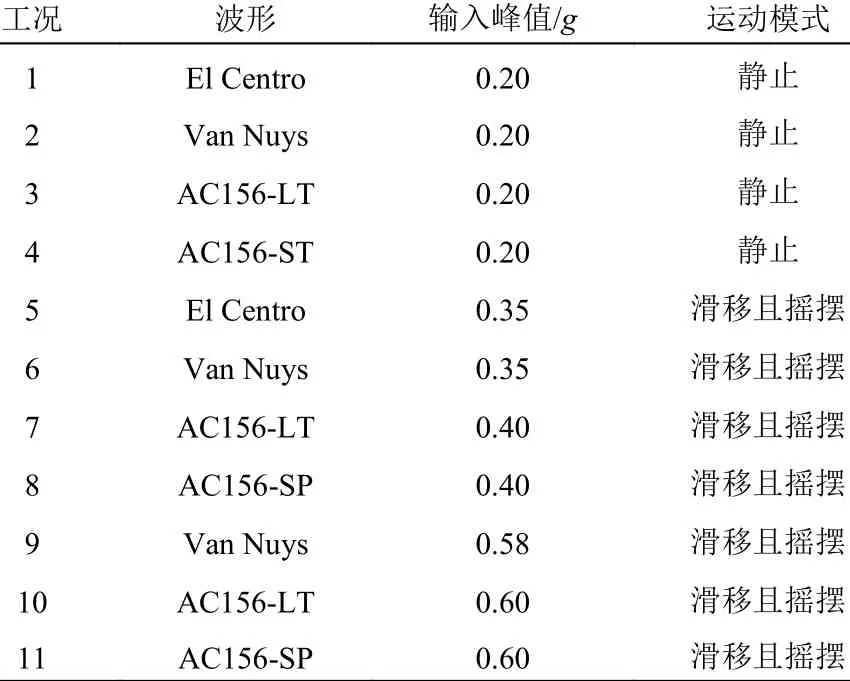
表2 试验工况Table2 Test Procedure

4 试验设备与观测

本试验采用单向、电液伺服振动台试验系统。振动台台面尺寸为80 cm × 80 cm，台面最大加速度1.0 g，最大载荷500 kg，最大水平位移为±20 mm，台面频率范围为0.5 Hz～100 Hz。

在大理石面板(1.0 m×1.0 m×0.02 m)四角用螺栓锚固在振动台上(图11(a))，模拟与花瓶的接触面。因考虑传统传感器的设置会对花瓶在振动台上运动造成较大的影响，故采用非接触观测手段，利用高速摄像机系统(ISM-CONTER-VG5-3D)来观测花瓶的三维运动(图11(b))。为了方便追踪，在花瓶底部、重心、颈部等代表性位置布置了24 个观测点(图11(c))。

5 试验结果

5.1 试验现象

在振动台试验前，通过对花瓶进行自用摆动试验，摆动时程曲线见图12。摆动角度通过花瓶上同一高度3 个点形成平面的法向量与YOZ 平面的夹角计算得到。从此图可以看出，花瓶的摆动周期为1.3 s 左右，与采用式(14)的计算值非常接近。

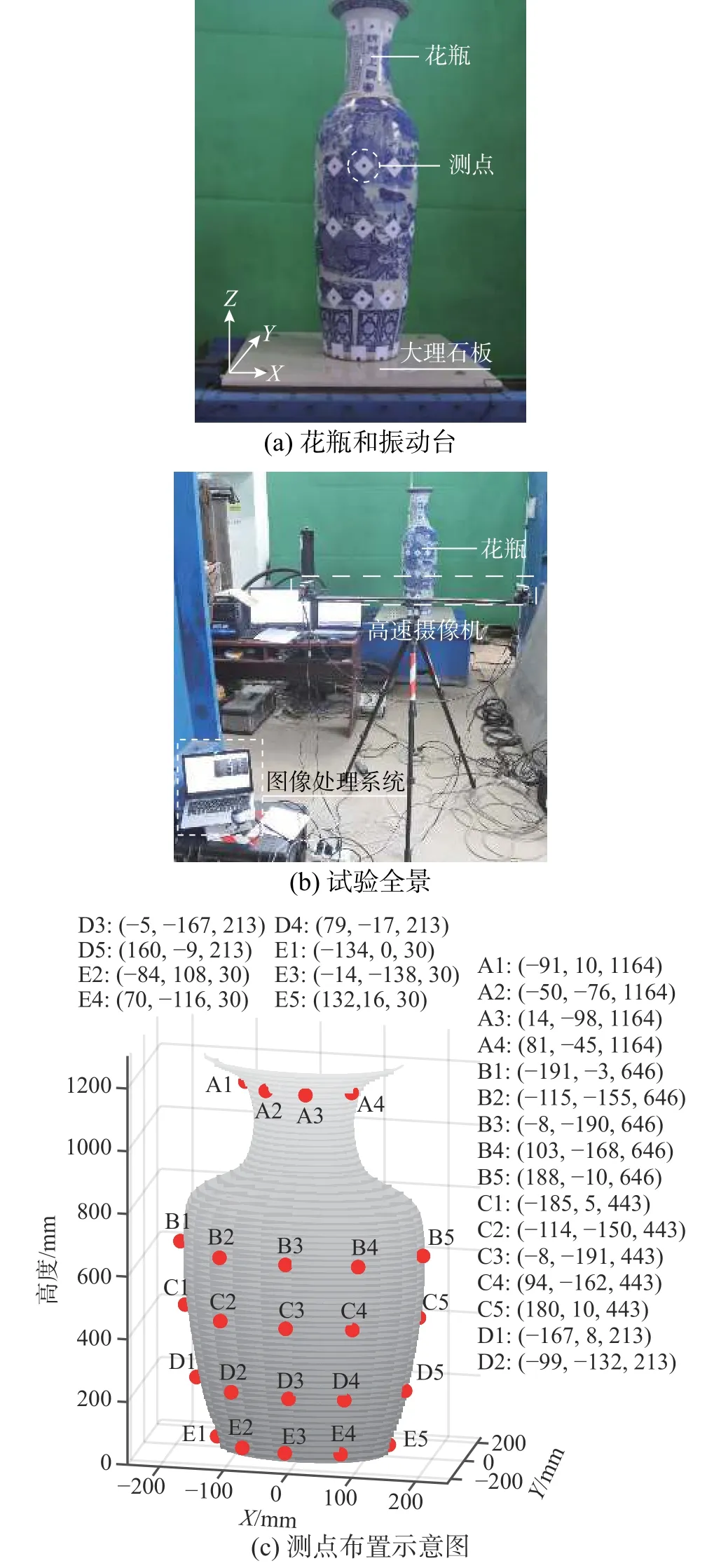
图11 振动台试验概况Fig.11 Test setup

振动台试验过程中，输入加速度峰值与摩擦系数的关系决定了花瓶的运动状态，与图3 中的理论运动模式基本吻合。当输入加速度峰值为0.2 g时(工况1～工况4)，输入加速度峰值小于动摩擦系数与重力加速度乘积时(0.23 g)，对应的位移反应较小，花瓶与地面之间几乎没有相对位移，但仍发生轻微振动，但花瓶与振动台台面相对静止，并未发生明显的相对运动该现象，虽然与1.1 节的分析结果有所出入，可能由振动台台面噪声所致。当输入加速度峰值超过动摩擦系数与重力加速度乘积时(大于0.23 g，工况5～工况11)，位移反应增加了很多，这一观察结果与1.1 节的分析结果较为吻合。花瓶与台面之间发生相对滑动并且开始摇摆。此外，与期望反应特征不同的是，花瓶在摇摆的同时发生了平面转动，说明其质心并不在其形心轴上，从而验证了其厚度并不是完全均匀。

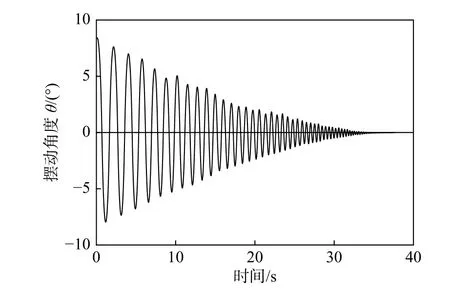
图12 自由摆动时程曲线Fig.12 Time history of free rocking

5.2 位移反应

位移反应为通过B 排测点与D 排测点计算所得的重心处的位移反应数据，通过该点能够反映出花瓶整体的运动状态。在4 种地震波作用下，观测了花瓶的位移反应。当输入波形加速度峰值小于动摩擦系数时，花瓶与台面几乎没有相对位移，超过动摩擦系数时，两者之间开始发生相对位移。两条天然波形作用下的位移反应如图13 和图14 所示。在El Centro 波作用下，花瓶表面测点竖向位移峰值为14 mm(图13)，表明花瓶已经发生了摆动。在三个方向的位移峰值分别为110 mm、38 mm、16 mm，且几乎在同一时间发生(第14 s)(图13(a))。花瓶的平面位移轨迹(图13(b))表明即使在单向地震作用下，花瓶除了滑移与摇摆运动，也发生扭转反应。引起扭转的原因可能在于：1)形心和质心不在同一点；2)接触面粗糙度不均匀。从而导致摩擦力合力作用方向与重心线不在同一竖直面内。在Van Nuys 波作用下也有类似的现象，但在数值上小于El Centro 波作用下的位移峰值 (图14)，当Van Nuys 波加速度峰值达到0.58 g 时，其三个方向位移峰值分别为83 mm、38 mm、9 mm。El Centro 与Van Nuys 作用下最终的位移值均为65 mm(图13(a)、图14(a))。此外，Van Nuys 波作用下的平面运用轨迹比El Centro 波稍微扁平些(图13(b)，图14(b))。

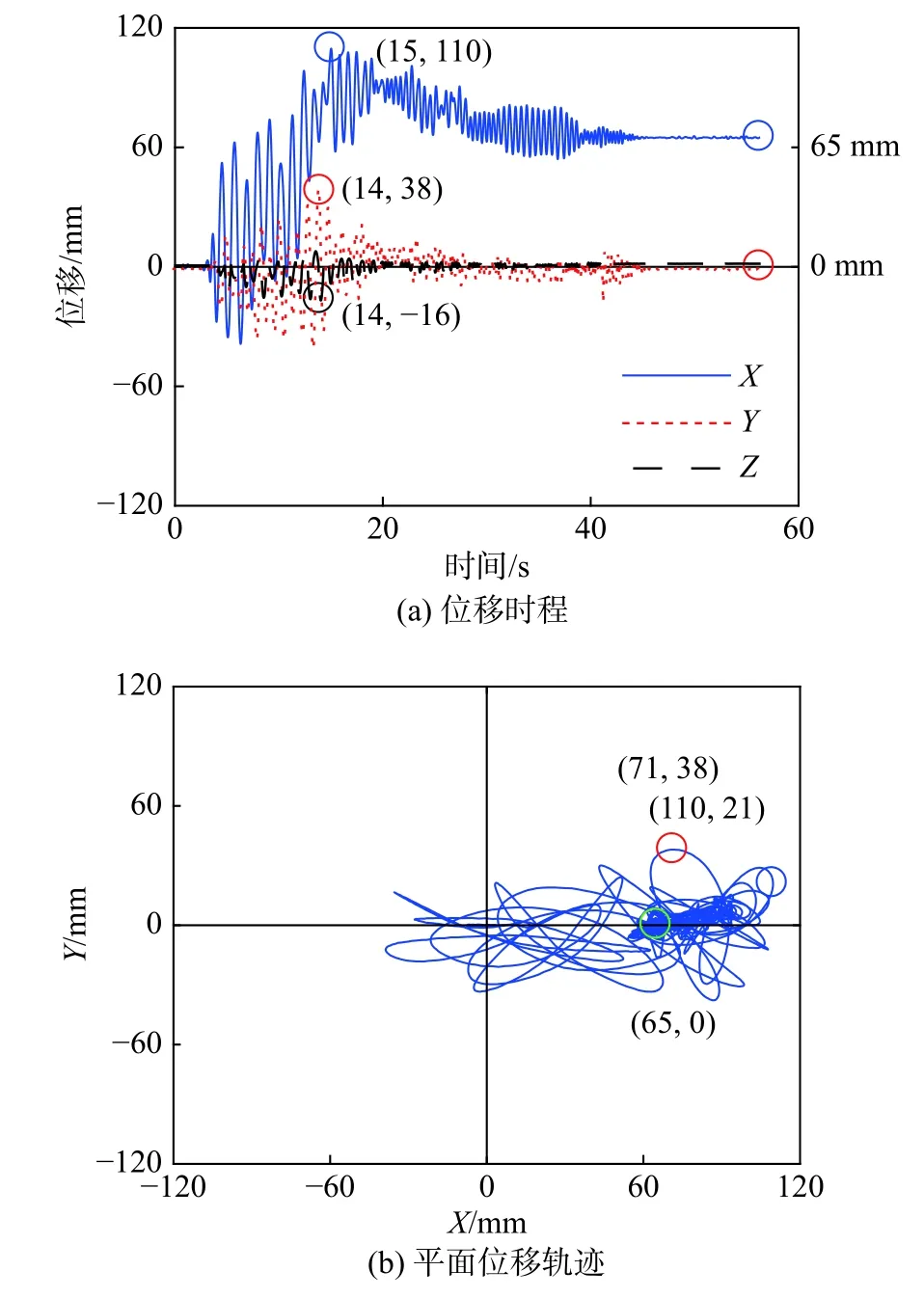
图13 El Centro (输入峰值0.35 g)Fig.13 El Centro (0.35 g)

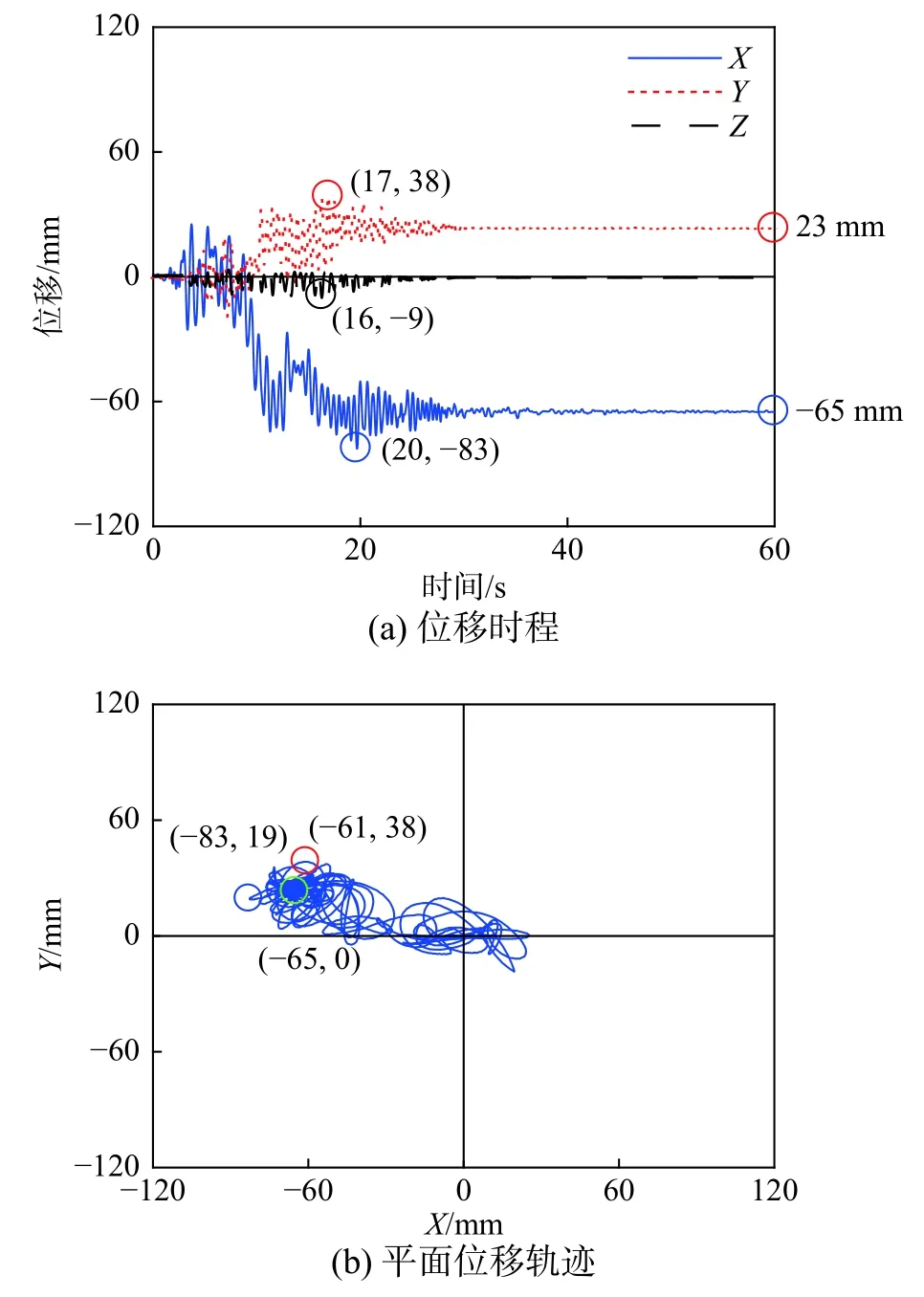
图14 Van Nuys (峰值0.58 g)Fig.14 Van Nuys (0.58 g)

在2 条人工波作用下的位移反应均大于2 条天然波形作用下的位移反应。AC156-ST 波作用下，两水平方向的位移反应较大，尤其是在Y 方向，位移峰值为85 mm，最终位移为60 mm，表明其扭转反应大于2 个天然波形作用下的结果(图15(a))。AC156-ST 波造成向左上方的平移量比Van Nuys波所造成的平移大很多(图15(b))。然而，由于其持续时间相对较短，位移峰值略小于El Centro 波作用下的位移。在AC156-LT 波作用下，相对滑移比其他三种波形更为明显。位移时程曲线面类似于正弦反应(图16(a))。对应的位移峰值(196 mm)大概出现在地震波输入接近尾声时，数值上几乎是AC156-ST 位移峰值的2 倍。从平面运动轨迹可以看出，花瓶的摆动方向倾向于X 轴一侧(图16(b))。持续长时间的输入致使花瓶的转角有所增加，从而加剧了倾覆破坏的可能性。每次试验后花瓶在竖直方向的最终位移和倾角均为零，说明每次试验后花瓶均回到了垂直摆放状态。

5.3 加速度反应

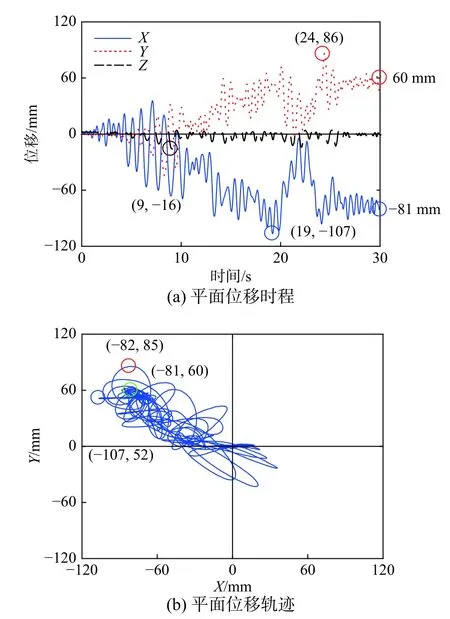
图15 AC156-ST (输入峰值0.6 g)Fig.15 AC156-ST (0.6 g)

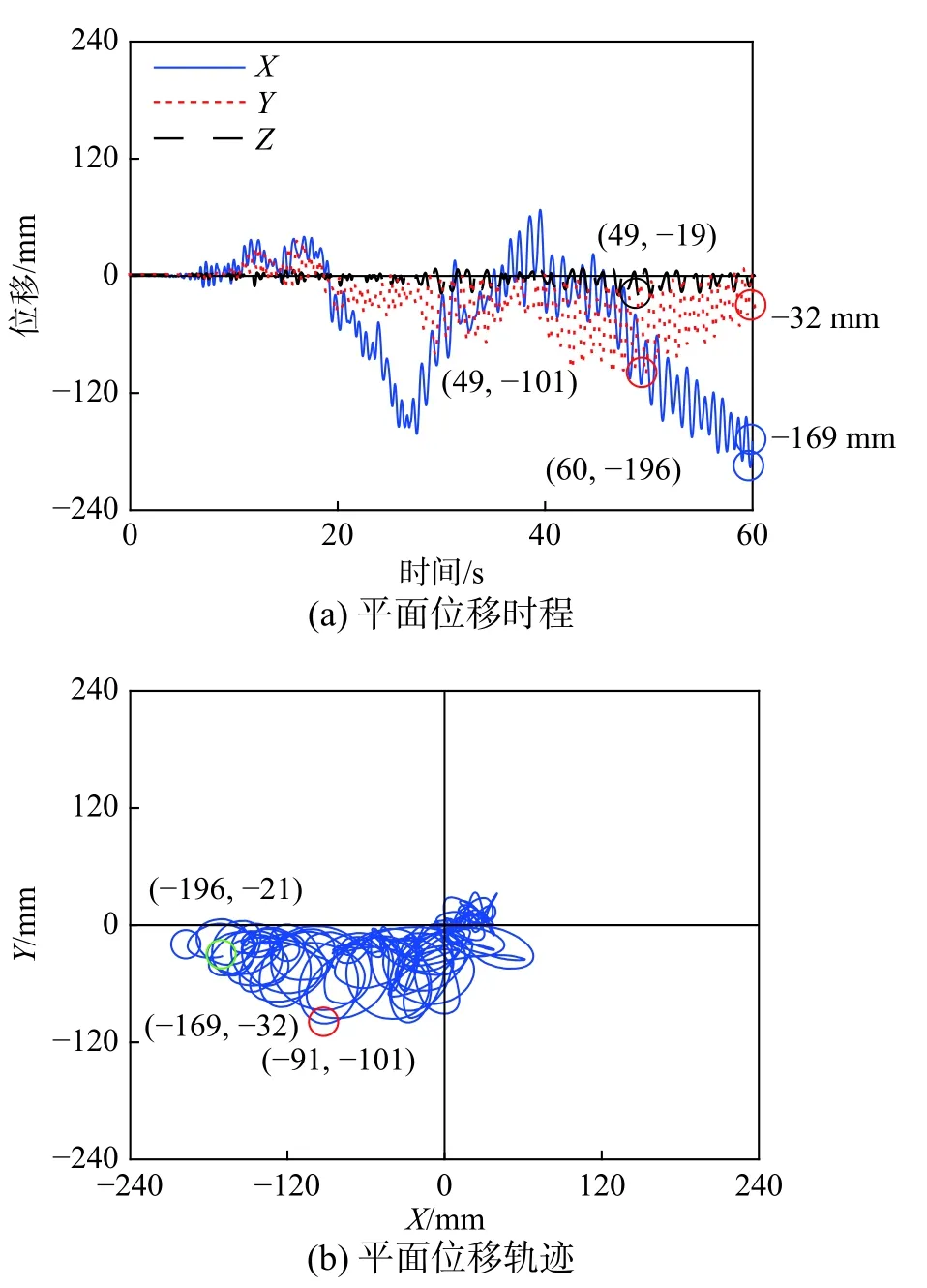
图16 AC156-LT (输入峰值0.6 g)Fig.16 AC156-LT (0.6 g)

对花瓶重心点的位移反应进行二次求导，可以得到对应的加速度反应，以此为基础可进一步研究花瓶底部摩擦力所产生的惯性力和花瓶的加速度传递能力，下文列出的均为点在XOZ 平面内的加速度时程曲线。加速度反应如图17～图20 所示。在El Centro 波作用下，当输入加速度峰值小于0.23 g(动摩擦系数)时，花瓶与地面之间没有相对位移(图17(a))，在Van Nuys 波(图18(a))、AC156-ST 波和AC156-LT 波作用下，也有类似现象发生。当输入峰值大于0.23 g 时，加速度反应峰值一般在0.23 g 附近，这一结果也出现在El Centro波(图17(b))、Van Nuys 波(图18(b))、AC156-ST 波(图19)和AC156-LT 波(图20)作用下的反应结果中，从侧面验证了1.1 节分析结果的合理性。由于滑移与摇摆组合模式的出现，再加上扭转反应的出现，使得一些加速度峰值大于0.23 g，如图17(b)、图18(b)、图19 和图20 所示，当然，也有可能是台面噪声造成的影响，可通过滤波确认和排除这一问题。在两条人工波作用下，加速度反应几乎在整个试验过程中都比较大，这可能是由于其频谱分量引起了花瓶与接触面的共振。总之，试验所得的加速度峰值与推拉试验得出的动摩擦系数的十分吻合，证明了动摩擦系数在浮放非结构物动力分析中起着关键的作用。因此动力反应模式(摇摆、滑移或滑移伴随摇摆)依赖于动摩擦系数，而不是静摩擦系数，这一结论对进一步分析和数值模拟均具有重要参考价值。

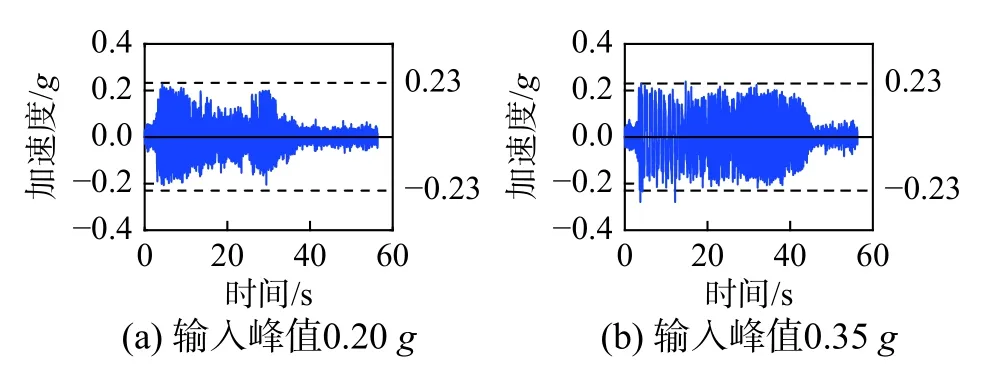
图17 加速度时程(El Centro)Fig.17 Acceleration response in El Centro

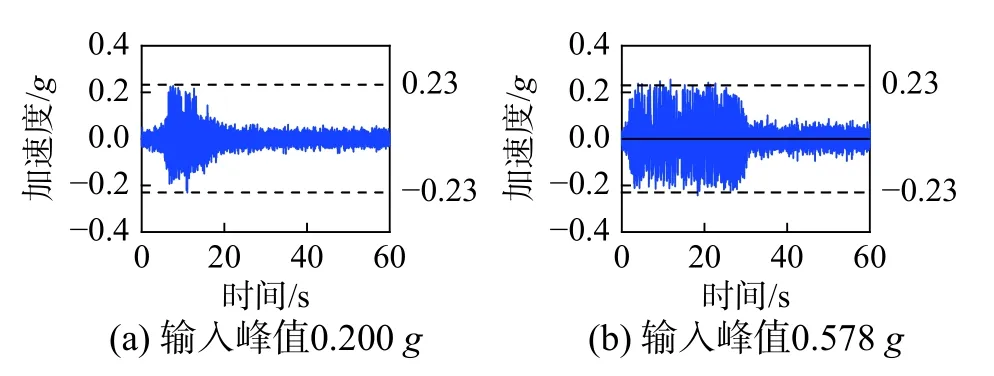
图18 加速度时程(Van Nuys)Fig.18 Acceleration response in Van Nuys

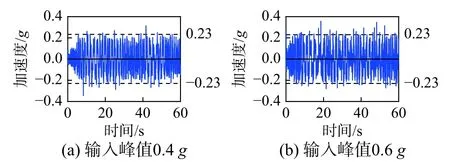
图19 加速度时程(AC156-ST)Fig.19 Acceleration response in AC156-ST

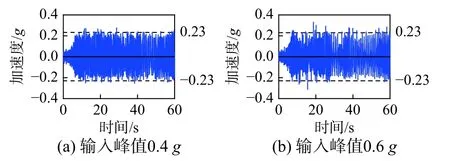
图20 加速度时程(AC156-LT)Fig.20 Acceleration response in AC156-LT

绝大多数浮放花瓶本身质量相对较小，地震破坏作用除了与建筑结构地震作用大小有关外，还与自身材质、自振频率等因素相关。相对于El Centro，人工波的频域更加接近于花瓶的自振频率(图10)，再加上更长的强震持续时间(图9)，导致人工波作用下的地震反应也明显高于El Centro。从图17、图19 和图20 可以看出，人工波作用下所观测到的强加速(峰值为0.2 g 左右)反应持续时间明显高于El Centro。

6 结论

将浮放非结构物简化为矩形刚体的物理模型已经被广泛认可并开展了大量的分析和研究工作[5 − 9]。在地震作用下，花瓶底部受到摩擦力作用，有4 种基本运动模式，即相对静止、相对滑移、摇摆以及摇摆伴随滑移，具体运动模式由花瓶自身尺寸、摩擦系数和支承面地震动波形特性共同决定。通过对浮放花瓶开展摩擦系数试验和振动台试验，得出以下主要结论：

(1) 花瓶的运动模式依赖于输入的加速度峰值，加速度峰值越大，动力反应越剧烈；

(2) 动力反应随不同输入波形的激励而变化，表明输入波形的持续时间、频谱分量等也影响着动力反应的大小；

(3) 对于摩擦系数，推拉试验结果与振动台试验结果非常吻合，进一步证明了两次试验结果的可靠性；

(4) 花瓶的运动模式也得到了验证，具体的运动模式与动摩擦系数密切相关，验证了分析结果的可靠性；

(5) 花瓶的几何形状看起来是轴对称的，但试验中发生了扭转运动，说明花瓶的质心和形心并不重合，这一现象可能存在于大量的复杂浮放非结构物。

在今后的研究中，应进一步研究浮放花瓶的失效模式、性能水平和易损性分析，并从文物保护的角度出发，进一步探讨减、隔震的措施，从而减少或避免其在强震作用下的破坏。