一类几何题的解法探讨

任东升

在教学中，我发现一类几何题教师难教，学生难学，而这类题细嚼起来是有规律可寻的

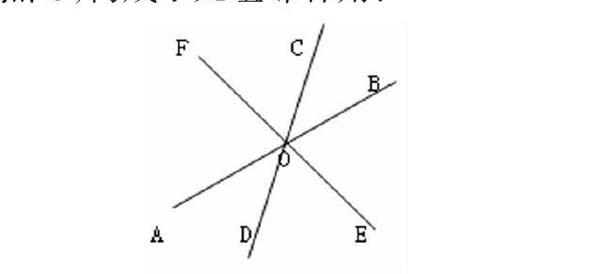
比如：三条直线相交于一点O，构成了几组邻补角？

分析：这个题看起来很简单，但细细算起来学生很容易出现多数或漏数的现象。

我发现这类题应该从其概念入手：邻补角是指两个角，且这两个角在大小和位置上都有特殊的要求，就是它們有一条公共边，另一条边在同一条直线上有共同的顶点且方向相反，此时就出现了特殊的图形。

一条直线和从这条直线上发出的射线，这样就是一对邻补角∠1和∠2。

有了这样的一个前提，我们就可以准确的找出三条相交直线构成的邻补角对数，以AB为直线OF.OC.OD.OE为射线就有4对邻补角.又以CD为直线OA.OB.OE.OF为射线又有4对…再以EF为直线OA.OB.OD.OC为射线….

由此类推即可得出准确的邻补角的对数.

再如：n条直线两两相交最多把平面分成了几部分（n≥1）？

分析：1条直线把平面分成两部分;2条直线把平面分成4部分;3条直线相交把平面分成了7部分……

再增加一条直线，它经过原来的7个部分中的4个部分，即增加了4个部分，就可把平面成11个部分.继续增加直线，它会经过原来的11个部分中的5个部分…….

归纳起来

此类几何问题在数学教学中有很多.我们可以在其中寻找规律，发现数学的美.让学生在愉悦中探求知识的真谛.