基于BP神经网络模型的住宅用地地价评估研究——以南昌市主城区为例

陈志鹏，郭 熙，赵丽红*，郭细根

(1.江西农业大学国土资源与环境学院，330045，南昌；2.重庆理工大学经济金融学院，400054，重庆)

0 引言

改革开放以来，我国土地交易市场的建设取得重大突破。从土地公开市场的土地出让收益来看：1999—2015年，这17 a全国土地出让收入总额为37 457亿元，2017年这一数据猛增至52 059亿元[1]。由此可见，我国土地出让市场呈现异常活跃、交易量大的特点。为了规范土地交易市场，抑制土地价格的不合理增长，对土地估价的精度要求也越来越高，提高地价评估的客观性和科学性很有必要。在此背景下很多学者基于不同视觉、采用不同的技术方法对地价评估进行研究，如回归模型[2]、模糊数学[3]、云模型[4]、克里金插值[5]等方法。但上述方法均未考虑地价影响因素权值确定这一主观性问题。随着人工智能的兴起，不少学者将人工智能方法运用于地价评估，如BP神经网络，支持向量机[6]和随机森林[7]等方法。该些方法均规避了地价影响因素的权重问题，建立地价与其影响因素间的映射关系，更具有一定的客观性与优越性。

与传统估价方法中的市场比较法相比，BP神经网络有很多相似之处，但是与市场比较法不同的是，神经网络不需要人为地确定修正系数，这也就在很大程度上降低了人为因素对估价的影响。因此为减少在土地估价过程中人为主观性，提高估价科学性，本文将BP神经网络引入到住宅地价评估中，采集南昌市主城区100多个住宅土地交易案例，探讨适用于南昌市主城区住宅用地的地价评估自动机制。

1 基于BP神经网络模型算法的地价评估模型

1.1 BP神经网络算法原理

在整个人工神经网络当中，BP神经网络是精华部分，处于核心地位，广泛用于回归、逼近、压缩、识别等领域。在实际应用中，大约80%的神经网络模型采取了BP网络或BP网络的变化形式。BP网络大体上由输入层、隐含层和输出层组成，其中隐含层可以分为一层或者多层[8]，如图1所示，该图是一个简单的神经网络结构示意图，该神经网络包含有1个输入层、2个隐含层、1个输出层。

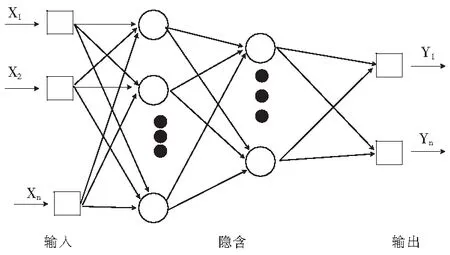
图1 BP神经网络结构

BP神经网络的学习过程由两部分组成：正向传播和反向传播[9]。把量化的影响因子作为输入层，在隐含层，网络会自动地在地价与影响因子之间建立非线性映射关系，赋予每个影响因子以一定的初始权重和偏置(即阈值)，然后正向地传播过去，发现得出的结果与给定的结果之间存在较大的误差，那么网络就会沿着使误差递减速度最快的方向反向传播，修正权重和偏置，这个过程称为1次迭代，这个递减速度也叫做学习率。循环往复，经过多次迭代，直到得到的误差小于期望误差，至此，训练结束。

1.2 BP神经网络地价评估模型

BP神经网络地价评估原理是建立地价及其影响因素非线性映射关系，并通过全局优化功能去获取 BP 神经网络最优的初始权值和阈值， 将这些参数代入网络，然后用仿真模拟函数进行地价的模拟和预测[10]。

图2 BP神经网络地价评估原理

2 实证研究

2.1 研究区概况、数据来源与处理

本文以南昌市中心城区建成区为研究区(依据城市总体规划确定的城市建成区)。南昌市为江西省的省会城市，占地面积7 401 km2，地处江西中部偏北，赣江下游，鄱阳湖的西南岸，位于东经E115°27′～116°35′、北纬N28°10′～29°11′之间。全境山、丘、平原相间，地形主要以平原为主，占总面积35.8%，东南相对平坦，西北丘陵起伏，水网密布，湖泊众多。2018年，南昌市全年实现地区生产总值(GDP)5 274.67亿元，比上年增长8.9%。其中，第一产业产值190.68亿元，增长3.2%；第二产业产值2 660.92亿元，增长8.5%；第三产业产值2 423.07亿元，增长10.1%。

本文用于地价评估的样本数据为2016年南昌市城区基准地价评估所采用土地交易案例，从中选取了103个住宅用地交易案例作为样本点，包括样本点的容积率、交易价格等信息。在中国地价监测网获取不同时期南昌市住宅用地的地价水平值，以2019年3月1号为评估基准日，将地价修正到评估基准日。住宅地价样本点分布如图3所示，样本点较为均匀地分布在南昌市主城区内。本文随机选取了90个样本作为训练样本集，占样本总数的87%，其余13个样本作为测试样本集，占样本总数的13%。

图3 样本点分布图

2.2 住宅地价影响因素体系构建与量化

在选取影响因子时，参考南昌市城市土地定级因素因子指标体系。1)在影响地价的商业因素中选取了商服中心作为影响因子；2)在影响地价的交通因素中，选取了客运站、主要道路、普通道路、公交站点作为影响因子；3)在影响地价的基础设施因素中选取了小学、初中、幼儿园、医院作为影响因子；4)在影响地价的环境因素中，选取了公园作为影响因子。影响因子表见表1。

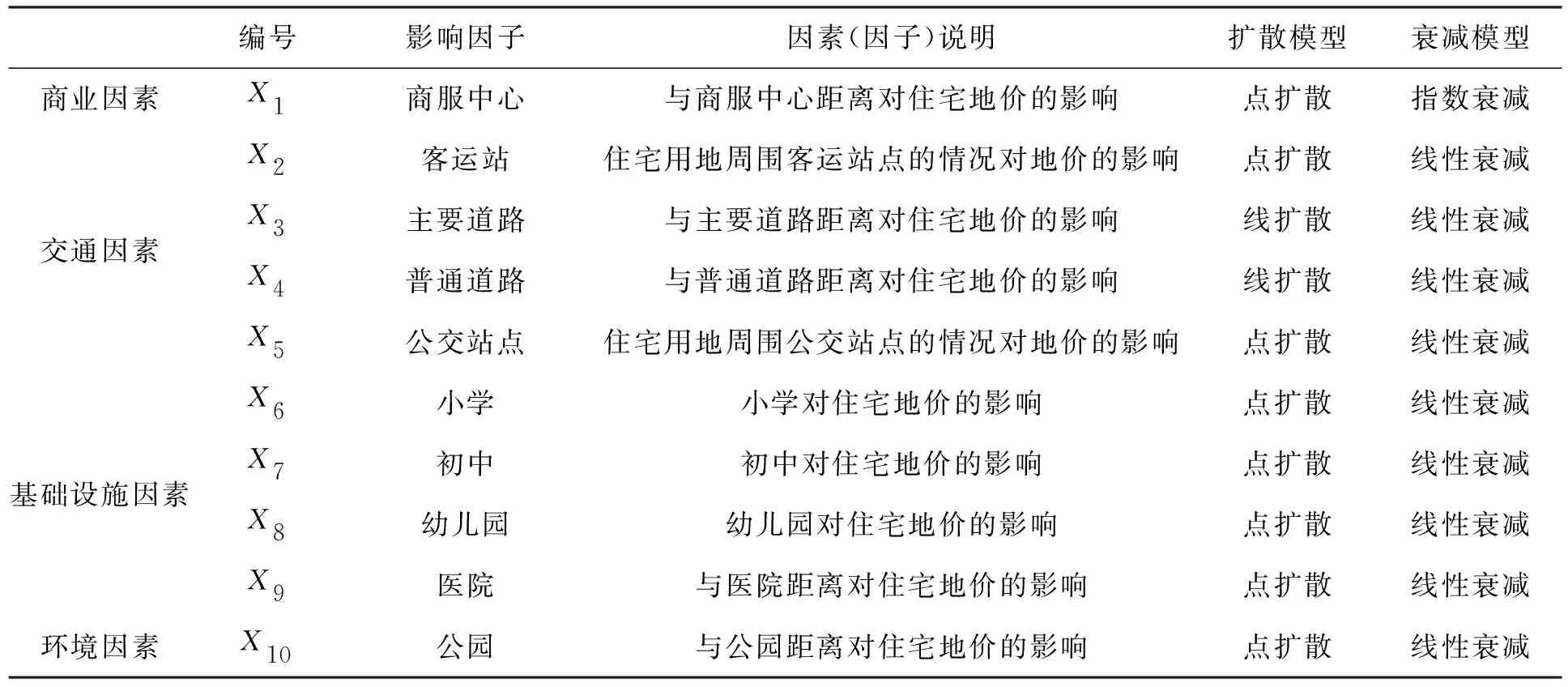
表1 住宅地价影响因素(因子)表

基础设施点状数据通过POI获取，小学、公交站点、客运站(无坐标信息)利用地理编码获取经纬坐标，再将所获取的点状要素进行投影转换为西安80坐标系。

对影响因子的量化，根据衰减模型进行分值计算。运用ArcGIS空间分析中的欧式距离和栅格计算器进行因子量化，再把计算出来的值赋予到每个样本点上。量化分值范围为0～100分，分值越高，土地价格的理论值越高。结果如图4所示。

图4 各影响因子功能分值图

2.3 相关分析和灰色关联度分析

为了减小变量间的多重共线性对模型的影响，现对影响因子进行相关分析，求出影响因子两两间的相关系数，发现公交站点与7个影响因子显著相关，公园与6个影响因子显著相关，商服中心与其他6个影响因子显著相关，幼儿园与6个影响因子显著相关，那么剔除掉这4个影响因子。

对剩下的7个影响因子进行灰色关联度分析，检验其与地价的关联度大小。灰色关联度是一种衡量因素间关联程度的方法，它是根据序列曲线形状与参考序列的曲线形状的相似程度来计算关联度大小的。计算步骤如下。

1)确定比较序列和参考序列，{X1(k)}、{X2(k)}、{X3(k)}、{X4(k)}、{X5(k)}、{X6(k)}、{X7(k)}作为比较序列，{X8(k)}作为参考序列。其中X1为初中，X2为客运站，X3为普通道路，X4为小学，X5为医院，X6为主要道路，X7为容积率，X8为修正后地价。

2)数据的无量纲化处理。利用平均值标准化的方法，公式如下：

(1)

计算灰色关联度。公式如下：

(2)

ζi(k)为灰色关联系数，ρ为分辨系数，一般取值为0.5，得到灰色关联度的值为：

(3)

以上过程在DPS 9.01中实现，得到关联矩阵，其中G(8,1)=0.741 3、G(8,2)=0.749 60、G(8,3)=0.751 29、G(8,4)=0.770 46、G(8,5)=0.749 93、G(8,6)=0.761 17、G(8,7)=0.755 71，关联序：X4>X6>X7>X3>X5>X2>X1。可见，7个影响因子与地价的关联程度均大于0.7，对地价的影响力大，可以作为模型的解释变量。

2.4 模型构建

2.4.1 训练样本准备 经过量化后的样本数据，一部分要用来对BP神经网络模型进行学习与训练、从而得到合格的评估模型，另一部分要用来检测该模型的准确性与可靠性[12]。将每个住宅样点在各影响因子下的量化分值作为输入变量，输出变量为经过时间修正后的住宅用地交易价格。

2.4.2 网络结构及参数的确定

1)网络层数的确定。本文选取了7个影响因子作为输入变量，故输入层节点数为7个，地价作为输出变量，故输出层节点数为1个；至于隐含层，一般来说，层数越多、节点越多，训练模型上的效果越好，甚至会达到100%预期精度。但随之带来的问题是过拟合，将模型放在预测数据上的效果严重降低，而且训练时间也会延长。因此，隐含层数设置为1层，根据节点公式：

(4)

式中：∝为1～10之间的常数、n为输入层节点数、m为隐含层节点数，因此，确定隐含层节点数为8个[13]。在输入层与隐含层之间选择tansig函数为传递函数，在隐含层与输出层之间选择函数purelin作为传递函数。最终构建的网络为“7-8-1”的3层网络结构。

2)期望误差的确定。在对神经网络训练前，需要设置一个期望误差，期望误差既不能设置得过小、也不能设置得过大。期望误差过大，会降低预测精度；期望误差过小，会导致网络还没有达到期望误差就停止训练。根据经验值及多次训练结果的比较，最终确定期望误差为0.001。

3)学习率的确定。在逆向传播的过程中，BP神经网络采用的是随机梯度下降算法去调整权值和偏置(即阈值)来减小误差。梯度下降法需要设置学习率，学习率决定了一个小批量中权重在梯度方向要移动多远。如果学习率过低，尽管训练会变得更加可靠，但是朝向损失函数最小值的每个步长很小导致优化会耗费较长的时间。如果学习率过高，情况可能会更糟糕，因为训练可能不会收敛，甚至会发散，权重的改变量非常大，使得优化越过最小值，损失函数变得更糟[14]。权重用公式表示为：

(5)

式中：α为学习率，θi为权重值，j(θi)为损失函数。学习率过小(左)和学习率过大(右)对损失函数的影响如图9所示。综合分析，最终确定学习率为0.1。

图5 权重变化与损失函数的关系

4)最大训练迭代次数。在网络训练结束前，为了让最后的误差小于期望误差，设置最大的训练迭代次数为10 000次。

2.5 网络运行与预测结果

在进行BP神经网络预测时用Matlab语言对BP网络进行仿真训练。Matlab工具箱中包含了神经网络工具箱，为神经网络的构建、训练、模拟、仿真模拟提供了很多函数，这样的话，人们在使用这些函数时就不需要编写复杂而庞大的算法程序，人们可以根据自己的需要调用相关的程序[15]。

从图6可以很清楚地看到，模型在147次迭代以后输出的误差达到了设定的精度，在这个过程中所花费的时间也很短，仅为数秒钟。训练误差下降很快，在50次以内下降得尤其明显，且从回归图来看，线性拟合效果很好，说明网络的学习状态良好。利用仿真模拟sim函数预测后面20组样本的地价，用sim函数预测出来的值是归一化的值，再经过反归一化得到土地价格。预测结果如图7所示，预测误差统计结果见表2。

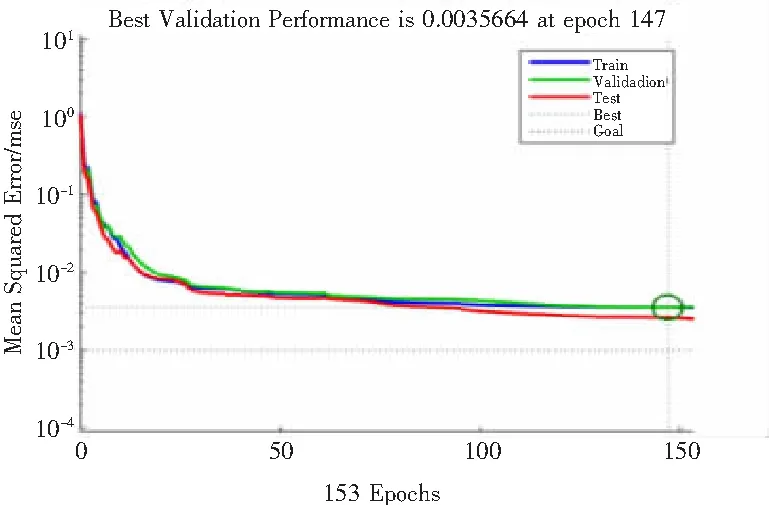
图6 误差变化图与回归图

图7 预测输出(上为BP网络，下为SVM模型)

在用BP神经网络对地价进行评估的同时，作为对比，也用支持向量机模型(简称SVM模型)对地价进行评估。得到的误差变化图与回归图以及验证样本表如下所示：可以看出，无论是BP神经网络还是SVM模型，得到的预测值与实际值的拟合优度都很高，预测值与实际值的误差百分比也在合理范围之内，没有偏差太大，只有个别点的误差偏大一些，是由于该样本点的选取不够合理所致，因为对于该样本点的预测，无论是BP神经网络还是SVM模型，都出现较大误差。总的来说，BP神经网络对地价的预测是比较精确的。

表2 验证样本表

值得一提的是，尽管SVM模型给出的预测值的误差要小于BP神经网络，但是SVM模型在整个运行过程中用了数分钟才完成，而BP神经网络只用了数秒钟。BP神经网络的运行效率要远远高于SVM模型，SVM模型对计算机的运算性能有更高的要求。综合预测精度跟运算性能两者来考虑的话，BP神经网络要好一些。

3 结论与讨论

本文以南昌市主城区的住宅地价作为研究对象，根据影响地价的主要因素，选取了商服中心、客运站、主要道路、普通道路、公交站点、小学、初中、幼儿园、医院、公园等作为影响因子，再获取量化分值。经过相关分析和灰色关联度分析，剔除掉了公交站点、公园、商服中心、幼儿园4个影响因子。用前83组样本进行训练，找出最优权重和阈值，再用仿真模拟函数对剩下的20组样本进行预测。结果显示预测值与实际值的误差控制在合理范围以内，表明BP神经网络模型进行地价预测是可行的，且预测精度较高。

BP神经网络有着强大的非线性映射能力，能够在影响因素与地价之间迅速建立起一种联系。跟传统估价方法中的市场比较法相比，BP神经网络有很多相似之处，不同的是，BP神经网络不需要人为确定修正系数，这也就在很大程度上降低了人为因素对估价的影响，使得估价的过程更加符合评估的三大原则：独立、客观、公正。

用神经网络对地价进行评估仍存在两大缺陷：一是用BP网络进行评估时，要选取具体的、可以量化的影响因子。也就是说，神经网络只能进行定量分析。但是在影响地价的因素当中，有些只能进行定性分析，如国家宏观政策对地价的影响；二是用BP网络评估地价从本质上来说，与市场比较法是一致的。训练样本即为可比交易案例，根据可比交易案例的情况，来预测待估宗地地价。因此，市场法适用的BP网络也适用，市场法的局限性也是BP网络的局限性。对于划拨出让、协议出让或者市场不活跃的土地价格的确定，BP神经网络不适用，因其交易价格无法获取。即便如此，对于南昌市城区住宅用地地价评估来说，BP神经网络是适用的。

随着智能化时代的到来，类似于BP神经网络的人工智能方法将会应用到各行各业中，将BP神经网络应用到土地估价当中，也会推动我国土地估价工作的发展，为政府和经济主体参与经济活动提供科学的依据。