基于灰色-马尔柯夫模型的心血管病死亡率预测研究

王梓宽，于海雯

(1. 南昌大学前湖学院，330031，南昌；2. 南昌大学信息工程学院，330031，南昌)

0 引言

随着社会与经济的发展，人们的生活水平和生活方式发生了深刻变化。人口老龄化及城镇化的加速等，心血管病危险因素流行趋势越发明显，导致了心血管病的发病人数持续增加，且今后10 a心血管病患病人数仍将继续增长[1]。根据2019年中国卫生健康统计年鉴[2]中的数据，心血管病(心脏病、脑血管病)死亡占城乡居民总死亡原因的首位，2018年心血管病农村死亡率为322.31/(10万)，其中心脏病死亡率为162.12/(10万)，脑血管病死亡率为160.19/(10万)；城市心血管病死亡率为275.22/(10万)，其中心脏病死亡率为146.34/(10万)，脑血管病死亡率为128.88/(10万)；2018年农村、城市心血管病死亡占全部死因的比率分别为46.66%和43.8%。心血管病事件的发生主要归因于血压和总胆固醇水平升高等原因，在1958—1959年、1979—1980年、1991年、2002年进行过4次全国范围内的高血压抽样调查[3]，≥15岁人群高血压的患病粗率分别为5.1%、7.7%、13.6%、17.6%，总体呈上升趋势。心血管病的疾病负担日渐加重，已成为重大的公共卫生问题[1]。能否较准确地预测心血管病死亡率，有利于指导预防心血管病事件的发生和公共卫生事业的可持续发展。因此研究心血管死亡率的预测方法对引导我国公共卫生事业的健康发展是非常有意义的。

灰色预测理论的核心和基础是GM(1,1)模型[4-6]，它适用于时间短、数据少、波动小、具有长期趋势的预测对象。对随机波动较大的对象，其预测值就会出现偏高或者偏低，拟合程度较差。马尔柯夫预测模型则适合于一个随机变化的动态系统，根据状态间的转移概率来预测系统未来发展趋势。目前不少研究者把灰色GM(1,1)模型与马尔柯夫预测模型相结合[7-10]，即灰色-马尔柯夫预测模型。本文主要研究灰色-马尔柯夫的心血管病死亡率预测模型，提出了一种改进的灰色-马尔柯夫预测模型，并利用1991—2018年统计数据[2,11]进行数值模拟。数值模拟结果表明本文提出的改进的灰色-马尔柯夫预测模型是有效的。

1 灰色-马尔柯夫预测模型

1.1 灰色GM(1,1)模型

GM(1,1)模型是最简单的灰色动态预测模型[4-6]，它的建模原理及过程如下所述。

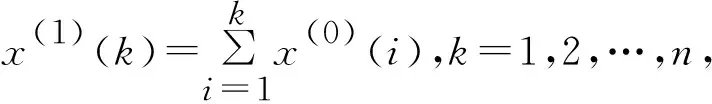
(1)

其中a和u是需由x(1)来确定的参数。对式(1)中的方程两边在[k,k+1]上积分得

(2)

显然，x(1)(k+1)-x(1)(k)=x(0)(k+1)，于是式(2)等价为

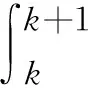
(3)

当k取从1到n-1时，则得超定方程组

(4)

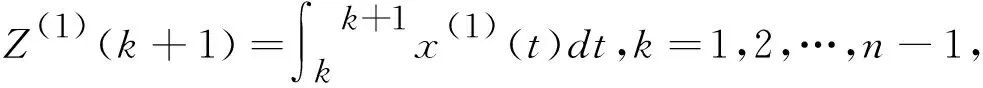
(5)

于是，得到GM(1,1)预测模型为

(6)

1.2 马尔柯夫预测模型

设{Yn,n=0,1,2,…}是一个离散型随机变量序列，且Yn所可能取值属于E，而E是个包含有限个元素的集合,在此即为有限个状态的集合。如果Yn+1的条件概率只依赖于Yn的值，即P(Yn+1=in+1|Yn=in，Yn-1=in-1,…,Y0=i0)=P(Yn+1=in+1|Yn=in)，则称该随机过程是个有限状态的马尔柯夫链[7-8]。在描述马尔柯夫链的概率分布时，最重要的是条件概率pij(k)=P(Yk+1=j|Yk=i)，它表示在时刻k时Yk取i值的条件下，在下一时刻Yk+1取j值的概率，一般称pij(k)为k时刻的一步转移概率。若随机变量从i状态转移到j状态的条件概率与时刻k无关，即pij(k)=P(Yk+1=j|Yk=i)pij，则称其为齐次马尔柯夫链。

设P为齐次马尔柯夫链的一步转移概率pij的矩阵，即

(7)

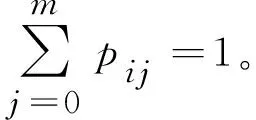
1.3 灰色-马尔柯夫预测模型

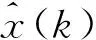
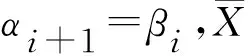
(8)

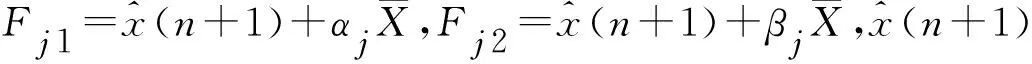
1.4 改进的灰色-马尔柯夫预测模型

为进一步提高预测精度，本文提出以下改进的灰色-马尔柯夫预测模型，即取

(9)

为x(0)(k)的新拟合值和预测值，其中β0,β1,β2,β3,β4,β5为待定参数。在下面对心血管病死亡率的预测中，利用MATLAB软件中函数regress直接计算出β0,β1,β2,β3,β4,β5，使用格式为：

b= regress(y,A,alpha)，

其中y为原始数据x(0)(k)，A为对应于回归系数β0,β1,β2,β3,β4,β5的矩阵，alpha为置信水平α(缺省时α=0.05)；输出b是一个六维列向量，它的分量分别是β0,β1,β2,β3,β4,β5的计算值。

1.5 状态划分的计算方法

为给出灰色-马尔柯夫预测模型中状态划分，先给出中心趋势曲线的定义。

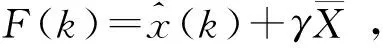
成立，则称F(k)为原始数据的中心趋势曲线。

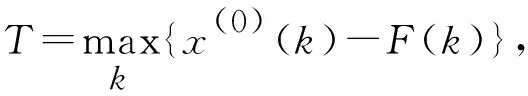
2 心血管病死亡率的灰色-马尔柯夫预测

本文分别选取1991—2018年农村与城市心血管死亡率[2,11]作为预测对象，其中1991—2016年的数据作为原始数据来建立灰色-马尔柯夫链预测模型，2017年、2018年的数据作为预测样本数据，从而观察预测效果。

首先，在方程组(4)中代入1991—2016年的数据，求得方程组(4)的最小二乘解。于是，得到农村、城市心血管病死亡率的灰色GM(1,1)预测模型分别为：

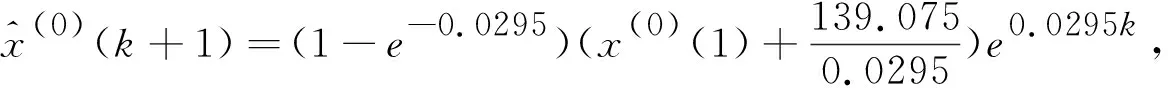
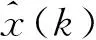
改进的灰色-马尔柯夫模型的预测效果见图1，其与GM(1,1)模型预测的对比以及精度检验见表1。

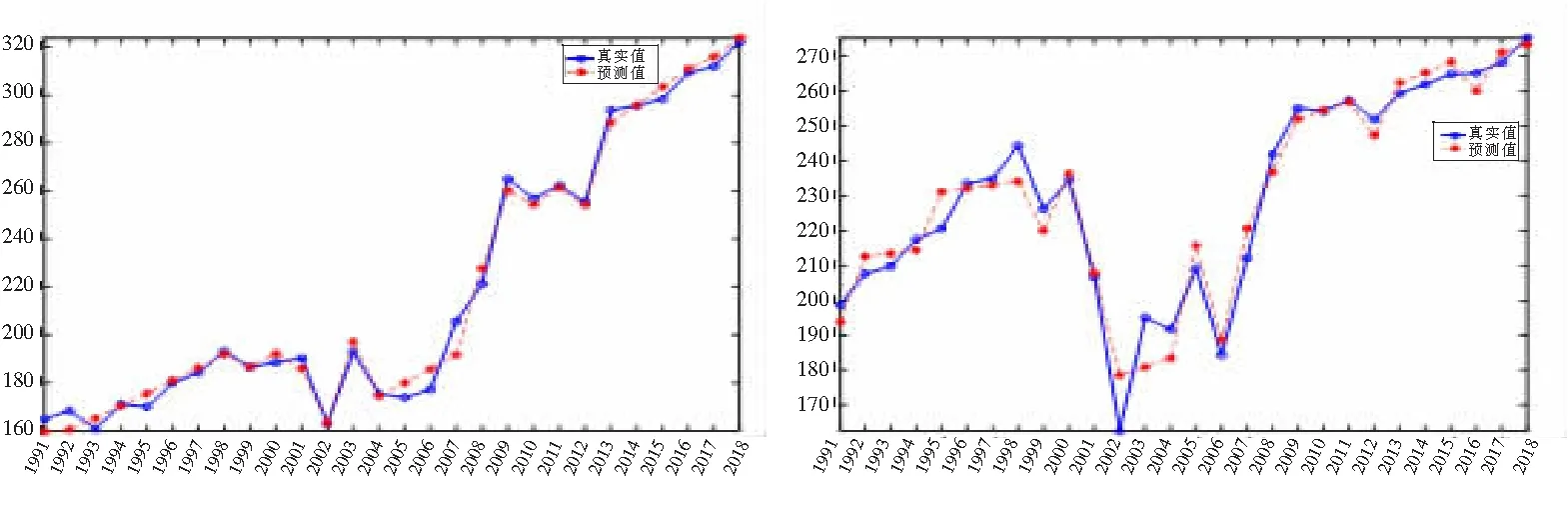
(a)农村心血管病死亡率 (b)城市心血管病死亡率

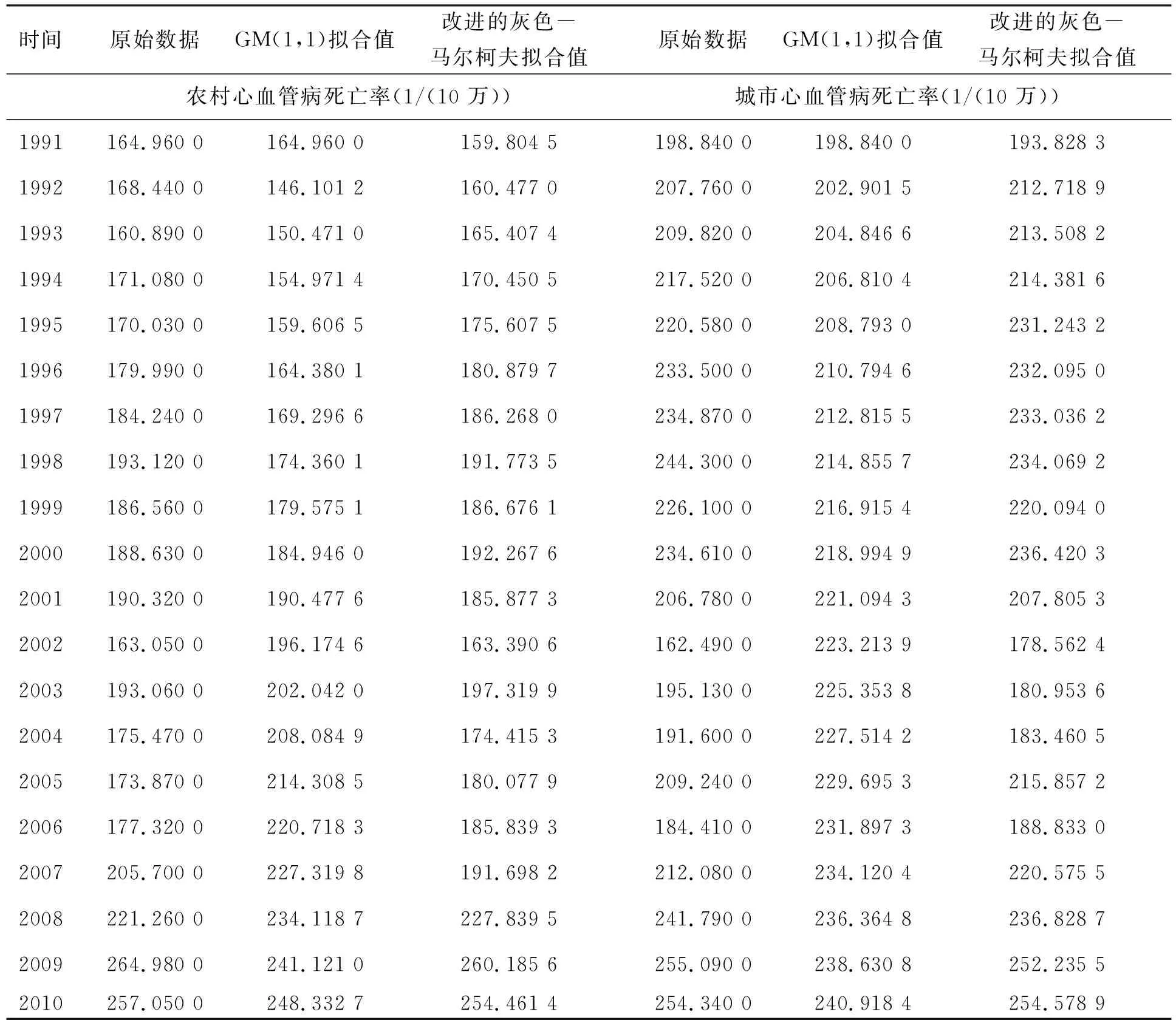
表1 改进的灰色-马尔柯夫模型与GM(1,1)模型拟合结果以及精度检验

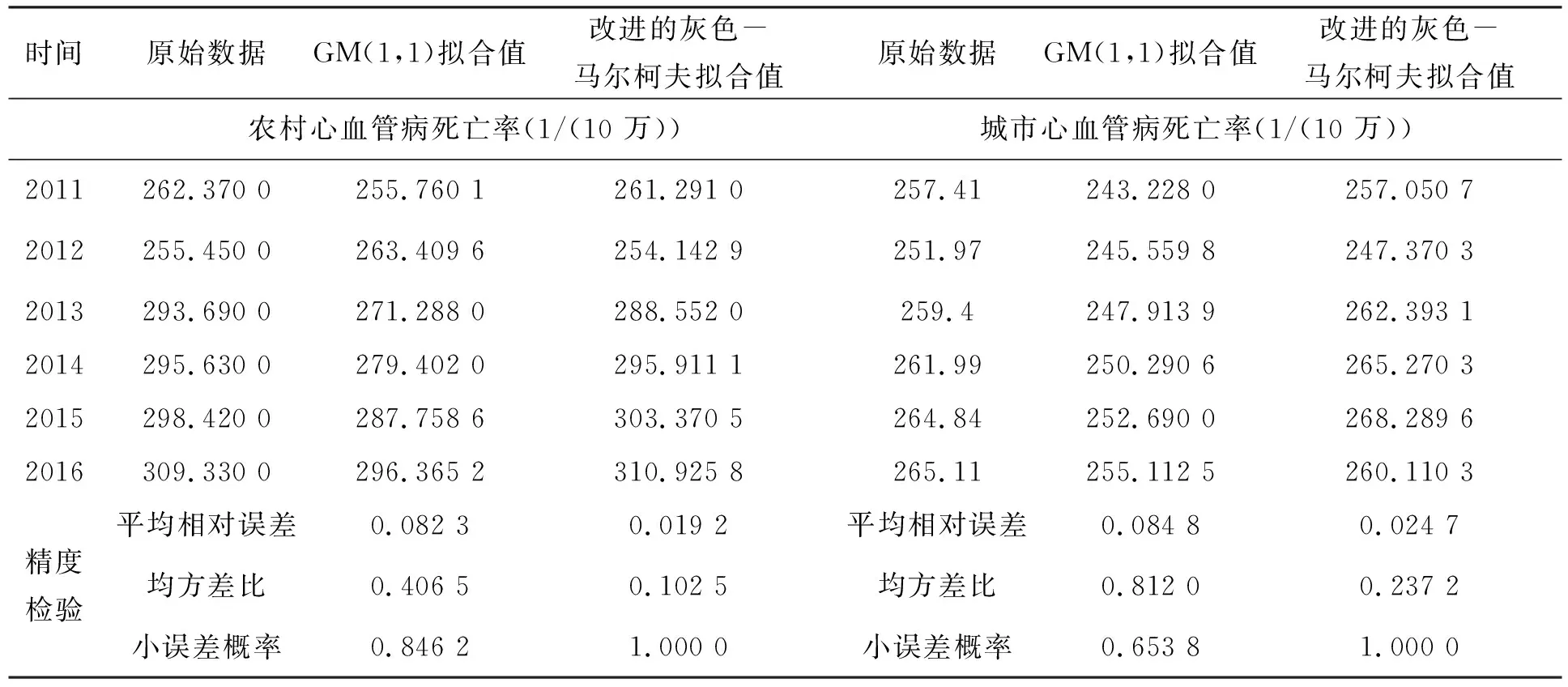
表1 (续)

根据表2[5]中的精度检验分级标准及表1、表3中的计算结果，可知本文提出的改进的灰色-马尔柯夫与模型能很好地对心血管病死亡率进行预测，且对农村心血管病死亡率的预测具有更好的结果，其中原因可能是城市心血管病死亡率在2002年较其他年份非常低而导致模型的精度偏弱。

表2 精度检验分级标准

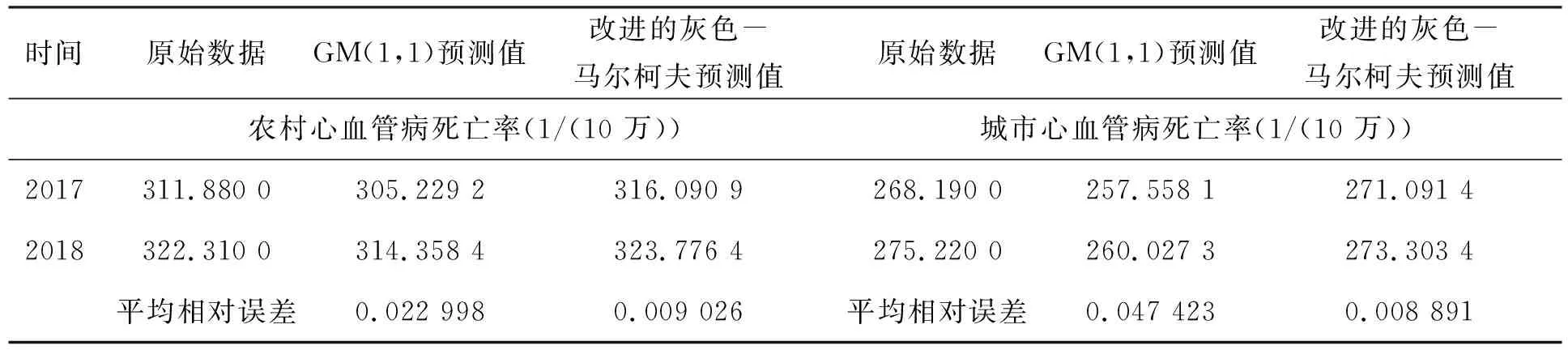
表3 改进的灰色-马尔柯夫模型与GM(1,1)模型预测结果

3 结论

本文针对1991-2018年农村与城市心血管病死亡率的统计数据，选用灰色-马尔柯夫模型来对其进行预测，提出了一种改进的灰色-马尔柯夫心血管病死亡率预测模型，数值模拟结果表明改进的灰色-马尔柯夫预测模型是有效的，特别是对当前农村心血管病死亡率的预测，这将有利于预防和指导心血管病防治公共卫生事业的发展。实际上，心血管病与高血压、血脂异常、空气污染等许多因素有关，如何建立心血管病事件与重要因素之间因果关系，从而建立更好的预测模型是需要继续深入研究的。