管内水流和地铁振动耦合作用下埋地供水管道的振动响应分析

李显昌 朱海涛 ，2，*

（1.天津大学建筑工程学院土木工程系，天津300072；2.滨海土木工程结构与安全教育部重点实验室（天津大学），天津300072）

0 引 言

供水管道作为城市的“生命线”，其一旦遭到破坏将严重影响城市的正常运转，甚至危害市民的生命安全。埋地供水管道运行环境十分复杂，诱发管道事故的因素很多，例如断层、不均匀沉降、震害、温度、腐蚀、老化等［1］。随着近些年地铁的大规模建设，地下空间变得日益狭窄，隧道和管线交叉邻近现象也日愈常见。地铁在运行过程中产生振动，振动以波的形式通过道床传递给隧道支护，支护结构再通过周围岩土介质向外传播，进而诱发埋地供水管道振动，对其运行安全造成影响［2-3］。

实事上，类似问题已经引起了一些相关人员的关注。朱学仁等［4］通过监测列车通过杭州市区某铁路桥时，桥墩振动引起临近几十厘米处的天然气管道的振动响应，并用监测数据结合相关规范对管道安全进行理论计算，得出管道安全运行结论，但这项研究主要针对地上架空管道，其研究成果不适用于埋地管道；吴昭华［5］针对东莞至惠州城际轨道交通项目在运营过程中对下穿新奥燃气管道可能会造成的影响，建立了轨道、隧道结构、土体和管道的三维有限元模型，并采用最不利工况对其进行了分析，对燃气管道正常运行安全进行了评估，但该项研究针对燃气管道，不适用于供水管道，且在研究中只考虑了交通振动的影响，并未考虑管道内部燃气对管道的影响，即流固耦合作用。供水管道与天然气管道有较大区别，所以以上针对天然气管道在轨道交通振动作用下的振动响应及研究无法为类似供水管道在轨道交通作用下振动响应提供参考。

目前尚未见到直接针对地铁振动作用下供水管道振动响应深入研究的公开报道，因此本文采用数值模拟方法，考虑流固耦合作用和地铁振动作用，得出供水管道的振动响应规律，以期为今后供水管线设计和安全评估提供一些参考。

1 车辆振动荷载

潘昌实［6-7］等把列车的动荷载用一个反映低、中、高频振动特征、附加动载和钢轨面波磨效应的激振力函数来模拟，其经验公式为

式中：P0为车轮静载；ω1、ω2、ω3为钢轨振动圆频率；P1、P2、P3分别对应于表1中Ⅰ、Ⅱ、Ⅲ控制条件下某一典型矢高值ai所对应钢轨振动荷载幅值。

振动荷载幅值为：

式中：M0为车辆簧下质量；ωi为相应车速下对应于表1 中Ⅰ、Ⅱ、Ⅲ控制条件下不平顺振动波长下的圆频率。

式中：V为列车的运行速度；Li为相应车速下对应于表1中Ⅰ、Ⅱ、Ⅲ控制条件下不平顺振动波长。

表1 英国轨道几何不平顺几何参数Table 1 Geometric parameters of British or bital irregularity

地铁型号采用文献［8-9］中的参数，取单边静轮重P0为8×103kg；簧下质量为750 kg；不平顺波长和相应的矢高分别取L1=50和a1=16、L2=5和a2=2.5、L3=0.5和a3=0.1。

根据以上公式使用MATLAB 进行编程，得出列车运行速度V=80 km/h 前10 s 的荷载时程曲线及频谱图，如图1所示。

2 三维有限元模型的建立

为了研究供水管道在地铁振动和流体耦合作用下振动响应，采用ABAQUS 中的CFD 模块和Standard/Explicit 模块分别建立管道-管内水流流固耦合模型以及轨道-衬砌-土体-管道三维整体模型。

2.1 模型尺寸及网格划分

杨永斌［10］通过研究高速列车振动时振源至边界距离R不同时计算结果的收敛情况，指出当R为1.5倍最大剪切波长时，位移能达到较好的收敛结果；吕钟爱［11］指出当有限元网格的尺寸达到8～10 倍隧道直径时分析结果能有较好的精度；张宝才［12］则认为当模型深度大于7 倍隧道埋深，宽度大于15 倍隧道直径时，模型的自振周期才能趋于稳定。结合以上文献，为了保证模拟结果精度，本文根据最大剪切波长来确定模型尺寸，取180 m×120 m×90 m。研究表明，当单元尺寸长度L为λs/6时，λs为剪切波波长，可以使模拟结果获得较好的精度。本文模型中网格划分如图2所示。

图1 列车荷载时程曲线及频谱图Fig.1 Train load time history curve and spectrum diagram

图2 整体有限元模型Fig.2 Global finite element model

图3 管道有限元模型Fig.3 Finite element pipe model

图4 流体有限元模型Fig.4 Fluid finite element model

2.2 材料本构模型

管道采用高强度X65 管线钢，材料的本构模型采用徐震基于Ramberg-osgood 本构方程建立的更加符合实际的全局二段式应力-应变本构关系，该本构关系能更好地反映当ε＞ε0.2时X65 管线钢材料的本构关系［13］，应力-应变本构关系表达式如下：

式中：ε为总应变；εe为弹性应变；εp为塑性应变；σ为管材应力，单位MPa；E0为材料初始弹性模量，取2.07×105MPa。

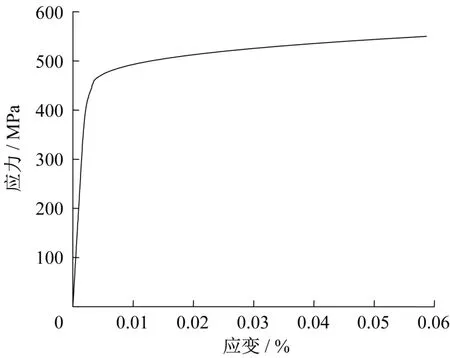
图5 X65管线钢的应力-应变关系Fig.5 Stress-strain relationship of X65 pipeline steel

轨道交通引起的土体动应变很小，一般处于弹性变形阶段。因此，土体模型采用弹性模型，本构关系可以用胡克定律表示，其式如下：

式中：｛σ｝为应力增量；｛ε｝为应变增量；［D］为弹性矩阵。

管道供水密度取1 000 kg/m3；材料模型选择EOS 中的 us-up，其中参数 C0 取 1 400；S取 0；Gamm0取0。

2.3 接触、荷载和边界条件施加

2.3.1 管土接触设置

ABAQUS 数值模拟中通常采用主控-从属接触面算法来模拟复杂的管土非线性相互作用。该接触算法中取管道外壁作为接触对主面，管道四周土体作为接触对从面且划分网格时，从属表面网格划分应比主控面更精细，以便计算收敛［14］。接触面相互作用分为法向接触和切向接触。将法向接触设置为硬接触，既只有当接触面在压紧状态时才能传递法向压力P，且压力P大小没有限制，接触面存在间隙时不传递法向压力P，压力和间隙关系如图6所示［15］。

切向设置为罚函数，即存在法向接触压力P时，接触面可以传递切向应力，摩擦力小于某一极限值τcrit时，接触面处于黏结状态，摩擦力大于τcrit时接触面发生相对滑动变形，处于滑移状态。τcrit的表达式如下：

式中：μ是摩擦系数，取 0.3；P为接触面的法向压力，单位为Pa。

隧道与周围土体单元采用绑定约束实现自由度耦合。

2.3.2 流固耦合作用和地铁振动荷载的施加

管道在受地铁振动作用时，管内流体作用对管道的应力场和位移场有很大影响，因此在分析供水管道在地铁作用下的振动响应时，有必要考虑流体和管道的相互作用，进行流固耦合分析。流固耦合分析中需要建立固体管道和流体两个模型，将管道与流体接触的耦合表面设置成Fluid-Structure Co-simulation相互作用，供水管道中存在压力，将入口和出口压力设置为0.6 MPa，同时考虑到管道中的水沿着管道方向匀速地流动，故将入口速度和出口速度设置为1.4 m/s，然后进行耦合求解，得到流固耦合作用下管道的结果文件，作为接下来分析步的预定义场，然后输入上述地铁振动荷载，进行管道振动响应计算。

2.3.3 边界条件施加

为了避免散射波在边界上产生反射造成结果误差，本模型土体四周采用刘晶波、杜修力提出的三维黏弹性人工边界［16］，其表达式如下：

切向：

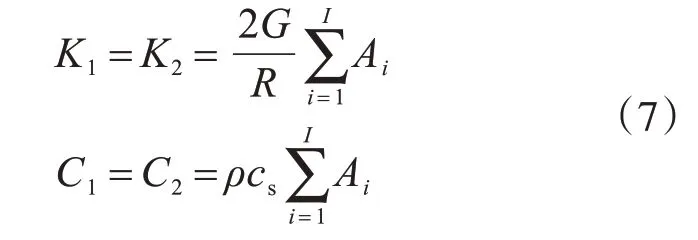
法向：

式中：G为介质的剪切模量；R为散射源到人工边界的距离；ρ为介质的密度；cs为介质的剪切波波速；cp为介质的压缩波波速；∑Ai为人工边界上节点所代表的面积。

土体下表面约束x、y、z三个方向的自由度，上表面不约束自由度为自由表面；衬砌和管道两端约束x、y、z轴三个方向的自由度。

3 计算结果与分析

依据上述网格划分和边界条件，模型参数取值如表2 所示。取阻尼比ξ=0.06，根据模态分析结果计算可得阻尼系数α=0.12，β=0.022；土层剪切波速取800 m/s。

表2 模型参数Table 2 Model parameters

在上述参数作用下，分别模拟管线在距隧道中心线不同距离、不同车速、不同埋深、不同管径等条件下的振动响应，进而得出不同因素对管道振动响应的影响规律。现有研究表明，在轨道交通振动中，竖向振动要远大于水平振动，故在本文中以竖向Y方向振动作为结果分析参数。列车速度为80 km/h时，隧道中心线处管道振动速度时程曲线及频谱如图7 所示，加速度时程曲线及频谱如图8所示。

图7 管道底部振动速度时程曲线及速度频谱图Fig.7 Time history curve and frequency spectrum of vibration velocity at the bottom of pipeline

图8 管道底部振动加速度时程曲线及加速度频谱图Fig.8 Time history curve and frequency spectrum of vibration acceleration at the bottom of pipeline

3.1 距隧道中心线不同距离

在车速分别为60 km/h、100 km/h、120 km/h车速下，供水管道底部的振动速度峰值、加速度峰值随距隧道中心线的距离增加变化趋势如图9、图10 所示。从图中可以看出，管道底部的速度峰值和加速度峰值随着距离隧道中心线距离的增大都呈现出衰减趋势，且在0 m 到60 m 范围内衰减幅度较大，60 m 之后衰减幅度较小，几乎没有变化。以车速100 km/h 为例，距隧道中心线0 m 到60 m的范围内，速度峰值从0.24 mm/s降低到0.04 mm/s，下降了约83.3%，加速度峰值从8.2 mm/s2降低到1.4 mm/s2，下降了约83%。由此可见，在对受地铁振动影响的供水管线监测中，要对隧道中心线60 m范围内的管线进行重点监测。

3.2 不同车速

图9 管道底部速度峰值随距离变化图Fig.9 Diagram of velocity peak at the bottom of the pipe changing with distance

图10 管道底部加速度峰值随距离变化图Fig.10 Diagram of peak acceleration at the bottom of the pipe changing with distance

在车速分别为 40 km/h、60 km/h、80 km/h、100 km/h、120 km/h 等五种固定车速条件下，分别提取距隧道中心线0 m、20 m、40 m、60 m、80 m 处管道底部的最大振动速度峰值（图11）和加速度峰值（图12）。从图中可以看出，管道距离隧道中心线相同位置处在不同车速下速度峰值和加速度峰值的变化趋势基本一致。管道振动的速度峰值和加速度峰值在车速从40 km/h 增加到100 km/h时增加幅度较大，以距隧道中心线0 m 处的振动响应规律为例，速度峰值从0.031 mm/s 增加到0.24 mm/s，加速度峰值从0.43 mm/s2增加到8.23 mm/s2；当速度从 100 km/h 增加到 120 km/h时，速度峰值和加速度峰值都出现了比较快的衰减，可见在速度增加的过程中存在一个卓越车速使管道的振动响应达到最大值，对管道运行安全极为不利。

3.3 不同埋深

图11 不同车速下速度峰值Fig.11 Peak speeds at different speeds

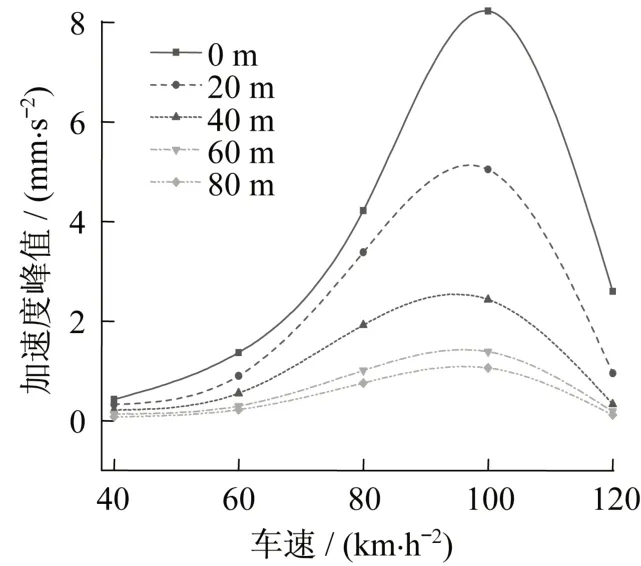
图12 不同车速下的加速度峰值Fig.12 Peak acceleration at different speeds

在车速为100 km/h 的车速下，分别模拟管道埋深为1 m、1.5 m、2 m、2.5 m、3 m 的最大速度峰值和加速度峰值如图13、图14所示。从图中可以看出，管道在不同埋深情况下速度峰值和加速度峰值曲线走势基本相似。随着埋深的减小距隧道距离中心线相同距离处速度峰值呈增加趋势，从0.24 mm/s 增加到了0.29 mm/s，增加了约20.8%，但在2 m 和2.5 m 处会出现反弹，可能是因为此处处于两土层交界处，上层岩体的密度和弹性模量都比下层岩体较大，波透过此边界时会发生折射和反射所致。随着埋深的减小加速度峰值呈增加趋势，加速度从7.25 mm/s2增加到8.23 mm/s2，增加了约14%。可见，埋深越小管道振动响应越大，对管道安全运行越不利。

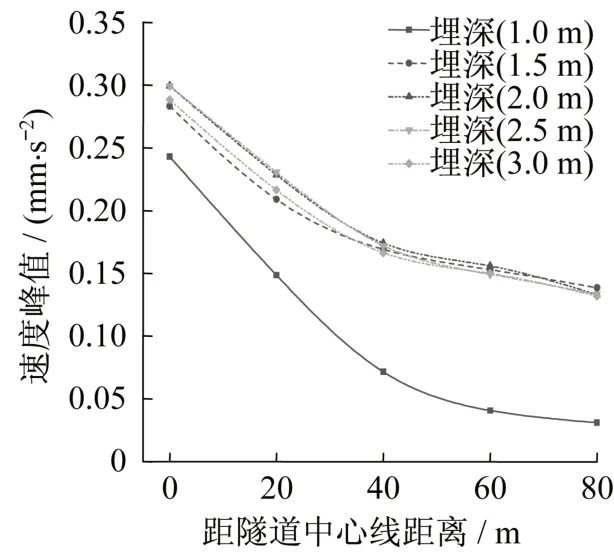
图13 不同埋深下速度峰值Fig.13 Peak velocity under different burial depths

图14 不同埋深下加速度峰值Fig.14 Peak acceleration at different burial depths

3.4 不同管径

在车速100 km/h、埋深1 m 的工况下，分别模拟管道直径为1 m、1.2 m、1.4 m、1.6 m、1.8 m 最大速度峰值和加速度峰值如图15、图16所示。从图中可以看出，随着管径的增大，管道的速度峰值和加速度峰值均呈现增加趋势。管道直径从1 m 增加到1.8 m 的过程中，管道速度峰值从0.21 mm/s增加到0.32 mm/s，增加了52.4%；管道加速度峰值从7.6 mm/s2增加到约18.6 mm/s2，增幅较大，大约增加了144.7%。可见，相同条件下，管道直径越大，振动响应越大，在设计受地铁振动影响的供水管道时，满足设计要求的情况下，应尽量采取较小直径。

图15 不同管径下速度峰值Fig.15 Peak velocity at different pipe diameters

4 结 论

图16 不同管径下加速度峰值Fig.16 Peak acceleration at different diameters

地铁运行时产生振动会通过轨道-衬砌-土体传至供水管道，从而引起管道振动响应，进而对供水管道造成影响破坏。使用ABAQUS 软件，分别建立流体-管内水流流固耦合模型和轨道-衬砌-土体-管道整体模型，分析供水管道在管内水流和地铁振动耦合作用下的振动响应，得出以下结论：从模拟结果上来看，在管内水流和地铁振动耦合作用下，速度峰值和加速度峰值都随着距隧道中心线的距离增加而减小；随着速度的增加而增加，且当车速达到一定速度后，随着速度的增加减小，表明存在一个卓越车速，在这个卓越车速下，管道的振动响应会出现极大值；随着埋深的增加而减小；随着管径的增大而增大。在实际工程中，应该根据实际工况来确定管线设计、埋深、管径等参数。