混凝土多孔砖墙单向振动倒塌试验研究
2020-08-27杨纪芒唐文豪
杨纪芒 李 翔 唐文豪
(同济大学建筑工程系,上海200092)
0 引 言
砌体结构历史悠久,应用广泛,是我国既有结构中数量最多的建筑。然而砌体材料强度低、延性差,结构容易在地震中出现倒塌现象。
近年来,考虑到环保和节能的需要,轻质、低产耗的混凝土多孔砖得到了广泛应用。由于新建房屋中仍会有造价低廉的砌体结构,而全国各地尚存大量砖木结构的历史保护建筑,所以有必要研究砌体结构房屋的抗震性能。震害调查发现,在地震作用下砖墙会发生剪切破坏(图1)[1],单层房屋及多层房屋顶层会发生弯曲破坏(图2)[2],而现有抗震规范[3]仅仅关注砖墙的剪切破坏,所以还需对单层房屋砖墙破坏机理进行试验研究。

图1 某民房墙体开裂[1]Fig.1 Wall of brick building crack

图2 纵墙倒出平面外[2]Fig.2 Out-of-plane behavior of wall
试验室常用的结构抗震试验方法包括拟静力试验、拟动力试验和振动台试验[4-5]。
拟静力试验是结构抗震研究常用的方法之一,其所需的设备简单,在试验过程中可以缓慢加载以便观测试件的开裂和破坏过程。课题组陈贡联对13 片混凝土多孔砖墙进行了低周反复荷载试验[6],提出了地震作用下混凝土多孔砖墙体受剪承载力及变形能力的计算方法。高之楠对6 片自保温混凝土多孔砖进行了平面内及平面外拟静力试验[7],给出了自保温混凝土多孔砖墙体平面内及平面外抗震承载力计算公式。但是,拟静力试验采用墙顶加载的方式不能模拟墙体由于自重所产生的惯性力,再加上其加载速率较低,不能完全真实地反映砖墙在地震中的抗震性能。
与拟静力试验不同,拟动力试验根据一个确定的地震反应来制定相应的加载方案。长沙理工大学课题组采用El-Centro 波[8],对8层24 m 1/2比例混凝土多孔砖砌体房屋子结构进行了拟动力试验。这种方法的关键是结构恢复力直接从试件上测得,无须对结构恢复力做任何理论上的假设,可以解决理论分析中恢复力模型及参数难以确定的困难。但是,拟动力试验不能真实反映应变速率对试件抗震性能的影响;其次,拟动力试验只能通过单个或多个加载器对试件加载,同样不能完全模拟地震作用时构件所受的惯性作用力。
模拟地震振动台试验可以再现各种地震波的作用过程,它是研究结构地震反应和破坏机理的最直接方法。课题组李翔等进行了5 个缩尺比为1/10的无筋砌体结构房屋模型的振动台试验[9-10],结果表明:在单向水平地震作用下,平面内受力的墙体会出现水平和斜向裂缝,但这不会直接引起模型的倒塌;砌体房屋的倒塌主要源于纵横墙协同工作能力的丧失,即地震作用方向垂直墙体平面外的失稳才是关键问题。试验虽初步揭示了砌体砖墙在振动作用下倒塌的机理,但试验结构为缩尺模型,存在重力失真效应,其研究结果仅具有参考价值。在已有的振动台试验中,限于振动台的承载能力,试件多数为缩尺结构模型[11-12]。而缩尺模型存在尺寸效应,且难以模拟实际结构的构造做法。除少数试验外[13-14],振动台试验往往在结构出现裂缝后就停止[15-16],这显然不利于全过程地了解砌体结构房屋倒塌机理。所以还需进行足尺结构全过程的抗震性能研究。
1 试验方案
1.1 试验装置及加载方案
在进行足尺结构试验前,课题组尝试设计制作了一个单向振动装置。如图3 所示,包括振动台、弹簧组、驱动装置、限位装置以及固定台座。振动台两侧通过弹簧组与固定台座相连,驱动装置为一300 kN 机械式千斤顶,每次试验前用它推动振动台至设定位置,迫使振动台产生初始位移。然后,由钢拉杆和螺母组成的限位装置将振动台固定在设定位置。试验时,释放限位装置,振动台将在弹簧组的驱动下作有阻尼的简谐振动(图4)。
系统弹簧刚度k为24 146 N/m,未装模型前振动台与弹簧的总质量m为39.3 kg,由式(1)可计算出装置机械振动的频率为3.84 Hz;实测该值为3.75 Hz,误差为2%。当初始位移为21 mm 时,由式(2)可计算得出振动台所能提供的最大加速度为12.24 m/s2,而实测最大加速度为11.86 m/s2,误差为3%,因此振动台能够提供有阻尼机械振动的试验条件。
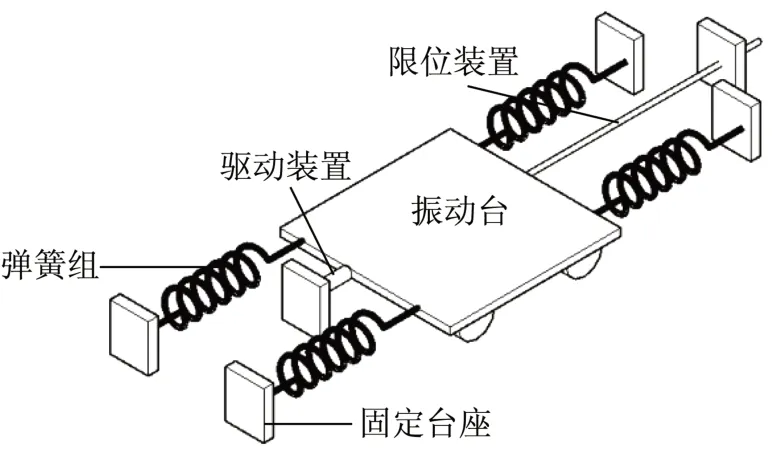
图3 振动台试验装置Fig.3 Setup for table test

图4 空振动台加速度时程曲线Fig.4 Acceleration record of shaking table without specimen

式中:T为振动周期,单位为 s;f为振动频率,单位为 Hz;m为试验装置总质量,单位为 kg;k为弹簧刚度,单位为N/mm;ω为圆频率,按式(3)计算;ξ为阻尼比,阻尼比小于0.1 时,对频率和周期的影响可忽略不计;ωd为有阻尼自由振动的角频率,按式(4)计算;a,α为计算系数,分别按式(5)计算。

式中:y0为振动初始位移,单位为mm;v0为振动初始速度,计算中取0。
将模型砌筑在振动台上,通过增大振动台的初始位移可以逐级增大振动台最大加速度的幅值,从而获取模型在不同机械波作用下的动力反应。
每次加载时,通过调整振动台初始位移,以20 mm 作为增量,逐级增加振动台的初始位移,提高每次振动加速度的峰值,直至模型破坏倒塌。
1.2 试件制作与测量系统
为摸清砌体砖墙在不同振动方向作用下的受力性能,试验设计了A,B 两个试件,两个试件均由一对半砖厚砖墙和一块木板组成,混凝土多孔砖尺寸为240 mm×115 mm×90 mm。每片砖墙采用5 块混凝土多孔砖和石膏砂浆砌筑而成,墙顶部放置一块10 mm 木板以模拟楼板,木板与砖块之间铺设石膏砂浆,木板上搁置2 块混凝土多孔砖,平面位置与下面砖墙对齐;砖墙底部用石膏砂浆固定在振动台槽钢中。试件由同一工人用同一批次的混凝土多孔砖和石膏砂浆砌筑而成。模型A 砖墙长边方向垂直于振动方向,试件B 砖墙长边方向平行于振动方向。
为摸清结构沿高度方向加速度的分布,在试件沿高度方向布置3 个采集频率为50 Hz 加速度传感器(图5),用以采集模型沿振动方向不同高度的加速度响应。在试件两片砖墙正前方各放置一个激光标线仪,用以在砖墙和振动台上投射出一条与振动方向垂直的竖直激光束。试验前,在有激光束一侧的墙体上沿不同高度黏贴3 条刻度条,以此来标定振动台的初始位移。同时在模型四周架设数码摄像机用于记录模型倒塌过程。

图5 模型及加速度传感器Fig.5 Models and accelerometers
1.3 材料力学性能试验
为了后续承载力分析,砌筑了4 个半砖墙厚试件测定试件沿通缝弯曲抗拉强度。每个试件采用9 块混凝土多孔砖和石膏砂浆砌筑而成,尺寸为240 mm×115 mm×1 080 mm。如图6 所示,采用工具式砌体抗弯强度试验加载装置,将大小两个钢架置于试件两侧,再用螺杆穿过试件中部预留的圆孔,连好两个钢架。通过手动旋转摇柄收紧螺杆,钢架上的加载点对试件施加弯矩,螺杆上产生的拉力通过连接在其一端的测力计测得。试验时,匀速转动摇柄加载,以每级0.1 kN作为增量加载,逐级读取并记录变形数据,直至试件破坏。4个试件破坏的位置都处于纯弯段,按式(6)计算混凝土多孔砖砌体沿通缝弯曲抗拉强度,计算精确到0.001 MPa,试验结果如表1所示,取4个试验数据的平均值0.118 MPa 作为混凝土多孔砖砌体沿通缝弯曲抗拉强度。

图6 弯曲抗拉试验装置Fig.6 Test setup for flexural tensile strength perpendicular to bed joint

表1 沿通缝弯曲抗拉强度试验结果Table 1 The test results of flexual tensile strength
同样地,采用3 个尺寸为240 mm×115 mm×270 mm 试件测定砌体沿通缝截面抗剪强度。如图7 所示,用重物堆载的方式进行抗剪强度试验。试验时,在中部的砖块上逐级堆放砝码,放上砝码后持续一分钟后未破坏再继续堆放砝码,直至试件破坏。混凝土多孔砖砌体沿通缝抗剪强度按式(7)计算,计算精确到0.001 MPa。如表2 所示,取3 个试验数据的平均值0.023 MPa 作为混凝土多孔砖砌体沿通缝截面抗剪强度。


式中:ft,i为沿通缝弯曲抗拉强度,单位为 MPa;fv,i为沿通缝抗剪强度,单位为MPa;N为试件受弯破坏荷载值,单位为N;P为试件抗剪破坏荷载值,单位为N;l为试件计算跨度,可取800 mm;b为试件截面宽度;h为试件截面高度,单位为mm。
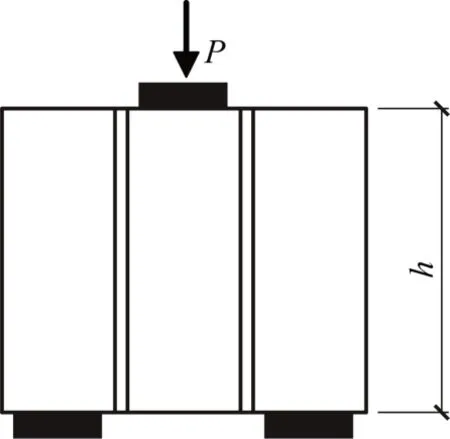
图7 抗剪试验装置Fig.7 Test setup for shearing strength perpendicular to bed joint

表2 沿通缝截面抗剪强度试验结果Table 2 The test results of shear strength
2 振动台试验结果
2.1 模型A试验
对砖木结构模型A沿垂直砖墙长边方向进行单向振动试验。振动台初始位移为20 mm 时,墙顶加速度峰值为4.17 m/s2,右侧砖墙位于木板上部的砖块与木板之间发生了滑移,滑移位移值为13 mm(图8)。当振动台初始位移为40 mm 时,墙顶加速度峰值为14.08 m/s2,砖墙底部第一层砖与第二层砖的灰缝受拉的一侧出现贯通的水平裂缝,第五层砖块与木板的灰缝受拉一侧同样出现贯通水平裂缝,最终两个界面粘结完全丧失,第二层到第五层砖块整体向左倒出平面外(图9)。
在振动台初始位移为20 mm时,砖墙顶部、中间和振动台底座三处加速度时程曲线如图10 所示,三个测点的加速度时程曲线几乎完全重合,可以认为在试件破坏之前,墙顶、墙中、振动台加速度的大小基本相同,即砖墙所受的惯性力可视作均布荷载。

图8 模型A墙顶开裂Fig.8 Model A cracked at top of the wall

图9 模型A倒塌Fig.9 Model A collapsed

图10 模型A加速度时程曲线Fig.10 Acceleration response of model A
2.2 模型B试验
对砖木结构模型B沿砖墙长边方向进行单向振动试验,振动台初始位移为20 mm时,墙顶加速度为6.50 m/s2,砖墙底部与振动台界面出现水平裂缝,但砖墙墙脚仍被固定在槽钢中。在振动台初始位移为40 mm时,试件绕墙脚边缘转动,底部明显抬升,离振动台最大竖向位移为10 mm;虽然墙脚与垫木起拱,但仍被槽钢约束在振动台上,墙顶加速度最大记录达到16.52 m/s2。当振动台初始位移为60 mm时,试件仍然绕墙脚边缘转动,此时试件底部抬离振动台最大竖向位移为38 mm,墙顶最大加速度为23.18 m/s2。在振动台的初始位移达到80 mm 时,砖墙第一层砖与第二层砖的界面左侧出现受弯裂缝(图11),试件底部抬离振动台最大竖向位移为46 mm,砖墙墙脚从台座的槽钢中拔出(图12),此时砖墙墙顶最大加速度为37.97 m/s2。

图11 模型B开裂转动Fig.11 Model B cracked and rotated

图12 模型B墙底拔出Fig.12 The bottom of model B was pulled out
在振动台初始位移为20 mm时,砖墙墙顶、中间和振动台底座三处的加速度时程曲线如图13所示,三个位置的加速度时程曲线几乎完全重合,可以认为在试件破坏之前,墙顶、墙中、振动台加速度的大小基本相同,即试件所受惯性力为均布荷载。

图13 模型B加速度时程曲线Fig.13 Acceleration response of model B
当振动台初始位移为20 mm 时,释放限位装置后,振动台达到最大加速度时,模型A,B 加速度沿高度分布如图14 所示,从图中可知,加速度沿高度方向近似可视为均匀分布。

图14 模型沿高度方向加速度分布Fig.14 Acceleration response of walls along their height
3 试验分析
3.1 墙底开裂承载力计算
如图14 所示,模型A,B 在振动台加速度达到最大时,砖墙加速度沿高度方向为均匀分布。考虑半砖墙自重所产生的惯性力(m=0.052 kg/mm)。由于底部砖块嵌固于台座槽钢中,而模型房屋为柔性方案,砖墙上部可视作为自由端,忽略轻质木板的影响,砖墙可简化为如图15 所示的计算模型。在惯性力的作用下,试件处于弯压剪复合受力状态,底部截面的受力最大,试件可能发生弯曲破坏也可能发生剪切破坏。底部截面的弯矩与剪力按式(8)和式(9)计算。

图15 砖墙受力计算简图Fig.15 Calculation diagram of model

式中,a为砖墙的加速度,单位为m/s2。
底部截面的抗弯承载能力Mr与抗剪承载力Vr按照式(10)和式(11)计算。


式中,W为砖墙抗弯截面模量;A为砖墙截面面积;b,h分别是砖墙水平截面的宽度和长度,单位为mm。
当式(10)等于式(8)时,可算得砖墙发生弯曲破坏所能承受的最大水平加速度值aM为

当式(11)等于式(9)时,可算得砖墙发生剪切破坏所能承受的最大水平加速度值av为

根据模型同批混凝土多孔砖材料抗弯强度ft和抗剪强度fv实测值,对模型A、B 砖墙高度都取450 mm;同时,模型A 砖墙水平截面长度h为115 mm,宽度b为240 mm,模型B 砖墙截面长度h为 240 mm,宽度b为 115 mm,代入式(12)和式(13)计算可得模型A发生弯曲破坏所能承受的最大水平加速度为11.76 m/s2,发生剪切破坏所能承受的最大水平加速度值为26.90 m/s2。模型B发生弯曲破坏所能承受的最大水平加速度为24.54 m/s2,发生剪切破坏所能承受的最大水平加速度值为26.90 m/s2。
由计算所得aM与av可知,模型A 和模型B 抗弯承载力均小于抗剪承载力,这与试验观察到的砖墙发生墙底弯曲受拉破坏现象相符。对于模型A,在振动台初始位移为40 mm 单向振动中,墙顶加速度最大达到14.08 m/s2,该值超过了试件抗弯承载力11.76 m/s2,结构发生弯曲破坏。对于模型B,在初始位移为80 mm 的单向振动中开裂,墙顶加速度最大值达到37.97 m/s2,该值超过了试件的抗弯承载力24.54 m/s2,试件底部弯曲受拉侧开裂。比较模型A,B 的承载力,可得平面内受力砖墙的抗震性能相对较好。
由受力砖墙墙底破坏时的抗弯、抗剪承载力计算式(12)、式(13)可知,当砖墙首先发生受弯破坏时:

简化后可得

根据模型同批混凝土多孔砖材料抗弯强度和抗剪强度实测值,将其代入式(15)可知:当平面外受力砖墙高厚比H/h大于1.71 时,砖墙会发生弯曲破坏。反之,砖墙破坏由抗剪承载力控制,即平面内受剪砖墙高宽比H/h小于1.71 时,砖墙会发生剪切破坏。由于模型A 平面外砖墙H/h=3.91,而模型B 平面内受力砖墙H/h=1.88,因此两个模型砖墙均发生弯曲破坏,与试验结果吻合良好。
3.2 砖墙倾覆时承载力计算
当砖墙顶部和底部全部开裂后,砖墙可视作刚体,在水平惯性力作用下将绕墙底边缘转动(图16)。由砖墙的倾覆力矩Mov计算式(16)和抗倾覆力矩MR计算式(17)可知,当刚体绕墙底边缘O转动时,砖墙倒塌。砖墙倾覆时所能承受的最大水平加速度值aov可按式(18)确定。

图16 砖墙受力计算简图Fig.16 Calculation diagram of model

式中:G为试件的总重,单位为N;g为重力加速度,可取 9.8 m/s2。
对模型A、B砖墙高度H都取450 mm。模型A墙厚h为115 mm,截面宽度b为240 mm。模型B水平截面高度h为240 mm,截面宽度b为115 mm。由式(18)计算可得:模型A 砖墙倾覆时所能承受的最大水平加速度值aov为2.50 m/s2,模型B 砖墙倾覆时所能承受的最大水平加速度值aov为5.23 m/s2。
比较模型A、B 发生弯曲破坏时所能承受的最大加速度aM与发生倾覆破坏时所能承受的最大加速度aov可知,模型倾覆时砖墙承载力远小于墙底受弯开裂时的承载力,这意味着一旦砖墙受弯破坏它将立即倾覆倒塌,这与模型A 发生弯曲破坏后立即倾覆的试验现象相符,但与模型B 试验现象不符。
考虑到模型B最终破坏形式为砖墙底部墙角从槽钢中拔出,所以式(18)不能直接用于计算模型B 倾覆时的承载力。如图17 所示,当开裂的砖墙墙脚从垫木中拔出时,由于两者相对运动产生摩擦力f,因此该竖向力对砖墙抗倾覆有利。以砌体与木材接触点O为转动中心,砖墙惯性力产生倾覆力矩Mov可按照式(19)计算,砖墙自重G,木块对砖墙的压力N和摩擦力f提供抗倾覆力矩MR可按照式(20)计算:

图17 砖墙受力计算简图Fig.17 Calculation diagram of model

式中,c为砖墙与木块接触点O到砖墙底部的距离,取50 mm。
按照《砌体结构设计规范》[17]中第 3.2.5 条规定,砌体沿木材滑动且两者界面干燥时的摩擦系数μ可取0.6,根据第7.4.4 条规定,砌体与木材接触点压力R取2maH,可得N为maH。当倾覆力矩大于抗倾覆力矩时,砖墙会发生倾覆,发生倾覆需要的最小加速度按式(21)计算。

对于试件B,砖墙高度H取540 mm,截面高度h取240 mm,计算可得发生倾覆时最小加速度为45.23 m/s2,该值大于B 试件最后一个工况的最大加速度37.97 m/s2,所以试件不会发生倾覆,这与试验现象墙脚沿槽钢上下滑移并被拔出但试件并未倒塌吻合。
4 结 论
在单向机械波作用下,砌体结构模型与振动台一起作有阻尼自由振动,砖墙加速度反应沿高度方向均匀分布。随着振动台初始位移逐级增加,结构最大加速度峰值逐渐加大。楼板和墙顶界面是结构的薄弱位置,墙顶开裂后,墙底也会出现水平裂缝。一旦墙底开裂,垂直于振动方向、平面外受力的砖墙极易倾覆倒出平面外;沿着振动方向、平面内受力的砖墙则会绕着墙脚晃动。砖墙受弯开裂后平面外倾覆是结构倒塌的主要原因。分析表明:砖墙的破坏形式与砖墙材料沿通缝弯曲抗拉强度与沿通缝抗剪强度的比值、砖墙的高厚比有关。在本次小型振动台倒塌试验的基础上,课题组将制作大型振动台进行足尺砌体结构试验以揭示砌体结构房屋倒塌机理。
