基于LDA-GA-SVM的船舶电力推进系统故障诊断

赖永发,徐合力,高 岚

(武汉理工大学 船舶动力工程技术交通行业重点实验室，湖北 武汉 430063)

船舶电力推进系统发生故障时，快速准确地诊断出故障原因，不仅可以降低经济损失，还可以极大地降低维修成本。

国内外许多学者对信号处理与人工智能结合的船舶电力推进系统故障诊断方法做了大量研究。Andre A Silva[1]等利用小波变换过滤传感器数据最佳信息丰富区域，增强电力驱动船的诊断准确性以及简化计算。对于螺旋桨的桨叶断裂、缠绕和撞击异物故障诊断，可利用小波分析的信号奇异性检测方法对推进电机定子电流信号进行分析[2]。还有学者提出利用粒子群算法和灰色关联分析法分别对BP神经网络的权值与阈值进行寻优以提高诊断准确率[3-4]。朱凤波[5]等利用线性判别分析(LDA)分别与隐马尔科夫模型和BP神经网络结合实现了模拟电路早期故障诊断，BP神经网络是应用较为广泛的神经网络，是以逆向传播算法作为核心思想的多层前馈神经网络。

神经网络在小样本情况下，易出现过拟合情况。以统计学理论为基础的支持向量机(SVM)算法能有效解决小样本分类的问题[6-7]。钟崴[8]等利用小波包提取管屏振动信号的特征能量，作为支持向量机的输入进行故障分类。朱艳伟[9]等采用小波包结合支持向量机对孤岛与扰动情况进行鉴别。

1 特征提取与降维原理

1.1 小波包变换

小波包变换是在小波变换的基础上推广而来的，弥补了小波变换高频段频率分辨率差的缺点。小波包分解的实质是产生一组高、低通滤波器对故障信号进行分解[10]。

小波包分解以及重构公式为：

(1)

fj,n(tn)=

(2)

小波包分解后每个频段的频谱能量公式为：

(3)

式中，Ej,n为信号经小波包分解后的第j层第n个节点的频带能量；fj,n(k)为节点(j,n)重构后第k个采样点幅值；m为重构后采样点数。

根据各频带小波包能量，构造l维特征向量[λ1，λ2,…,λl]，其中：

(4)

式中，λn为l维特征向量中的第n个特征值；Emin、Emax分别为第j层分解频带中的最小和最大频带能量。

由小波包能量分析理论可知，电流和转矩信号进行小波包变换得到的特征向量特征，能反映船舶电力推进系统的故障状态。

1.2 线性判别分析(LDA)

LDA是一种有监督的线性降维算法，其核心思想是得到一个最佳投影方向，使得原始样本经过该投影后类内方差最小，类间方差最大，从而实现样本降维[5]。

利用LDA进行特征向量降维的算法流程如下：

1)计算类内散度矩阵Se：

(5)

式中，Xj为第j类样本特征集合；x为样本数据；μj为第j类样本均值向量。

2)计算类间散度矩阵Sf：

(6)

式中，Nj为第j类样本数；μ为所有样本的均值向量。

(7)

4)计算在投影矩阵下的降维特征集：

xi=WTui,

(8)

式中，xi为投影矩阵下新生成的降维特征样本，其维数为d;ui为原样本特征。

2 基于GA-SVM的故障识别算法

2.1 支持向量机(SVM)

SVM旨在求解高维空间中的最优分类超平面，使得样本线性可分[8]。图1为SVM最优分类超平面示意图。由图1看出，有2类线性可分数据样本点分别位于H面的两侧，H为分类超平面，这样的分类超平面有无数个；H1、H2为穿过最接近分类面的样本点且平行于H的面，即正、负支持向量，SVM的核心思想就是找到唯一分类超平面H，使得H1、H2间的分类间隔(margin)2/‖w‖最大化。

图1 SVM最优分类超平面示意图

分类超平面可表示为：

w·x+b=0，

(9)

式中，w为权值矢量;b为偏置系数。

To为线性样本集，To={(x1,y1),…,(xn,yn)},xi∈R,yi∈{-1,1}，则根据支持向量机的核心思想，可将求解最优分类面问题转化为以下最优化问题：

(10)

式中，s.t.为约束条件;yi为类别标签;C为惩罚参数;ξi为松弛变量。

式(11)为凸二次规划问题，将其转化为对偶问题：

(11)

f(x)=sgn[(w*·x)+b*]

(12)

SVM模型的故障诊断准确率ηp表达式为：

(13)

式中，N为测试样本总数;Np为测试样本中分类正确数。

2.2 遗传算法(GA)对SVM参数寻优

惩罚因子C与核函数参数γ对SVM的诊断准确率的影响极大，本文利用遗传算法对SVM参数C和γ进行寻优[11]。GA优化SVM参数流程图如图2所示。首先，用二进制对参数C和γ进行个体编码产生初始种群；然后，计算个体的适应度值，以交叉验证(CV)下的准确率作为适应度值；接着进行选择、变异、交叉操作得到新的种群；上述进化过程迭代至满足条件方可停止；最后对得到的最优参数解码并代入SVM中训练得到最佳诊断模型。

图2 GA优化SVM参数流程图

3 船舶电力推进系统故障仿真模型

以中铁渤海铁路轮渡“烟大轮”作为母型船，用ANSYS-Simplorer、ANSYS-Maxwell和Simulink软件搭建船舶电力推进系统联合仿真模型，所采用的控制策略为SVPWM，给定转速指令为150 r/min。其永磁同步推进电机参数及船桨参数如表1、表2所示[12]。

表1 永磁同步推进电机参数

表2 “烟大轮”母型船船桨参数

根据文献[13]的方法，在ANSYS-Maxwell上通过改变短路匝数、定子电阻和漏抗值，建立不同程度的匝间短路故障模型。而单相接地和相间短路故障在Simplorer中的逆变器电路中设置。最终得到9类故障仿真模型。

图3～图6分别为电力推进系统正常状态和9种故障状态中3种的三相电流与转矩波形。电流波形中，实线为A相，虚线为B相，点划线为C相。

图3 正常电流与转矩波形

图4 A相匝间短路(2匝)电流与转矩仿真波形

系统发生故障时，三相电流的平衡状态被打破，每相电流的相位均发生变化。尤其是发生单相接地和相间短路时，电流信号完全畸变，转矩波动也随之变大，电流的波动幅度增加至正常时的2倍以上。正常状态下的转矩在80～90 kN·m之间波动，发生故障时，波动幅度大幅增加到115 kN·m。

图5 AB相间短路电流与转矩仿真波形

图6 A相接地电流与转矩波形

4 数值试验与结果分析

图7所示为船舶电力推进系统故障诊断设计流程图，其流程主要分为如下3个步骤。

1)故障特征提取。计算原始故障数据经小波包重构后的能量值，构造特征向量，再利用LDA对特征样本进行降维处理。

2)GA-SVM模型训练。使用GA算法对SVM参数寻优，利用训练样本训练优化后的模型。

3)GA-SVM模型测试。用测试样本对训练后的SVM模型进行测试，计算诊断准确率。

图7 电力推进系统故障诊断系统设计流程图

采集三相电流与转矩信号，采样频率为1 024 Hz，数据长度为1 024个采样点。每种故障状态各采集100组数据，对故障信号进行5层小波包分解和重构，小波包基为db4，得到32个频段的重构信号，每个频段的带宽为16 Hz。按式(3)和式(4)计算得到32个能量特征值。

图8为正常状态下频带能量分布，图9为A相匝间短路(2匝)频带能量分布。由图8知，当船舶电力推进系统运行在正常状态下，电流信号中几乎只存在基波频率(存在于第2个节点频带)，其他谐波成分的能量幅值很小，同样，转矩信号的幅值除了第1个频带外，其他频带幅值几乎为0。由图9知，A相匝间短路(2匝)的电流与转矩频带能量和正常状态对比，基波以及其他谐波所在频带的能量均发生了很大变化。因此，可将每相电流和转矩的频带能量作为特征值，最后构造一个1 000×128的特征样本矩阵。

图8 正常状态下频带能量分布

图9 A相匝间短路(2匝)频带能量分布

表3为故障分类标签表，表4为各故障状态降维后的新特征向量。

表3 故障分类标签表

特征样本矩阵维数为128维，若直接将其作为SVM的输入，容易导致维数灾难现象。利用LDA算法对带标签的样本矩阵进行降维处理，得到9维样本矩阵。从每种新的故障特征样本中随机选取70组作为训练样本，共得到700组训练样本。剩下的30组特征样本作为测试样本，共得到300组测试样本。

表4 各故障样本降维后的新特征向量

船舶电力推进系统故障诊断属于多分类识别方法，故本文采用一对一方法设计多分类器。采用径向基函数(RBF)作为核函数。首先根据经验确定SVM的惩罚参数C=2和核函数参数γ=1，用训练样本作为输入训练SVM模型，再用训练好的模型对测试样本进行故障分类，结果如图10所示，准确率只有94.67%，正确分类的样本数为284组。其中，故障类别2、5、7、8、9均能准确分类，误判最为严重的是故障类别3和4。

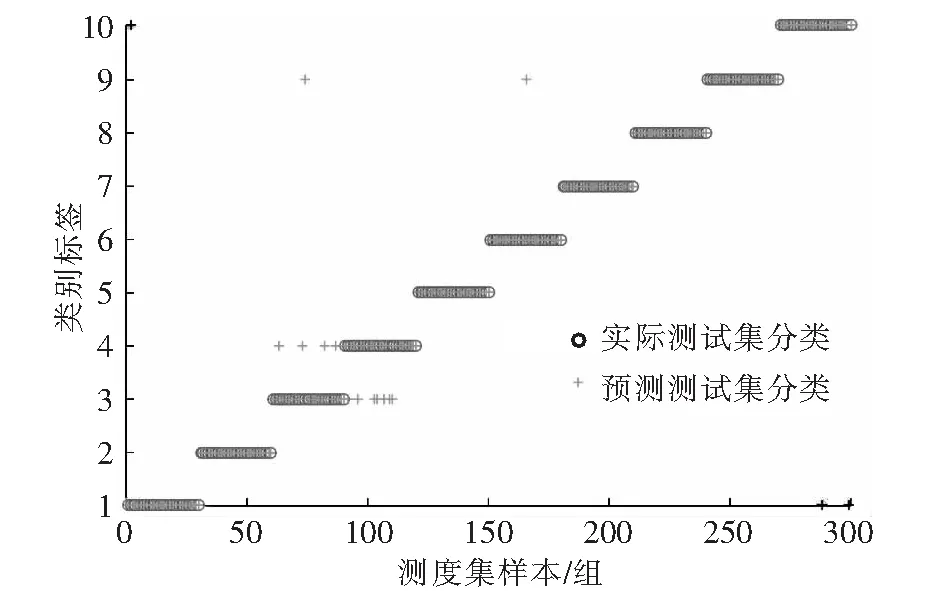
图10 未优化的SVM分类结果图

利用遗传算法对参数C和γ进行寻优，其中遗传算法的参数设置为：初始种群数量为20，进化代数为60，代沟为0.9，交叉概率为0.7，变异概率为0.01，参数C和γ的范围均为[0，100]。以5折交叉验证方法下的准确率作为SVM训练时的适应度值。

训练后的GA-SVM模型经测试样本验证得到的GA迭代结果和分类结果见图11。从图11知，种群最优个体的适应度值最后稳定在97.67%，最佳参数为：C=2.298 5、γ=98.102 4。经GA算法优化的SVM模型对测试样本的分类结果如图12所示，分类准确率达97.67%，正确分类样本数为293组。在未优化的SVM模型中，被误判的故障类别1、6、10均能在GA-SVM模型中准确分类，故障类别3、4的误判率也有所降低，通过基于GA-SVM模型的分类准确率提高了2%。

图11 基于GA优化SVM的迭代运算图

图12 基于GA优化SVM的分类结果图

为验证LDA降维后的GA-SVM诊断模型的适用性，将原始128维特征矩阵直接作为未优化SVM(C=2、γ=1)和GA-SVM(C=2.284 6、γ=0.040 8)的输入，得到对128维测试样本分类结果。测试集样本数量为300组，不同故障诊断模型的分类结果对比如表5所示，可以发现经过GA优化的SVM故障分类准确率均比未优化的SVM的高，同时经LDA降维后的特征矩阵作为诊断模型的输入亦提高了分类准确率。

表5 不同故障诊断模型的分类结果对比

5 结束语

1)本文以“烟大轮”作为研究对象，搭建其电力推进系统联合仿真模型，并且采集到电力推进系统正常与故障状态下的数据。利用LDA算法对小波包变换后得到的特征矩阵进行降维，将其作为SVM的输入。分类结果表明，LDA能有效剔除故障样本中的冗余信息，提高SVM的效率和准确率。

2)提出利用GA算法对SVM的参数进行寻优，解决了依靠经验试凑确定SVM参数的麻烦。实验结果表明，无论是否对特征矩阵进行了降维操作，经GA算法优化参数后的SVM模型都提高了船舶电力推进系统的故障分类准确率。