基于GA-BP的船舶同步发电机定转子绕组匝间短路故障诊断研究

孙卫鹏，徐合力，高 岚

(武汉理工大学 能源与动力工程学院，湖北 武汉 430063)

船舶同步发电机是船舶电力系统的重要组成部分，由于其恶劣的工作环境以及制造过程中产生的缺陷加上人员操作不规范，发电机容易产生电气以及机械故障[1]。其中，发电机定子绕组匝间短路故障以及转子励磁绕组匝间短路故障是发电机内部较常见的电气故障，易对船舶及工作人员造成安全威胁。因此对发电机故障进行诊断研究，从而对故障进行快速处理具有重要的意义。

随着人工智能技术的发展，故障诊断方法逐步从传统故障诊断转变为人工智能故障诊断。与此对应的即是模式识别方法的改变，通过提取诊断对象数据的特征参数，利用人工神经网络进行分类识别，进而达到故障诊断的目的[2-4]。其中，BP神经网络是广泛使用的一种神经网络，它具有可靠性高、实用性好、运算速度快的优点，但也有易陷入局部极小值、学习效率低、收敛速度慢的缺点[5-6]。本文利用遗传算法(GA)对BP神经网络进行优化(GA-BP神经网络)，以提高其诊断性能。

输入样本的维数对BP神经网络的建立、学习以及诊断效率有较大的影响，当输入样本的维数较高时，需要降低输入样本的维数。其中，主成分分析法(PCA)是一种常用的数据降维方法，目前广泛应用于故障诊断领域[7]。本文以某小型船舶同步发电机参数为例，在Maxwell软件平台上进行故障仿真，利用小波包以及PCA对仿真数据进行故障特征提取，生成样本数据，对GA-BP神经网络进行训练测试，从而实现对船舶同步发电机的故障诊断。

1 同步发电机故障分析

1.1 同步发电机模型

本文以一台小型船用同步发电机为例，探究了在额定工况下不同程度的定子以及转子绕组匝间短路对发电机性能的影响。利用ANSYS Maxwell软件中的RMxprt模块，选择三相凸极电机模型，输入同步发电机的结构参数，生成RMxprt模型，再通过对RMxprt模型求解生成Maxwell2D模型，并完成模型的材料分配、网格剖分以及边界条件设置。为更好的观察同步发电机定子以及转子绕组匝间短路故障对发电机性能的影响，本文通过外电路设置发电机激励源，通过短路发电机定子以及转子绕组的线圈来模拟匝间短路故障。表1为同步发电机的主要参数。

表1 同步发电机主要参数表

1.2 同步发电机故障仿真

针对同步发电机定子绕组匝间短路故障，对A相绕组进行5.0%、12.5%、30.0%、45.0%4种不同程度的故障状况模拟；针对同步发电机转子励磁绕组匝间短路故障，对其进行12.5%、25.0%、50.0% 3种不同程度的故障状况模拟。数据采样频率为1 250 Hz，仿真步长为0.000 8 s，采样周期为0.4 s，利用三相电流信号对发电机故障进行诊断，选取从0.56 s到0.60 s，总共为0.04 s的发电机数据波形进行分析。图1为发电机在正常以及故障状态下的三相电流仿真波形。图1中,实线为A相电流仿真波形,虚线为B相电流仿真波形,点划线为C相电流仿真波形。

由图1可知，正常状态下发电机的三相电流具有对称性。当发生定子绕组匝间短路时，发电机三相电流对称性被打破，电流幅值均减小，其中A相电流幅值随着故障程度的加深而减小，B、C相电流幅值基本维持不变。当发生转子励磁绕组匝间短路故障时，发电机三相电流对称性同样被打破，A、B、C相电流幅值随着故障程度的加深而减小，且不对称程度逐渐增加。针对以上仿真结果，对仿真数据作进一步的处理。

2 基于小波包和PCA的特征提取

在故障诊断过程中，从数据中提取特征向量是关键的一步。本文利用小波包对三相电流信号进行分解重构，得到在不同频带下的信号波形，并将各频带信号的能量占比作为特征向量输出。再利用PCA方法对高维特征向量进行降维，以避免高维数的输入向量对神经网络诊断结果的影响。

2.1 基于小波包的特征向量生成

由于发电机发生匝间短路故障时三相电流信号存在不对称性以及各类谐波，因此需要对三相电流的频率信息进行细致的划分。利用4层小波包对正常以及短路故障下的每一个采样周期的电流信号进行分解，生成16个频带[S(4,i),i=0,1,2，…，15]的重构信号,其中小波函数选择db5。图2为定子绕组5.0%匝间短路故障下的一个采样周期(0.4 s)内的小波包重构信号图，仅选用A相电流信号作为处理对象来进行展示。

根据上述16个频带的重构信号，将每个频带的能量占比作为电流信号的多维特征向量输出，具体步骤如下。

图1 发电机正常以及故障状态下三相电流仿真波形

1)求取各个频带的能量值E4i(i=0,1,…,15)：

(1)

式中，xik(i=0,1,2，…，15；k=1,2,…,n)为重构信号S4i离散点的幅值。

2)计算重构后16个频带的总能量E，用ei来表示每个频带的能量占比：

(2)

(3)

3)构造电流信号的特征向量Xi(已进行归一化处理)：

Xi=[e0,e1,e2，…，e15]T,

(4)

同步发电机在正常状态以及匝间短路故障状态下，由于其A相电流重构信号16个频带的能量占比数据主要集中在前半部分，因此仅对前10个频带的能量占比进行展示，如表2所示。由表2可知，正常状态、5.0%、12.5%、30.0%定子绕组匝间短路，12.5%、25.0%、50.0%转子励磁绕组匝间短路的能量主要集中在1、2、3、4、5频带，45.0%定子绕组匝间短路的能量主要集中在1、2、4、5、7频带。

图2 定子绕组5.0%匝间短路故障下A相电流4层小波包重构信号波形图

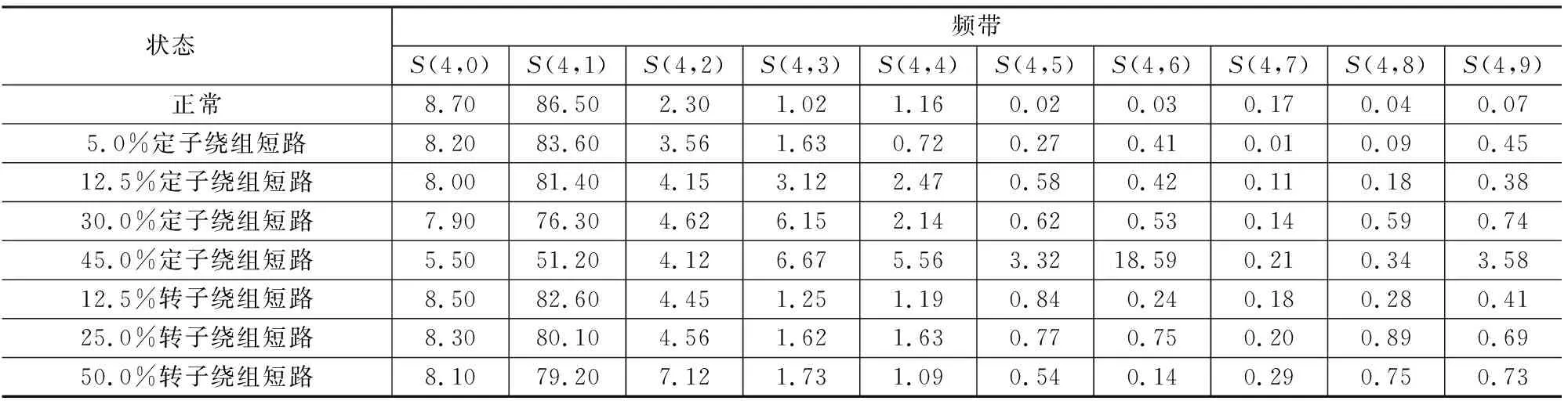
表2 不同状态下A相电流重构信号频带能量占比表

2.2 PCA降维

一相电流信号经4层小波包分解重构后生成16维特征向量，三相电流信号将总共生成48维特征向量。由于特征向量维数较大，易对BP神经网络的训练诊断产生影响，因此利用PCA对小波包分解重构后的每相电流的特征向量进行降维，从16维特征向量中提取最有价值的特征向量汇总组合成神经网络的输入样本，以此达到改善神经网络诊断能力的目的。16维特征向量所对应的特征值的贡献率如表3所示，表中按照从大到小排列，排名越靠后贡献率越小，因此仅展示前10特征值的贡献率情况。

表3 16维特征向量所对应的前10特征值的贡献率 %

由表3可知，利用PCA对发电机不同状态下的16维特征向量进行降维后，除45.0%定子绕组匝间短路故障状态下前5个主元累计贡献率方能达到95%外，其他状态下前3个主元累计贡献率即可达到95%。为了不使有效数据丢失，选择将16维特征向量降为5维，因此BP神经网络输入层的个数确定为15。

3 GA-BP神经网络

GA是通过模拟自然界“优胜劣汰”法则，根据选择和遗传的机理来寻求最优解的一种搜索寻优方法，具有良好的全局寻优能力[8-9]。本文通过利用GA-BP神经网络的权值和阈值来弥补BP神经网络收敛速度慢以及易陷入局部极优值的缺陷。GA-BP神经网络的运算过程如下。

1)建立BP神经网络结构，设置输入层、输出层和隐含层节点个数，初始化权值和阈值。

2)对BP神经网络初始权值阈值选用实数进行编码。

3)利用训练样本对BP神经网络进行学习训练，利用适应度函数计算种群中每个个体的适应度值，适应度函数f的表达式为：

(5)

式中，aij为神经网络训练后的实际输出值;tij为对应的期望输出值；N为训练样本总数；q为神经网络输出神经元数量。

4)对种群个体进行选择交叉变异操作。从种群中选择若干个体用于繁殖后代，每个个体被选取的概率Pk为：

(6)

式中，c为种群中的个体数目；fk为个体k的适应度值。

从选取的个体中随机抽取2个个体进行配对，以交叉概率Pc交换两者部分基因形成2个新的个体。则第l1和l2个个体在第o位的基因交叉操作如下：

(7)

式中，gl1,o和gl2,o分别为第l1和l2个个体在第o位的基因；r为[0,1]之间的随机数。

以一个较小的变异概率Pv选择第k个个体的第o位基因进行变异操作生成新的个体来增加种群的多样性，其操作方法如下：

(8)

式中，gmax和gmin分别为基因gko的上限和下限；r1为随机数；s为当前的迭代次数；smax为最大进化代数；r2为[0,1]之间的随机数。

5)计算每代的最小适应度值。当最小适应度值不再变化或者达到最大迭代次数则停止计算并进行下一步操作，否则返回步骤3)继续进行计算。

6)将得到的最优个体进行解码并计算出相应的最优权值阈值，并应用到BP神经网络中。

7)利用训练样本对应用最优权值阈值后的BP神经网络进行学习训练，计算训练结果输出误差。

8)利用BP神经网路训练结果的输出误差对网络的权值阈值进行更新，当达到预定的训练精度或者训练次数时结束训练，否则返回步骤7)继续进行计算。

4 故障实验分析

采集同步发电机在3种状态(正常、定子绕组匝间短路、转子励磁绕组匝间短路)下的三相电流信号，按照上述方法进行特征提取，构成800组15维的样本数据，其中正常状态以及不同程度的故障状态各100组。从800组样本数据中随机抽取700组作为训练样本，剩下的100组样本作为测试样本。

将发电机正常工况、5.0%定子绕组匝间短路、12.5%定子绕组匝间短路、30.0%定子绕组匝间短路、45.0%定子绕组匝间短路、12.5%转子励磁绕组匝间短路、25.0%转子励磁绕组匝间短路、50.0%转子励磁绕组匝间短路作为神经网络的输出，并对其进行二进制编码，状态编码表见表4。

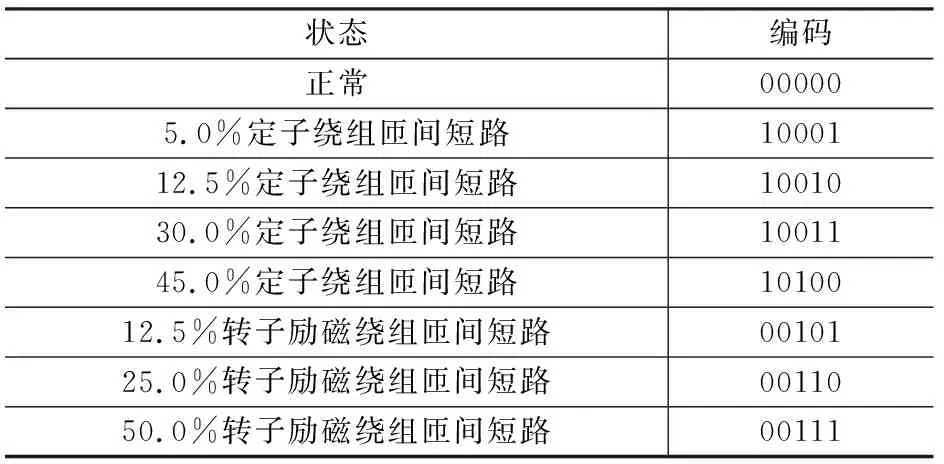
表4 状态编码表

根据以上分析，本文采用的BP神经网络故障诊断模型具有15个输入特征量和5个输出特征量，因此该神经网络的输入层、输出层的神经元数分别是H=15、M=5，设置网络的最大训练次数为1 000，梯度下降法的学习率为0.01；并设置收敛精度为0.001。设置遗传算法种群数目为20，进化次数为30，交叉概率为0.2，变异概率为0.1。

隐含层节神经元数I需要根据以下经验公式进一步确定：

(9)

式中，H、M分别为神经网络输入层、输出层神经元个数，b为0～10的常数。

由公式(9)知，隐含层节点数在4～14之间，从中选取效果最佳的隐含层节点数。利用训练样本对不同隐含层节点的神经网络进行训练，图3为不同隐含层节点数下的BP神经网络训练精度。

图3 不同隐含层节点数下的BP神经网络训练精度

由图3可知，当隐含层节点数为10时神经网络训练精度最小，因此确定隐含层节点数为10。图4为传统BP神经网络以及GA-BP神经网络训练误差变化曲线。可看出，GA-BP神经网络收敛效率优于传统BP神经网络，克服了传统BP神经网络后期陷入局部极小值，影响收敛速度的缺点。

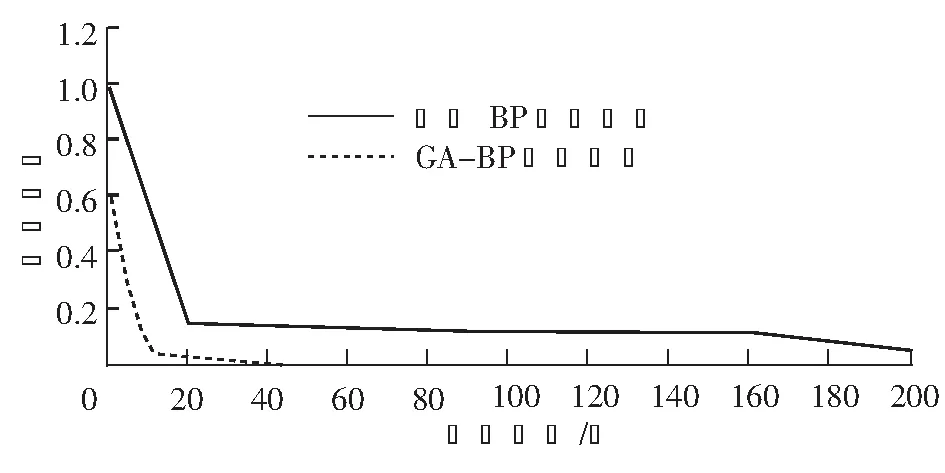
图4 2种神经网络训练误差变化曲线

2种神经网络训练完毕后，利用100组测试样本分别对2种神经网络诊断效果进行测试，表5列出了2种神经网络测试的部分输出向量。由表5中测试结果计算可得：BP神经网络诊断准确率为98.56%,GA-BP神经网络的诊断准确率则为99.67%，GA-BP神经网络的诊断精度最高，也反映了基于PCA和GA-BP神经网络的诊断方法具有较好的效果。

5 结束语

本文针对船舶同步发电机定转子绕组匝间短路问题，利用Maxwell软件进行发电机正常状态以及匝间短路故障状态仿真，采集三相电流信号对故障状况进行分析，发现当发生匝间短路故障时，三相电流对称性被打破，且电流幅值随着故障程度加深而减小。利用小波包分解重构以及PCA降维提取故障特征向量，分别对传统BP神经网络以及GA-BP神经网络进行训练测试。结果表明，GA-BP神经网络在发电机匝间短路故障诊断中具备更好的快速性和准确性，满足故障诊断的要求，在实际工程中有一定的应用价值。

表5 测试结果对比表