基于蒙特卡洛模拟的井眼轨迹测斜计算方法对比分析研究
2020-08-27陈庚绪李红星王新刚白雪龙王越支
陈庚绪,樊 锐,李红星,王新刚,白雪龙,王越支
(1长江大学石油工程学院 2中国石油集团渤海钻探工程有限公司第二钻井工程分公司 3中海油服油技塘沽作业公司)
井眼轨迹测斜计算方法很多,常见的有平均角法、校正平均角法、平衡正切法、最小曲率法、曲率半径法和弦步法等,不论哪种方法都是将测点之间的测段假定为某种特定的线段,但是测段间真实客观存在的井眼轨迹形状是无法预知的,故测斜计算得到的井眼轨迹与真实客观存在的井眼轨迹必然不相同。针对井眼轨迹测斜计算误差问题,陈炜卿、管志川等学者通过构造理论参考曲线,对不同测斜计算方法计算的平均井眼位置进行了大样本空间对比分析,得出所有测斜计算方法表现出来的误差特性都很相似的结论,并用统一的解析式表示了所有的测斜计算方法所产生的误差概率密度函数,但是误差和不确定度是两个不同的概念,他们没有从不确定度的角度去进一步分析[1-2]。
最小曲率法是建立在如下假设基础上的:①最小曲率法是基于分段近似,假设测点之间的曲率为定值;②最小曲率法是一阶连续的,但它在二阶导数和三阶导数中表现出不连续性。对于给定的一组测点,实际井眼轨迹可能是曲线段和直线段的混合曲线,而不是连续的曲线,就算是先进的旋转导向工具(RSS)也不能钻出连续曲线。在众多井眼轨迹计算方法中,样条曲线法基于线性代数方法,对于一阶,二阶和三阶都是连续的。样条曲线法能有效使得给定测段的曲率和曲率变化率连续(二阶和三阶)[3-6]。
图1显示了用最小曲率法计算两测点之间的三种可能的井眼轨迹,由与测斜数据相匹配的圆弧表示。中间的圆弧为最小曲率法计算的井眼轨迹,因测点间可能是复合钻进和滑动钻进交叉进行且两者之比无法确定,故另外两条井眼轨迹不同于用最小曲率法计算的井眼轨迹,从而导致井眼曲率(二阶)不连续。这种不连续性导致由每个圆弧的半径表示的恒定曲率半径产生了差异。最小曲率法与样条曲线法的区别是一个只能保证函数值连续,另一个除了保证函数值连续还保证它的导数也连续。
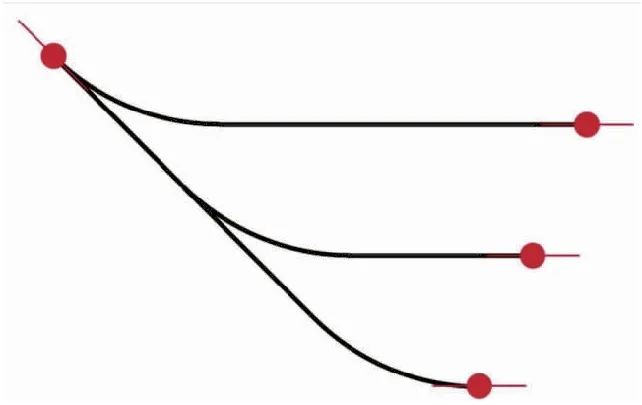
图1 两测点间滑动距离不同对测段的影响
一、井眼轨迹计算方法的蒙特卡洛模拟
蒙特卡洛模拟是基于概率统计的一种算法[7],若需模拟井眼轨迹误差不确定度,需要先建立概率统计模型,其次确定模型中误差变量数据的分布,然后根据误差变量的精度要求确定模拟抽样次数,最后在随机抽样产生结果的基础上实现概率统计分析,随机抽样的次数越多,井眼轨迹位置越逼近真实值。在本研究中,井眼轨迹测斜计算方法即概率统计计算模型,模型中的误差变量为井斜角误差、方位角误差和井深误差。本研究主要围绕最小曲率法、曲率半径法和样条曲线法展开蒙特卡洛模拟分析。
1.井眼轨迹测斜计算模型
最小曲率法和曲率半径法是常见的井眼轨迹测斜计算方法,这两种计算方法不再累述。样条曲线法假设井眼轨迹是一个由三次多项式组成的函数,且函数一阶导、二阶导在所有测点都是连续的,其测斜计算模型为[7]:
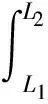
(1)
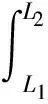
(2)
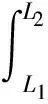
(3)
式(1)~式(3)中:ΔV、ΔN和ΔE—分别为垂深、北坐标和东坐标增量,m;I和A—井斜角和方位角,°;ΔI和ΔA—井斜角和方位角增量,°;ΔL—测段长,m。
2.井眼轨迹误差变量分布及精度的确定
1999年威廉姆森对于各种测量工具和测量类型,在特定井眼条件下给定误差的加权函数,测量误差得到了很好的理解和建模。加权函数考虑了误差源对方位角和井斜角的影响,测量工具通常根据一个标准偏差来反应测量精度,加权函数对每个工具都是唯一的,对于这一分析,测得的深度、井斜角和方位角的在一西格玛精度下的标准偏差分别为0.3 m、0.25°和0.36°(即σH=0.3,σI=0.25,σA=0.36),整口井的标准偏差为常量。图2为标准正太分布图。
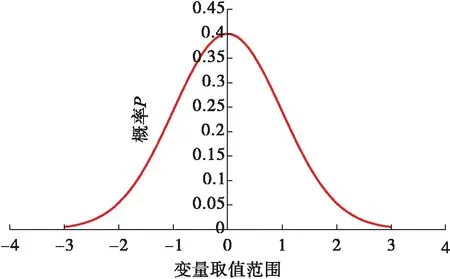
图2 标准正态分布
井眼轨迹空间位置用随机正态分布得到的测深、井斜角和方位角进行模拟即可得井眼轨迹不确定性范围散点图。

(4)

(5)
式中:I—井斜角,°;A—方位角,°。
3.三种井眼轨迹测斜计算方法的蒙特卡洛模拟结果
本研究是比较不同井眼轨迹测斜计算方法在假设分布条件下所产生的井眼位置不确定性,井眼轨迹测斜计算误差指的就是由某种测斜计算方法得到的井眼位置与真实井眼位置在相同测深处的井眼位置之间的距离。因此,首先需要定义真实井眼位置或者一个可以作为真实值的测量值。自动寻北高分辨率连续速率陀螺仪不受磁场干扰,而最小曲率法是目前井眼轨迹计算的行业标准,因此,根据陀螺测量数据用最小曲率法计算的井眼位置被认为是比较真实的井眼轨迹,可将其作为拟定真值[8]。
由于测点之间为曲线的假设相对来说更加符合井眼轨迹的实际情况,故本文选取中海油辽东湾某井的随钻测量和陀螺测量数据,就最小曲率法、曲率半径法和样条曲线法三种井眼轨迹计算方法展开了蒙特卡洛模拟分析研究。图3为三种方法的对比图。
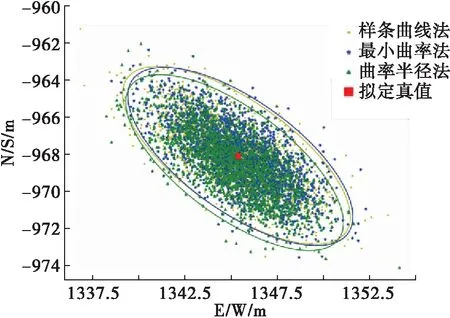
图3 三种方法井眼轨迹位置的蒙特卡洛模拟对比
二、三种井眼轨迹计算方法蒙特卡洛模拟统计对比分析
在上述计算实例中,样条曲线法较最小曲率法和曲率半径法在井眼轨迹不确定误差椭圆/球方面有了微小的变化。使用样条曲线法计算得到的井眼轨迹不确定误差椭圆/球的大小略大于最小曲率法和螺旋圆柱法,但是样条曲线法计算得到的不确定性误差椭圆/球的中心位置却更集中于拟定真值附近。若忽略置信区间的影响,则样条曲线法计算得到的井眼轨迹位置的不确定度因接近拟定真值而较最小曲率法和曲率半径法分别降低了约78%和91%。具体结果见表1和表2。

表1 蒙特卡洛模拟在井底测点的统计分析

表2 蒙特卡洛模拟在井底测点的不确定度分析
与1 m间隔的高分辨率测量得到的拟定真值相比,无论采用何种井眼轨迹计算方法得到的不确定度误差椭球都会在椭球中心处发生偏移。原因是系统误差未经过充分修正且测点之间的高狗腿度很难精确的去确定。图4是井眼坐标系下的井眼轨迹误差椭球各半轴的概率密度图。可以看出,30 m测量间隔计算的井眼轨迹误差椭球中心之间的差异显示了置信区间和概率密度之间的区别。

图4 井眼坐标系下井底测点误差椭球各半轴的概率密度图
三、结论与建议
(1)井眼轨迹测斜计算方法的蒙特卡罗模拟表明,各种井眼轨迹测斜计算方法在误差椭球不确定度表征上的差异不大是可以忽略不计的。忽略置信区间的影响,针对30 m的标准测量间隔距离,样条曲线法计算的井眼轨迹位置更准确,但与最小曲率法和曲率半径法一样受到系统误差的影响。
(2)计算井眼轨迹位置不确定度的大小不仅受各种误差因素(标准偏差)的影响,还取决于误差模型(本文为井眼轨迹测斜计算方法),蒙特卡洛计算机模拟简化了繁琐的计算过程,使得井眼轨迹测斜计算方法对比起来更加简单明了。
(3)针对最小曲率法计算的井眼轨迹,可以采取相应措施来大大提高测量的准确性,比如在滑动钻进之间的中点处进行测量或在已知的狗腿角较大的井段加密测量,这都将对井眼轨迹位置和井眼位置产生显著影响。
